基于自适应混沌PSO的三相PWM整流器PI参数优化整定
2020-11-06杨晓明毛安家
赵 琳,陈 贺,杨晓明,毛安家
(1.国网黑龙江省电力有限公司伊春供电公司,黑龙江 伊春 153000; 2.中国电力企业联合会,北京100761; 3.华北电力大学,北京102206)
0 引 言
三相PWM 整流器由于其结构简单、功率因数高和功率四象限流动的特点在电力电子领域得到了广泛的运用[1-2]。最常用的控制方法是采用PQ解耦控制,此控制方案具有控制结构较简单、动态响应快、控制精度高的特点,但是需要设置合理的PI参数[1-4]。PI参数整定是一项十分重要的工作,其参数的好坏直接影响到系统的性能[1]。传统的PI参数整定需要由初始参数值进行多次重复实验不断调试来选取最佳值[2],经验值调试是一个费时费力的过程,且通常只能取得相对意义上的最佳参数。
在知道三相PWM整流器的结构和参数后,可把PI参数的选取问题转换为一个优化问题,通过求解最优解来选取最优的PI参数,直接通过程序实现自动寻优过程,可以节省大量的时间和精力,甚至达到事半功倍的效果。
对于非线性优化问题,除少数具有特定属性的问题外,尚无成熟的数学求解方法。因此,在解决这类问题时,选用智能化寻优方法,如遗传算法、模拟退火算法、粒子群算法(Particle Swarm Optimization,PSO)、蚁群算法等,似乎已成为不二之选。在这类算法中,粒子群算法由于具有计算效率高、收敛速度快、程序易实现等特点,在优化问题中得到了普遍重视[5-6]。该方法最早是由美国电气工程师Eberhart和社会心理学家Kennedy在1955年基于鸟群觅食提出来的,经过多年的应用与发展,已经广泛应用于各工程领域。但是PSO算法也有其弊端,表现在前期收敛过快,容易早熟陷入局部最优解。针对这一问题,已经有很多研究人员提出了算法的改进措施,比如自适应权重、对群体的位置或者速度加入扰动等,都取得了较好的效果[6-7]。
针对基本PSO算法的不足,提出一种自适应混沌PSO算法,并将其应用到三相PWM整流器PI参数整定中。通过在Simulink中搭建三相PWM整流器,编写自适应混沌PSO算法Matlab程序调用Simulink模型来获取最佳的PI参数,最后将获得的PI参数和经验整定的PI参数的控制效果进行分析比较。
1 自适应混沌PSO算法
1.1 PSO算法
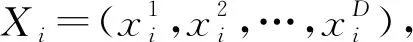
(1)
式中:i=1,2,…,m;d=1,2,…,D;ω为惯性因子;c1,c2为加速常数;r1,r2是[0,1]范围内的随机数;α为约束因子,控制速度的权重。
粒子群中的全部个体每进行一次迭代表示一次飞行,多次飞行后,就有可能产生群体最优解。
1.2 混沌扰动
混沌是自然界和社会中广泛存在的一种非线性现象,杂乱中包含规律,具有随机和遍历的特点,可在一定范围内不重复地遍历所有状态,混沌相对其他随机搜索更具优越性[7]。其中Logistic方程是一个典型的混沌,其方程为
Sk+1=μSk(1-Sk)
(2)
式中:k=0,1,2,…;μ为控制参量,μ∈ (0,4]。
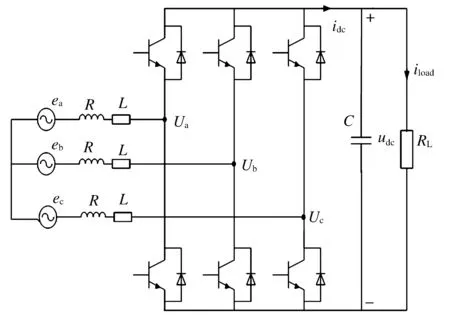
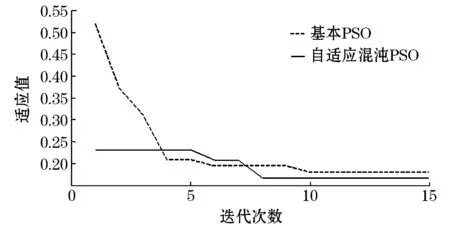
当μ=4,0 基本PSO算法主要存在以下几个缺点: 1)初始解群的选取是随机的,而初始解群的好坏将会直接影响到最优解的求取效率。 2)个体最优解和群体最优解在迭代中都是正反馈过程,由于搜索的精度问题,可能会收敛于局部的最优而不再变化。 3)惯性因子ω如果选取得太大,粒子可能在全局最优解中不断徘徊而无法取到最优解;ω如果选取得太小,粒子可能早熟而无法收敛到最优解。 针对上面问题,对基本PSO算法进行如下改进: 1)对于初始的粒子群,可以用不同的混沌初始值产生多个粒子群,从中选取一个最优的种群参与迭代。其中,对于每个初始的粒子群,对初始位置每一维变量随机选用一个初始值,该变量下的其他粒子值均由该初值经混沌方程迭代而成,具体如下式所示。 式中:rand()为一个[0,1]之间的随机值。 在产生多个初始粒子群后,选择适应最优的一个种群参与迭代。 2)为了防止种群陷入局部的最优解,可以在每次迭代后将粒子的位置进行小范围的混沌扰动,具体操作如下: ①混沌扰动操作产生扰动 ②扰动叠加 式中:h-为扰动的最大负偏差;h+为扰动的最大正偏差。h-与h+均可以根据实际进行选择。 3)为了防止惯性因子ω选取得太大或太小带来的影响,将惯性因子ω进行自适应处理,使其值随着迭代过程不断变小,使PSO算法可以在初期进行全局搜索,在后期进行精确搜索。 对约束因子进行线性化设置: ω=ωmax-(ωmax-ωmin)iter/iters 式中:ωmax和ωmin分别为最大惯性因子和最小惯性因子;iter为当前迭代次数;iters为粒子群总的迭代次数。 三相PWM整流器的拓扑结构如图1所示,网侧采用三相无中线连接,整流侧为三相桥式全控整流电路,IGBT和续流二极管并联作为各个桥臂开关器件[1]。 图1 三相PWM 整流器主电路结构 三相PWM整流器在dq旋转坐标系下的数学模型为[8] 三相PWM整流器控制器一般采用dq旋转坐标系下的PQ解耦控制[8]。将两相同步旋转坐标系d轴定向于定子电压矢量es的方向上,定子电压的d、q轴分量分别为 ed=e,eq=0 利用定子侧变换器dq旋转坐标系下的数学模型,可得输入电流与电压的关系如下: 式中:ud、uq为变换器交流侧电压的d、q轴分量,ud=Sdudc,uq=Squdc;Sd和Sq分别为开关函数在dq坐标系下的分量。d、q轴电流除受ud、uq的影响外,还受耦合项ωLids、ωLids和电网电压的影响。采用前馈解耦控制策略可以去除耦合项的影响[8],其控制框图如图2所示。 图2 PQ解耦控制框图 传统的PI整数整定需要在参数的初始值的基础上进行多次重复实验,并在其中选取最佳值,但受到实验次数限制,只能选取相对意义上的最优值。本文提出采用基于自适应混沌PSO算法,能在全局进行搜索,以确定系统的最优参数,对提高系统的性能具有重要的意义。 PI参数优化的目标是使直流侧的电压快速稳定在参考值附近,主要限制后期的误差,故采用直流输出电压偏差的ITAE(Integral of Time multiplied by the Absolute value of Error)指标作为自适应混沌PSO算法的适应度函数,其表达式为 式中:ts为响应时间;e(t)为在响应时间内直流侧给定电压和实际电压间的差值。因此,优化的目标函数为 min(fITAE) 0 0 0 0 式中:mi(i=1,2,3,4)为控制器参数的上限值。 混沌PSO算法的优化迭代步骤如下: 1)粒子群初始化。通过不同的混沌初值产生多个初始的粒子群,选择出最优适应度的种群,记录下该种群的群体最优解,并把个体的初始解作为个体最优解。 2)粒子群迭代。根据式(1)进行种群迭代,更新群体最优解和个体最优解。 3)粒子群中的位置扰动。采用Logistic混沌方程(2)产生混沌序列对种群的所有个体位置进行混沌扰动。 4)最大迭代次数判断。判断是否达到最大迭代次数,若达到精度要求则给出粒子群的最佳适应值对应的位置并结束程序,否则继续步骤2)直到达到最大迭代次数为止。 以某直流电动机稳压电源整流电路为算例,对三相PWM的PI最优选择问题进行说明。已知电网线电压380 V,电阻R=0.5 Ω,电感L= 11 mH,电容C=800 μF,直流电动机额定电压为660 V,额定功率P=5 kW,开关频率f=5 kHz,时间ts=0.5 s。对整流电路而言,相当于直流输出udc=660 V,直流负荷RL=87 Ω。采用Matlab/Simulink编写PSO算法和搭建三相PWM整流器模型,将PSO的参数每次传递给Simulink模块进行仿真,运行后读取直流侧的电压数据进行适应值计算以完成整个PSO算法,模型中所有控制参数的上限均取20。 作为对比,算例采取了3种方法整定PWM的PI参数:1)文献[2]推荐的经验值整定与调整法;2)基本PSO参数优化整定法;3)基于自适应混沌PSO参数优化整定法。各方法的基本步骤与计算结果如下: 1)经验值整定。Kup=0.01,Kui=1,Kip=1,Kii=10,调整步长分别设定为:ΔKup=±0.01,ΔKui=±0.5,ΔKip=±0.5,ΔKii=±1。调整过程中,如果相邻两次调整后目标函数值变化小于ε=0.01,则固定该值调整其他值,最终得到的整定参数为 Kup=0.07,Kui=5.5,Kip=5,Kii=30 2)基本PSO参数优化整定。设定粒子群的规模N=35,学习因子c1=c2=1,惯性因子ω=0.4,最大迭代次数iter=15,粒子数为35,经过10次迭代后适应值趋于不变,得到最佳的PI控制参数为 Kup=0.02,Kui=15.3,Kip=9.4,Kii=11.7 3)自适应混沌PSO参数优化整定。粒子群的规模设定为N=35,学习因子c1=c2=1,惯性因子ωmax=0.9、ωmin=0.1(随迭代次数增加而变小),最大迭代次数iter=15,初始产生的混沌种群个数为5,混沌扰动范围[-0.2,0.2],迭代7次以后适应值趋于不变,得到最佳的PI控制参数为 Kup=0.02,Kui=7.2,Kip=19.8,Kii=11.8 比较基本PSO算法和自适应混沌PSO算法的适应值收敛情况,如图3所示。 图3 迭代收敛曲线 由图3可见,自适应混沌PSO与基本PSO相比,由于初始的种群是在多个混沌种群中所选取出来的最优值,适应值的初值相对较小,并且后期的适应值也比基本PSO小,说明自适应混沌PSO找出了更佳的PI参数。 比较3种PI参数下直流侧电压跟踪调节效果,如图4所示。 分析不同PI参数的控制效果,由图4可见,3种方式在0.25 s左右时都可以将直流侧电压稳定在参考电压660 V 附近。但采用传统的基于经验整定的PI参数,电压在0.03 s时跌到了400 V左右,并在0.1 s左右重新达到660 V时存在较大的超调量;对于基本的PSO整定的PI参数,虽然不存在较大幅值的电压跌落,但电压超调量最大,系统调节时间最长;对于自适应混沌PSO,在达到跟踪电压660 V后,跌幅较小,超调量较小,系统也很快稳定在660 V附近。由此可见,自适应混沌PSO能得到更好PI参数的效果,对提升系统的性能有显著效果。 自适应混沌PSO所得的PI控制器的参数,相对于传统的经验整定以及基本PSO所得的PI参数,控制系统的直流侧电压无大幅度跌落,振荡小,能够很快稳定在系统的控制值附近。数值仿真验证了所采用方法的优越性,该方法显著减少了传统PI经验整定所需的时间和精力,具有事半功倍的效果。1.3 自适应混沌PSO算法
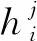
2 三相PWM整流器原理
2.1 三相PWM拓扑结构
2.2 dq旋转坐标下PQ解耦控制


3 基于自适应混沌PSO算法的PI参数优化
3.1 目标函数

3.2 混沌PSO 算法的优化步骤
4 算例分析
5 结 语
