汽车售后配件库存需求模型分析及应用
2020-11-06ZengRong
曾 荣 Zeng Rong
汽车售后配件库存需求模型分析及应用
曾 荣
Zeng Rong
(江汉大学 机电与建筑学院,湖北 武汉 430056)
为了提高汽车售后服务水平,实现配件库存需求的准确预测,采用灰色预测方法,首先对原始数据进行处理,其次通过灰色预测建立模型,最后对模型进行求解并检验,结果表明,原始数据处理后的预测结果更优。
配件库存;需求预测;灰色预测
0 引 言
库存管理是采购、生产与销售中的重要环节,是物流管理的核心,直接影响顾客满意度、存货积压风险等一系列问题。汽车售后配件库存管理是汽车物流管理中关键的一环,也是汽车制造、销售、保养和维修等环节的重要组成部分。科学合理的库存和保养汽车售后配件,能保持配件的使用价值,否则会使汽车配件质量下降,出现生锈、腐蚀等问题,使零件失去部分或者全部使用价值,带来巨大亏损;因此提高汽车配件需求量的预测精准度,有利于合理安排汽车配件库存[1]。
需求预测的方法主要分为2种,定性预测法和定量预测法[2]。定量预测法包括时间序列法和因果关系法,以及2种方法的组合[3]。时间序列法包括指数平滑法、移动平均法等。因果分析预测法包括回归分析法、灰色预测等方法,其中灰色预测方法的优点是不需要大量的样本,且样本不需要规律分布,计算工作量较小,可用于短期和中长期预测,其预测结果的准确度比较高。
1 预测模型选择
汽车售后配件的需求受众多因素的影响,如经济环境、技术水平、价格因素、配件历史维修情况等[4]。考虑到汽车售后配件需求的特点,选择灰色预测模型进行需求预测。
建立GM(1,1)(Grey Model,灰色模型)的具体步骤如下。
1.1 生成累加序列
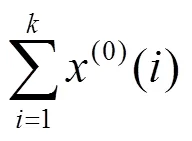
1.2 建立微分方程
对上述累加序列建立单变量微分方程
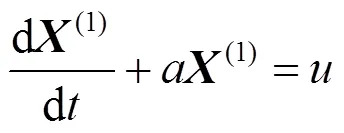
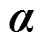
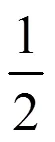
式(1)为式(2)的白化方程。
1.3 估计方程参数
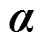
式中:=[(0)(2) ,(0)(3),...,(0)()]T;

(4)
1.4 求解模型拟合值
为了检验模型的拟合度,需要进行误差检验,判断灰色预测模型是否适合用于实际问题的预测。
1.5 检验模型精度
采用构造方差比和计算小误差概率的方法来检验灰色预测模型的准确性。计算方法为
(1)计算残差值;
(2)计算式(6)序列的方差1;
(3)计算原始序列(0)的方差2;
(4)计算方差比;
=1/2(7)
(5)计算平均相对误差;

(6)计算小误差概率。
(1-avg)Í100% (9)
指标和是后验差的两个重要指标。指标越小越好,当1越小、2越大时,越小。2值越大,表示原始数据序列方差大,原始数据离散程度大;1值越小,表明残差方差小,残差离散程度小。值小表明尽管原始数据很离散,但由模型所得的计算值与实际值之差并不过于离散。指标越大越好,表明预测值与原始值越接近,由两个指标可综合评定预测模型的精度。
参照表1可以对GM(1,1)模型精度进行具体评估,精度等级分为4级,1级精度最高,4级精度不被接受,见表1。

表1 精度等级
2 实例分析
汽车配件的销售情况直接影响库存,根据某汽车企业配件的销售数据预测其库存需求量。2008—2017年配件的实际销售数据见表2。
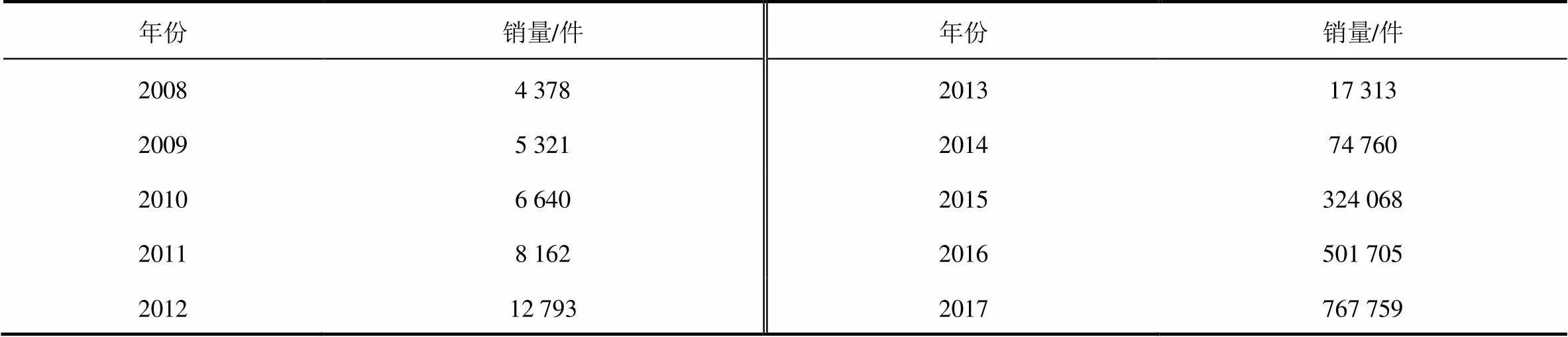
表2 2008—2017年配件销售数据
通过分析选取训练数据为2008—2014年数据,验证数据为2015—2017年数据,在MATLAB中运用最小二乘法拟合得到训练组的发展系数=1.154,灰色作用量=18 331.785,方差比=3.589 2、=0.091 2。对照表1可知该模型精度等级为4级,模型不可接受。
将原始数据进行取对数处理后,再次通过MATLAB计算,得到发展系数=0.063 402,灰色作用量=7.366 1,并得到方差比=0.196 5,小误差概率=0.960 1,对照表1可知该模型精度等级为1级,模型有效。采用此模型进行原始数据拟合,拟合度较好,并对后续年份的销量值进行预测,如图1所示。
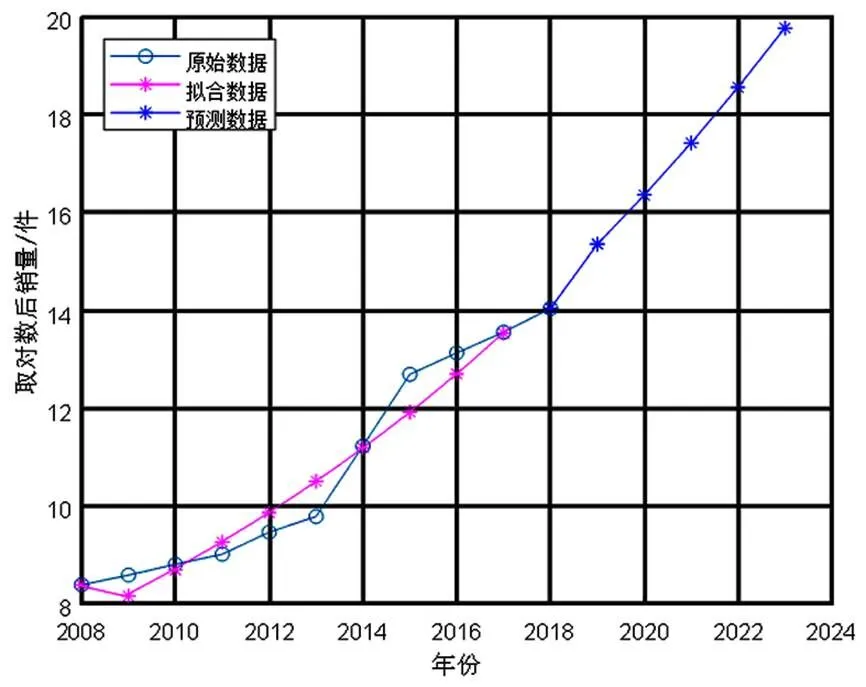
图1 取对数后的模型拟合度及预测结果
由图1可以看出,进行取对数处理后,数据的拟合度较好,预测精度提高。根据销售预测结果可初步预测出配件的库存需求量。
3 结 论
运用灰色预测法,通过分析原始数据,对原始数据处理后进行预测,实验结果比采用未经处理的原始数据预测结果更有效。由于汽车售后配件的需求受诸多因素的影响,如何更准确地预测其需求量将是下一阶段的研究方向。
[1]金淳,曹迪,王聪. 汽车零部件第三方物流仓储需求量集成预测模型[J]. 系统管理学报,2016,27(6):152-160.
[2]杨静雅,孙林夫. 基于QPSO-SVR的售后配件库存需求预测[J]. 计算机工程与设计,2015,36(9):2539-2543.
[3]闫娟. 灰色神经网络模型在物流需求预测中的研究[J]. 计算机仿真,2011,28(7):200-203.
[4]施卫海. 汽车零部件企业需求预测模型应用研究[D]. 上海:上海交通大学,2014.
2020-07-20
F253.4:U472
A
10.14175/j.issn.1002-4581.2020.05.013
1002-4581(2020)05-0052-03
