广东高职高考椭圆综合题的解题举例

文/佛山市顺德区李伟强职业技术学校 韦 生

广东省高职高考是招收中等职业学校毕业生的选拔性考试，数学科考试旨在测试考生对数学的基础知识、基本技能和基本的数学思想方法的掌握程度，对知识的认知要求分为了解、理解和掌握三个层次。近几年来，高职高考数学试题对椭圆知识的考查一般安排在第24题，是数学卷的压轴题，其中，第2小题学生得分率低、区分度高，因此，如何教学椭圆综合题，我们认为应注意以下问题。

一、正确理解概念定义，获取解题思路

2015年广东高职高考题第24题。

例1：已知中心在坐标原点，两焦点F1,F2在x轴上的椭圆E的离心率为4/5，抛物线y2=16x的焦点与F2重合.

(1)求椭圆E的方程;(2)若直线y=k(x+4)(k≠0)交椭圆E于C,D两点，试判断以坐标原点为圆心，周长等于△CF2D的圆O与椭圆E是否有交点？请说明理由.

(1)直线y=k(x+4)(k≠0)交椭圆E于C,D两点，包含以下事实：

隐含直线过椭圆的焦点F1，△CF2D周长等于=4a=20。

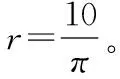
(3)判断圆与椭圆是否相交办法有两种。

由以上解题过程可知，正确理解题设条件，揭示条件蕴含的数学事实是成功解题的基础。

二、掌握基本技能，简化解题过程

2019年广东3+证书高职高考题第24题。

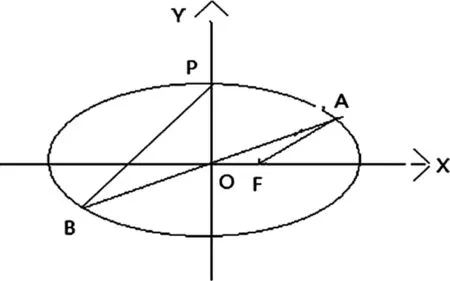
例2：已知椭圆的一个焦点为F(1,0)，且椭圆经过点P(0,1)，线段AB经过原点，A,B为椭圆上的点，且AF//PB.

(1)求椭圆的方程;(2)求三角形PAB的面积.

三角形PAB的面积怎么求？

首先，明确目标；

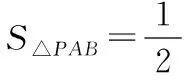
其次，选取解题方案：

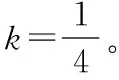
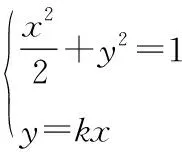
求出AB距离，点P到直线AB距离，求出面积。

方法2：由椭圆以原点为对称中心，上述解法改进为：

设点A(x,y),B(-x,-y),向量AF//向量PB，有y=x-1,又点A,B为椭圆上的点,

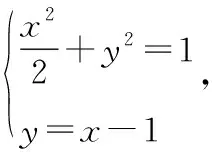
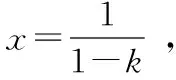
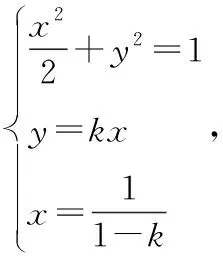
也可以挖掘题设，线段PB过椭圆的左焦点得出直线AB的斜率，求出三角形面积。

由上述几个解题方案看出，课堂教学要注意强化学生的解题信心，其次要使学生熟练掌握相应题型的解题基本思路和基本运算技能。比如，方法1解方程组有一定难度，学生如果没有强烈成功求解的欲望，就会容易放弃。方法2抓住椭圆为中心对称图形才能发现点A,B的坐标关系，才能够成功解题。方法3需熟悉直线上点的横纵坐标关系，才能够成功解题。

三、掌握基本题型解法，增多解题方案

2018年广东高职高考题第24题。

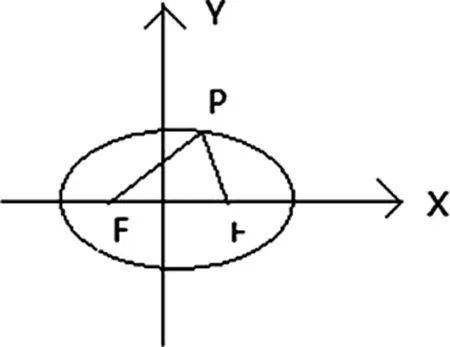
(1)求椭圆C的标准方程;(2)设点P为椭圆C上任意一点，求cos∠F1PF2的最小值.

与这类问题最有可能关联的方法是转化为二次函数求值或利用均值定理求解。

二次函数求法：

PF1+PF2=6,PF1=m,PF2=6-m

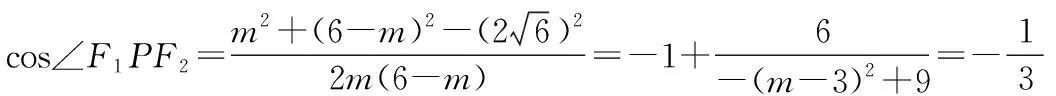
均值定理求法：

PF12+PF22=36-2PF1*PF2

当且仅当PF1=PF2=3时取等号，即最小值-1/3。

有些学生表示会写表达式但不会讨论。

方法1：由余弦定理，很容易书写出cos∠F1PF2表达式，引入字母表示：

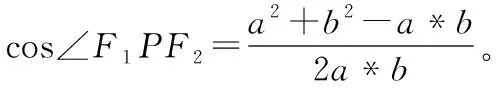
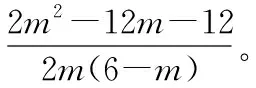
方法2需要熟悉均值定理，通过类比联想到a2+b2≥2ab,a+b=6,但也需要通过对分式进行化简求出答案。

在相应数学思想方法的指导下，熟练掌握基本题型解法基础，可通过类比找到解题思路，增加解题方案，提高解题能力。上面的例题都需要化简才能得出结论，因此教学应引导学生明确化简目的，讲清每一步的解题思路，才能接近解题目标，更好地培养学生的化简能力。

又如2013年广东高职高考题第23(2)题。在平面直角坐标系xOy中，直线x=1与圆x2+y2=9交于两点A和B，记以AB为直径的圆为C，以点F1(-3,0)和F2(3,0)为焦点，短半轴长为4的椭圆为D。(1)求圆C和椭圆D的方程。(2)证明：圆C的圆心与椭圆D上的任意一点的距离大于圆C的半径。

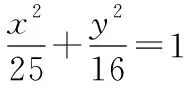
四、等价转化条件，简化解题过程

2017年广东高职高考题第24题。

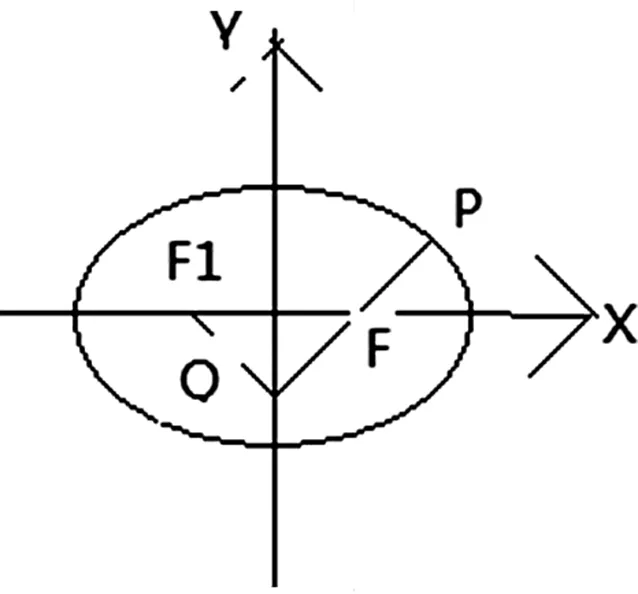
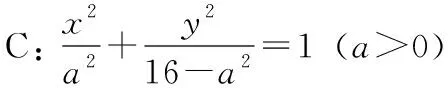
(1)求椭圆的方程；(2)设点P为第一象限位于椭圆C上的一点，过点P和F2的直线交Y轴于点Q，若QF1⊥QF2，求线段PQ的长．

常规解法：

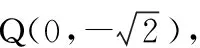
当解题思路受阻或运算过程过于繁杂，就应该回到题设，重新阅读题目或将问题转化、分解，结合解题目标，对条件、题设、相关定理、方法重新排列，获取成功解题信息。

比如，通过观察图形，分解问题，得出新的解法。

如果注意力集中在焦距F1F2与∠OF2Q=45°,注意力集中在点P在椭圆，会联想到椭圆的定义——PF1+PF2=6，进而合情合理地连接PF1,考虑三角形PF1F2,PF1+PF2=6,加之k=1,角PF2F1=135度，求PQ长变成求PF2+F2Q= PF2+2，从而得出新的解题方案：

在三角形PF1F2中，由余弦定理，设PF2=m,PF1=6-m,

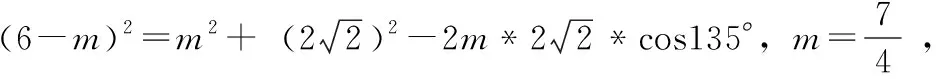
五、注意联想，获取解题思路

2016年广东高职高考题第24题。

(1)求椭圆C的方程；(2)求椭圆C上的点到直线L:y=x+4的距离的最小值和最大值.

“椭圆的参数方程”在中职教材作为选学内容安排，甚至没有安排这部分学习，用方法1求解对学生来说有难度,因此，需探索新的解题思路，可以通过以前做过的类似题目寻找解题方案。

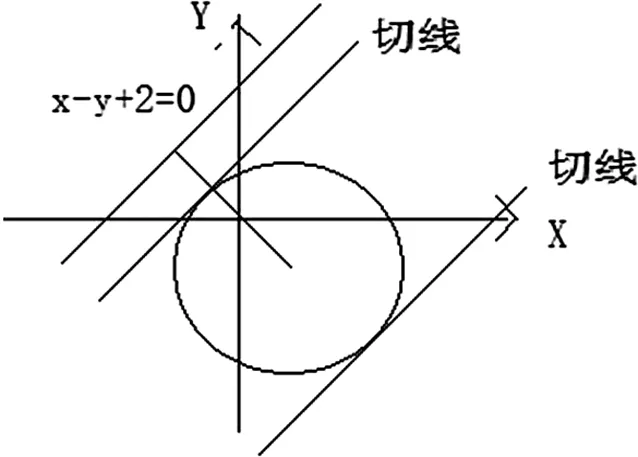
例6：求圆(x-4)2+(y+2)2=25上的点到直线x-y+2=0的最大距离和最小距离.

分析：圆心为(4,-2),圆心到直线x-y+2=0为d，数形结合知，圆上的点到直线最小距离为d-r,最大距离为d+r。

将上述方法直接运用，用原点替代圆心求出d，椭圆没有半径r,所以不存在d±r，由此探索新的解题方法：

数形结合，圆心到直线的距离与圆的交点应该是切点，如下图所示。将圆上的点到直线的距离转化为两条平行线间的距离问题。

设与直线x-y+2=0平行的直线为x-y+m=0

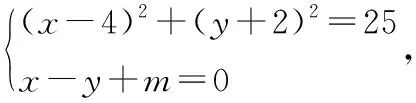
例5新的解法为：平行线距离。将问题背景转化为椭圆，即：

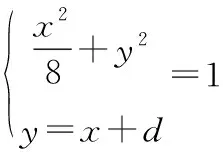
六、归纳总结，获取同类问题解题方法

通过改变问题条件，修正解题方法，获取一类问题的解法，提高学生分析解决问题的能力。

例7：

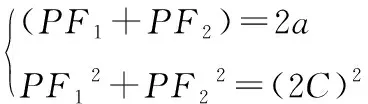
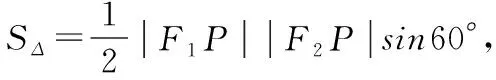
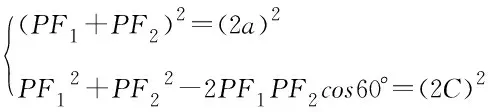
如果对题2条件改变，改为∠F1PF2=α，则得到更为普遍的结论。

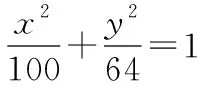
数学问题的解决离不开知识、技能技巧、数学方法的积累，对中职学生来说，既要加强对知识的正确理解与积累，又要加强对解题活动的总结。结合上述实例借助图形辅助的思路发现，体验解题活动就是“动员与组织、辨认与回忆、分离与组合”知识方法的提取过程，因此，需要总结如何才能顺利调动大脑已有的数学知识方法来解题，优化知识方法的“存储”，达到易于“提取”的目的，从而提高解题能力。