基于表面波增强效应的圆柱表面缺陷检测方法研究
2020-11-05徐志祥关守岩李连福
徐志祥,杨 帆,关守岩,李连福
(大连理工大学机械工程学院,辽宁 大连 116024)
1 引 言
金属圆柱作为主要的支撑传动类零件,其表面缺陷检测一直是检测领域重要的方向。在众多检测的方法中,激光超声无损检测能够实现非接触实时在线检测,且检测精度高,因此在检测领域受到了广泛的关注[1]。
许多研究学者将激光超声应用于微小缺陷的检测,并取得了多项研究成果[2-6]。陶程[7]通过有限元方法分析了声表面波与金属平板表面缺陷的作用机理,给出了能够定量表征表面缺陷的特征量。刘辉[8]通过数值仿真和实验验证了金属平板表面的反射瑞利波与表面缺陷深度之间存在时间依赖性。以上研究主要是将声表面波应用于平板类的表面缺陷检测,对于圆柱类表面缺陷检测还需要进一步的研究。
由于声表面波在圆柱表面传播会产生色散和相移现象[9-11],这与声表面波在平板上的传播规律不同,一定程度影响了检测表面缺陷的位置精度。针对上述问题,通过扫描检测点的方式,当表面波传播至表面缺陷前沿时,入射波和缺陷反射波产生叠加干涉会使缺陷前沿的表面波幅值出现显著增强的现象,刘学坤[12]通过实验已经验证了表面波增强效应。本文利用表面波增强效应确定圆柱表面缺陷的位置,分析表面波在缺陷附近的传播路径得到缺陷深度计算公式。通过分析比较,此方法能够有效提高检测圆柱表面缺陷的位置精度并能定量表征缺陷深度。
2 数值模型的建立
2.1 圆柱几何模型的建立
本文建立三维圆柱几何模型,如图1(a),激光以线光源加载在圆柱表面上,由于文中主要研究圆柱周向表面波和表面缺陷的作用,因此将三维模型简化为二维模型,如图1(b)。
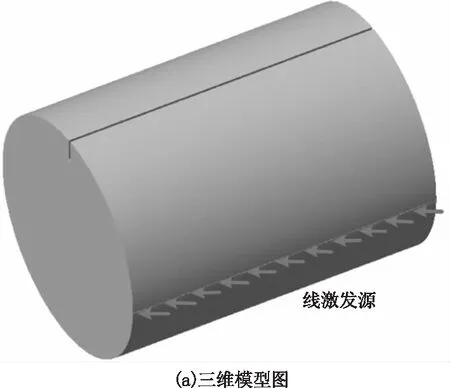
图中,θ为检测点与线源激发点之间的周向角度;η为缺陷与线源激发点之间的周向角度;圆柱直径为10 mm。
2.2 激光加载方式的选择
基于热弹性理论,文中通过有限元方法分析激光加载在圆柱表面产生超声波的过程。脉冲激光通过圆柱透镜汇聚成线激发源加载在圆柱表面,一部分激光能量被圆柱材料吸收,由于热传导作用会在激光加载区域形成温度梯度场,受热区域会产生热膨胀应力波在体内和圆柱表面传播。数值仿真模型中采用高斯热源模拟激光加载方式,其中热通量加载方程为:
Q(φ,t)=I0Rf(φ)g(t)
(1)
其中,I0表示高斯热源入射光斑中心处的最大功率密度;R为铝圆柱材料表面吸收率,值为0.06;f(φ)和g(t)分别为高斯热源在空间和时间能量分布方程,表示能量分别在极坐标角度方向上和时间轴上呈高斯分布。其中:
f(φ)=exp(-(rφ)/a02)
(2)
g(t)=t/t0exp(-t/t0)
(3)
式中,r为圆柱半径;a0为激光光斑半径;t0为脉冲激光的上升时间;φ为线源激光在圆弧上的辐照区域。
2.3 网格的划分和时间步长的选取
数值仿真实验中,激光激发能量E为1 mJ,激光激发半径a0为0.1 mm,脉冲激光上升时间t0为10 ns。为了满足激光作用后弹性波的传播精度要求和足够的空间和时间分辨率[13],根据公式:
(4)
Le=λmin/10
(5)
Δt=1/180fmax
(6)
选用自由三角形网格类型,在激光激发点和缺陷附近处网格大小为12 μm,其余网格大小为60 μm,时间步长为5 ns。数值仿真模型中选用铝圆柱材料物性参数如表1。

表1 铝的材料属性
3 表面波在周向圆柱表面的传播规律
3.1 圆柱周向表面波的频散现象
由于激光激发的声表面波频带较宽,不同频率的声表面波在圆柱表面的传播速率差异性较大,即会出现频散现象,影响表面波频散的因素主要有表面波的频率和圆弧表面的曲率半径。在圆弧表面上,表面波的低频分量传播速率大,高频分量传播速率小。在曲率半径为5 mm的无缺陷圆柱表面上,距离激发点120°检测点的时域图如图2(a),图中可以看到表面波中的低频分量和高频分量会出现分离。表面波的频散情况可以用表面波速度c和Rayleigh波速度CR的比值表示,比值与1差值的绝对值越大,表面波在圆柱表面的频散越明显[11]。文献[14]中给出材料铝中CR的速度约为2810 m/s,为了分析表面波在圆弧表面传播的频散情况,图2(b)是曲率半径分别为3 mm、5 mm、8 mm的圆柱表面距离激发点90°位置的时域图。通过脉冲反射回波方法计算得到分别为CR分别为2847 m/s、2825 m/s、2817 m/s。可以看出曲率半径较小时表面被速度和CR差异较大,频散较为明显,随着曲率半径的增大频散现象有所减弱,当曲率半径趋于无穷时,即为平面状态时,几何频散现象消失。
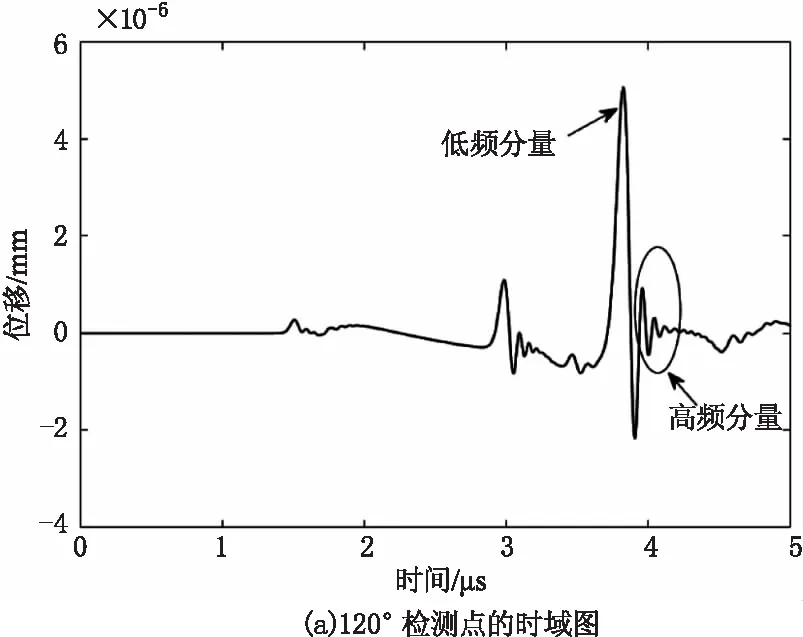
3.2 圆柱周向表面波的相移现象
文献[11]表明表面波在圆弧凸起外表面会发生相移,图3是表面波在曲率半径为5 mm的圆弧表面上不同角度检测点的相位。从图中可以看到,不同的检测点的相位不同,且圆弧表面相移现象相对于频散更加明显。图4是表面波在曲率半径为5 mm圆柱上距离激发点不同检测角度得到的时域图,图中不同角度检测点的曲线极性发生了变化[15],在30°到90°之间由双极性逐渐转化为单极性,90°之后又逐渐转化成为双极性,因此通过分析不同检测点的极性变化趋势,选择出现单极性波的角度作为信号检测点的位置能够提高信号的信噪比。

图3 不同角度检测点的相位变化

图4 不同角度检测点的极性变化
4 圆柱表面缺陷的检测方法
4.1 脉冲回波法
圆柱表面确定缺陷是通过计算表面入射波和反射波的时间差确定表面缺陷距离检测点的位置,计算缺陷底端表面反射回波和缺陷顶端散射回波之间的时间差确定缺陷深度。文中建立半径为5 mm圆柱模型,为了更好的实现入射波和反射波分离,表面缺陷位置在圆柱表面与激发点周向相距90°,检测点位于激发点与缺陷之间,与激发点周向相距45°,缺陷深度为1 mm,缺陷宽度为0.1 mm。在检测点45°得到的时域图如图5所示。
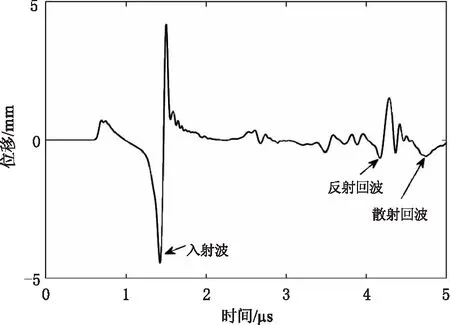
图5 45°检测点时域图
4.2 扫描检测点法
由于表面波在圆柱表面传播会发生频散,检测点接收到反射回波成分较为复杂,对于脉冲回波法确定缺陷的位置和深度会受到一定的影响。文中采用扫描检测点的方式,当扫描到缺陷前沿时入射波和反射波会产生叠加干涉现象,幅值明显增大,有利于确定缺陷位置。图6为扫描到不同角度的波形图,图中可以看出当检测点接近缺陷前沿时,幅值显著增大,扫掠过缺陷后,幅值急剧减小,因此可以通过幅值突变位置确定缺陷位置。图7是缺陷距离激发点90°时圆柱上表面的B扫图,图中可以明显看到在90°附近会出现反射纵波和反射表面波,并且能观察到入射表面波在90°附近的幅值增大的现象。

图6 缺陷附近检测点的时域图
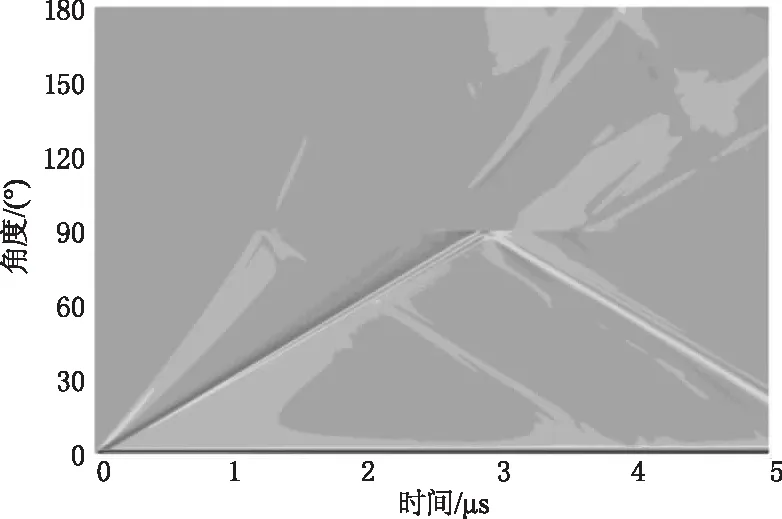
图7 带缺陷圆柱表面的B扫图
由于缺陷宽度为0.1 mm,因此缺陷前沿在89.43°附近处。图8分别为有缺陷和无缺陷89°检测点的波形图,在有缺陷波形图中的2.79 μs和3.49 μs出现了两个表面波,经过仿真实验分析,第一个表面波为入射表面波和缺陷反射表面波产生叠加干涉的复合波,其幅值显著大于无缺陷时的直达表面波幅值,第二个表面波是缺陷顶端散射波沿缺陷前沿传播至检测点的表面波。
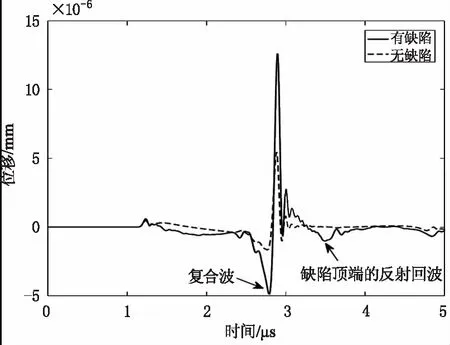
图8 89°检测点在表面有缺陷和无缺陷的时域图
因此表面波沿缺陷前沿往返传播的时间差就是两个波谷相距的时间,通过表面波的速度和两波谷之间的时间差可以计算得到表面缺陷深度。
图9分别为入射表面波到达缺陷底端检测点、表面波沿缺陷前沿传播和缺陷前沿散射表面波传播到缺陷底端检测点三个不同时刻的全场波形图。
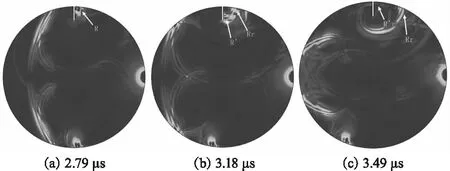
图9 不同时刻全场波形图
5 数值仿真结果分析
5.1 圆柱表面缺陷位置的确定
由于频散和相移现象,在圆柱表面通过脉冲回波法确定圆柱表面缺陷位置相对于平面,其位置精度会有所下降。本文基于检测点在缺陷前沿处出现的表面波增强效应,利用扫描检测点的方式确定缺陷的位置信息,一定程度上能减小频散和相移的影响。通过脉冲回波方法确定缺陷位置的公式为s=c1×Δt1/2,其中s为检测点与缺陷前沿的距离,c1为表面波的传播速度,Δt1为入射波和缺陷底端反射波之间的时间差,通过公式计算得到表面缺陷的位置误差为1.16°。如图6所示,通过扫描检测点方式确定表面缺陷的位置误差小于0.5°。因此通过扫描检测点的方式有利于提高确定圆柱表面缺陷的位置精度。
5.2 圆柱表面缺陷深度的确定
时间飞行散射法(TOFD)通过缺陷低端的反射回波和缺陷顶端散射回波之间的时间差和表面波传播速度确定缺陷深度。当检测点位于缺陷和激发点之间时,各类型反射波和转换波成分较多,得到检测点的波形较复杂,不易分辨出缺陷前沿顶端的散射回波。通过扫描检测点方式确定缺陷位置后,得到缺陷前沿检测点的波形如图8中有缺陷的波形图。
图中可以计算得到复合波和缺陷顶端散射回波的时间差和缺陷前沿的表面波速度,由缺陷深度计算公式h=c2×Δt2/2可以得到表面缺陷深度,其中h为缺陷深度、c2为缺陷前沿的表面波速度、Δt2为复合波和缺陷顶端散射回波的时间差。图10为表面波在缺陷附近的传播路径图,入射表面波R沿路径1传播至缺陷前沿底端,一部分在缺陷底端形成反射回波Rr沿路径2传播,另一部分表面波R′沿路径3在缺陷前沿传播,表面波R′传播至缺陷前沿顶端时发生散射,散射回波R′r沿路径4传回缺陷前沿底端的检测点,另一部分散射波透过缺陷,沿路径5、6、7传播。

图10 缺陷附近表面波的传播路径
为了验证图10缺陷附近表面传播路径和缺陷深度计算公式的有效性。分析在不同缺陷深度下,通过缺陷深度计算公式得到的仿真缺陷深度与实际缺陷深度的误差。图11是在不同缺陷深度下,缺陷前沿检测点的时域特征。

图11 缺陷前沿检测点在不同缺陷深度的时域特征
将缺陷深度在1.0~2.0 mm范围内的数值仿真结果经缺陷深度计算公式计算得到仿真缺陷深度与实际缺陷深度的关系如图12所示。

图12 仿真缺陷深度与实际缺陷深度之间的关系
由图12计算得到仿真缺陷深度与实际缺陷深度的误差如表2。表2中可以看出缺陷深度在1.0~2.0 mm范围内,仿真计算结果得到的误差百分比控制在6 %以内。表明了当检测点扫描至缺陷前沿时,利用表面波增强效应检测圆柱表面缺陷的可行性。同时也验证了图10表面波在缺陷附近的传播路径图和缺陷深度计算公式的有效性。

表2 仿真缺陷深度与实际缺陷深度的误差
6 结 论
本文探究表面波在圆柱周向表面的传播规律和与缺陷的作用方式,提出了一种基于表面波增强效应的圆柱表面缺陷检测方法。文中采用数值仿真的方法,通过扫描检测点的方式确定圆柱表面缺陷的位置和深度。研究表明:
(1)当检测点扫描至缺陷前沿时,入射表面波和缺陷前沿的反射表面波发生叠加干涉使检测点表面波幅值增加。通过表面波增强效应确定表面缺陷的位置,减小了表面波在圆柱表面传播的频散现象对表面缺陷的位置精度影响,提高了检测圆柱表面缺陷的位置精度。
(2)文中给出了基于表面波增强效应的缺陷深度检测方法。在缺陷深度范围为1~2 mm时,结合表面波在缺陷附近的传播路径和缺陷深度计算公式,计算得到数值仿真缺陷深度与实际缺陷深度的误差百分比控制在6 %以内,验证了该缺陷深度检测方法的有效性。该方法能够为定量表征圆柱表面缺陷深度提供了解决手段。
