软土地层大断面管幕箱涵顶进竖向姿态的理论与实测分析
2020-11-05杨忠勇廖少明刘孟波赵国强徐伟忠
杨忠勇,廖少明,*,刘孟波,赵国强,徐伟忠
(1.同济大学地下建筑与工程系,上海 200092;2.上海城建市政集团有限公司,上海 200065)
0 引言
管幕箱涵法是通过顶管机在箱涵顶进位置外围依次顶进单根顶管,管与管之间以锁扣相连,形成具有封闭性的管幕空间,而后在管幕的围护下顶进箱涵。该技术在上海北虹路下立交及田林路下穿中环线地道等工程中得到了成功应用[1-4],实践证明,该工法在保持开挖区域周围地层稳定性及控制地表沉降方面具有显著成效。
管幕施工与箱涵开挖顶进是管幕箱涵工法2个关键工序。何君佐等[5]结合田林路下穿中环线地道工程钢管幕群顶管姿态实测数据,分析研究了各类钢管在顶进过程中的相互作用以及管幕群贯通闭合后的姿态与变形规律;谢雄耀等[6]基于极限平衡法,采用理论模型揭示管幕作用下箱涵开挖面稳定机制对箱涵顶进过程中的开挖面支护等具有重要意义。
在管幕箱涵顶进过程中,箱涵机头的姿态与管节的姿态对工程有重要影响。若箱涵顶进姿态与设计轴线相差过大,轻则导致管幕结构变形进而影响周围地层稳定性并造成过大的地表变形,重则可能发生箱涵撞击管幕边缘等危险工况,导致箱涵顶进阻力剧增,无法正常顶进。因此,在箱涵顶进过程中,对其顶进姿态的监测与控制具有重要意义。
目前,对于非开挖技术的顶进姿态控制研究主要集中在盾构掘进与顶管顶进2方面[7-11]。王林涛[7]对盾构掘进姿态控制关键技术进行了深入研究,分析了盾构沿直线、圆弧曲线和缓和曲线3种典型隧道设计轴线掘进时盾构推进姿态变化规律,建立了根据盾构位姿求解各推进液压缸位移的数学模型,对盾构掘进姿态控制具有重要参考价值。胡景军等[10]、荣亮等[11]结合实际工程对矩形隧道顶管姿态控制技术进行总结,为同类工程提供了重要参考。
盾构掘进及箱涵顶进姿态控制方面的研究目前已有丰富的成果,但国内外学者在管幕箱涵顶进姿态控制方面却鲜有研究。与盾构及顶管相比,箱涵顶进的主要特点在于:1)箱涵断面尺寸大,顶进阻力大;2)顶推力作用在箱涵底部,偏离箱涵中轴线。箱涵顶进在体量及受力模式上与盾构、顶管具有显著差异,其顶进过程中的姿态变化具有相当的特异性,因此,盾构、顶管顶进姿态控制方面的研究成果无法直接在箱涵顶进中加以应用。基于此,本文通过理论分析揭示幕箱涵顶进过程中箱涵的受力特点及竖向姿态的变化特性,以期为同类工程提供指导。
1 工程背景
田林路下穿中环线地道采用管幕箱涵法,穿越长度86 m。暗埋段箱涵断面水平长度19.8 m,高度6.4 m,箱涵顶部埋深约7.0 m,见图1。管幕箱涵结构主要处于③淤泥质粉质黏土和④淤泥质黏土地层中(见图2)。地基土的主要物理力学性质指标见表1。
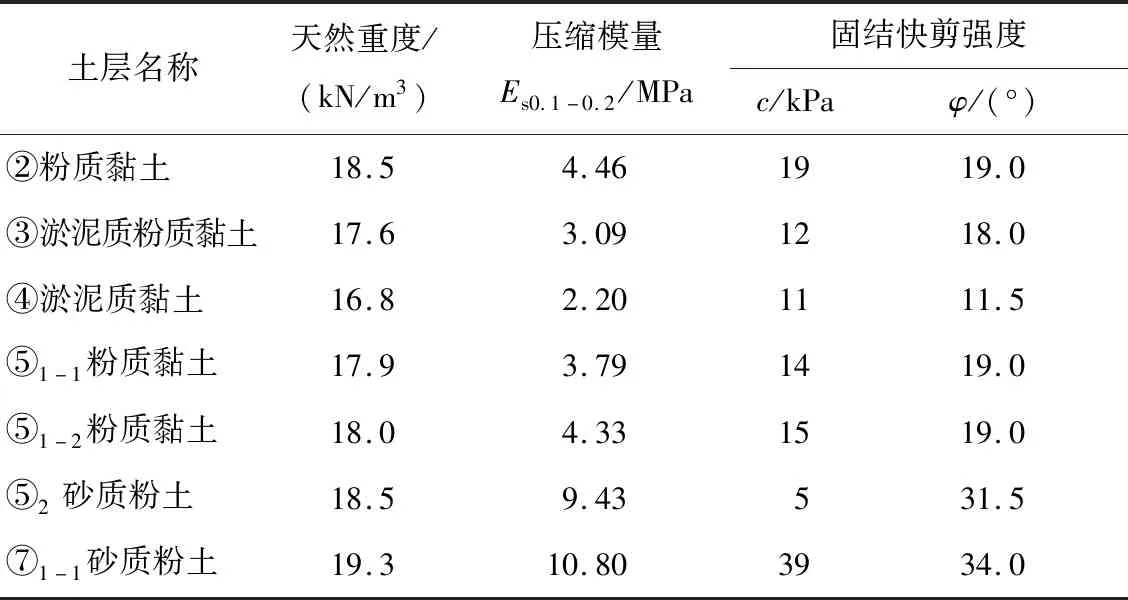
表1 地基土物理力学性质指标Table 1 Physico-mechanical properties of foundation soils

图1 工程下穿中环线暗埋段地道示意图Fig.1 Sketch of mined section of project crossing underneath Zhonghuan Line
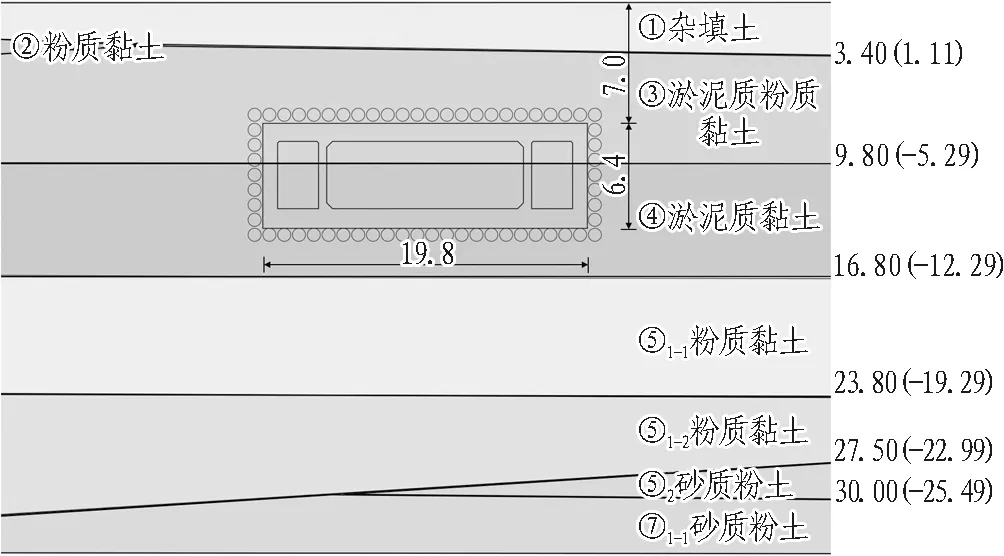
图2 箱涵断面图(单位:m)Fig.2 Cross-section of box culvert (unit:m)
箱涵顶进系统采用70只2 500 kN液压油缸千斤顶,分为7组,共175 000 kN,均设置在箱涵底部,见图3。

图3 箱涵底部千斤顶Fig.3 Jacks at bottom of box culvert
2 箱涵顶进"抬头"的力学机制分析
假定沿箱涵宽度方向受力均匀,可将箱涵"抬头"简化为二维平面问题,同时由于箱涵顶进是一个缓慢匀速顶进过程,可认为箱涵在这一过程中处于受力平衡状态。如图4所示,箱涵在水平方向上受到水平推力F1、迎面土压力e、正面附加反力rf以及管节和机头外壁的摩阻力f;在竖向上受到上覆土压力(pup+rup)、下覆土反力(pbot-rb)。假若顶推力与顶进阻力合力作用在同一轴线上,则箱涵只会因为开挖卸荷作用产生整体上浮,不产生偏转。但本工程仅在箱涵底部设置一排顶进千斤顶,顶推力作用轴线位于箱涵底部,而顶进阻力合力作用轴线位于箱涵中部偏下的位置(如图5所示),二者产生了管节上抬的力矩T,致使箱涵出现抬头。箱涵抬头会受到上覆土以及上排管幕的约束作用,这一过程中,箱涵上部压力增大、下部压力减小,由此产生了阻碍箱涵进一步抬头的抵抗力矩。当抬头量达到特定仰角θ时,箱涵结构重新达到平衡状态。
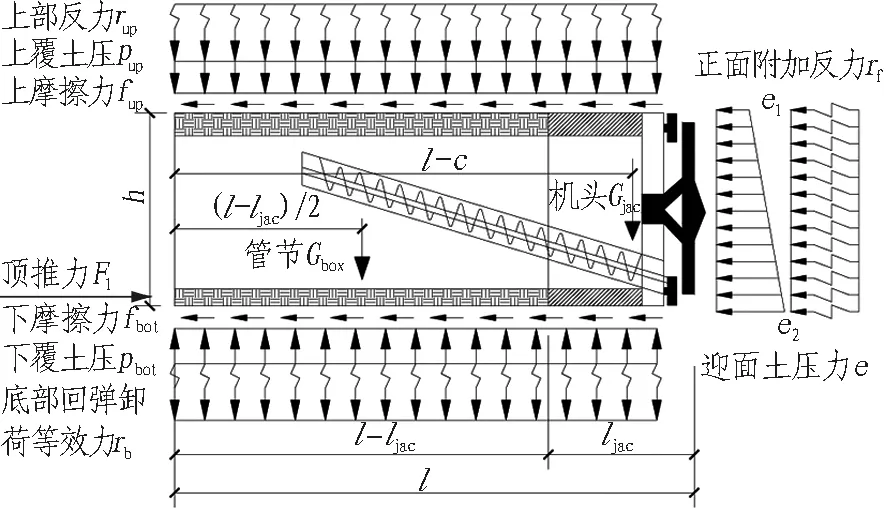
图4 首节箱涵顶进姿态简化分析Fig.4 Simplified analysis diagram of box culvert jacking attitude
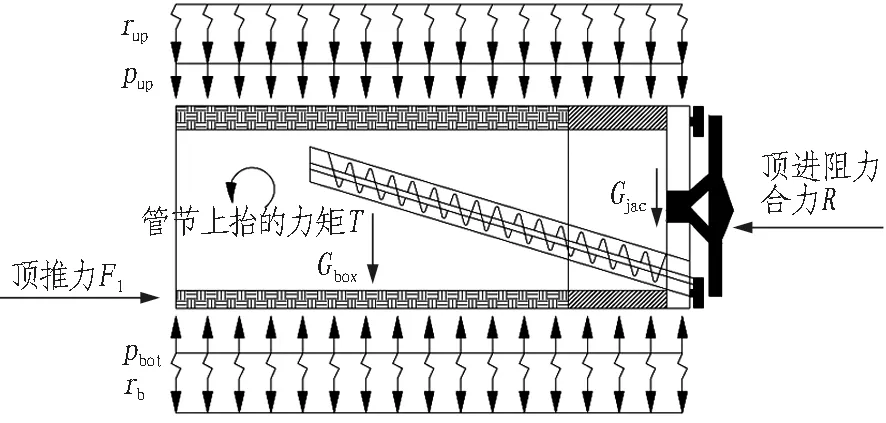
图5 首节箱涵"抬头"力学机制简图Fig.5 Mechanical diagram of lifting phenomenon of box culvert
3 刚接箱涵顶进的竖向姿态分析
3.1 总体方案设计
对于多节箱涵顶进,箱涵竖向姿态分析力学模型取决于箱涵管节之间的连接方式。如图6所示,若多节箱涵铰接,相邻箱涵管节之间会产生相对转动角,这对于小断面长距离顶进箱涵而言,有利于纠偏及轴线控制;但对于短距离超大断面而言,其灵敏度很低,为控制箱涵之间的接缝张开度及其旋转,箱涵间采用刚接。
综上,结合本工程实际,本文理论计算模型的基本假设如下:
1)箱涵与机头整体视为刚性体;
2)顶进过程缓慢匀速进行,箱涵处于静力平衡状态;
3)箱涵上下部介质(含管幕、地基土)采用Winkler局部弹性地基模拟。
(a) 多节箱涵铰接
3.2 箱涵竖向姿态的计算方法
假设箱涵顶进至掌子面距离始发位置l时,箱涵在始发位置产生了竖向位移Δz,并绕该位置产生了逆时针偏转角θ。此时,沿着隧道纵向,箱涵主要受力情况如图7所示。将图7中的分布力等效成集中力作用在分布力合力作用点,得到简化受力,见图8。考虑到θ为一小量,认为sinθ≈θ,cosθ≈1。
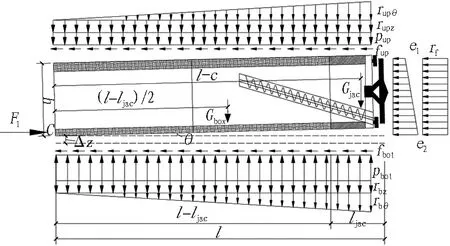
图7 箱涵管节及机头受力图Fig.7 Force diagram of box culvert and jacking head
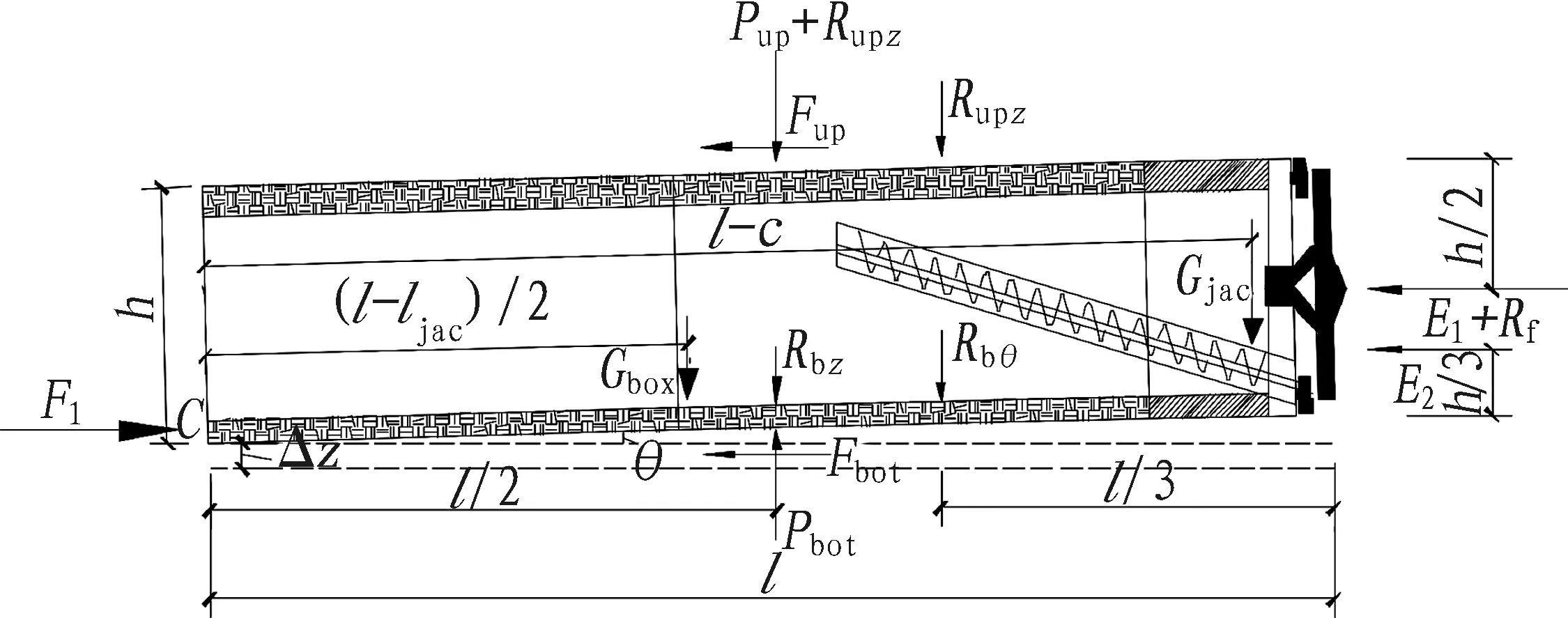
图8 箱涵管节及机头简化受力图Fig.8 Simplified force diagram of box culvert and jacking head
如图8所示,箱涵所受的力为上覆土重力Pup,箱涵自重Gbox,掘进机自重Gjac,底面初始反力Pbot,抵抗箱涵整体上浮的上部附加反力Rupz、下部等效卸荷力Rbz,抵抗箱涵转动的上部附加反力Rupθ、下部等效卸荷力Rbθ,顶推力F1,迎面土压力E1+E2,上下表面摩擦力Fup、Fbot,迎面附加反力Rf。根据箱涵受力平衡条件,即可求解得箱涵任一时刻的高程姿态。
箱涵水平方向受力平衡时,∑X=0。即
Pup+Rupz+Rupθ+Gbox+Gjac+Rbz+Rbθ-Pbot=0。
(1)
箱涵竖向受力平衡时,∑Z=0。即
F1-Fup-Fbot-E1-E2-Rf=0。
(2)
箱涵C点力矩平衡时,∑M=0。即
(Pup+Rupz+Rbz-Pbot)·l/2+(Rupθ+Rbθ)·2l/3+Gbox·(l-ljac)/2+Gjac·(l-c)-Fup·h-(E1+Rf)·h/2-E2·h/3=0。
(3)
式(1)-(3)中:Pup=γh0l,其中γ为上覆土平均重度,h0为箱涵埋深,l为箱涵顶进距离;Pbot=γ(h0+h)l,h为箱涵高度;Rupz=k1lΔz,k1为箱涵上部等效地基系数,Δz为箱涵整体上浮量;Rbz=k2lΔz,k2为箱涵下部等效地基系数;Rupθ=k1l2θ/2,为箱涵竖向偏转角;Rbθ=k2l2θ/2;F1=F/l,F为千斤顶组总顶力;E1=Kγh0h,E2=Kγh2/2,K为侧向土压力系数;Fup=μ1·(Pup+Rupz+Rupθ),μ1为箱涵上部摩阻力系数;Fbot=μ2·(Pbot-Rbz-Rbθ),μ2为箱涵下部摩阻力系数。
将式(2)E1+Rf=F1-Fup-Fbot-E2代入式(3),并联立式(1)得:
(3)
式中:a1=(k1+k2)l;b1=(k1+k2)l2/2;c1=γhl-Gbox-Gjac;a2=(k1+k2)l2/2-(μ1k1+μ2k2)lh/2;b2=(k1+k2)l3/3-(μ1k1+μ2k2)l2h/4;c2=γhl2/2+F1h/2+μ1γh0hl/2-Kγh3/12-μ2γ(h0+h)hl/2-Gbox(l-ljac)/2-Gjac(l-c)。
则按刚性体假设,箱涵头部竖向姿态(高程变化)为
z1=Δz+θ·(l-ljac)。
(4)
上述理论解析解适用于计算每个管节恰好完全进入土体时的箱涵竖向姿态,但由于箱涵姿态变化具有连续性,本文近似认为箱涵每节管在顶进过程中均符合上述模型。
3.3 箱涵顶进高程姿态与实测分析
根据田林路下穿中环线地道工程实际情况,理论计算模型中所涉及的主要参数取值如表2所示。
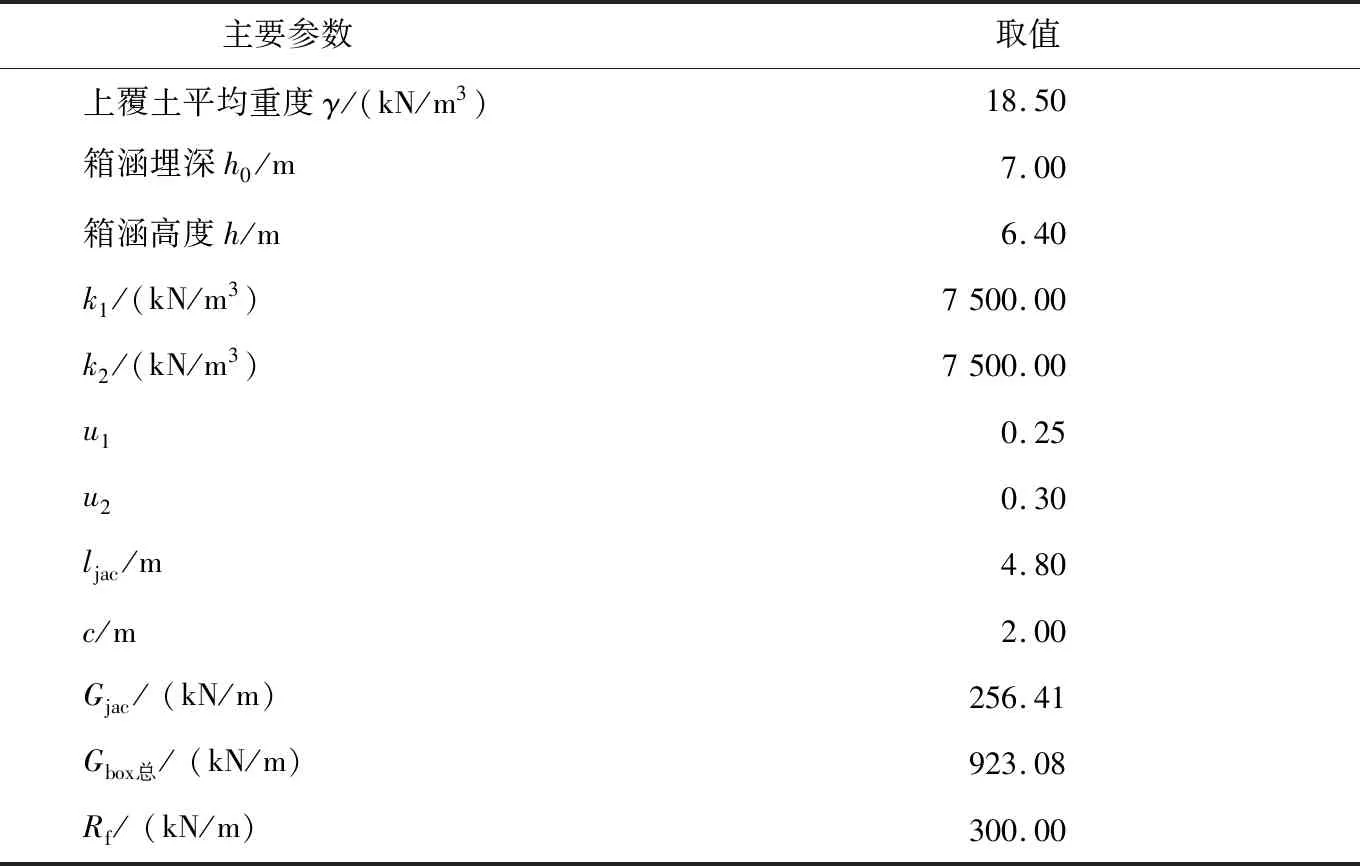
表2 主要参数取值Table 2 Main parameters
针对掘进机迎面土压力的应力状态,分别考虑以下3种工况。
工况1:掘进机迎面土压力按被动土压力考虑,即K=Kp=1.965,则F1=Fup+Fbot+E1+E2+Rf=[μ1γh0+μ2γ(h0+h)]l+Kpγh0h+Kpγh2/2+Rf=86.95l+2 249.40,kN/m。
工况2:掘进机迎面土压力按静止土压力考虑,即K=K0=0.674,则F1=Fup+Fbot+E1+E2+Rf=[μ1γh0+μ2γ(h0+h)]l+K0γh0h+K0γh2/2+Rf=86.95l+968.65,kN/m。
工况3:掘进机迎面土压力按主动土压力考虑,即K=Ka=0.509,则F1=Fup+Fbot+E1+E2+Rf=[μ1γh0+μ2γ(h0+h)]l+Kaγh0h+Kaγh2/2+Rf=86.95l+804.96,kN/m。
将上述3种工况对应的侧向土压力系数及千斤顶顶力值代入式(3),得到不同迎面土压力工况下箱涵高程姿态仰角随顶进距离的理论变化曲线,如图9所示。由理论计算可知,箱涵高程姿态仰角随着顶进距离的增大而迅速减小并趋近于0,且与千斤顶总顶进力呈正相关。具体地,以工况2(掘进机迎面土压力为静止土压力)为基准工况,当迎面土压力设定为被动土压力时,总顶力增加3.1×104kN,箱涵高程姿态仰角增加了51.9%~100.1%;当迎面土压力设定为主动土压力时,总顶力减小0.4×104kN,箱涵高程姿态仰角减小了6.9%~12.3%。
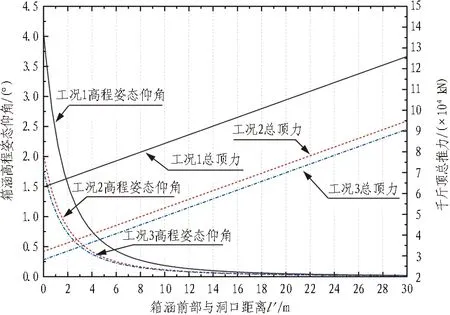
图9 不同工况下箱涵高程姿态仰角变化规律Fig.9 Curves of box culvert′s elevation angle under different conditions
箱涵顶进过程中,箱涵前部竖向位移实测变化曲线如图10所示。将箱涵顶进过程中箱涵前部竖向位移实测数据与不同工况下的理论计算值进行对比(见图11)可知,实测曲线与理论曲线的总体趋势大致相同。箱涵顶进前期,竖向位移以较快速度增长,后期达到峰值后逐渐减小并趋于平稳,并且前期实测竖向位移峰值介于工况1与工况2理论曲线峰值之间,其与实际施工中迎面土压力介于静止土压力与被动土压力之间相符,说明本文的计算结果具有较强的参考价值。
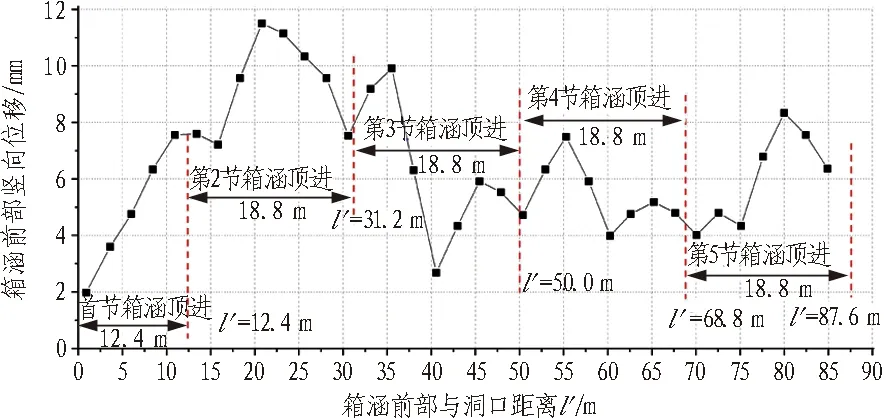
图10 箱涵前部竖向姿态实测变化曲线Fig.10 Curve of measured vertical displacement of box culvert
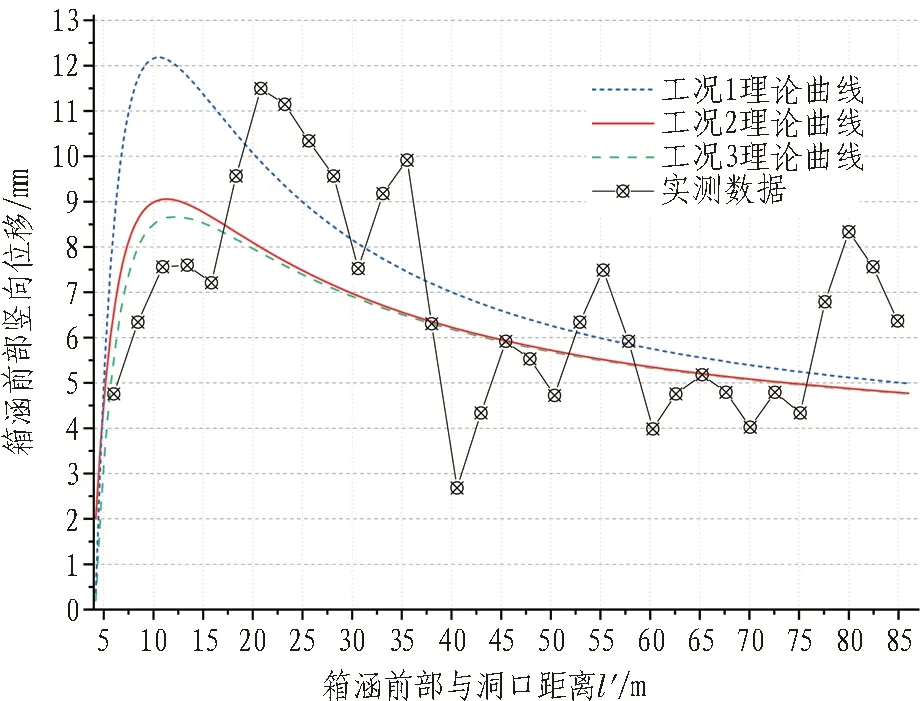
图11 箱涵前部竖向姿态理论与实测对比Fig.11 Comparison between theoretical and measured elevation attitude of box culvert
由上述分析可知,随着箱涵顶进距离的增大,箱涵高程姿态仰角迅速减小,箱涵前部竖向位移先以较快速度增长,达到峰值后逐渐减小并趋于稳定。箱涵顶进距离小于7 m时,箱涵高程仰角大,前部竖向位移增长快,该阶段是箱涵高程姿态控制的难点阶段,对于整个施工过程中的姿态控制尤为重要,需加强该阶段箱涵高程姿态的监测与控制。
3.4 箱涵竖向姿态主要影响因素分析
箱涵竖向姿态主要由始发和顶进2个阶段决定。其中,始发姿态包括竖向偏移和偏角。在不采取纠偏措施的情况下,箱涵始发姿态的竖向偏移将在后续顶进过程中得以继承,成为竖向位移附加常量;始发偏角则会导致箱涵前部竖向姿态附加值随着顶进距离线性递增。因此,箱涵始发姿态控制,尤其是始发角度控制,对箱涵竖向姿态具有显著影响。
对于箱涵顶进过程中的竖向姿态控制,由箱涵"抬头"机制分析可知,可以从减小由偏心顶推力与顶进阻力产生的使管节上抬的力矩、增大抵抗力矩2个角度采取控制措施以缓解箱涵抬头现象(如图12所示)。
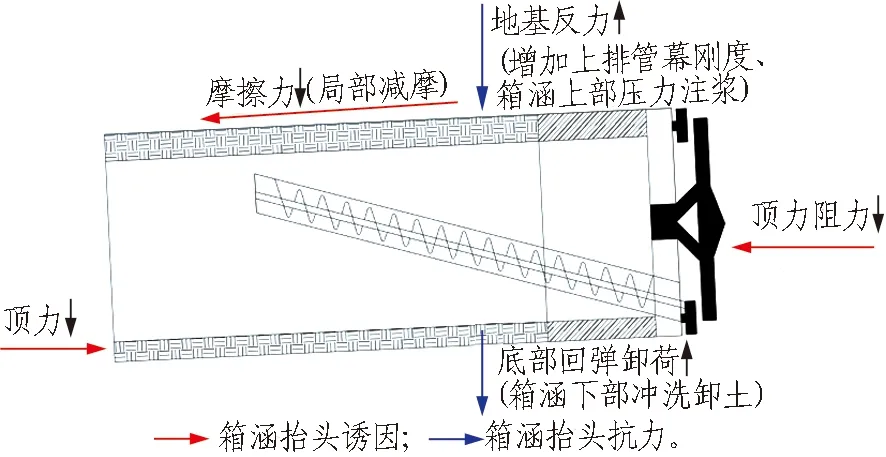
图12 箱涵抬头控制措施Fig.12 Control measure for lifting of box culvert
3.4.1 顶推力与摩擦阻力的影响
减少顶推力或掘进机迎面土压力、对箱涵上部进行局部减摩等施工措施均可以减小由偏心顶推力与顶进阻力产生的使管节上抬的力矩,从而减小箱涵竖向姿态偏转。具体地,由3.3节的数据分析中可知,相交于迎面土压力按被动土压力进行顶推力控制,按静止土压力进行顶推力控制对应的箱涵高程姿态仰角将减少34.2%~50.2%;箱涵上部局部减摩措施可以减小顶进过程中的迎面阻力,在理论计算中,可以采用减小箱涵上表面摩阻力系数μ1的方式模拟减摩措施的影响,图13与图14反映了不同程度减摩措施对箱涵高程姿态仰角的影响。箱涵上表面摩阻力系数μ1下降0.05,箱涵最大姿态角减小4.74%~5.24%。
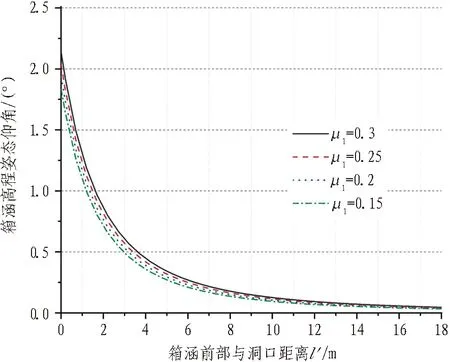
图13 减摩措施对箱涵高程姿态仰角的影响Fig.13 Effect of anti-friction measures on elevation angle of box culvert
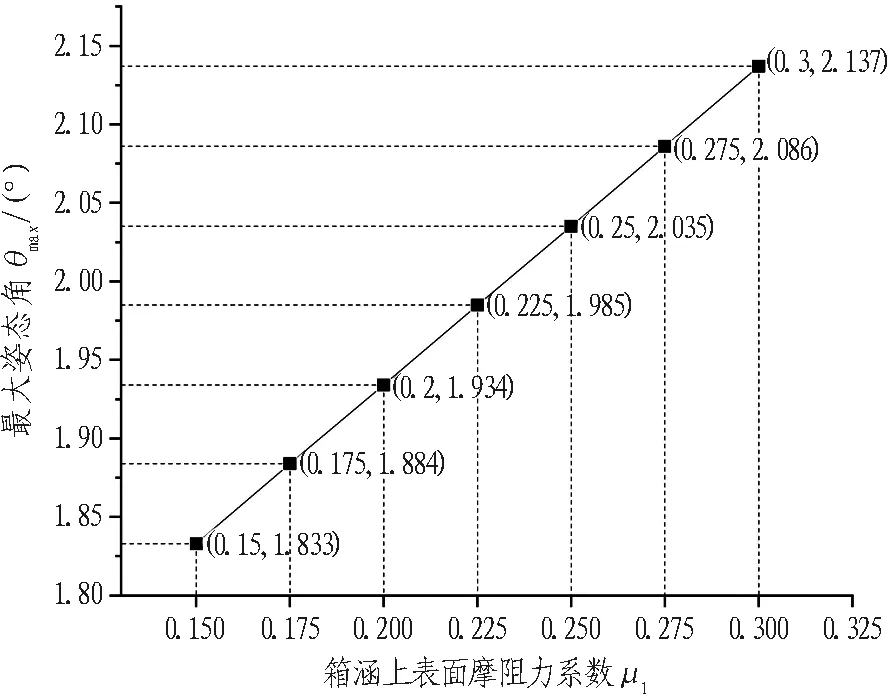
图14 μ1 -θmax曲线Fig.14 μ1-θmax curve
3.4.2 管幕刚度及竖向压力的影响
提高上排管幕刚度、箱涵上部压力注浆或配以箱涵底部冲洗卸土减少下部地基反力等措施可以增大抵抗力矩进而减小箱涵高程姿态偏转。具体地,在设计过程中,可以适当增大上排钢管幕的刚度(如增大管幕截面尺寸等)。在顶进施工过程中,可以采用通过箱涵顶板预留的注浆孔进行压力注浆,利用高压水流冲刷箱涵底部土体等措施。上述措施均可增大箱涵在"抬头"过程中所受阻力。在理论计算中,采用增大箱涵上部等效地基系数k1或箱涵下部等效地基系数k2的方式可以模拟上述措施的影响。由于在该理论模型中改变k1与改变k2无显著差异,故本节采用增大上、下部等效地基系数之和k1+k2(记为k)的方式模拟增大抵抗力矩系列措施的影响。图15与图16反映了增大抵抗力矩系列措施对箱涵高程姿态仰角的影响,箱涵上、下部等效地基系数之和k增加20%,箱涵最大姿态角减小15.67%~16.69%。
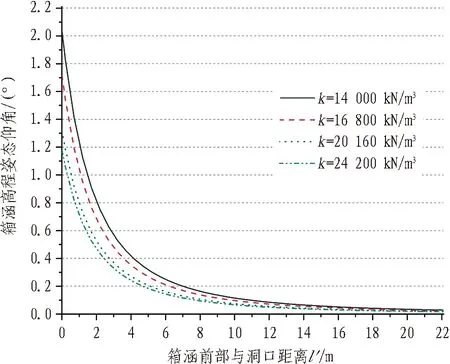
图15 抵抗力矩对箱涵高程姿态仰角的影响Fig.15 Effect of resistance torque on elevation angle of box culvert
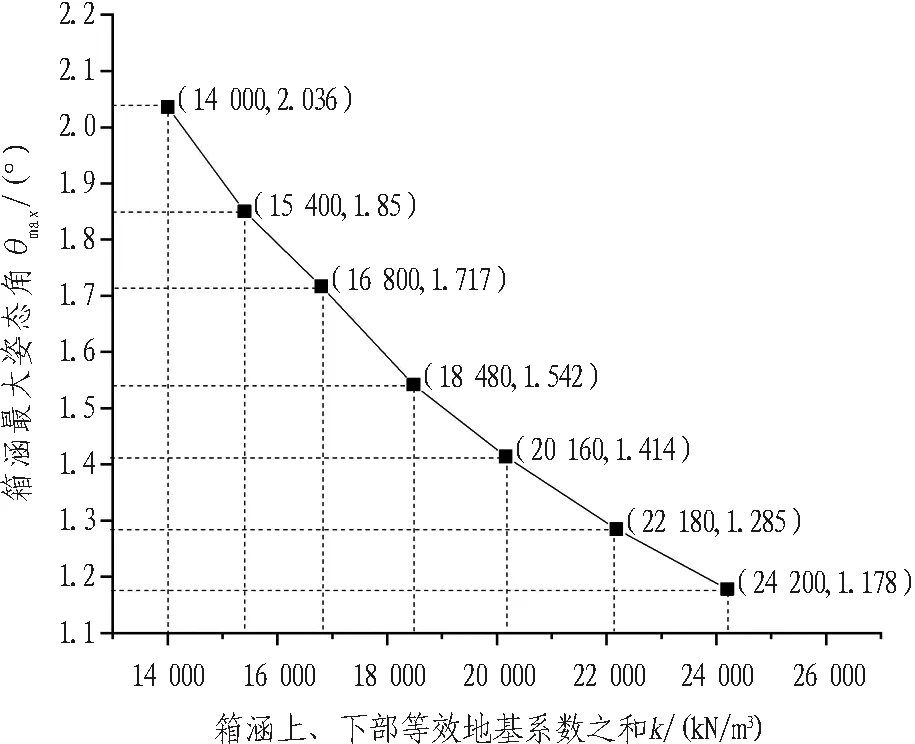
图16 k-θmax曲线Fig.16 k-θmax curve
4 结论与建议
本文基于局部弹性地基假定建立了软土地层超大断面管幕箱涵顶进姿态计算模型。通过理论计算和现场实测,对软土地层超大断面管幕箱涵首节箱涵顶进过程中的高程姿态变化规律和影响因素分析及研究,得到如下主要结论:
1)理论计算结果与实测吻合较好,表明理论计算模型能较好反映箱涵实际受力状态;
2)偏心顶推力与顶进阻力合力作用轴线不在同一高程而产生的使管节上抬的力矩是首节箱涵"抬头"的核心诱因;
3)首节箱涵顶进过程中,掘进机迎面土压力及千斤顶顶推力对箱涵高程姿态具有显著影响,相同条件下,与迎面土压力设定为被动土压力的工况相比,设定为静止土压力工况时顶推力减小3.1×104kN,箱涵高程姿态仰角减小了34.2%~50.2%;
4)箱涵上部局部减摩、增加上排管幕刚度等措施可以在一定程度上缓解箱涵"抬头"问题,但效果不及减小顶推力和掘进机迎面土压力明显,因此,在箱涵顶进过程中,通过配套调整推进速度、刀盘转速、刀盘贯入度等施工参数,适当降低千斤顶顶推力及掘进机迎面土压力应作为箱涵姿态的首要控制措施,其余施工措施可起辅助作用。
本文研究还存在一些不足之处以及可以进一步研究的地方。
1)本文针对管节间刚接的箱涵进行理论解析,未考虑相邻管节间的相对转角,后续研究可在本文提出的模型的基础上进行适当改进,对多节箱涵铰接的情况进行理论解析计算。
2)本文提出的箱涵竖向姿态计算模型是针对每个管节恰好完全进入土体时的受力状态建立的,在管节顶进过程中,忽略了未进入土体部分箱涵的影响,与箱涵的实际受力状态存在一定差异。
