漳河总干渠水流演进反演预测的神经网络模拟研究

艾学山，王永兵，陈祖梅，胡小梅

(1.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.湖北省漳河工程管理局，湖北 荆门 448156)

漳河灌区兴建于20世纪50～60年代，灌区总干渠首部连接漳河水库，中部挂接车桥、乌盆冲、杨家冲、东西库、烂泥冲水库，负责向二、三、四干渠灌区输水，涉及灌溉面积248.1万亩。漳河灌区是节水灌溉的示范区，在几十年的运行过程中，灌区坚持以提高灌溉水利用率和水分生产率为目标，通过体制机制改革、续建配套与节水改造及对灌区内各种工程设施的控制、调度与运用，在时间上和空间上合理分配水资源，在田间推行科学的灌溉制度与灌水方法，坚持计划用水、节约用水，推行计量收费，灌溉水有效利用效率大为提升，农业供水比重逐年降低[1]。目前，灌区的灌溉基本上以渠灌为主，如果可以提高输配水效率、缩短灌溉周期，使渠道蒸发渗漏和弃水减少到最低限度，便可实现低耗水，浇好地的目的。

在灌区实际背景下，下级用水户上报需水过程，再由上级管理单位统筹兼顾后制定出渠首下泄流量和放水时间。由于缺乏科学的水量与流量调节控制技术，调度人员往往凭借经验制定方案，造成了水资源的浪费，影响了农业用水的效率。如果可以根据渠道下游需水过程及其变化，反推出渠首下泄流量过程，将是灌区节约用水的又一潜力。为促进渠系更加科学合理地输配水，在给定各需水口分水过程的前提下，开展渠首放水过程的预测研究，对提升灌区渠系运行调度与管理水平具有重要意义。

1 人工神经网络简述

神经系统广泛存在于人和动物等生物体内，能够为生物提供外界环境识别、记忆、逻辑分析等功能[2]。1943年，美国心理学家McCulloch和数学家Pitts用逻辑学研究客观事件在形式神经网络中的描述，提出神经元的数学模型，称为MP模型，从而开创了对神经网络的理论研究。人工神经网络(Artificial Neural Networks，简写为ANNs)是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型，一般由输入层，隐藏层和输出层组成，每层可含多个神经元，输入层的神经元个数取决于输入数据，其他层中神经元的数目会根据实际情况进行调整[3]。

人工神经网络基本单元是含有激活函数的神经元，一个简单的人工神经元结构是一个多输入、单输出的非线性元件，其输入输出关系可描述为：

yi=f(Ii)

其中xj(j=1,2,…,n)是输入信号；θi是神经元单元的阈值；wji表示从输入信号j的权重；n为信号数目；yi为神经元输出；f(·)为传递函数，又称激发函数或激励函数。传递函数可为线性函数，0和1二值函数或S形函数。

这些神经元以一定方式联结，形成其网络体系的拓扑结构。通过对神经组织结构的模拟，从而具有类似于生物神经系统的某些特性，具有并行处理及自学习能力，且其鲁棒性也较好，因而应用广泛[4]。若传递函数为线性函数，则所建的神经网络称为线性神经网络。线性神经网络是最简单的一种神经元网络，可以由一个或多个线性神经元组成，其每个神经元的传递函数均为线性函数，因此其输出可以取任意值，线性神经网络可以采用Windrow-Hoff学习规则，即LMS(Least Mean Squre)算法来调整网络的权值和阈值，具有较好的收敛速度和精度，主要用于函数逼近、信号处理滤波、预测、模式识别和控制等方面。

1986年由Rumelhart，Hinton和Williams提出一种人工神经网络的误差反向传播训练算法(简称BP算法)，解决了多层网络中隐含单元连接权的学习问题。BP网络是一种单向传播的多层前向网络，网络除输入和输出节点外，还有一层或多层的隐含节点，同层节点中没有任何耦合。BP网络是目前应用最广泛的神经网络模型之一。在MATLAB的神经网络工具箱中，函数trainbpx( )采用动量法和学习速率自适应调整两种策略提高学习速度和算法的可靠性[5]。

2 数据选取

漳河灌区总干渠主要的监测断面和各分水口的拓扑关系如图1所示。

图1 总干渠主要的监测断面和各分水口的拓扑关系图

本文从漳河水库遥测数据库和人工记录表中选取资料系列相对较完整且能反映该时期主要流量的时段数据作为研究数据。选用了三组资料系列分别为：资料一，以2017年7月27日0点到8月10日12点共349个时段总干渠渠首闸流量，二干渠进水闸、三干渠进水闸、四干渠进水闸、总干渠一支渠1、总干渠二支渠的流量数据样本；资料二，以2019年1月13日0点到1月17日0点共97个时段的总干渠渠首闸流量、四干渠进口、三干渠进口的流量数据作为样本；资料三，以2020年2月17日0点到2月19日24点共72个时段的总干渠渠首闸流量、四干渠进口、三干渠进口和总干一支渠的流量数据作为样本；流量单位均为m3/s。

3 线性神经网络模拟

以MATLAB为工具，应用线性神经网络工具箱建立线性神经网络模型，以渠首闸的流量数据为输出，以其它分水口的流量过程数据为输入，进行线性神经网络模拟和训练。

3.1 选用资料一数据时

1)资料一共349个时段，按照渠首流量量级分多个数据段开展模拟研究。在60～70 m3/s流量时，首先选取前60组数据为训练数据，随后20组数据为验证数据，结果如图2所示。

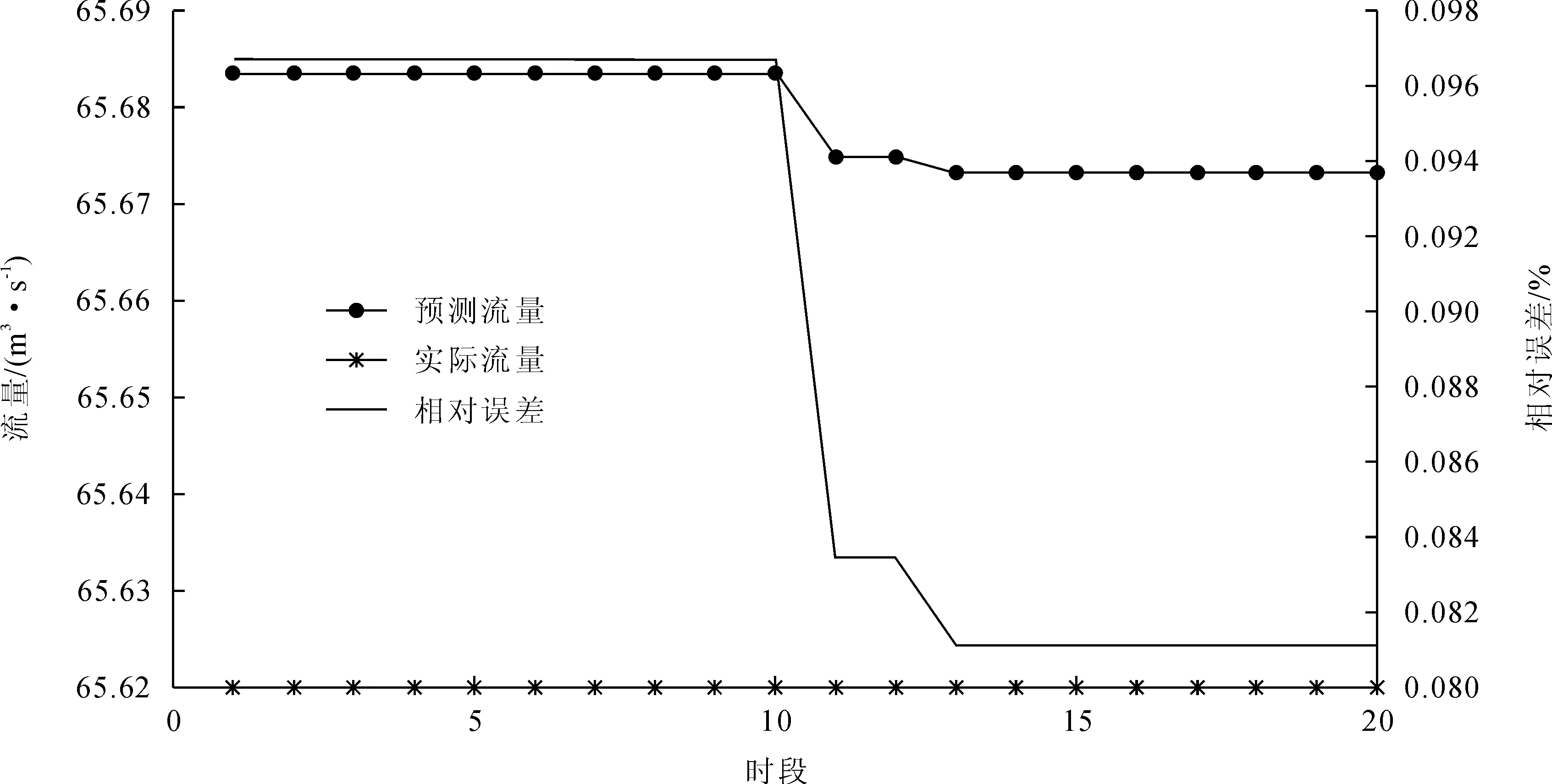
图2 资料一预测结果图1(60～70 m3/s流量)

2)在40～50 m3/s量级的流量时，选用100～150个时段为训练数据，151～175个时段为验证数据，结果如图3所示。

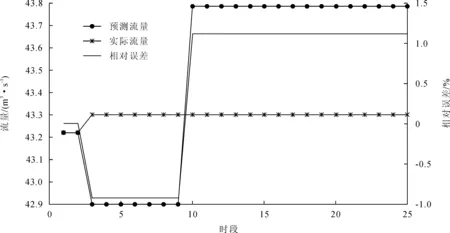
图3 资料一预测结果图2(40～50 m3/s流量)

3)在10～20 m3/s量级的流量时，以284～304时段为训练数据，以305～320时段为验证数据，结果如图4所示。

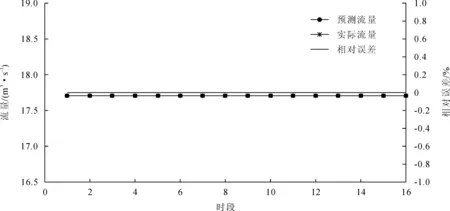
图4 资料一预测结果图3(10～20 m3/s流量)

3.2 选用资料二数据时

资料二共97个时段，流量数据变幅变小，将其作为统一资料系列研究。按照大致8∶2原则，即训练样本占80%，测试样本占20%的原则，下同，以前79个数据为训练样本，后18个数据为测试数据，得到结果如图5所示。

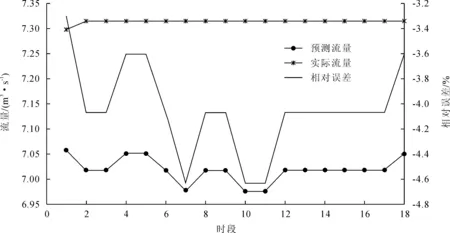
图5 资料二预测结果图(前79个训练，后18个预测)

3.3 选用资料三数据时

1)资料三级共72个时段，流量变幅也较小，按一个系列进行模拟，如以前60个时段数据为训练样本，后12个时段数据为测试数据，得到结果如图6所示。

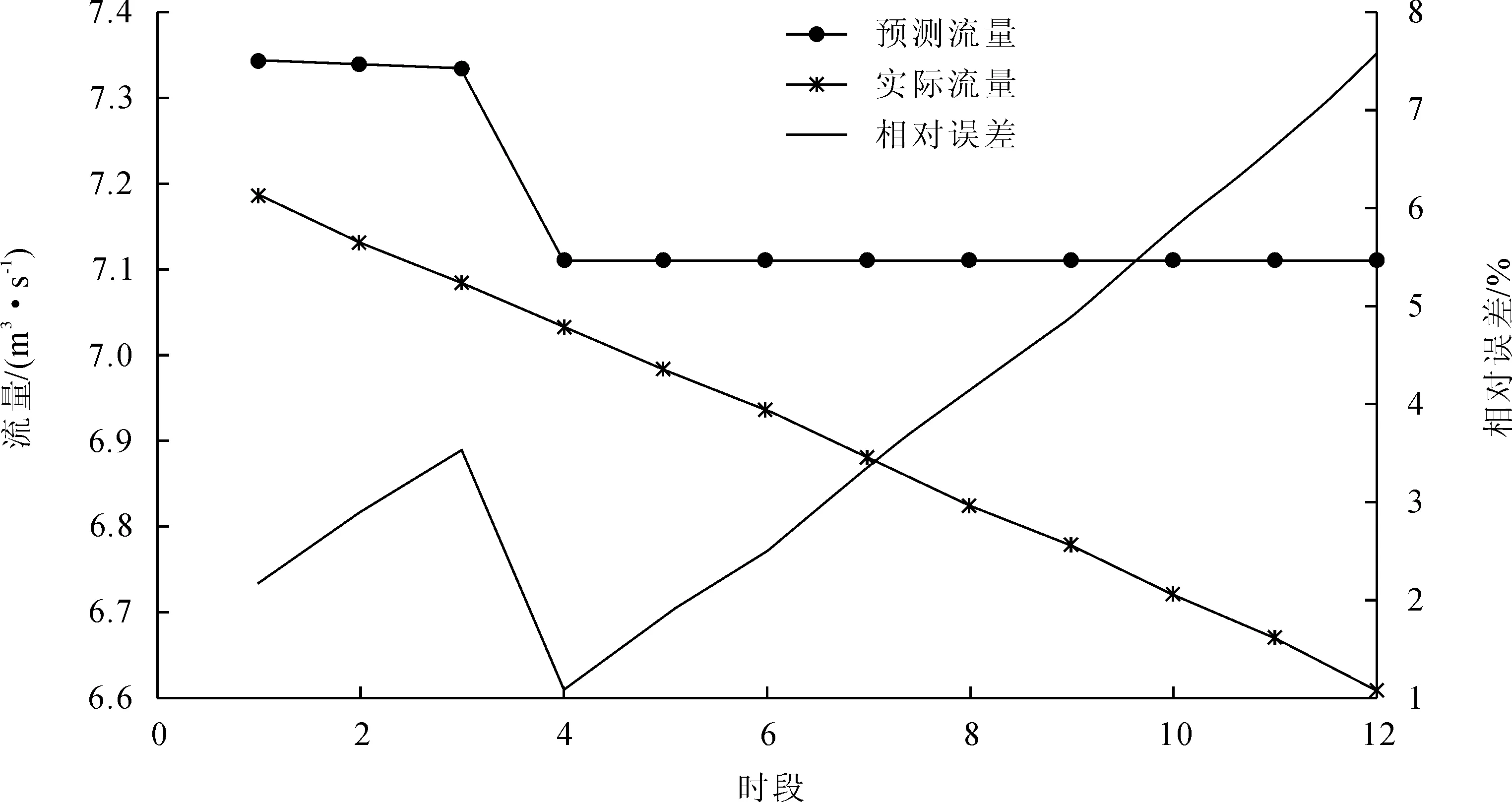
图6 资料三预测结果图1(前60个训练，后12个预测)

4 BP神经网络模拟计算

选用MATLAB神经网络工具箱进行程序开发，将各组数据分为训练数据和测试数据，将模拟结果与实际结果进行对比分析。

4.1 选用资料一数据时

资料一共349个时段，该资料系列渠首闸的流量先大后小，为使模型模拟更加精确，按渠首闸流量量级分为在50～70 m3/s流量级、30～40 m3/s流量级和10～20 m3/s流量级，并分别在各流量量级组内选取训练数据和验证数据，其中验证数据小于训练数据。此外，BP神经网络还可以将所有的资料作为训练数据，以其中部分时段作为验证数据进行研究。

1)50～70 m3/s流量级(共112组数据)。以前60组数据为训练样本，后20组数据为测试数据，得到结果如图7所示。

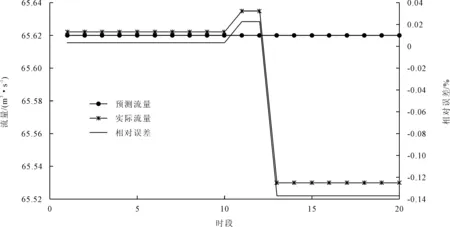
图7 BP网络资料一预测结果图1(60～70 m3/s流量级)

2)40～50 m3/s流量级(共76组数据)。以100～150个时段的数据为训练样本，151～175个时段的数据为测试数据，得到结果如图8所示。

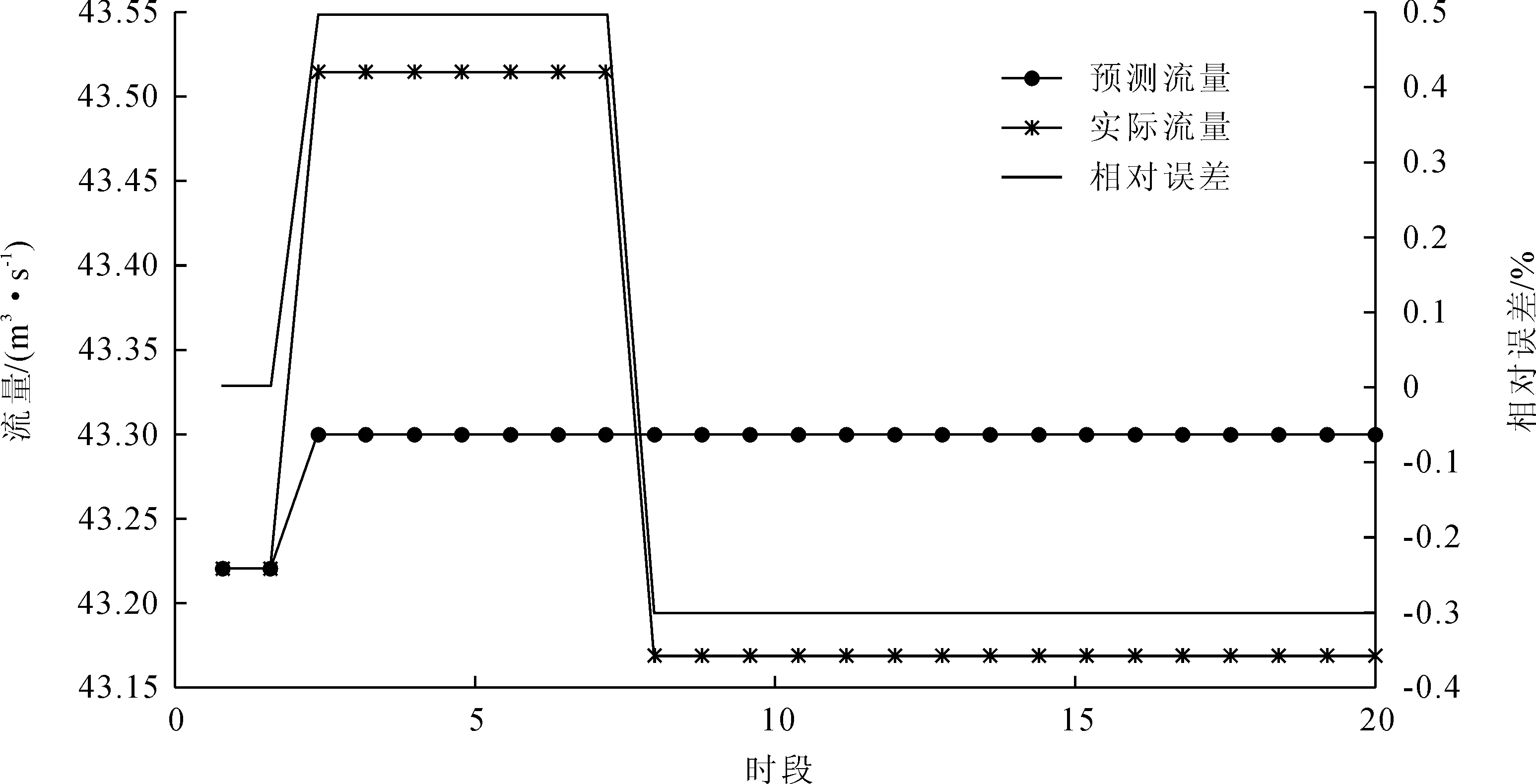
图8 BP网络资料一预测结果图2(40～50 m3/s流量级)

3)10～20 m3/s流量级(共35组数据)。以284～304时段为训练数据，以305～320时段为测试数据，结果如图9所示。

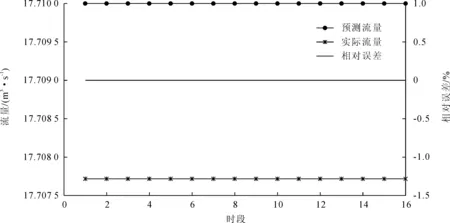
图9 BP网络资料一预测结果图3(10～20 m3/s流量级)

4)为充分利用现有资料，将全系列1～349时段所有数据为训练样本，以其中的部分数据段作为测试数据。如以106～179时段间数据作为测试数据时，结果如图10所示。

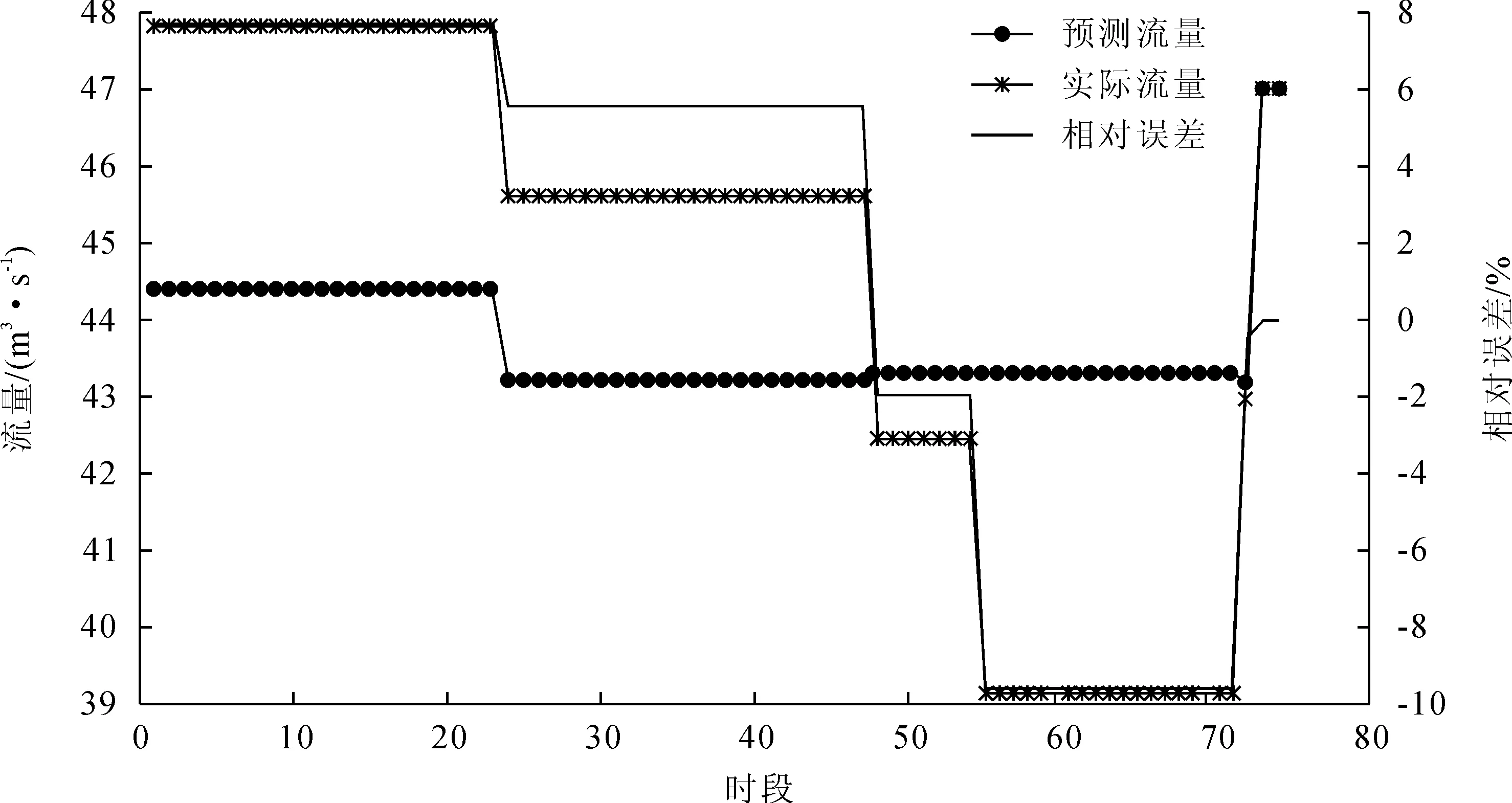
图10 BP网络资料一预测结果图5(所有数据训练，106～179组测试)

4.2 选用资料二数据时

资料二共97个时段，若以前79组数据为训练样本，后18组数据为测试数据，得到结果如图11所示。

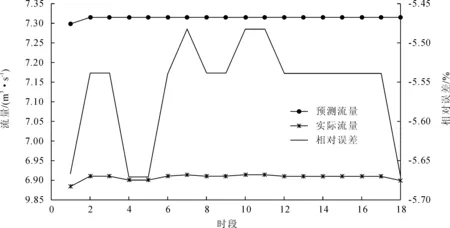
图11 资料二预测结果图(前79组训练，后18组测试)

4.3 选用资料三数据时

资料二共72个时段，若以前60组数据为训练样本，后12组数据为测试数据，得到结果如图12所示。

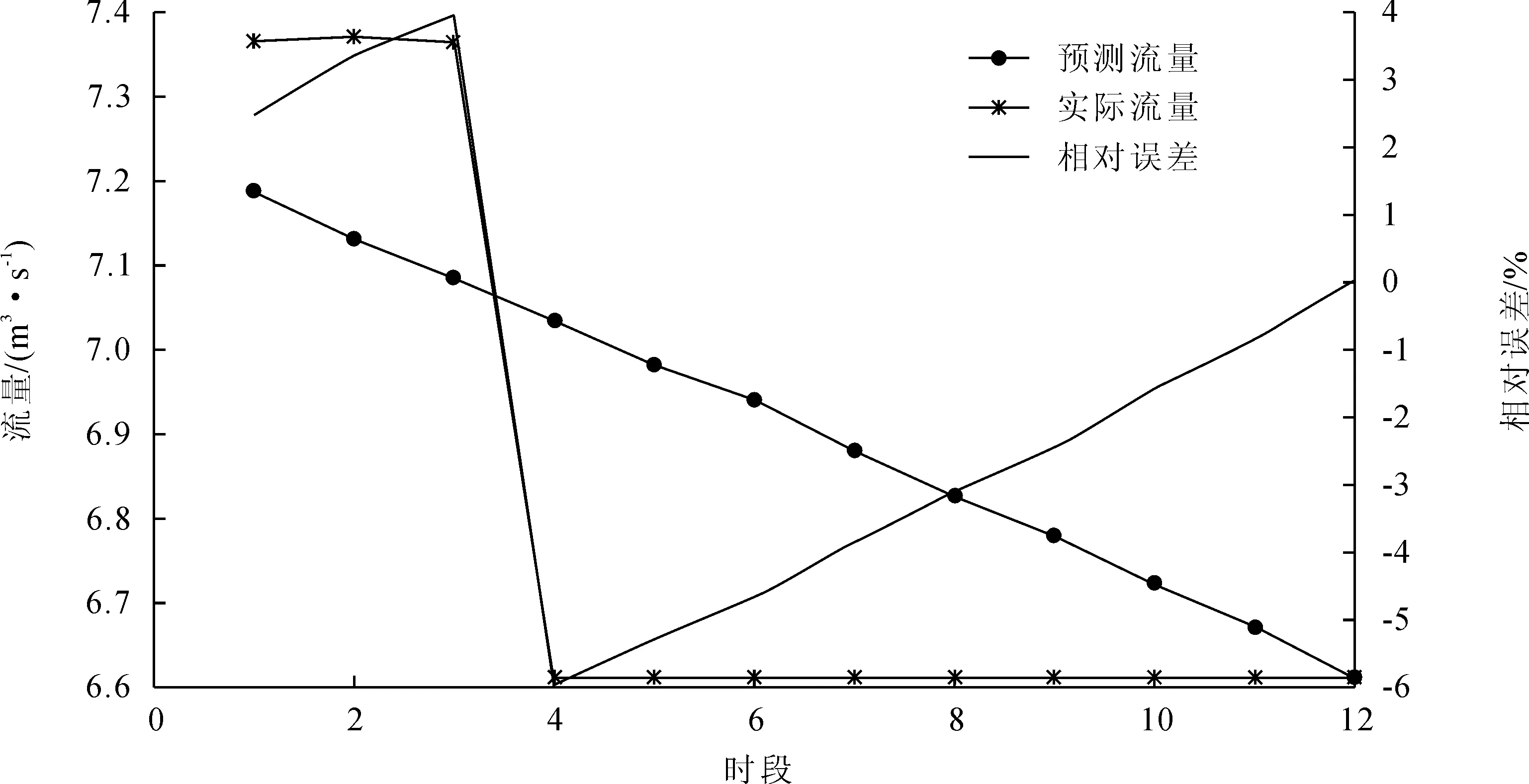
图12 资料三预测结果图(前60组训练，后12组测试)

5 结果分析

从以上结果可以看出，不论是线性神经网络还是BP神经网络，在资料一数据按照流量分组后的测试效果都比较好，相对误差均在1.5%以内，对资料二同样的训练和测试数据，两种预测方法的结果均偏小，线性神经网络比BP神经网络的相对误差都在6%以内，但线性神经网络略优；对资料三同样的训练和测试数据，测试结果BP神经网络略好，其最大相对误差为-6%，二线性神经网络的最大相对误差为7.5%。BP神经网络可以将资料一的所有数据作为训练数据，再用其中的部分时段的数据作为测试，测试数据段相对误差在±10%以内，可以作为供水期间渠首流量反演预测时参考。

6 结 语

灌区水流通常具有流量小、灌溉时间短、水位变幅小等特点，漳河总干渠又有东西库和烂泥冲两座串联水库，水位和流量变化复杂，难以准确获得。近年来漳河总干渠在信息化建设方面投入了大量的工作，使得灌区流量计量工作水平得到提高，我精准调度提供了前提。在此基础上，通过研究总干渠主要分水口的需水过程与渠首闸下泄流量的关系，科学决策渠首闸的下泄流量，对促进农业精准灌溉、节约用水、提高灌区管理水平具有重要的意义。

本文基于漳河灌区遥测系统数据库和人工补测资料数据，应用线性神经网络和BP神经网络两种方法开展了渠首闸预测下泄流量研究，研究结果表明，两种神经网络模型预测渠首闸未来下泄流量相对误差基本上均小于10%，可以在实际生产中参考应用。但在测试的过程中也发现，对测试数据与训练数据流量量级相差不大的情况下预测精度较高；另外，虽然每次的测试结果相差不大，但每次的测试结果不同，因为每次运行时都重新训练网络，重新模拟计算，具有一定的随机性，在实际应用中可取多次模拟的平均值进行预测。