海上风电抗冰锥单桩基础波浪荷载数值模拟

张 健，范荣山，金 飞

(上海勘测设计研究院有限公司，上海 200050)

中国近海风能资源的大规模开发已持续数年，而我国近海差异化的海洋环境给海上风机基础设计带来了不同的挑战。渤海和黄海北部的高纬度寒区海域风能资源丰富，在我国海上风电领域占据重要地位。寒区海上风机基础在遭受季节性海冰时，冰排作用于基础结构后破坏，产生复杂的冰荷载，对基础结构抗倾覆性能带来极大挑战。大量研究和工程实践表明，冰排在直立结构前以挤压和压屈破坏为主[1]，在倾斜锥面上以弯折破坏为主[2]，而海冰的弯曲强度小于其抗压强度，这使得作用在锥面上的水平冰荷载小于直立结构，基于此，海上风电单桩基础可采用锥体作为抗冰结构，以降低基础结构的冰荷载。

抗冰锥设置在水位变动区，由正锥体和倒锥体相扣组合而成，如图1所示。根据《中国海海冰条件及应用规定》[3]，我国渤海及黄海北部的海冰受气温、风及海流等环境因素的影响，冰期内海冰日际变化明显，基础结构在整个冰期内并非持续遭受海冰作用，无冰时环境荷载仍以波浪荷载为主，而抗冰锥的存在使基础结构阻水面积增加，增大其波浪荷载。此外，大倾角变径抗冰锥段位于水位变动区，当极端波浪作用于结构时，波浪变形严重，结构周围波浪会发生强烈的爬升、翻卷和破碎现象，导致其波浪荷载与常规单桩基础大不相同。而常规的计算圆管波浪力的Morison方程对于这样强非线性波浪荷载的系数确定则缺乏经验和实验验证。

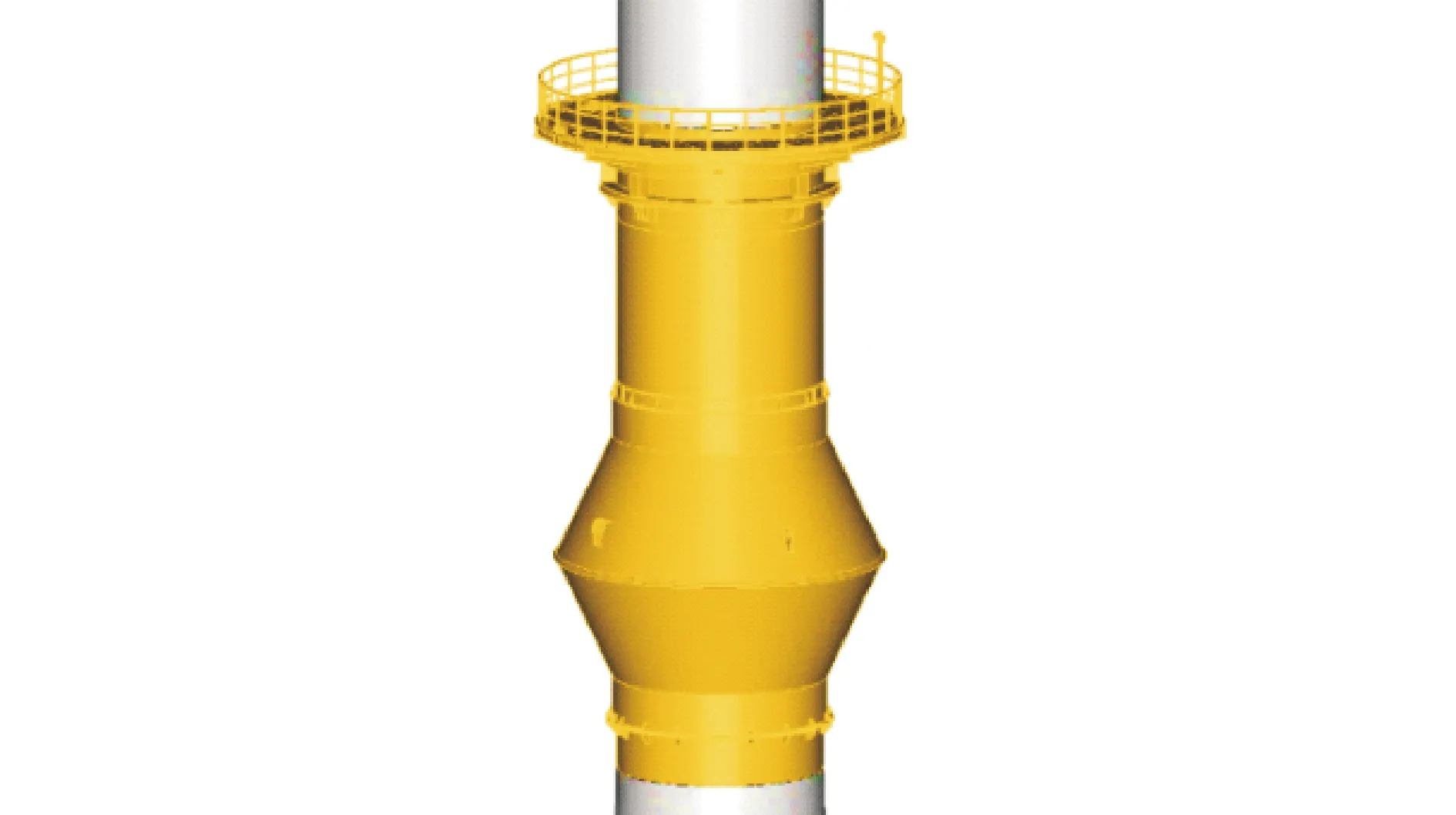
图1 抗冰锥单桩风机基础

近年来随着计算流体动力学(computational fluid dynamics，简称CFD)高精度数值计算格式的发展和计算机硬件技术的进步，使用CFD方法模拟波浪对海上结构物的作用开始大量应用于工程领域。该方法通过求解不可压缩粘性流动量守恒的运动方程，来描述复杂流场，可以模拟波浪作用于结构后的变形、破碎等现象，并计算复杂结构的波浪荷载。基于此，本文使用CFD软件Fluent建立数值波浪水槽，并在此基础上进行抗冰锥单桩基础波浪荷载的数值计算，并与无抗冰锥单桩基础的波浪荷载进行对比分析。

1 数值波浪水槽的建立与验证

类似于物理模型实验所用的波浪水槽，使用数值水槽模拟波浪对结构物的作用时，需要水槽生成稳定的目标波浪序列，同时使用适当的消波方法来消除水槽末端反射波浪对计算结果的影响。本文基于两相流模型，分别定义水相和空气相，使用流体体积函数法(volume of fluid ，简称VOF法)计算空气和水两相流体的体积分数，从而捕捉波浪的自由表面[4]。使用边界造波法在水槽入口边界上定义水质点的运动速度和波面方程实现造波。同时在水槽末端设置一定范围的消波区，在消波区动量方程中添加阻尼项[5]，使消波区波浪动能迅速衰减，水质点速度和加速度快速降低，这使得消波区内波面逐渐平静，至水槽末端几乎无波动，无法形成反射波浪，从而实现消波。

由二阶stokes波理论可知，水质点在x方向(沿波浪传播方向)和y方向(重力方向)的速度如下[6]：

(1)

(2)

波面方程为：

(3)

式中：H为波高；T为波浪周期；k=2π/L，为波数；L为波长；d为水深；ω为波浪的圆频率。

使用自定义函数功能(User defined function，简称UDF)，通过UDF的“DEFINE-PROFILE宏”将二阶stokes波的速度和波面方程赋予水槽入口的水相实现造波。通过“DEFINE-SOURCE宏”在消波区动量方程内添加阻尼项实现消波[7]。

在水槽消波区一定范围内的动量方程中添加阻尼项后，其阻尼项为：

Sx=-A1ρuf(x)f(y)

Sy=-A2ρwf(x)f(y)

式中：ρ为流体密度；x方向沿波浪传播方向；y方向沿重力方向；Sx和Sy分别为x和y方向的阻尼项；A1和A2为消波系数；xs和xe为沿波浪传播方向消波区的起点和终点坐标；yfs和yb为沿重力方向消波区的起点和终点坐标。

数值水槽各功能区布置和边界条件设置如图2所示，沿波浪入射方向将水槽划分为前端过渡区、实验区、后端过渡区和消波区。数值水槽底面和两侧面、结构表面使用壁面边界条件，满足无滑移边界条件；由于使用了边界造波法，需要在水槽入口边界处定义流体速度和波面，因此水槽入口处使用速度入口边界条件；水槽出口处在消波区内，水面几乎没有波动，满足静水压力条件，使用压力出口边界条件；水槽顶面为空气相的自由流通边界，也使用压力出口边界条件。

图2 水槽布置图

水槽内流场网格划分如图3所示，采用六面体结构化网格离散流体域，同时在自由液面附近加密网格，保证自由液面的光顺度；为了更加精确地捕捉结构附近波面的波动情况，在实验区内结构附近使用O型网格沿径向加密网格；在水槽消波区内使用沿波浪传播方向逐渐稀疏的网格，这样既能降低网格数量也能加速波浪的衰减，在一定程度上起到消波作用。

图3 流场网格

数值波浪水槽整体如图4所示，水槽长为4.5倍波长，末端消波区长为1.5倍波长，水槽宽度约为抗冰锥段最大直径的10倍，整体网格数量约133万。波浪沿X轴正方向入射，从图中可以看出：该数值波浪水槽可生成稳定的波浪序列，消波区波面平坦，几乎无波动，满足上文提到的数值水槽功能需要。可清晰模拟出波浪与抗冰锥单桩基础作用后的变形，说明当前网格划分合理。

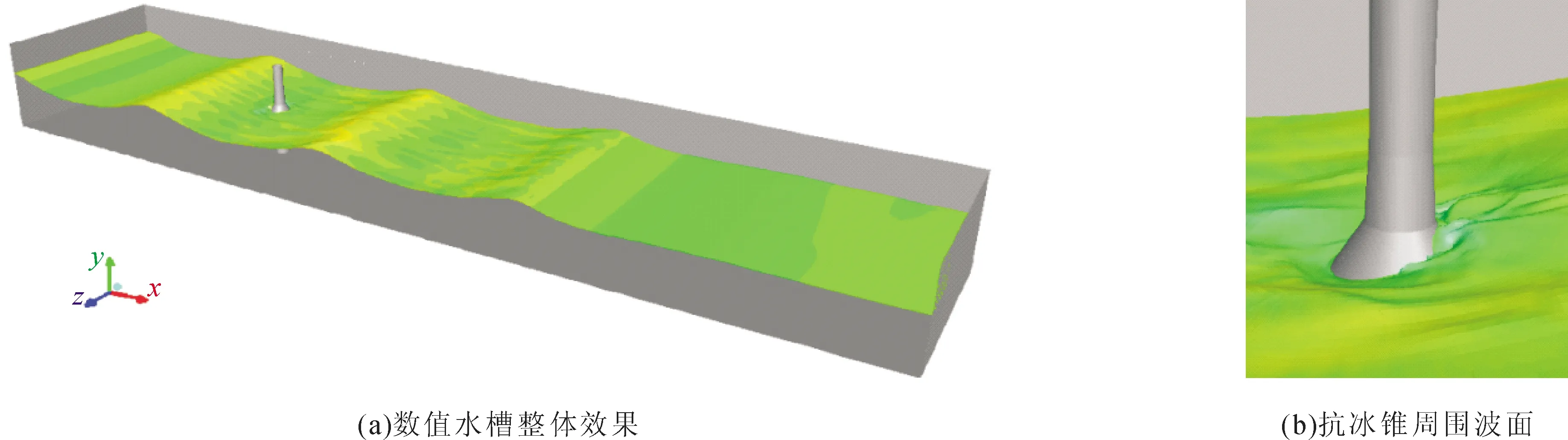
图4 数值波浪水槽速度云图

为了验证该数值水槽对抗冰锥单桩基础波浪荷载的计算精度，在数值水槽内放置与物理模型实验一致的抗冰锥段缩尺模型，计算其水平波浪力，并与实验结果进行对比。物理模型实验缩尺比为1∶20，如图5(a)所示，实验水深1.108 m，波浪周期1.75 s，波高0.365 m。数值模拟模型及波浪参数与实验保持一致，如图5(b)所示。

图5 抗冰锥段物理模型与数值模型

模型试验与数值模拟结果对比如图6所示，物理模型试验测得抗冰锥段水平波浪力极值为237.78 N，数值模拟水平波浪力极值为228.47 N，二者相对误差为3.91%，相对误差较小，表明该数值水槽可以准确计算抗冰锥单桩基础的波浪荷载。

图6 水平波浪力历时数据对比

2 某海上风电抗冰锥单桩基础波浪荷载CFD模拟

参照我国寒区海域某型风机单桩基础，分别建立包含抗冰锥单桩基础和无抗冰锥单桩基础的数值水槽，如图7所示。该单桩基础直径4.3～6 m；抗冰锥位于基础变径段，抗冰锥最大直径9.47 m，高约7.7 m，上下锥对称布置，锥角约60°。抗冰锥单桩和无冰锥单桩环境参数相同，水深22.16 m，波高7.29 m，波浪周期7.84 s。

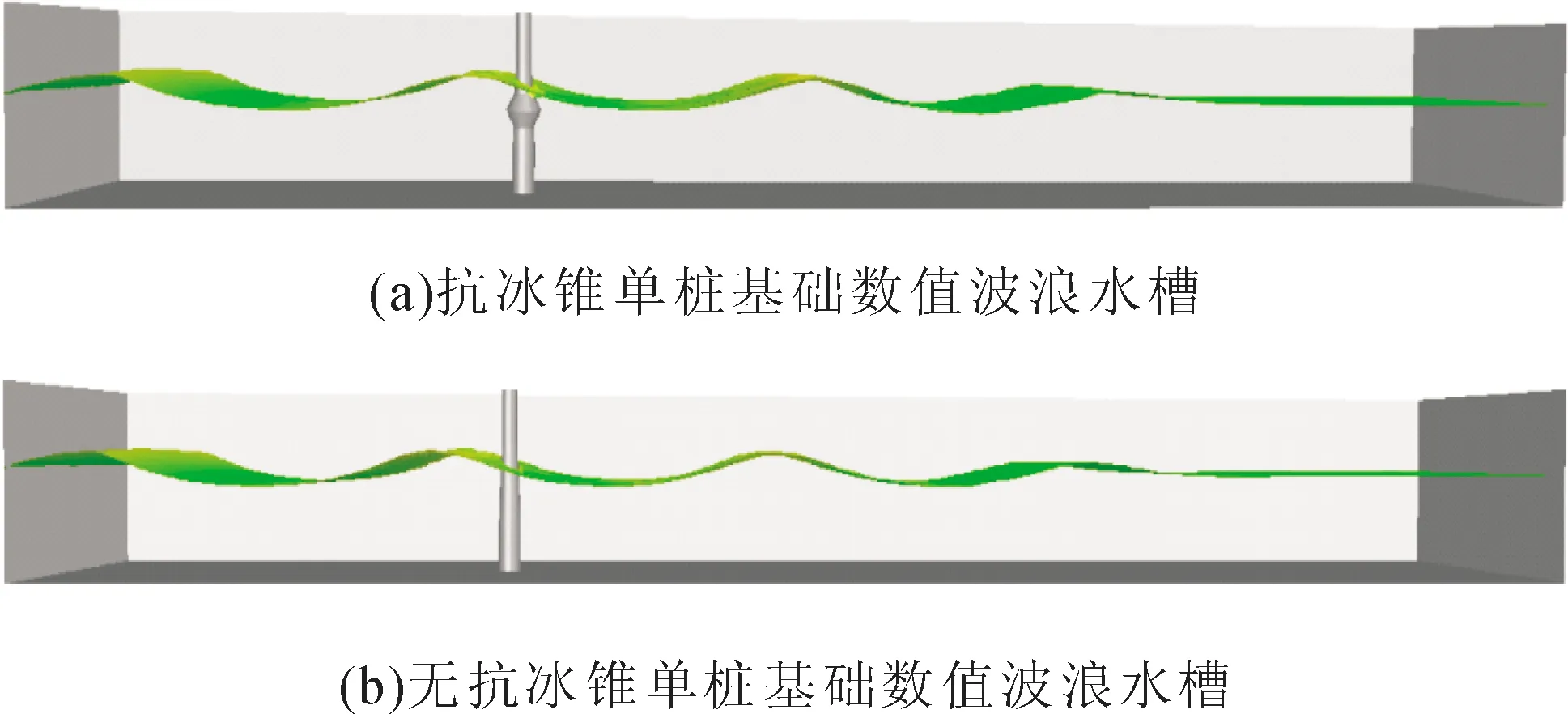
图7 数值波浪水槽

计算得到的抗冰锥单桩和无冰锥单桩基础波浪荷载如图8所示，波浪荷载的方向参照图4中坐标轴方向。

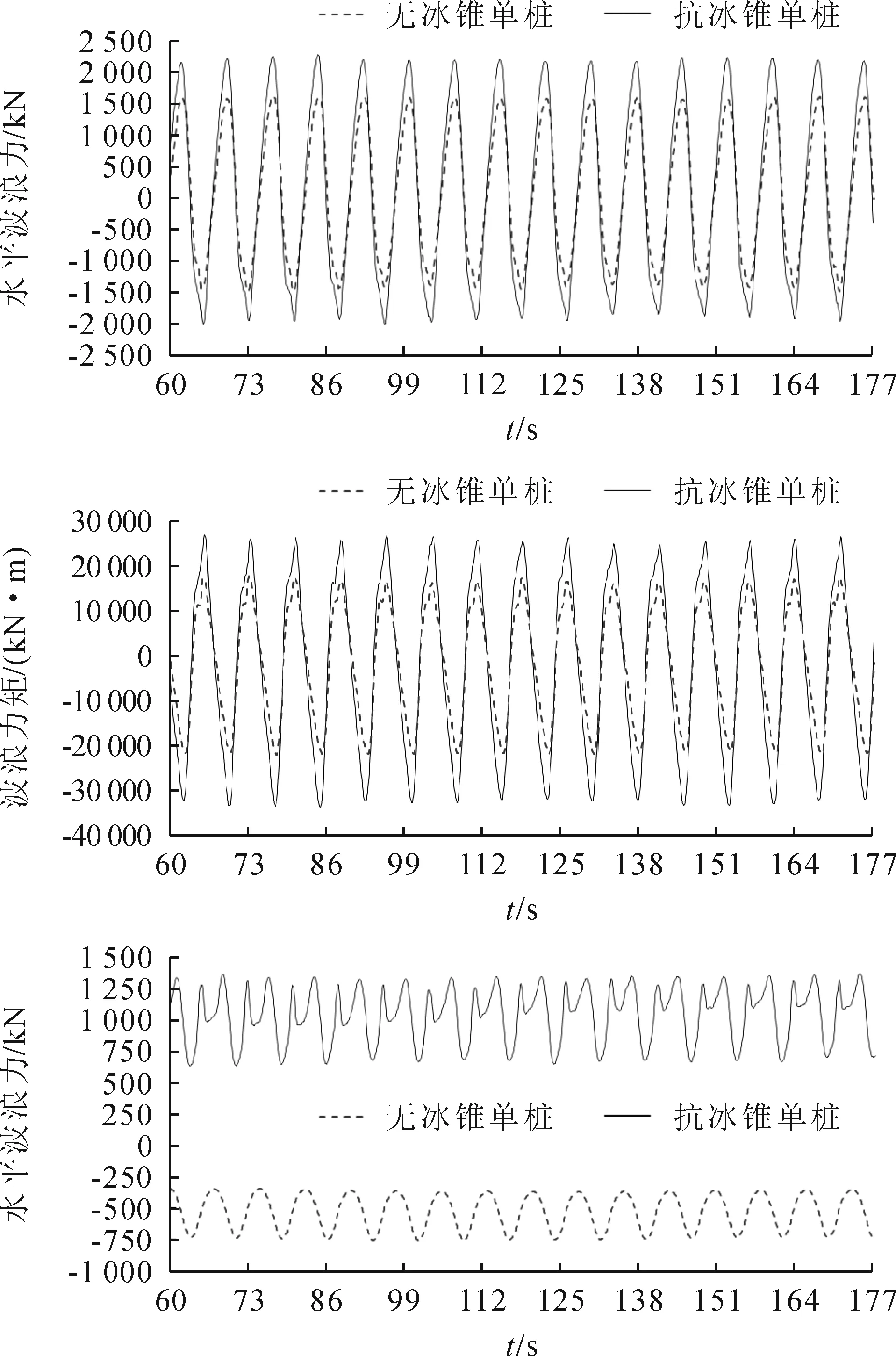
图8 波浪荷载历时数据

取15个波浪周期时段内的连续稳定波浪荷载，计算波浪荷载极值如表1所示。

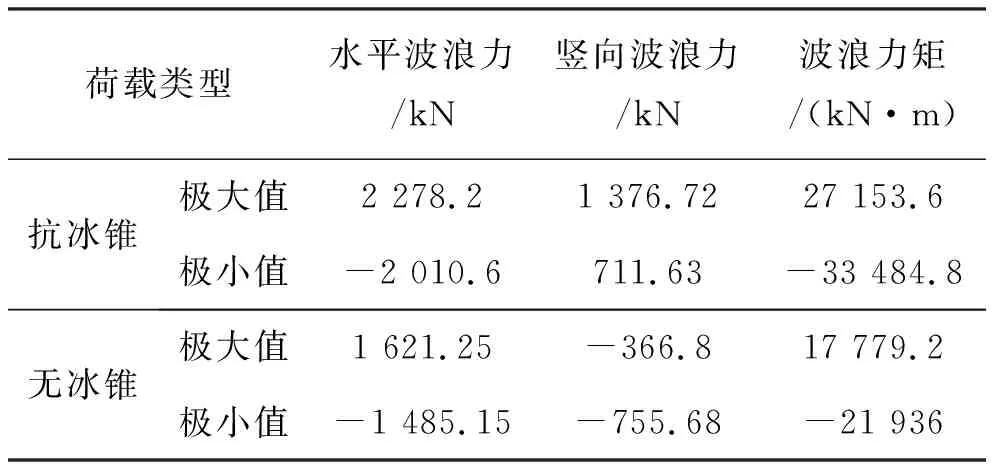
表1 波浪荷载汇总表

从波浪荷载计算结果可以看出，加装抗冰锥后，单桩基础的波浪荷载均显著增大，其中水平波浪力极值增大了40.52%，波浪力矩极值增大了52.73%，竖向波浪力极值增大了82.18%。对比正、反向水平波浪力极值发现，波浪与结构作用后，波浪的爬升、翻卷、破碎会消耗波浪能量，导致反向波浪力小于其正向值；而且由于抗冰锥段的存在导致更复杂的波浪变形，消耗更多波能，使其反向波浪荷载相对于正向波浪荷载的降低程度比无冰锥基础更大。

由于单桩基础在水中存在变径段，其竖向波浪力不可忽略，而加装大直径抗冰锥，导致基础的竖向波浪力剧烈波动，竖向波浪力历时出现了“二次波峰”现象。抗冰锥的存在还引起基础竖向波浪力的方向发生变化。这主要是因为单桩基础变径段直径随水深增大而增加(如图9(a)所示)，使变径段水压强竖直分量向下，导致无冰锥单桩基础的竖向波浪力始终向下。而加装抗冰锥后，当波峰作用于结构时，结构表面压强如图9(b)所示，抗冰锥下锥段的总压强要大于上锥段，而上下锥段的表面积相差不大，从而使上锥段竖向波浪力向下，下锥段竖向波浪力向上，下锥段竖向波浪力大于上锥段，从而导致整体结构的竖向波浪力向上；而当波谷作用于结构时，结构表面压强如图9(c)所示，上锥段大部分暴露于空气中，下锥段的水压强竖直分量向上，此时整体结构的竖向波浪力仍然向上。因此在整个波浪与抗冰锥单桩基础作用的过程中，其竖向波浪力始终向上。

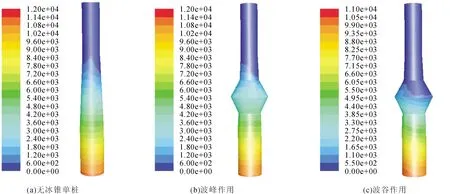
图9 单桩基础压强分布

3 结 语

本文使用CFD方法建立数值波浪水槽，该水槽能够生成目标波浪序列且消除反射波的影响。计算出抗冰锥段的水平波浪力与实验结果误差小，表明该数值水槽可用于计算抗冰锥单桩基础的波浪荷载。通过计算发现：相比较于无冰锥单桩基础，加装抗冰锥后单桩基础波浪荷载普遍增大，其中水平波浪力增大了40.52%，波浪力矩增大了52.73%，竖向波浪力增大了82.18%。抗冰锥的存在导致上下锥体出现压强差，使锥体承受两个大小不等方向相反的竖向波浪力，从而改变了原单桩基础竖向波浪力的方向。