弹丸最大射程落点诸元与弹道系数和初速关系经验公式

王 朋，王雨时，闻 泉

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

特定弹丸的阻力特性和初速确定后，最大射程落点弹道诸元包括最大射程、落速、全飞行时间和最大射程角也就可以确定了。最大射程落点弹道诸元在一定程度上代表了全弹道上各点诸元的极值，对引信和弹丸的总体论证、初步设计以及摸底试验结果分析和评估，均有一定意义。文献[1—4]给出了真空弹道条件下弹道诸元与初速的关系式。文献[5]举例定量分析了特定火炮最大射程落点诸元与初速的关系。为建立弹丸最大射程落点弹道诸元与弹丸阻力特性和初速之间的显式函数经验关系式，本文以文献[6]报道的弹丸质心外弹道计算机求解程序求解出的落点诸元数据为基础，应用SPSS软件和1stOpt软件进行数据分析和拟合。

1 拟合软件介绍及拟合原始数据

1.1 数据前处理软件

SPSS原文为“statistical package for social science”，即“社会科学统计软件包”。SPSS12.0 for Windows的运行管理方式与SPSS以前各版本基本相同。SPSS12.0 for Windows在数据整理、数据分析方面功能相比前几个版本有所增加，包括根据已知数据能够生成散点图。散点图(scatterplots)又称散布图或相关图，它是以点的分布反映变量之间相关情况的统计图形，根据图中的各点分布走向和密集程度，大致可以判断变量之间协变关系的类型[7]。

1.2 拟合软件

1stOpt(first optimization)是我国七维高科有限公司独立开发的一套数学优化分析综合工具软件包，主要用于非线性回归、曲线拟合、非线性复杂模型参数估算求解、线性/非线性规划等领域。1stOpt软件不仅操作界面简单，而且其核心计算方法——通用全局优化算法(universal global optimization,UGO)克服了当今世界上在优化设计领域使用迭代法必须给出合适初始值的难题，即不需要用户给出参数初始值，在绝大多数情况下，仅依靠自身的全局搜索能力，从任意随机值出发，就可求得最优解[8]。

1.3 拟合原始数据

按常规弹药，取弹道系数数值范围c43=0.25～4.0，取初速数值范围v0=50～1 400 m/s。以文献[6]报道的弹丸质心外弹道计算机程序为工具，求解上述弹道系数和初速数值范围内的弹丸质心空气外弹道最大射程落点诸元，结果分别如表1—表4所列。

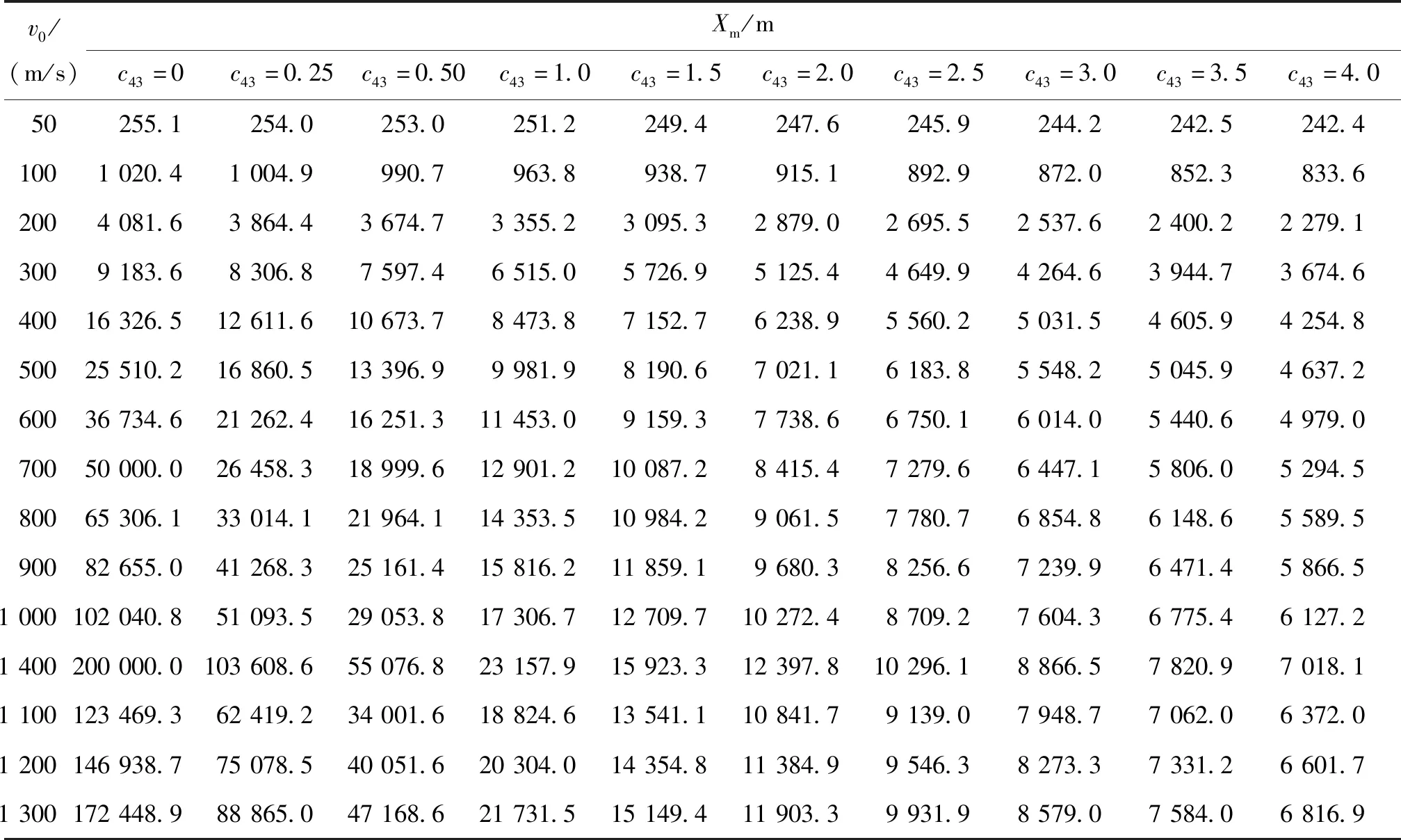
表1 弹丸最大射程Xm与弹道系数c43和初速v0之间的关系Tab.1 The relationship between the maximum range of a projectile and the ballistic coefficient and the muzzle velocity of the projectile

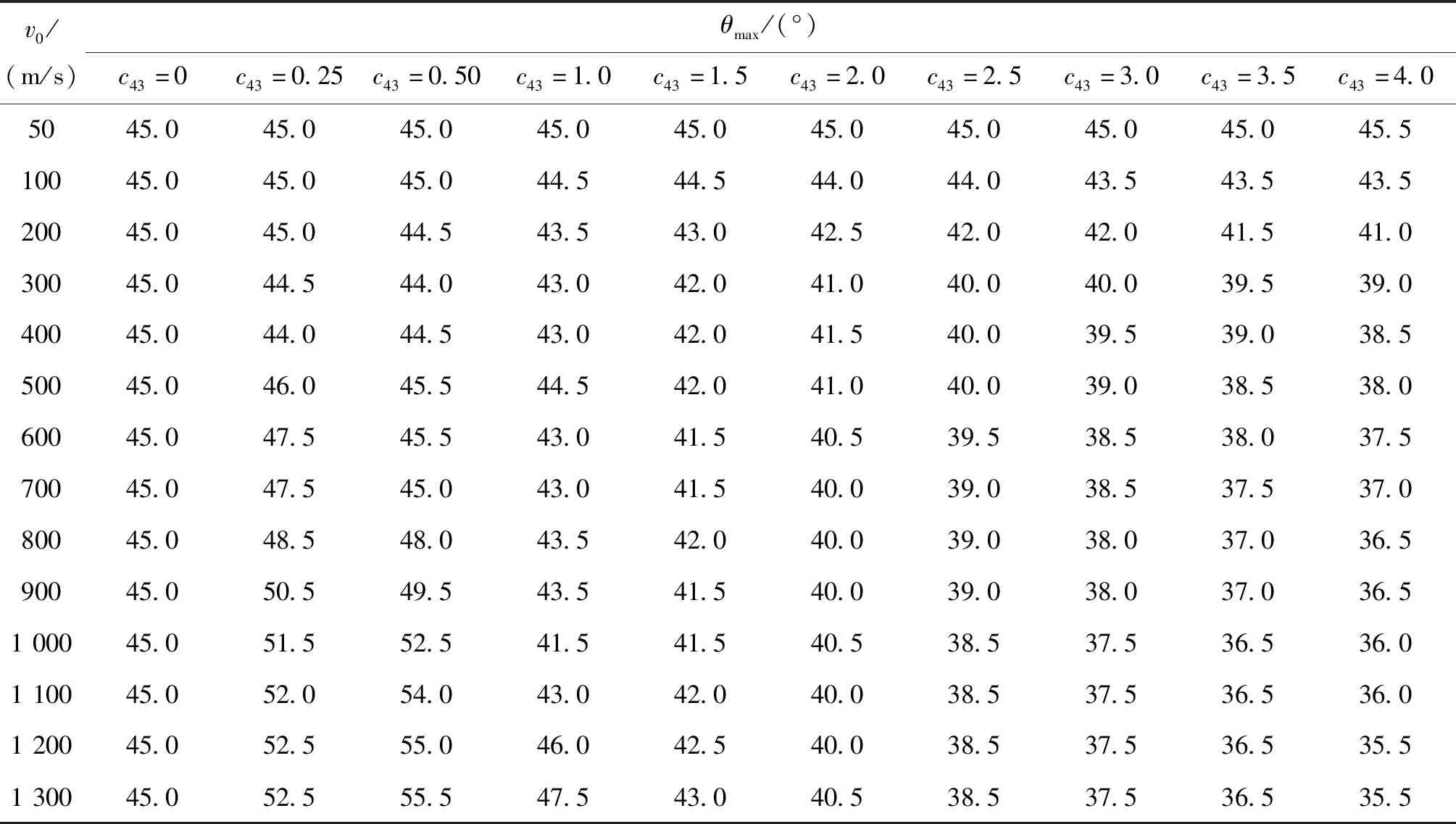
表2 弹丸最大射程角θmax与弹道系数c43和弹丸初速v0之间的关系Tab.2 The relationship between the maximum range angle of the projectile and the ballistic coefficient and the muzzle velocity of the projectile

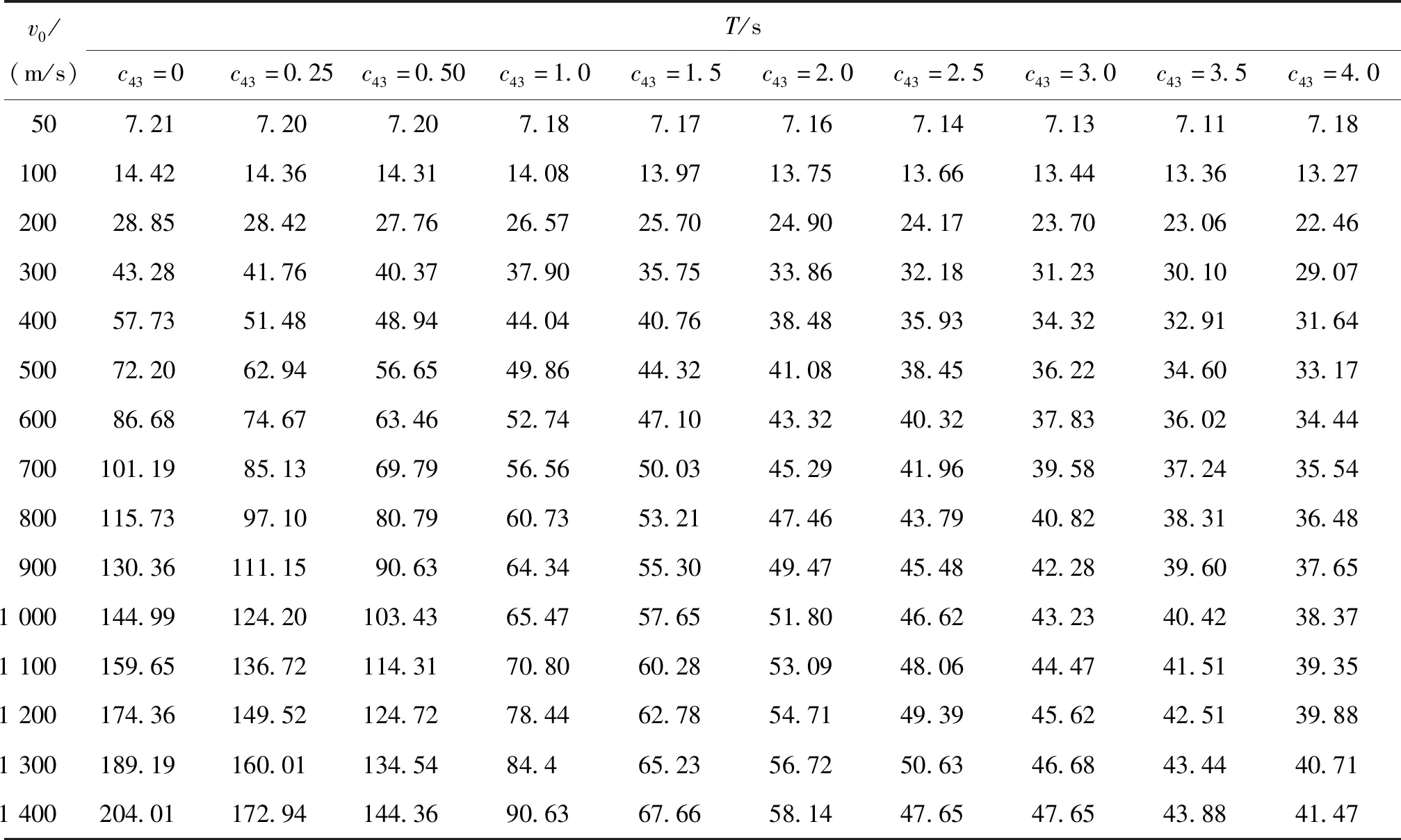
表3 弹丸全飞行时间T与弹道系数c43和弹丸初速v0之间的关系Tab.3 The relationship between the total flight time and the ballistic coefficient and the muzzle velocity of the projectile

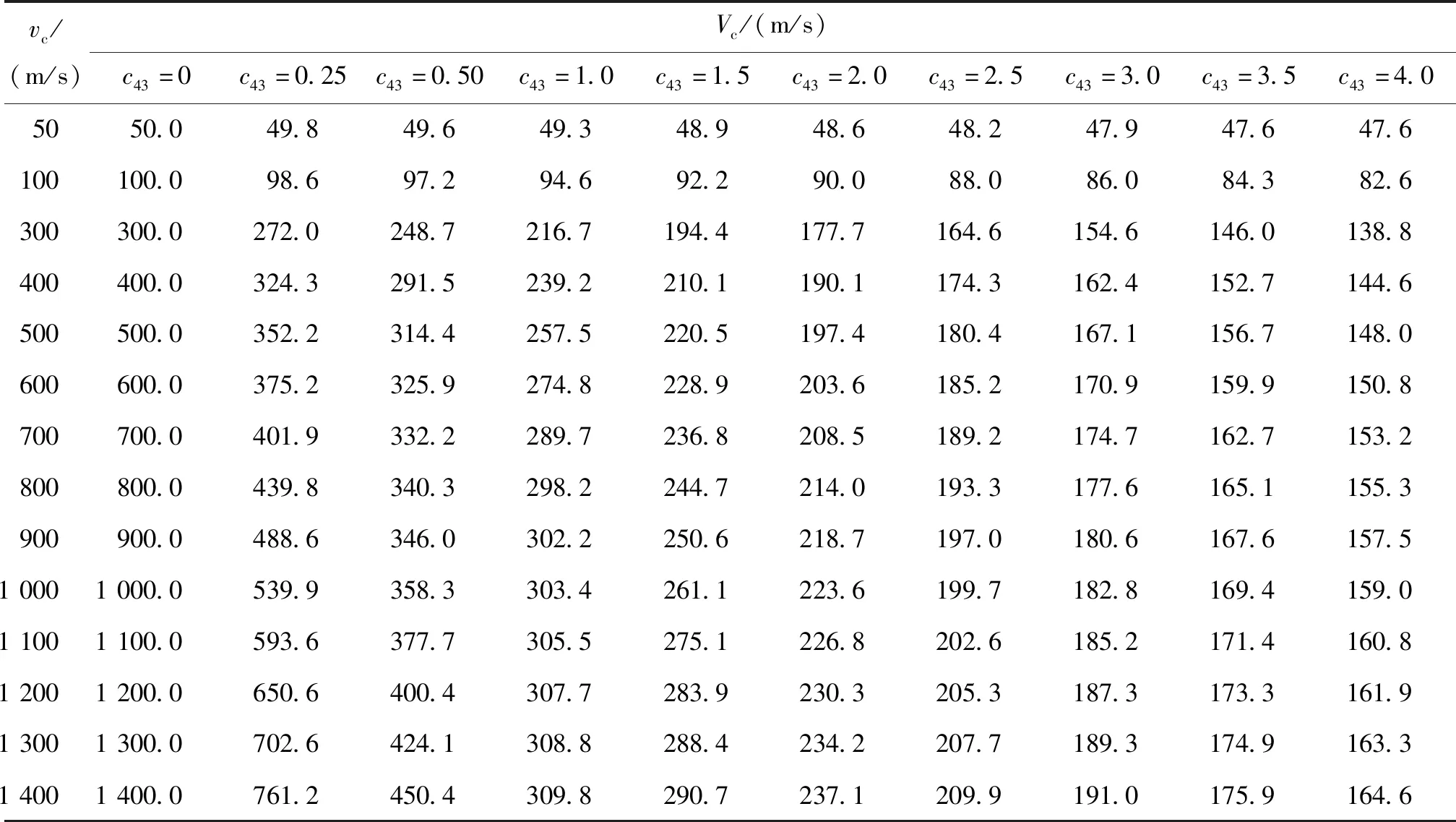
表4 弹丸最大射程落速Vc与弹道系数c43和初速v0之间的关系Tab.4 The relationship between the projectile’s maximum range falling velocity and the ballistic coefficient and the muzzle velocity

应用该程序的计算结果是可信的[6]。表中弹道系数c43的计量单位是m2/kg，初速和落速v0的计量单位是m/s，射程的计量单位是m，时间的计量单位是s。

2 弹丸全飞行时间、落速、最大射程角和最大射程与弹道系数和初速关系式的经验拟合

2.1 最大射程与弹道系数和初速关系拟合

通过表1给出的数据，由SPSS12.0 for Windows验证弹道系数和初速与最大射程之间的相关性，得出弹道系数和初速的显著性小于0.001，其中弹道系数与最大射程是负相关，初速与最大射程是正相关。文献[5]通过试验数据拟合得出火炮最大射程和弹丸初速近似呈线性关系的结论。弹道系数和弹丸初速这两个影响因子共同对火炮最大射程的影响就变得极为复杂。

由于此模型未知，应用1stOpt软件进行自动拟合即在函数库中自主选择拟合公式，算法选择通用全局优化算法和麦夸特法，得到最佳的拟合公式的形式为：

Xm=

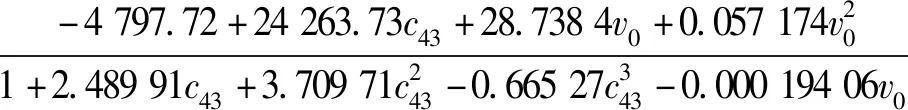
(1)

拟合后的曲线如图1所示。

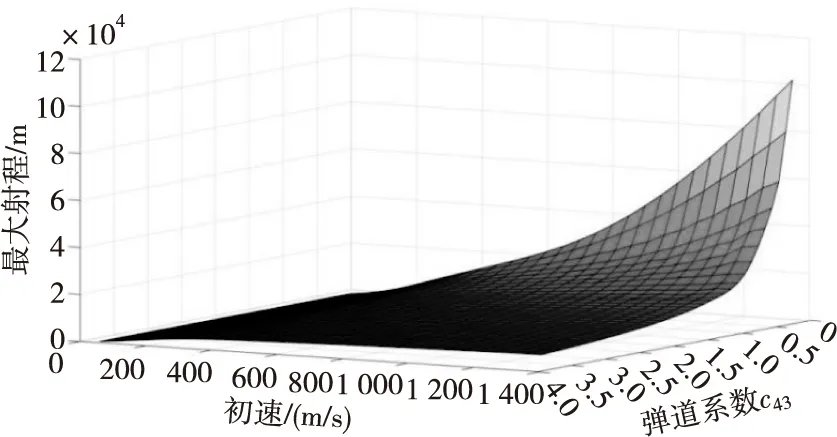
图1 弹道系数和初速与最大射程的拟合曲线Fig.1 The fitted curve for ballistic coefficient and muzzle velocity with maximum range of artillery

当c43=0时，拟合公式为：

Xm=

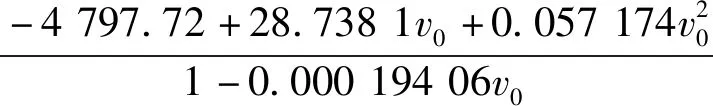
(2)

取c43=0,同时取v0分别为50、700、1 400 m/s，得到真空弹道条件下的最大射程值和原有数据对比误差如表5所列。

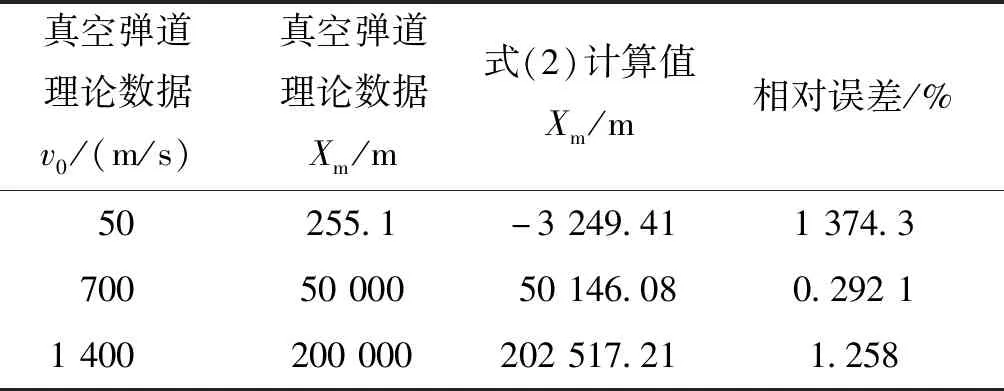
表5 最大射程拟合后的公式与原数据的相对误差Tab.5 The relative error between the maximum range fitting formula and the original data

2.2 最大射程角与弹道系数和初速关系拟合

在空气弹道中，由于受到外弹道阻力的影响，落角的绝对值肯定会比射角大。文献[5]中得到了在误差允许的范围内，拟合后弹丸落角与弹丸初速近似呈线性关系，初速越大，落角绝对值也越大。

目前未见到有弹道系数和初速与最大射程角之间的关系，因而使用1stOpt软件自带的自动搜索匹配公式的功能进行拟合，经过分析对比选用的拟合公式为：

(3)

拟合后的关系式为：

θmax=

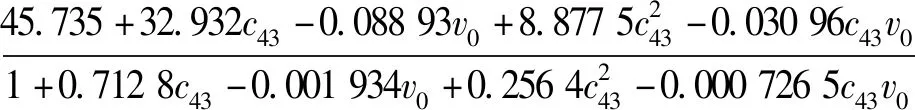
(4)

拟合后的曲线如图2所示。

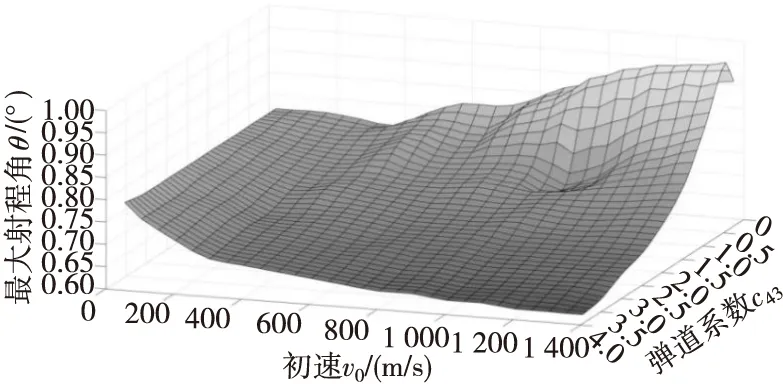
图2 弹道系数和初速与最大射程角的拟合曲线Fig.2 The fitted curve for ballistic coefficient and muzzle velocity with the falling angle of maximum range of artillery

当c43=0时，拟合公式为：

(5)

取c43=0,同时取v0分别为50、700、1 400 m/s，得到真空弹道条件下的最大射程角和原有数据对比误差如表6所列。

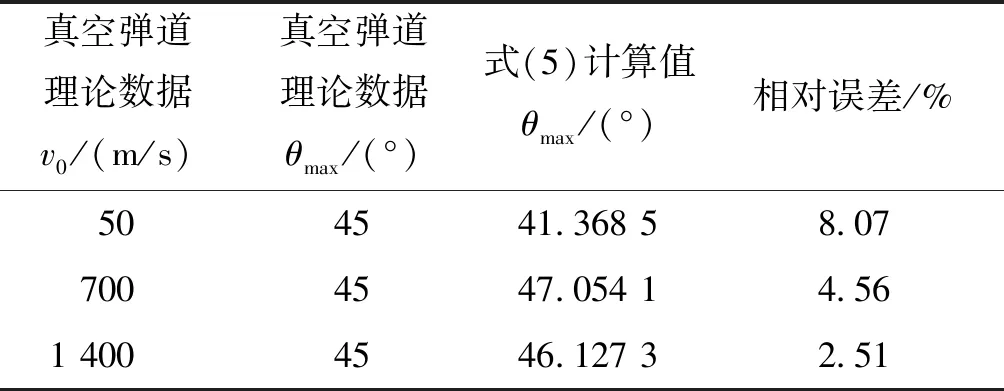
表6 最大射程角拟合后的公式与原数据的相对误差Tab.6 The relative error between the maximum range angle fitting formula and the original data

2.3 弹丸全飞行时间与弹道系数和初速关系拟合

根据表3给出的数据，由SPSS12.0 for Windows验证弹道系数和初速与全飞行时间的相关性，得出弹道系数和初速的显著性系数小于0.001，弹道系数与全飞行时间呈负相关，初速与全飞行时间呈正相关。由文献[5]可知，弹丸全飞行时间与弹丸初速近似呈线性关系,从图3可以清楚地看出弹道系数和初速与全飞行时间是多元非线性的关系。

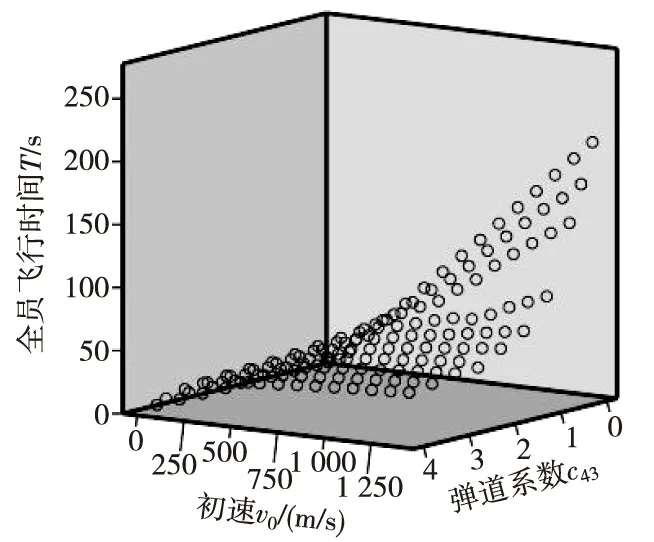
图3 弹道系数和初速与全飞行时间的散点图Fig.3 The scatter diagram of ballistic coefficient and muzzle velocity with full flight time

由于此模型未知，应用1stOpt软件进行自动拟合即在函数库中自主选择拟合公式，算法选择通用全局优化算法和麦夸特法，得到最佳的拟合公式的形式为：

T=

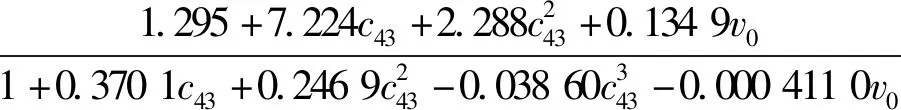
(6)

拟合后的曲线如图4所示。

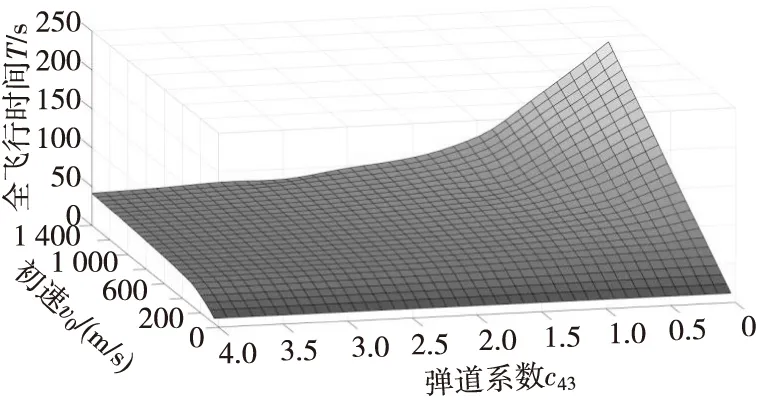
图4 弹道系数和初速与全飞行时间的拟合曲线Fig.4 The fitted curve for ballistic coefficient and muzzle velocity with full flight time

当c43=0时，拟合公式为：

(7)

取c43=0,同时取v0分别为50、700、1 400 m/s，得到真空弹道条件下的全飞行时间和原有数据对比误差如表7所列。

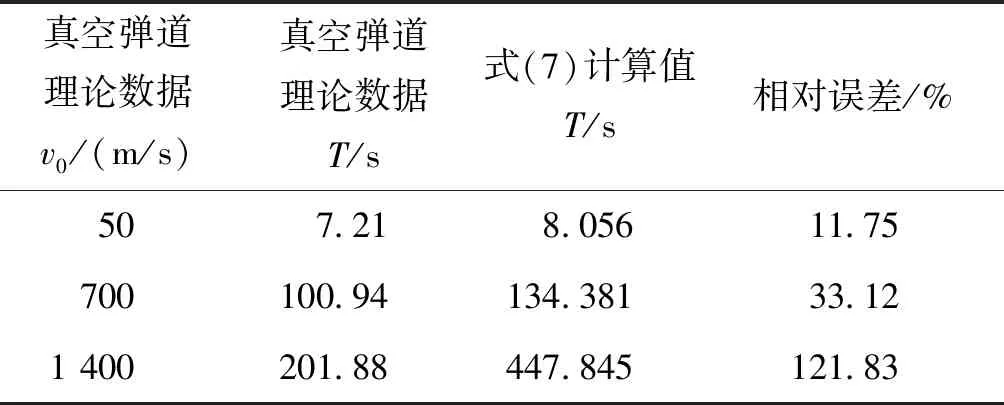
表7 全飞行时间拟合后的公式与原数据的相对误差Tab.7 The relative error between full flight time fitting formula and the original data

2.4 落地速度与弹道系数和初速关系拟合

根据表4给出的数据，由SPSS12.0 for Windows验证弹道系数和初速与落地速度的相关性，得出弹道系数和初速的显著性系数小于0.001，弹道系数与落地速度呈负相关，初速与落地速度呈正相关。从图5可以清楚地看出弹道系数和初速与落地速度是多元非线性的关系。

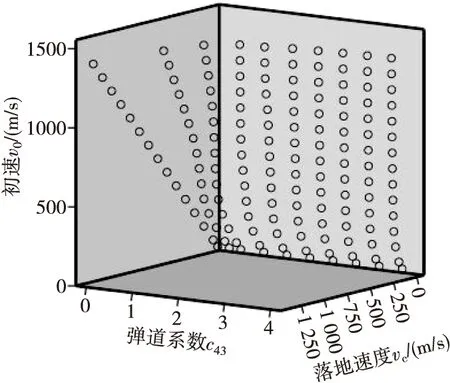
图5 弹道系数和初速与落地速度的散点图Fig.5 The scatter diagram of ballistic coefficient and muzzle velocity with landing speed

由于此模型未知，应用1stOpt软件进行自动拟合即在函数库中自主选择拟合公式，算法选择通用全局优化算法和麦夸特法，得到最佳的拟合公式的形式为：

vc=

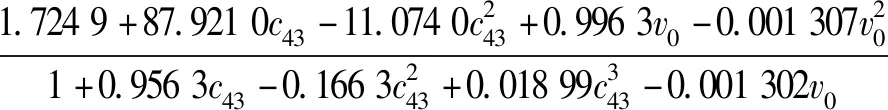
(8)

拟合后的曲线如图6所示。

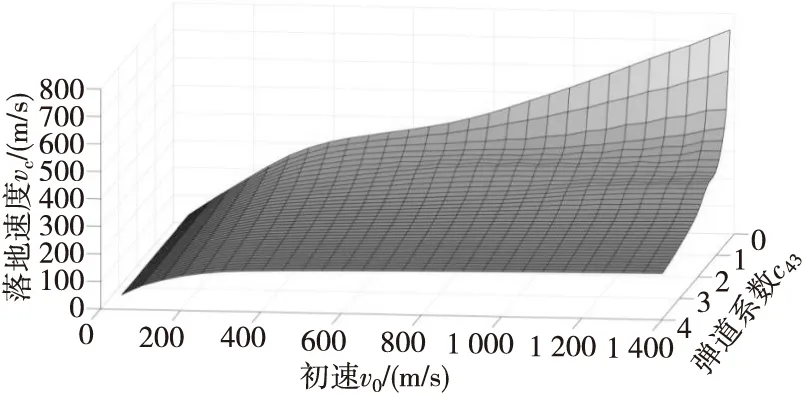
图6 弹道系数和初速与落地速度的拟合曲线Fig.6 The fitted curve for ballistic coefficient and muzzle velocity with landing speed

当c43=0时，拟合公式为：

(9)

取c43=0,同时取v0分别为50、700、1 400 m/s，得到真空弹道条件下的落地速度和原有数据对比误差如表8所列。

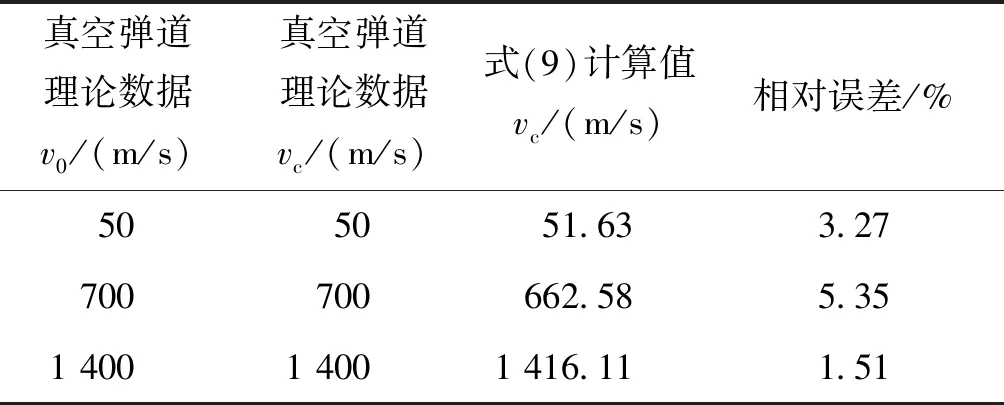
表8 落地速度拟合后的公式与原数据的相对误差Tab.8 The relative error between landing speed fitting formula and the original data

3 分析与讨论

在拟合弹道系数和初速与落地速度、全飞行时间、最大射程和最大射角关系经验拟合公式时，R方拟合优度接近于1。由弹道系数和初速拟合出来的公式来验证其可信度，拟合数据结果如表9所列。

表9 拟合后弹道诸元的数据结果Fig.9 The data result of fitted post-ballistic element

由于要求拟合关系式的R方拟合度尽量接近于1，所以选取拟合公式较为复杂。利用SPSS12.0 for Windows和1stOpt来验证弹道系数和初速与全飞行时间、落地速度、最大射程角和最大射程关系经验拟合的相关性。由于各种火炮的空气弹道规律大体上是相同的，所得基本规律对于其他火炮同样适用，应该具有普适性，有助于弹药和引信总体论证、初步设计、性能分析和试验评估的外弹道特性估算参考。

在处理多元非线性拟合分析时，需要先判断自变量之间是否相关；若相关，再分析出相关自变量的函数关系来降低维数。由于自变量与因变量之间的函数关系未知，本文又是两个不相关自变量与单个因变量的非线性拟合，采用1stOpt软件进行三维非线性拟合，迭代过程中以R方拟合优度为标准，越接近1，拟合程度越好，设置迭代的次数，拟合算法选择通用全局优化算法和麦夸特法(非线性最小二乘法)。拟合算法的选取标准是使迭代过程中迭代次数越少且拟合的程度越好。

4 应用举例

为验算由弹道系数和初速拟合出的经验公式的适用范围和准确度，用以下三个算例来检验得出的公式。

已知某122 mm榴弹炮普通榴弹初速v0=402 m/s,弹道系数c43=0.689,最大射程落点诸元的值分别为全飞行时间T=47.05 s、落地速度vc=269.16 m/s、最大射程角θmax=44°和最大射程Xm=9 720 m/s。将122 mm榴弹炮普通榴弹炮的初速和弹道系数代入由弹道系数和初速拟合出的经验公式，得出的计算值与原有值的相对误差如表10所列。

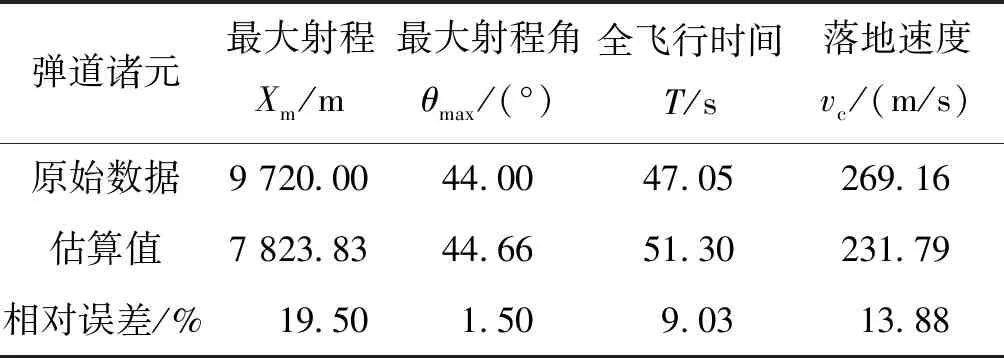
表10 122 mm榴弹炮普通榴弹外弹道诸元经验公式估算结果Tab.10 The empirical formula estimation results of the 122 mm howitzer projectile exterior ballistics firing data

已知某120 mm迫击炮普通榴弹初速v0=272 m/s,弹道系数c43=0.788 5,最大射程落点诸元的值分别为全飞行时间T=35.34 s、落地速度vc=214.10 m/s、最大射程角θmax=43°和最大射程Xm=5 889.26 m/s。将120 mm迫击炮普通榴弹炮的初速和弹道系数代入由弹道系数和初速拟合出的经验公式，得出的计算值与原有值的相对误差如表11所列。

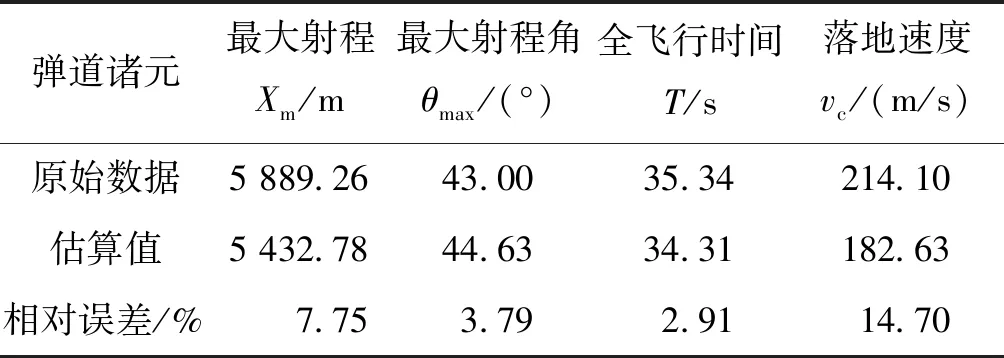
表11 120 mm迫击炮普通榴弹外弹道诸元经验公式估算结果Tab.11 The empirical formula estimation results of the 120 mm mortar ordinary grenade exterior ballistics firing data

已知某155 mm加榴炮普通榴弹初速v0=325 m/s,弹道系数c43=0.6,最大射程落点诸元的值分别为全飞行时间T=41.68 s，落地速度vc=251.95 m/s，最大射程角θmax=43°和最大射程Xm=8 200 m/s。将155 mm加榴炮普通榴弹炮的初速和弹道系数代入由弹道系数和初速拟合出的经验公式，得出的计算值与原有值的相对误差如表12所列。

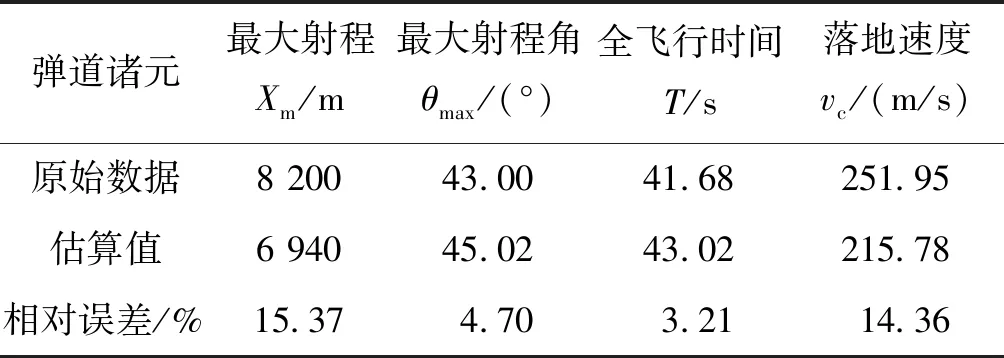
表12 155 mm加榴弹炮普通榴弹外弹道诸元经验公式估算结果Tab.12 The empirical formula estimation results of the 155 mm gun-howitzer projectile exterior ballistics firing data

5 结论

本文提出了利用SPSS12.0 for Windows和1stOpt分别对炮弹的弹道系数，包括初速与全飞行时间、落地速度、最大射程角和最大射程等进行了相关性分析和经验公式拟合，提出了利用拟合函数关系得到具有较高精度的快速弹道诸元近似预估值的方法。拟合结果表明：全飞行时间、落地速度和最大射程角的均方根误差比较小，预测值跟真实值接近，得出的函数关系式可信；最大射程的均方根误差较大，预测模型描述实验数据的精确度不高，但是R方拟合优度最接近于1，拟合趋势最接近于真实的情况；弹道系数越小，初速越大，弹丸的全飞行时间就越长，落地速度、最大射程角和最大射程越大。可在信息量偏少时，用于引信和弹药初步设计、性能和质量分析、试验数据评估与鉴别等。