非标准气象条件对计转数定距引信炸点精度的影响

刘艳欣，王雨时，闻 泉，王光宇

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

弹丸外弹道转速衰减规律直接影响着计转数定距引信的定距精度，乃至弹丸的外弹道设计。如果要得到较为精确的弹丸质心外弹道转速衰减规律，就必须建立更加符合实际的数学模型。文献[1]介绍了第二次世界大战以来关于弹丸转速衰减规律的经验公式，如范特柴里公式、柔格里公式、板口楯雄推荐式等。文献[2]根据现代弹丸飞行稳定性与工程实际对修正过的柔格里公式等作了进一步推导，得到了幂函数公式和指数函数公式。这些经验公式反映了弹丸转速衰减的基本规律。文献[3—4]针对由圆台、拱形与圆柱组成的弹丸外形，建立了质心外弹道运动方程组和转速衰减规律数学模型。文献[5]针对由半球形、圆柱形组成的弹丸外形，建立了旋转弹丸外弹道转速衰减模型。文献[6]针对准抛物线形头部轮廓母线旋转弹丸外形，建立了弹丸外弹道转速衰减模型。这些数学模型从本质上揭示了这类特定外形弹丸转速衰减规律的基本特性，具有一定的指导意义，但都是在标准气象条件下建立的。文献[7]以斜切尾翼弹为算例，通过推导导转力矩与极阻尼力矩计算公式，建立了弹丸转速衰减规律数学模型，但并未分析气温、气压、风速与海拔高度对定距精度的影响。文献[8—9]通过风洞试验得到了极阻尼力矩系数，建立了弹丸转速衰减规律数学模型，但风洞试验成本较高。

针对上述问题，本文将应用外弹道学理论和空气动力学知识，建立非标准气象条件下(包括气温、气压、风速、海拔高度)弹丸质心外弹道数学模型和转速衰减规律数学模型，并应用Matlab软件以小口径弹丸为例进行数值计算，研究气温、气压、风速、海拔高度对弹丸外弹道转速衰减规律的影响。

1 非标准气象条件下的旋转弹丸外弹道转速衰减规律数值仿真模型

1.1 非标准气象条件分析

标准气象条件是指气象诸元的地面值为标准值(即气温15 ℃，气压100 kPa，风速0 m/s，海拔高度0 m，空气密度1.206 kg/m3)且这些气象条件随高度变化符合标准定律[10]。非标准气象条件是指气象条件不仅随地点变化，而且在同一地点还随高度变化[10]。本文中的非标准气象条件是指气温的地面值在范围-40～+50 ℃内变化，气压的地面值在范围88～100 kPa内变化，风速的地面值在范围0～25 m/s内变化，海拔高度的地面值在范围0～1 000 m内变化，且空中分布也会随这些气象条件的地面值不同而改变。这些非标准气象条件的分布将在下面进行介绍。气温、气压包含于密度函数H(y)，气压函数π(y)与声速cs中，风速包含于弹丸相对速度中。此外，气温亦包含于气体密度ρ与空气黏度系数μ中。针对常规弹丸外弹道涉及的对流层，下面介绍密度函数H(y)、气压函数π(y)、弹丸相对速度vr(vwx，vwy，vwz)以及气体密度ρ与空气黏度系数μ的表达式。

1.1.1密度函数、气压函数与声速函数表达式

在对流层内，非标准气象条件下的气温随高度变化的表达式为[11]：

(1)

式(1)中：Tv1为非标准气象条件下的气温；Tv0为地面气温；G1为与气温有关常数，取6.328×10-3[10]；y为弹丸飞行高度；Tv0n为标准气象条件下的地面气温，取288.9 K[4]；ΔTv为弹道温差，即地面实际气温与标准气象条件下的气温之差。

由文献[11]可知，在对流层内，非标准气象条件下的气压函数表达式为：

(2)

式(2)中：P0为非标准气象条件下的地面气压值；P0n为标准条件下的气压值，取为100 kPa；g为重力加速度，取为9.806 65 m/s2；R为气体常数，取为287.05 J/(kg·K)。

由式(2)可知，在对流层内，非标准气象条件下的气体密度函数表达式为[11]：

(3)

式(3)中：ρ0n为标准气象条件下的空气密度，取为1.206 3 kg/m3。

在对流层内，非标准气象条件下的声速函数表达式为[11]：

(4)

式(4)中：k为绝热指数，取1.404。

1.1.2弹丸相对速度vr

如图1所示，以炮口为原点O、以海平面为基准面建立Oxyz坐标系。平面Oxy为弹丸射击平面，弹丸速度v与y轴的正向呈θ夹角，vwx、vwz分别为纵风与横风。

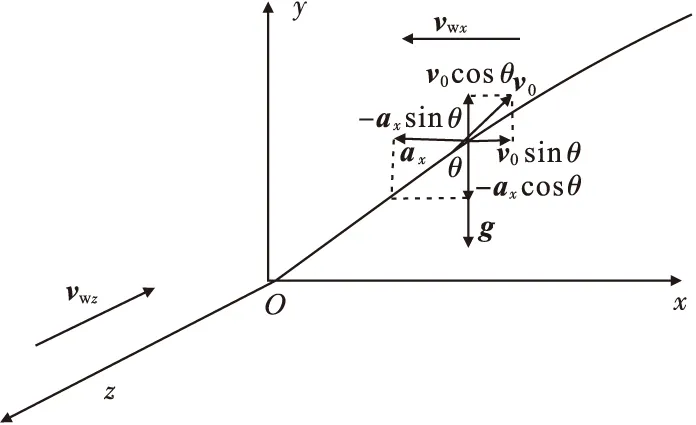
图1 弹丸质心外弹道运动坐标系Fig.1 The movement coordinate system of the centroid external ballistics of the projectile

由外弹道学理论可知，纵风和横风的大小分别为[10]：

(5)

式(5)中：vw为风速，αN为射击方向与正北方向的夹角，αw为风向与正北方向的夹角，负号“-”表示风速与弹丸飞行速度相反。

弹丸相对速度vr为：

(6)

1.1.3气体密度与空气黏度系数表达式

由式(3)可知，气体密度表达式为：

ρ=H(y)ρ0n

(7)

由文献[5]可知，标准气象条件下的空气黏度系数μ的表达式为：

(8)

式(8)中：βa为常数，取1.458×10-6kg/(s·m·K0.5)；Ts为常数，取110.4 K；τ为标准条件下的气温函数。

将式(1)代入式(8)可得非标准气象条件下的空气黏度系数μv1的表达式为：

(9)

1.2 非标准气象条件下的旋转弹丸外弹道转速衰减规律数学模型

1.2.1弹丸表面产生的摩擦力矩

将式(6)代入弹丸极阻尼力矩表达式[10]得：

(10)

式(10)中：ω为弹丸自转角速度，rad/s；d为弹丸直径，m；S为弹丸横截面积，m2，其表达式为：S=πd2/4。

弹丸摩阻cxf的表达式为[10]：

(11)

式(11)中：Ss为弹丸侧面积，m2。

形状修正系数ηλ的表达式为[10]：

(12)

式(12)中：l为弹丸长度，m。

考虑空气可压缩性的修正系数ηm的表达式为[10]：

(13)

式(13)中：a为常数，其表达式为[10]：

雷诺系数Re的表达式[10]为：

马赫数Ma表达式为：

1.2.2弹带产生的摩擦力矩

由文献[6]可知，弹带的计算公式为：

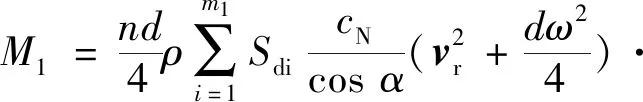
(sinα1sinα2+cosα1cosα2)

(14)

式(14)即为非标准气象条件下的旋转弹丸外弹道转速衰减规律数学模型。该模型为一阶非线性微分方程，无解析解，须联立非标准气象条件下的弹丸质心外弹道数学模型求解。

1.3 数值仿真模型

文献[11]给出了非标准气象条件下的弹丸质心外弹道方程组，联立式(10)和式(14)可得：

(15)

式(15)中：t为弹丸飞行时间，s；x为弹丸水平飞行距离，m；y为弹丸飞行高度，m；z为弹丸偏离弹道平面侧向位移，m；vx为弹丸速度在x轴方向的分量，m/s；vy为弹丸速度在y轴方向的分量，m/s；vz为弹丸速度在z轴方向的分量，m/s；θ为弹道倾角，(°)；m为弹丸质量，kg；cx0为零升阻力系数，由仿真求得。

式(15)即为非标准气象条件下的旋转弹丸外弹道转速衰减规律数值仿真模型。该模型求解的初始条件为：当t=0时，vx=v0cosθ0，vy=v0sinθ0，vz=0，θ=θ0，x=z=0，y=y0，ω=ωg，P=P0。

2 模型可信性验证

下面以105 mm坦克炮实弹射击试验结果来验证非标准气象条件下旋转弹丸外弹道转速衰减规律数值仿真模型的可信性。试验用弹为杀爆弹，弹长485.46 mm，直径105 mm，平均弹重16.136 kg。试验5发，射角0.7 °，装定炸点转数534。应用多普勒脉冲式雷达测得膛口速度，通过设立靶杆的方法测得炸点距离。表1给出了105 mm口径弹丸数值仿真用参数。表2给出了105 mm口径弹丸数值仿真结果与靶试结果。

表1 105 mm口径杀爆弹弹丸外弹道数值仿真用参数Tab.1 External ballistic numerical simulation related parameters of the 105-caliber projectile

由表2可知，仿真所得弹丸炸点距离相对于实测值的误差较小。因此，本文建立的非标准气象条件下旋转弹丸外弹道转速衰减规律数值仿真模型具有可信性。

表2 在非标准气象条件下105 mm口径杀爆弹弹丸装定转数534时的炸点距离数值仿真结果和靶试结果Tab.2 Numerical simulation results and target test results of projectile burst distance under non-standard meteorological conditions

3 小口径旋转弹丸非标准气象条件下外弹道转速衰减规律计算

基于非标准气象条件下的旋转弹丸外弹道转速衰减规律数值仿真模型，以30 mm口径旋转弹丸为算例，研究气温、气压、风速(顺风和逆风)以及海拔高度对计转数引信定距精度的影响。

3.1 物理模型

根据30 mm口径旋转弹丸的外形，可将其划分为四个基本单元，分别为圆台形、拱形、圆柱形和弹带部，如图2所示。

图2 30 mm口径榴弹弹丸外形Fig.2 A 30-caliber grenade projectile shape

3.2 弹丸数值仿真参数

表3列出了30 mm口径榴弹弹丸数值仿真的相关参数。

表3 30 mm口径弹丸外弹道数值仿真相关参数Tab.3 External ballistic numerical simulation related parameters of the 30-caliber projectile

式(12)中的弹丸阻力系数cx0是影响外弹道的重要参数之一，与弹丸外形密切相关。由外弹道学知识可知，cx0是关于弹丸马赫数的函数。为了得到更为准确的弹丸阻力系数，采用了Fluent软件对该30 mm口径弹丸的外形空气动力学特性进行了仿真，并采用OriginLab软件对所得阻力系数进行了曲线拟合，所得结果见式(16)。

(16)

3.3 非标准气象条件下弹丸转速衰减规律数值仿真

为了得到弹丸的外弹道诸元，将式(16)代入式(15)，采用Matlab软件编写程序，并通过龙格-库塔算法进行数值仿真[12]。

3.3.1气温对计转数引信定距精度影响分析

假设气温的变化范围为-40～+50 ℃，以-40、-25、-10、+5、+20、+35、+50 ℃为例对弹丸外弹道转速衰减规律数学模型进行数值仿真并对引信定距精度进行分析。假设弹丸的初速为960 m/s、射角为20°、弹重为0.346 kg、气压为100 kPa、风速为0 m/s、海拔高度为0 m，以地面气温15 ℃时引信装定炸点距离500、1 000、1 500、2 000、2 500 m为标准条件，可仿真得到不同气温时的弹丸炸点距离，如表4所列。图3给出了以地面气温15 ℃时引信装定炸点距离500、1 000、1 500、2 000、2 500 m为基准，气温对定距精度的影响。图中横坐标T为地面气温值，纵坐标Δx为炸点距离变化量。

表4 不同气温时的炸点距离仿真结果Tab.4 The simulation results of burst distance at different temperatures m

由图3可知：弹丸炸点距离的变化与地面气温的变化方向相同，即地面气温越高，弹丸炸点距离变化就越大；在地面气温小于15 ℃时，引信装定炸点距离越大，弹丸炸点距离变化越小；当地面气温大于15 ℃时，引信装定炸点距离越大，弹丸炸点距离变化越大。因此，引信定距精度随气温的增大，先升高后降低，随装定距离的增大而降低，当引信装定距离小于1 000 m时，可认为气温对引信定距精度的影响较小。

图3 气温对定距精度的影响Fig.3 The influence of the temperature on the precision of fixed distance

3.3.2气压对计转数引信定距精度影响分析

假设气压的变化范围为88～100 kPa，以88、90、92、94、96、98 kPa为例对弹丸外弹道转速衰减规律数学模型进行数值仿真并对引信定距精度进行分析。假设弹丸的初速为960 m/s，射角为20°，弹重为0.346 kg，气温为15 ℃，风速为0 m/s，海拔高度为0 m，以气压值100 kPa时引信装定炸点距离500、1 000、1 500、2 000、2 500 m为标准条件，可仿真得到不同气压时的弹丸炸点距离，如表5所列。图4给出了以气压值100 kPa时引信装定炸点距离500、1 000、1 500、2 000、2 500 m为基准，气压对定距精度的影响。图中横坐标P0为地面气压值，纵坐标Δx为炸点距离变化量。

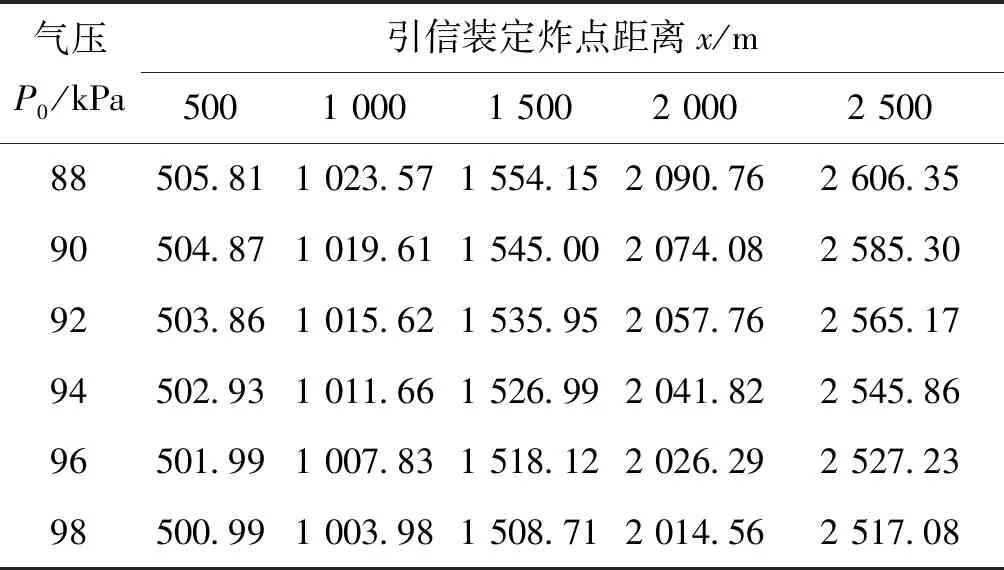
表5 不同气压时的炸点距离仿真结果Tab.5 The simulation results of burst distance at different atmospheric pressures m

由图4可知：弹丸炸点距离的变化与地面气压值的变化方向相反，即地面气压值越大，弹丸炸点距离变化就越小；弹丸炸点距离的变化与引信装定距离的变化方向相同，即引信装定炸点距离越大，弹丸炸点距离变化越大。因此，引信定距精度随气压值的增大而升高，随装定距离的增大而降低，当引信装定距离小于1 000 m时，可认为气压对引信定距精度的影响较小。

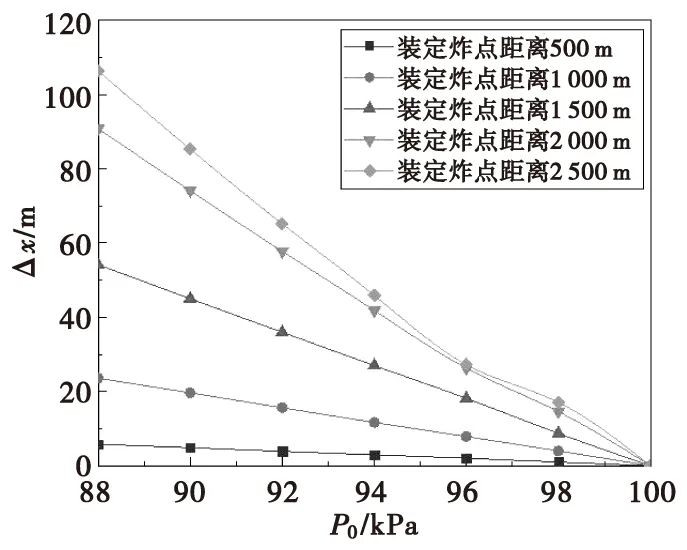
图4 气压对定距精度的影响Fig.4 The influence of the atmospheric pressure on the precision of fixed distance

3.3.3风速对计转数引信定距精度影响分析

假设风速的变化范围为0～25 m/s，以5、10、15、20、25 m/s为例对弹丸外弹道转速衰减规律数学模型进行数值仿真并对引信定距精度进行分析。假设弹丸初速为960 m/s、射角为20°，弹重为0.346 kg，气温为30 ℃，气压100 kPa，海拔高度为0 m，以无风时引信装定的炸点距离500、1 000、1 500、2 000、2 500 m为标准条件，可仿真得到不同风速时的弹丸炸点距离，如表6所列。图5、图6分别给出了以无风时引信装定炸点距离500、1 000、1 500、2 000、2 500 m为基准，顺风和逆风对定距精度的影响。图5中横坐标vw+为顺风，纵坐标Δx为炸点距离变化量；图6中横坐标vw-为逆风，纵坐标Δx为炸点距离变化量。

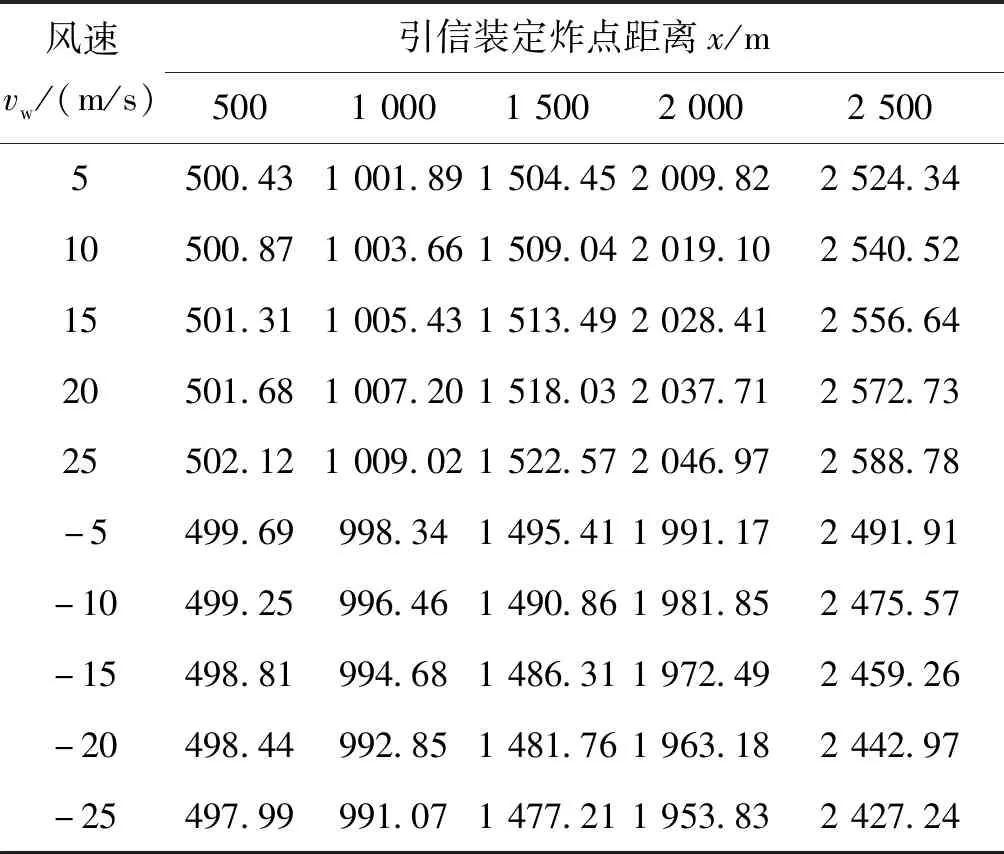
表6 不同风速时的炸点距离仿真结果Tab.6 The simulation results of burst distance at different wind m

图5 顺风对定距精度的影响Fig.5 The influence of along the wind on the precision of fixed distance

由图5可知：弹丸炸点距离的变化与vw+大小的变化方向相同，即vw+越大，弹丸炸点距离变化就越大；弹丸炸点距离变化与引信装定距离的变化方向相同，即引信装定炸点距离越大，弹丸炸点距离变化越大。因此，引信定距精度随顺风速与装定距离的增大而降低，当引信装定距离小于1 500 m时，可认为顺风速对引信定距精度的影响较小。

由图6可知：弹丸炸点距离的变化与vw-大小的变化方向相同，即vw-越大，弹丸炸点距离变化就越大；弹丸炸点距离的变化与引信装定距离的变化方向相反，即引信装定炸点距离越大，弹丸炸点距离变化越小。因此，引信定距精度随逆风速与装定距离的增大而降低，当引信装定距离小于1 500 m时，可认为逆风速对引信定距精度的影响较小。

图6 逆风对定距精度的影响Fig.6 The influence of the inversus wind on the precision of fixed distance

综上所述，弹丸炸点距离变化与风速的变化方向相同，与逆风速时引信装定距离的变化方向相反，与顺风速时引信装定距离的变化方向相同。因此，引信定距精度随风速与装定距离的增大而降低，当引信装定距离小于1 500 m时，可认为风速对引信定距精度的影响较小。

3.3.4海拔高度对计转数引信定距精度影响分析

假设海拔高度的变化范围为0～1 000 m，以200、400、600、800、1 000 m为例对弹丸外弹道转速衰减规律数学模型进行数值仿真并对引信定距精度进行分析。假设弹丸的初速为960 m/s，射角为20°，弹重为0.346 kg，气温为15 ℃，气压100 kPa，风速为0 m/s，以海拔高度0 mm时引信装定的炸点距离500、1 000、1 500、2 000、2 500 m为标准条件，可仿真得到不同海拔高度时的弹丸炸点距离，如表7所列。图7给出了以海拔高度0 mm时引信装定炸点距离500、1 000、1 500、2 000、2 500 m为基准，海拔高度对定距精度的影响。图中横坐标y0为海拔高度，纵坐标Δx为炸点距离变化量。

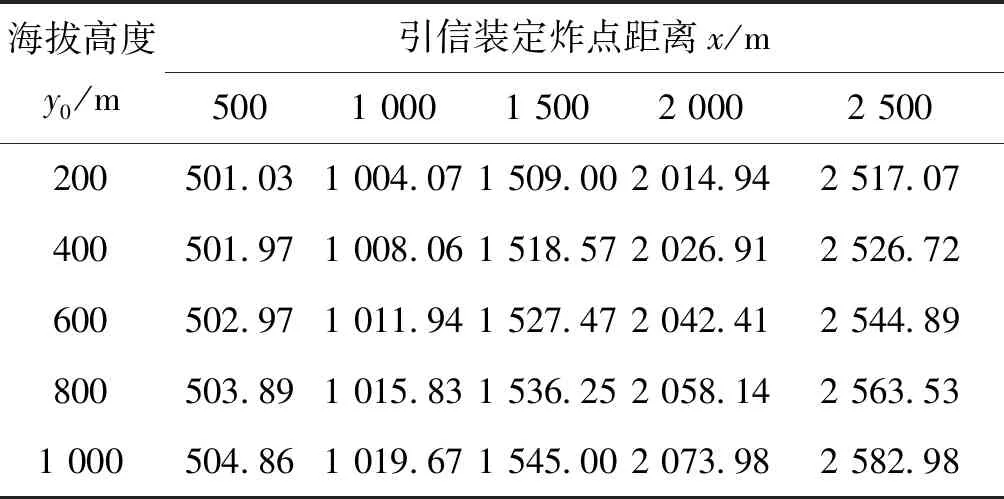
表7 不同海拔高度时的炸点距离仿真结果Tab.7 The simulation results of burst distance at different altitudes m

由图7可知：弹丸炸点距离的变化与海拔高度的变化方向相同，即海拔高度越大，弹丸炸点距离变化就越大；弹丸炸点距离变化与引信装定距离的变化方向相同，即引信装定炸点距离越大，弹丸炸点距离变化越大。因此，引信定距精度随海拔高度与装定炸点距离的增大而降低，当引信装定距离小于1 000 m时，可认为海拔高度对引信定距精度的影响较小。

图7 海拔高度对定距精度的影响Fig.7 The influence of the altitude on the precision of fixed distance

4 结论

本文在考虑气温、气压、风速(顺风、逆风)以及海拔高度的条件下建立了非标准气象条件下(包括气温、气压、风速以及海拔高度)弹丸质心外弹道数学模型和转速衰减规律数学模型，并应用Matlab软件针对30 mm口径弹丸进行数值计算，研究了气温、气压、风速以及海拔高度对弹丸外弹道转速衰减规律的影响。结果表明：引信外弹道计转数定距精度随气温的增大，先升高后降低，随气压的增大而升高，随风速的增大而降低，随海拔高度的增大而降低。这些气象条件对引信外弹道计转数定距精度的影响随装定炸点距离的增大而降低。当引信装定距离小于1 000 m时，气温、气压、风速与海拔高度对引信外弹道计转数定距精度影响较小。