联合卫星重力、卫星测高及陆地重力异常构建高分辨率地球重力场模型SGG-UGM-2

梁伟，李建成,b，徐新禹,b,*，张胜军，赵永奇

a School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China

b Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China

c School of Resources and Civil Engineering, Northeastern University, Shenyang 110004, China

1. 引言

高分辨率地球重力场模型可用于高精度大地水准面确定、全球高程基准统一、动态海面地形确定和地球内部结构探测等科学和工程应用研究[1-5]。随着新一代卫星重力计划（Challenging Minisatellite Payload,CHAMP）的出现[6]以及重力场与气候实验卫星（Gravity Recovery and Climate Experiment, GRACE）[7]和重力场与海洋环流探测卫星（Gravity field and Steady-State Ocean Circulation Explorer, GOCE）[8]的成功发射，地球重力场模型的中长波精度得到了显著提高[9-16]；同时，地面重力数据、卫星测高数据、航空重力数据和地形数据包含了高精度的短波信号[17]，因此可以联合卫星、测高和地面等多源重力数据解算高精度、高分辨率的地球重力场模型。

国际地球重力场模型中心（International Center for Global Earth Models, ICGEM; http://icgem.gfz-potsdam.de/tom_longtime）发布的高分辨率地球重力场模型有：Earth Gravitational Model (EGM) 2008 [18]、European improved gravity model of the earth by new techniques (EIGEN)-6C4 [19]、GOCE and EGM2008 Combined model（GECO） [20]、gravity observation combination (GOCO)模型GOCO05c [21]、Experimental Gravity Field Model(XGM) 2016 [22]和SGG-UGM-1 [23]，表1给出了这些模型的属性。由于这些模型使用了新一代重力卫星的数据，模型的中长波精度得到了显著提高。EGM2008是当前使用最多的重力场模型，它的计算中使用了几乎精度最高的5′×5′分辨率全球重力异常和ITG-GRACE03S模型的法方程，但是并没有用到GOCE卫星的数据；其中全球重力异常数据融合了地面重力数据、卫星测高数据和地形数据。EIGEN-6C4是EIGEN系列模型的代表，相较于EGM2008，它使用了GOCE卫星数据和Laser Geodynamics Satellite (LAGEOS)卫星数据，不过地面重力异常数据由EGM2008模型计算。EGM2008和EIGEN-6C4的高阶次系数都是采用块对角最小二乘法解算得到，而720阶次GOCO05c和719阶次的XGM2016是联合卫星和重力异常法方程，采用严格最小二乘方法估计的。GECO和SGG-UGM-1都是通过使用GOCE数据精化EGM2008模型得到[22-24]。文献[23]的检核结果表明EGM2008、EIGEN-6C4和SGG-UGM-1在美国的精度接近，而包含GOCE数据的EIGEN-6C4和SGG-UGM-1在中国的精度优于EGM2008。

本文将介绍的SGG-UGM-2模型与SGG-UGM-1同属一个系列的高分辨率重力场模型，它是SGG-UGM-1模型的进一步发展，采用椭球谐分析方法计算，并使用新的海域重力异常数据，以及融入GRACE卫星观测法方程，以此提升模型的精度。

由于地球更接近于椭球，球近似的误差要大于椭球近似，所以在全球重力场模型计算中往往将地面重力数据延拓到参考椭球面上，如Ohio States University (OSU)91 [25]、EGM96 [26]和EGM2008 [18]，因此椭球谐分析比球谐分析更适合于椭球面数据的处理[27]。Hotine[28]和Jekeli [29,30]对第二类勒让德函数进行了规格化，并推导了球谐系数与椭球谐系数之间的转换公式（下文称为“Jekeli转换”或“Jekeli系数转换”）。Gleason [31]通过数值试验验证了Jekeli转换的精度。Sebera等[32]将勒让德函数的计算扩展至二阶导数，并减少了计算超几何变换需要的迭代次数。

在基于椭球面重力异常构建全球重力场模型时，一般首先对椭球面的重力异常数据进行椭球谐分析得到椭球谐系数，然后将椭球谐系数转换为扰动位的球谐系数（Csnm），本文将这种计算重力场模型的方法简称为EHACT (Ellipsoidal Harmonic Analysis and Coefficients Transformation) 方法。EHA-CT方法可能有不同具体实现策略，例如，可以通过最小二乘方法进行椭球谐分析，也可以使用数值积分方法实现椭球谐分析。Rapp和Pavlis[33]推导了使用椭球面平均重力异常数据计算系数Csnm的计算公式，该公式用在了OSU89 [33]、OSU91 [25]、EGM96 [26]、IGG97LB [34]和MOD99 [35]等模型的计算中。前述ICGEM发布的高分辨率重力场模型中，只有EGM2008是使用椭球谐分析计算的，在EGM2008的求解中，首先使用了最小二乘方法进行椭球谐分析得到椭球谐系数（），然后使用Jekeli转换将转换为。本文将首先介绍EHA-CT方法，并推导相关的严密公式，及引入Driscoll和Healy [36]的采样理论，得到适用于离散点值的严密积分公式。需要指出的是，本文推导的适用于格网均值的积分公式和文献[33]推导的公式略有不同。此外，需要说明的是：由椭球面重力异常数据计算重力场模型属于椭球边界面大地测量边值问题的范畴，除EHA-CT方法之外，文献[36-43]也给出了其他解算方法。

海域面积占地球表面的71%，高精度的海域重力异常是构建高分辨率重力场模型的关键，越来越多的卫星测高数据可以用于海域重力异常的确定，如Geosat GM /ERM (17 d), ERS-1/GM (168 d), ERS/ERM (35 d), T/P/T/P Tandem (10 d), Jason-1/ERM (10 d), Envisat (35d/30 d),Jason-2/ERM (10 d), Jason-1/GM (406 d), CryoSat-2 (369 d),SARAL/AltiKa ERM(35 d), HY-2A (14 d), Jason-2/GM 和SARAL/AltiKa GM。由这些多星测高数据可以使用数值分析方法[44,45]或者最小二乘配置方法[46,47]计算得到纬度-80.738°～80.738°范围内1′×1′空间分辨率的重力异常数据，用于高分辨率地球重力场模型的解算。本文使用卫星测高数据计算了海洋区域1′×1′的重力异常数据，并与EGM2008计算的陆地重力异常数据融合，组成了全球重力异常格网数据集。除此之外，GRACE卫星提供了长达15年的卫星重力观测数据，使用这些数据可以计算高精度的重力场长波信号。ITSG-Grace2018 [48]是ITSG(Institute of Theoretical Geodesy and Satellite Geodesy)系列GRACE重力场模型的最新模型，模型的作者将模型的法方程与模型同时发布，本文将利用该法方程与其他类型的重力数据一起用于高分辨率重力场模型的解算。SGGUGM-1中使用的海域重力异常来自EGM2008，且没有用到GRACE数据，SGG-UGM-2的解算中将使用新的海域重力异常数据和ITSG-Grace2018模型法方程。

表1 ICGEM发布的高分辨率重力场模型的主要属性

本文分为6个部分，首先在第2部分介绍EHA-CT方法的基本原理，并推导相应的计算公式；在第3部分使用数值试验对本文推导的公式进行验证；第4部分介绍SGG-UGM-2模型的具体计算过程；第5部分给出模型的检核结果；最后在第6部分进行总结。

2. 基本原理与方法

2.1. 由椭球面重力异常数据求解重力场模型系数的EHA-CT方法

任意满足拉普拉斯方程的调和函数f在其调和区域内可用椭球谐函数级数表示为[30,32]：

式中，(u, δ, λ)为椭球坐标[1]；E为参考椭球的线性偏心率；b为参考椭球的短半轴；Ynm(δ, λ)为完全正规化的面球谐函数：

调和函数rΔg的椭球谐展开式为[31,33]：

式中，rΔg为r和Δg的积，r为地心向径，Δg为重力异常；为rΔg的椭球谐展开系数；a为参考椭球的长半径。

当重力异常数据位于参考椭球面上时，式（2）可简化为：

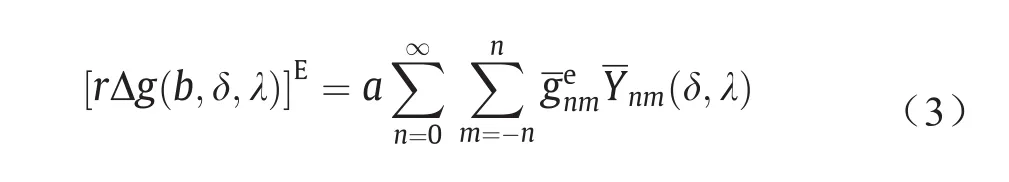
式中，[]E表示数据位于参考椭球表面。

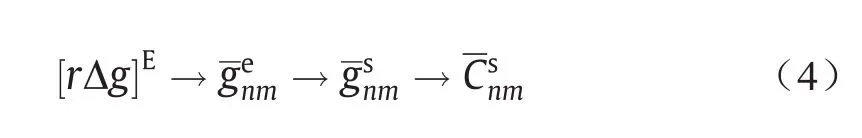
式（4）所示的系数转换方法为，首先使用Jekeli系数转换将系数转为系数g的球谐展开式系数，然后再将系数转换为待求的扰动位的球谐系数，下节将给出这些转换的计算公式。

在重力场模型求解中EHA-CT方法会有不同的实现形式，如果利用数值积分方法进行椭球谐分析，则该实现形式称为EHA-CT方法的积分形式；如果使用最小二乘方法进行椭球谐分析，则称为EHA-CT方法的最小二乘形式。而且模型求解时使用的离散的重力异常观测数据可以是格网点值数据或者格网平均值数据，针对不同的离散重力数据，EHA-CT方法也有不同的计算公式，2.1.1节和2.1.2节将给出这些计算公式。

2.1.1. 积分形式的EHA-CT方法

根据面球谐函数的正交性，由式（3）可以推导出使用椭球面重力异常数据计算系数的公式：

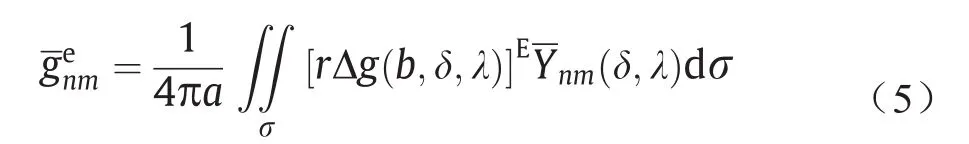
式中，文献[30]中有Λnmk的计算方法。

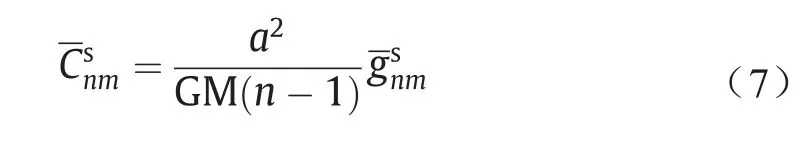
式中，GM为地球引力常数。

将式（5）和式（6）代入式（7）可得：

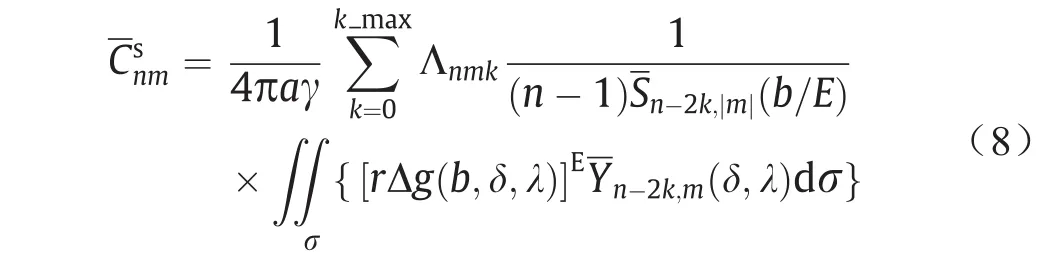
式中，γ=GM/a2。

虽然式（8）是严密的，但该式中的数据为参考椭球面连续的重力异常数据，而重力场模型解算可使用的数据一般为离散重力数据，所以该式不能直接用于重力场模型求解，需要把它离散化。针对不同形式的离散数据，式（8）有不同的离散化形式，有等角格网离散点值数据的离散化形式，也有等角格网离散平均值数据的形式。

如果离散数据为等角格网的重力异常平均值，式（8）的离散化形式为：

式中，i和j表示数据位于椭球面上的第i (i = 0, …, N-1)个纬度带和第j (j = 0, …, 2N-1)个子午带，这样的全球等角格网共有N行和2N列，i_max=N-1, j_max=2N-1；[ri]E为椭球面上第i个纬度带上格网中心的地心向径；为格网平均重力异常值是格网内[rΔg]E的平均值；是勒让德函数的积分和的计算公式为Appendix A中有该式更为详细的推导。

如果离散数据为等角格网的重力异常点值数据，式（8）的离散化形式为：

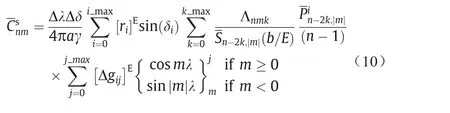
尽管式（11）中引入了平滑因子，但由于勒让德函数的正交性问题并未完全解决，计算得到的系数仍然有离散化误差，当前没有阅读到相关文献中有这个问题的解决办法，本文将在第3节中分析该离散化误差的大小。

然而，针对格网点值，可采用特殊的采样和赋权方法解决数据离散化中的勒让德函数正交性问题，如Gauss-Legendre (GL) [50]积分方法和Driscoll/Healy (DH)[36]积分方法等，本文将该方法引入到基于离散重力异常点值估计模型位系数。根据DH方法，可将椭球面划分为[N×N] (nmax= N/2-1)的格网，其中，nmax为待求系数的最高阶，纬度方向的格网间隔为Δδ = 180°/N，经度方向的格网间隔为Δλ = 360°/N；也可划分为Δδ = Δλ =180°/N的等角格网。DH方法定义数据的权为：

将式（12）中的权因子代入到式（10），可得椭球面点值数据计算系数的公式为：

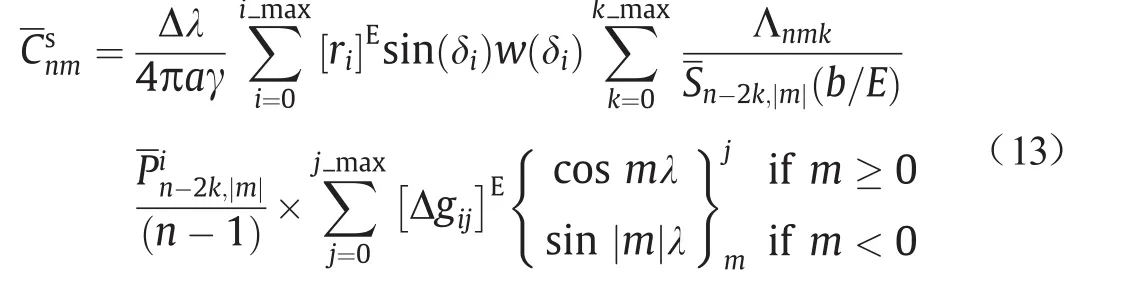
与DH方法类似，GL方法同样通过定义特殊的格网划分方式和权因子来解决勒让德函数的正交性问题[50]。GL方法中定义的格网是不规则的格网，纬度方向上格网的采样间隔相等，经度方向上的采样点为Pn|m|函数的零值点。Hirt等[51]使用GL方法对卷积积分进行数值分析，文献[50,51]中有GL方法的格网划分和赋权方法的详细介绍。

使用式（11）和式（13），可以分别由椭球面格网重力异常均值和点值计算重力场模型系数。Rapp和Pavlis [33]中的式（20）也是使用椭球面重力异常均值数据计算系数的公式，其推导方法与本文的式（11）相同，然而式（11）和文献[33]中的式（20）略有不同，其差异体现在本文推导式（11）和文献[33]中的一项因子分别为1/(n-1)和1/(n-2k-1)。从上文的推导可知，该差异项表征了系数和系数之间的关系，而从式（7）可知，这两个系数只与n有关。该项的差异会对系数求解产生影响，本文将在第3节分析该影响的大小。

2.1.2. EHA-CT方法的最小二乘计算公式

其中

根据式（14），在Gauss-Markov模型下，使用椭球面数据的函数模型和随机模型为：

同时，将式（6）和式（7）代入式（14）中，可以得到椭球面重力异常均值和点值数据与系数Cnsm的关系：

根据式（17）可以使用系数计算参考椭球面的重力异常均值和点值数据，同样可以使用该式由椭球面重力异常数据建立求解系数的观测方程。

EGM2008的计算中也使用了最小二乘形式的EHACT方法[18]，计算策略如下：

对比式（4）和式（18）可知，该策略与本文使用最小二乘方法的策略不同，如式（18）所示，Pavlis等[18]使用最小二乘方法首先求得系数，然后再使用Jekeli系数转换将系数转换为系数。

2.2. 重力异常数据和卫星重力数据的联合求解方法

本文使用最小二乘方法联合多类的重力数据，如重力异常数据、GOCE卫星数据和GRACE卫星数据求解重力场模型。在最小二乘方法中，当多类数据不相关时，使用最小二乘方法联合多类数据得到的联合解为：

式中，Ai为根据第i类数据建立的设计矩阵，它表征了待求参数与第i类数据之间的关系；Pi为数据i的权阵；li是观测数据向量；是数据i的初始方差分量；Ni和Ui是数据的法方程矩阵和法方程向量；是数据i的初始相对权。

由于联合不同法方程时使用的初始方差分量一般不准确，本文在联合多个法方程时使用方差分量估计方法（variance component estimation method, VCE）[53]通过迭代估计数据的方差分量，并在迭代的过程中求解得到多个法方程的联合解。在VCE方法中，方差分量的计算公式为[53]：

式中，k表示第k次迭代；vk,i为残差向量；rk,i为冗余度；文献[53]中有更为详尽的计算公式。

然而，在使用VCE方法联合多个法方程时会遇到一些问题。一方面，如果使用的法方程非自主构建时，法方程的提供者有时不能同时提供残差的加权和，这时就不能直接使用式（20）计算方差分量；另一方面，如果这些法方程的误差随机模型不同且不能准确建模时，VCE方法不能得到最优解[54]。Jean等[55]等提出了改进的VCE方法，在使用VCE方法时规避了直接使用观测值残差计算方差分量，而是根据每个法方程的解相对联合解的“误差”计算每个法方程的方差分量，计算公式如下[55]：

这样在每次迭代过程中，可以根据此次迭代的联合解，解算每个法方程的方差分量，并用于下一次迭代，直到迭代收敛并解得最终的联合解。

解算SGG-UGM-1模型时，由于重力异常数据法方程和卫星重力数据法方程的待求参数均为重力场模型的球谐系数，将这些法方程加权求和即可得到不同数据的联合观测法方程。然而求解SGG-UGM-2模型时，重力异常数据法方程的待求参数为椭球谐系数，卫星重力数据法方程的参数为球谐系数在联合这些法方程之前首先应把法方程的参数统一。本文在法方程联合之前，将参数为球谐系数的卫星观测法方程转换为参数为椭球谐系数的法方程。

式中，下标“s”表示相应的参量为卫星观测数据的参量；x^s为待求系数向量。

式中，Tse为根据式（6）和式（7）计算的系数转换矩阵；x^e为系数向量。

将式（23）代入式（22）中，可得：

在最小二乘准则下，可得式（24）的法方程为：

分析式（25）可知，该式给出了不同参数形式的法方程之间的关系，因此可以使用该式将参数为球谐系数的卫星观测法方程转换为参数为椭球谐系数的法方程，这样将法方程的参数形式统一后，再将这些法方程加权求和即可得到联合观测法方程。

3. EHA-CT方法计算公式的检验

本节的主要目的是通过数值试验检验第2节推导的计算公式。一方面，这可以保证用于SGG-UGM-2模型求解的计算公式是严密的；另一方面，2.1.1节的分析表明本文推导的由椭球面重力异常均值计算系数的公式与Rapp和Pavlis [33]的相应公式存在差异，通过数值试验可以验证公式的严密性，并分析该差异对求解系数的影响，为研究人员选择合适的公式计算重力场模型。

首先，使用重力异常均值数据通过式（11）计算得到一个重力场模型，称为Model1。图1中的红色曲线展示了Model1相对EGM2008模型的系数阶误差。2.1.1节的分析表明，尽管式（11）中引入了平滑因子，该式计算的系数仍有离散化误差，图1中Model1的误差反映了离散化误差的大小，该项误差对模型系数的影响最大可达10-11量级，这个误差在模型解算中不可忽略。除特殊说明外，本文中模型的系数误差均为绝对误差。

然后，使用重力异常点值数据分别通过式（13）和式（10）计算了模型Model2和Model3，式（13）和式（10）的区别在于是否使用DH权因子。模型Model2和Model3的系数阶误差分别为图1中的蓝色和深灰色曲线。由图1可知，模型Model2全频段的系数阶误差均小于10-17量级，可以认为该误差是计算机截断误差引起的。模型Model3的系数阶误差相对较大，而且在奇数阶和偶数阶之间有很大的波动。模型Model3的误差远大于模型Model1和Model2。结果说明式（13）是严密的，可用于模型反演，同时也说明，本文采用DH权因子有效解决了积分离散化后勒让德函数的正交性问题。

同时，使用模拟的重力异常点值数据，通过2.1.2节中的最小二乘方法计算了模型Model4，具体步骤为：首先，建立了式（14）所示的观测方程，然后求解该观测方程得到了系数；然后使用式（6）和式（7）将系数转换为系数。求解系数时使用了BDLS方法和OpenMP [57]并行计算技术提高计算效率。模型Model4的系数阶误差RMS为图1中的品红色曲线，从图中可以看出Model4模型的误差很小，可以忽略，这充分表明EHA-CT方法最小二乘形式的公式是严密的，可以用于SGGG-UGM-2模型的求解。而且，相对于积分方法，最小二乘方法更方便地联合解算多类观测数据，因此本文将使用最小二乘方法求解SGG-UGM-2。此外，我们也按照计算Model4的方法，使用重力异常均值数据计算了相应的模型，得到了与点值数据一致的结果，在本文中未做展示。

由于本文推导的式（11）和文献[33]推导的式（20）均存在离散化误差，其对解算系数的影响和公式差异对求解系数的影响会混叠在一起，在数值模拟试验中很难分辨由式（11）估计系数的误差是来源于系数公式严密性的影响，还是来源于离散化的影响，因此很难以此检验公式的严密性。考虑到式（13）与式（11）类似，都是使用离散重力异常计算系数的公式，它们的区别在于式（13）中的数据为重力异常点值数据，它们有相同的因子项1/(n-1)。类似地，如果文献[33]中的式（20）是正确的，那么将式（13）中的1/(n-1)替换为1/(n-2k-1)，就可以得到与该式相对应的且采用了DH权的，由重力异常点值数据计算模型系数的公式：

式（16）的严密性可以反映其因子项1/(n-2k-1)的正确性，进而反映文献[33]中公式（20）中1/(n-2k-1)的正确性，这是本文严格检验该公式与本文公式严密性的思路。为此，我们使用式（26），由格网重力异常点值数据计算了模型Model5，Model5的阶误差RMS为图1中的绿色曲线。从图中可知，在低阶次部分，Model5的系数误差较大，在5阶附近可达10-9量级。低阶部分（小于50阶）的误差大于10-11，这个误差不可以忽略。因此可以推断文献[33]中式（20）的1/(n-2k-1)是不准确的。

为了进一步分析文献[33]中的式（20）的严密性，分别使用模型Model2和Model5计算了参考椭球面上的重力异常和大地水准面误差，表2给出了误差的统计结果，图2给出了其空间分布。由表2可知，模型Model5在2160阶的重力异常和大地水准面的误差分别为0.18 mGal (1 mGal = 1×10-5m·s-2)和11 cm，这远远大于Model2的误差。Model5在阶次100～2160频段的大地水准面误差的最大值为3.5 cm，在阶次200～2160频段的大地水准面误差最大值为1.9 cm；在阶次100～2160频段的重力异常误差的最大值为1.4 mGal，在阶次200～2160频段的重力异常误差最大值为1.2 mGal。由图2可知，Model5有较大且为系统性的大地水准面误差，而Model2的大地水准面误差远小于Model5。这些结果反映了式（26）中1/(n-2k-1)的影响不可忽略。

4. SGG-UGM-2高分辨率重力场模型的解算

本文联合卫星测高数据、卫星重力数据和重力异常数据计算了2190阶2160次的高分辨率重力场模型SGGUGM-2。本节将首先简要介绍不同重力数据（卫星重力和卫星测高）的处理策略，然后介绍多个法方程的联合解算策略。

4.1. 建立GOCE和GRACE卫星观测法方程

图1. 模型Model 1（红色）、Model 2（蓝色）、Model 3（深灰）、Model 4（品红）和Model 5（绿色）相对EGM2008的系数阶误差RMS。（a）从2阶到2160阶；（b）2阶到200阶。黑线是EGM2008模型系数的大小。

表2 模型Model2和Model5相对EGM2008的重力异常和大地水准面误差的统计结果

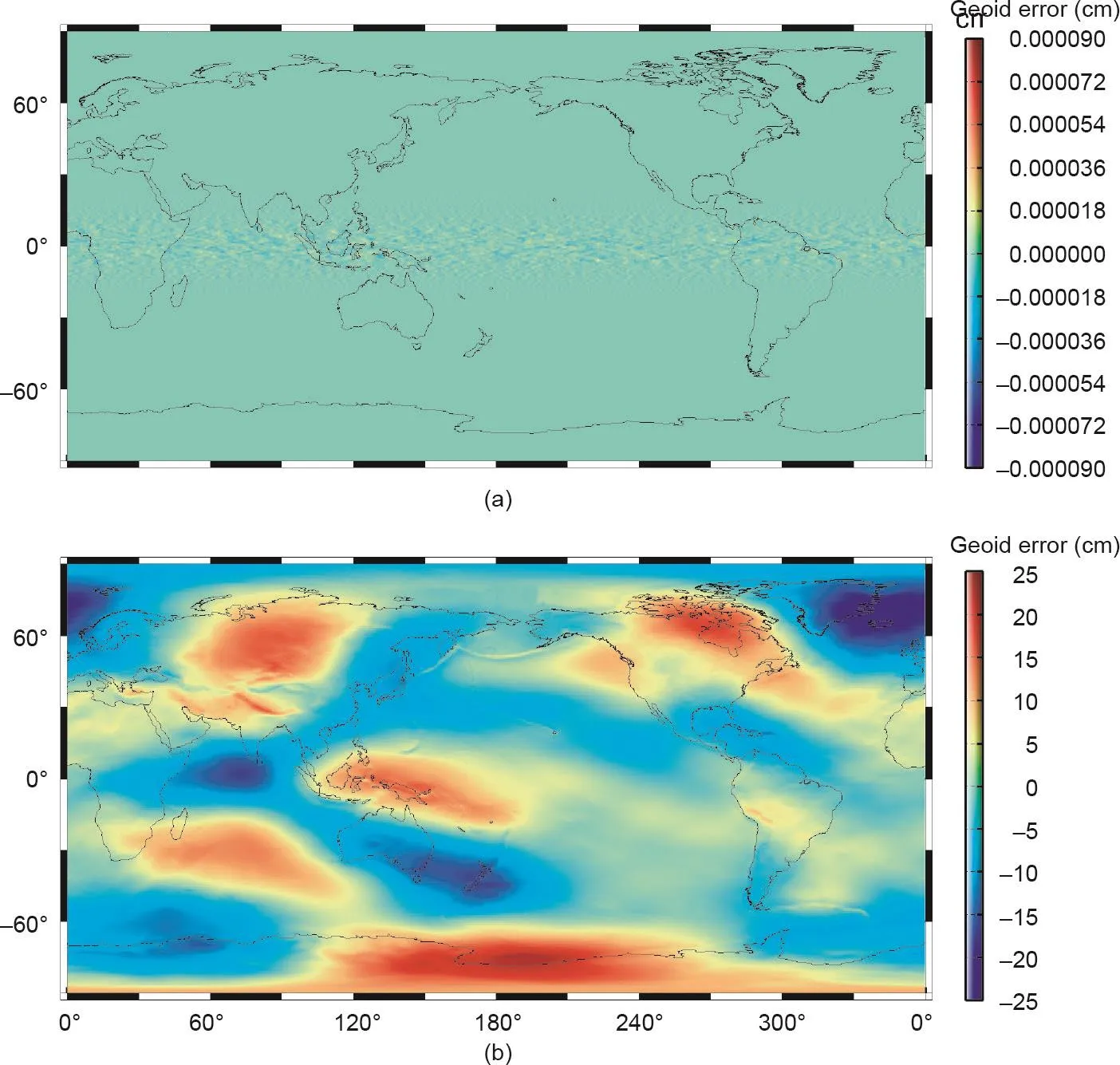
图2. 模型Model 2（a）和Model 5（b）的大地水准面误差的空间分布（2160阶）。

本文使用的GOCE卫星重力观测数据为2009年11月1日至2012年5月31日的EGG_NOM_2 (GGT, PRD,IAQ, PRM)数据和2009年11月1日至2010年7月5日的SST_PSO_2 (PKI, PCV, CCD)数据，数据的采样间隔为1 s [58]。EGG_NOM_2数据主要包含梯度仪坐标系（gradiometer reference frame, GRF）下的重力梯度张量数据（gravity gradient tensor, GGT），用于惯性参考系（inertial reference frame, IRF）和GRF坐标系转换的四元数数据EGG_IAQ_2，以及加速度数据EGG_CCD_2C。SST_PSO_2数据包含卫星运动学轨道SST_PKI_2（PKI轨道）、精密PKI轨道的方差-协方差信息SST_PCV_2、简化动力学轨道SST_PRD_2及地球固定参考系（earth-fixed reference frame, EFRF）与IRF之间转换的四元数SST_PRM_2。

模型反演中仅使用了GGT数据中精度较高的对角线分量（Vxx, Vyy, Vzz）用于法方程的构建[24]。使用卫星重力梯度数据（satellite gravity gradient, SGG）和高低卫星跟踪数据（satellite-to-satellite in high-low mode, SST-hl）分别构建了法方程，两个法方程参数的最高阶分别为220和130。建立GOCE卫星观测法方程的主要解算策略如下。

（1）首先对SGG数据和SST-hl数据进行数据内插、粗差探测等预处理。

（2）使用直接法由SGG数据建立法方程[24]，其中在建立观测方程时进行了通带为5～41 mHz的ARMA(auto regressive moving-average)滤波[59]，以解决SGG数据的有色噪声问题。根据公式fmax=Nmax/Tr计算的通带近似最高频率为fmax= 41 mHz，其中Tr=5383 s，是卫星绕地球旋转一周的所用时间）[60]，Nmax= 220，是求解模型的最高阶。

（3）采用点域加速度方法建立GOCE卫星SST-hl法方程，求解SST法方程得到观测值残差[60-62]。卫星的加速度是根据卫星运动学轨道使用EDF5 (extended differentiation fi lter)方法计算的，其中采样间隔Δt = 5 s [62]。

（4）根据SGG观测法方程和SST-hl观测法方程的方差分量将两个法方程联合，文献[24]中有法方程联合的具体实现方法。

这是本文建立GOCE卫星观测法方程的简要介绍，该法方程也是纯GOCE卫星模型GOSG01S和高分辨率模型SGG-UGM-1计算中使用的法方程。文献[24]中有建立该法方程的数据处理方法和计算流程的详细介绍。

本文没有直接使用GRACE卫星的原始观测数据构建法方程，而是使用GRACE静态重力场模型ITSGGrace2018 [48]的法方程作为GRACE卫星观测法方程。ITSG-Grace2018模型的研制团队发布了SINEX [63]格式的法方程，本文将SINEX格式的法方程转换格式后，将其用于SGG-UGM-2的联合解算。

4.2. 全球海域重力异常的确定

本文使用Geosat、ERS-1、Envisat、T/P、Jason-1、CryoSat-2和SARAL/AltiKa等多颗卫星的测高数据恢复了全球海域重力异常[45]，表3给出了粗差剔除、低通滤波等预处理前后的卫星测高观测值数目。从卫星测高观测值中获取的大地水准面高和垂线偏差是计算海洋重力异常的重要起算数据，其中相邻观测值之间差分计算垂线偏差的过程可以有效抑制轨道径向误差及其他长波误差项。因此，无需进行交叉点平差，之前的数值测试表明该方法与大地水准面解算方法解算精度相当 [64]。

我们对表3所述的多颗卫星测高数据进行联合处理，获取垂线偏差信息，进而计算海域重力异常[45]。这些处理包括：首先采用两步拟合法对多个测高卫星的原始波形进行重跟踪处理[45]，并将沿轨观测值统一重采样至5 Hz，提高观测值的精度和有效观测值数量；然后顾及数据产品自带的路径延迟及地球物理环境改正项信息，获取沿轨海表面高度和梯度信息，基于EGM2008模型梯度和3倍标准差准则剔除粗差；顾及沿轨差分过程中会放大高频噪声，采用Parks-McClellan低通滤波器滤波得到梯度观测值；分别使用DOT2008A模型和EGM2008模型考虑海面地形效应和大地水准面长波信号，结合测高卫星地面轨迹处经向、纬向速度的近似计算公式，得到“移去”参考场贡献的沿轨残余垂线偏差信息，并计算格网点处的残余垂线偏差方向分量；根据拉普拉斯方程导出的重力异常与垂线偏差的关系，进一步计算得到格网化残余重力异常；最后，“恢复”EGM2008参考场的长波信号后就得到了全球1′×1′分辨率的海洋重力异常数据。

为了验证解算结果可靠性，采用美国国家地球物理数据中心（National Geophysical Data Center, NGDC）提供的船测重力数据进行精度分析，并基于水深信息将检核数据划分为浅水区、非浅水区和深水区三类，分别与DTU10、DTU13和SS V23.1进行对比，如表4所示。结果表明，本文计算的海洋重力异常数据精度是可靠的，在非浅水区和开阔海域精度与同期的DTU13 and SS V23.1模型相当，优于早期的DTU10模型。

4.3. GOCE和GRACE卫星观测法方程与重力异常观测法方程的联合解算

卫星重力观测数据和重力异常数据对重力场不同频段信号的敏感度不同，因此不同的数据适于解算重力场的频段也不相同，充分利用各类观测数据包含的重力场信号，将多类观测数据进行最优联合解算是高精度高分辨率重力场模型解算的关键。通常认为卫星重力对重力场中长波信号敏感，重力异常对高频及超高频信号敏感。本文采用法方程的联合解算实现多类观测数据的联合求解，解算中认为GRACE卫星重力数据、GOCE卫星观测数据和重力异常数据三类数据之间不相关。图3给出了卫星观测法方程和重力异常法方程的联合求解策略，该策略参考了EGM96 [26]和EIGEN系列[19]模型解算的法方程联合解算方法。

表3 恢复海域重力异常使用的卫星测高数据

表4 在典型区域使用NGDC船测重力数据对模型进行检核的结果（单位：mGal）

GRACE观测法方程、GOCE观测法方程和重力异常法方程中位系数参数的最高阶分别为200、220和2159。为提高计算效率，本文构建重力异常法方程时使用了BDLS方法，因此重力异常法方程是块对角形式的法方程。如图3所示，这些法方程的联合可以分为高阶次部分和低阶次部分，在高阶次部分，模型的251～2159阶¯系数是求解重力异常块对角形式法方程得到的；而在低阶次部分，模型的2～250阶¯系数是通过联合全阶次的卫星法方程和块对角形式的重力异常法方程得到的。250阶称为过渡阶，一般大于卫星法方程的最高阶，这样可以使系数及其误差在此处的变换较为平滑。假设模型的两部分的系数是不相关的，才能将模型分为两部分单独解算，当然，这样的假设会带来一些近似误差。选取合适的过渡阶会尽量减小该近似误差，一方面选取的阶次越高，通过多类观测数据联合求解得到的系数越多，但是低阶次部分的联合法方程的规模也会变大，相应的计算量也会增大；另一方面，过渡阶提高到一定的阶，阶次增大对模型的结果产生影响很小。考虑本研究使用的计算平台和计算精度的需要，本文选取的过渡阶为250阶。

图3. GRACE、GOCE和重力异常法方程的联合解算方法。

考虑到卫星观测数据求解的重力场低阶部分系数的精度高于重力异常数据求解的系数，低阶的联合观测法方程101阶以下部分仅使用了卫星法方程，没有使用重力异常法方程。这个阶次的选择是通过分析卫星模型ITSG-Grace2018、GOSG01S以及EGM2008模型的大地水准面误差得到的，EGM2008反映了由重力异常数据解算的系数精度。如图4所示，EGM2008的大地水准面误差在100阶以下的误差均大于GOSG01S模型，在20～100阶的误差大于ITSG-Grace2018，从100阶开始它们误差的差异开始减小，所以认为EGM2008在100阶以内的表现较差。由于本文使用的陆地重力异常数据是由EGM2008计算得到的，因此认为重力异常求解的系数精度与EGM2008的特性一致，所以重力异常法方程没有用于构建联合法方程的2～100阶部分，而是用于构建联合法方程的101～250阶部分。

4.4. SGG-UGM-2模型的解算流程

图5给出了SGG-UGM-2模型的具体解算流程，模型解算中每一步的计算过程如下。

（1）根据4.1节的处理策略，使用GOCE卫星的SGG和SST-hl观测数据建立了220阶次的GOCE卫星观测法方程，法方程的参数为系数。同时，解算该法方程得到纯GOCE模型GOSG01S。ITSG-Grace2018模型法方程的原始格式为SINEX格式，对其进行格式转换，转换后的格式与GOCE法方程一致。

（2）使用2.2节介绍的法方程参数转换方法，将步骤（1）中构建的两个法方程转换为参数是椭球谐系数的法方程。

（3）根据4.2节中的海洋重力异常数据求解方法，使用多颗测高卫星的数据解算了5′×5′分辨率的海洋重力异常数据。

（4）根据式（27），使用EGM2008模型计算了参考椭球面上5′×5′分辨率的陆地重力异常点值数据，其中，GM和a参数分别 为3.986 004 415×1014m3·s-2和6 378 136.3 m，这与卫星法方程中相应参数一致。将步骤（3）计算的海洋重力异常数据和EGM2008计算的陆地重力异常数据融合得到全球重力异常数据，命名为ΔgF[65]。

图4. EGM2008、GOSG01S和ITSG-Grace2018模型的大地水准面阶误差。

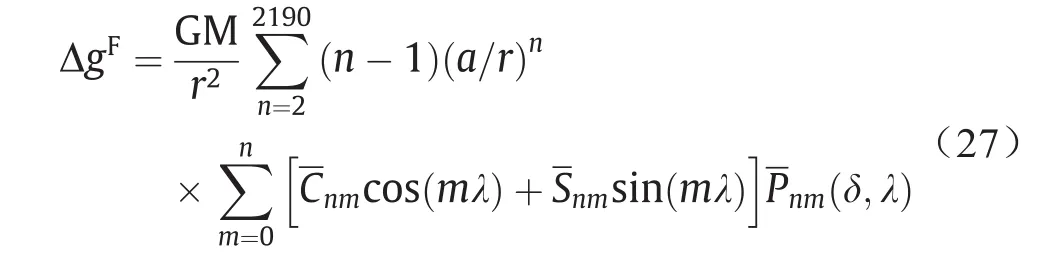
（5）由数据ΔgF使用块对角最小二乘方法构建2～2159阶系数块对角形式的法方程，在计算中引入OpenMP并行计算技术提高计算效率，同时求解该块对角法方程得到一组2～2159阶的系数。为满足块对角最小二乘方法的要求，用单位阵作为数据的权阵；根据EGM2008模型在2190阶的大地水准面累积误差，选取(5 mGal)2为法方程的初始方差分量。

（8）按照步骤（7）所述方法求得低阶次部分的系数后，使用2.2节中的VCE方法更新各个法方程的相对权。然后使用新的相对权对步骤（7）和步骤（8）进行迭代计算，直到法方程的相对权收敛。在SGG-UGM-2的计算中，最终进行了4次迭代，最终得到的重力异常数据、GOCE数据和GRACE数据法方程的相对权分别为1.0、1.9和1.3。

（10）使用式（6）和式（7）将步骤（9）中得到的2～2159阶椭球谐系数转换为2～2190阶0～2159次的球谐系数系数为扰动位的球谐系数，加上GRS80椭球的正常位系数后就可以得到最终解算的SGG-UGM-2模型系数。

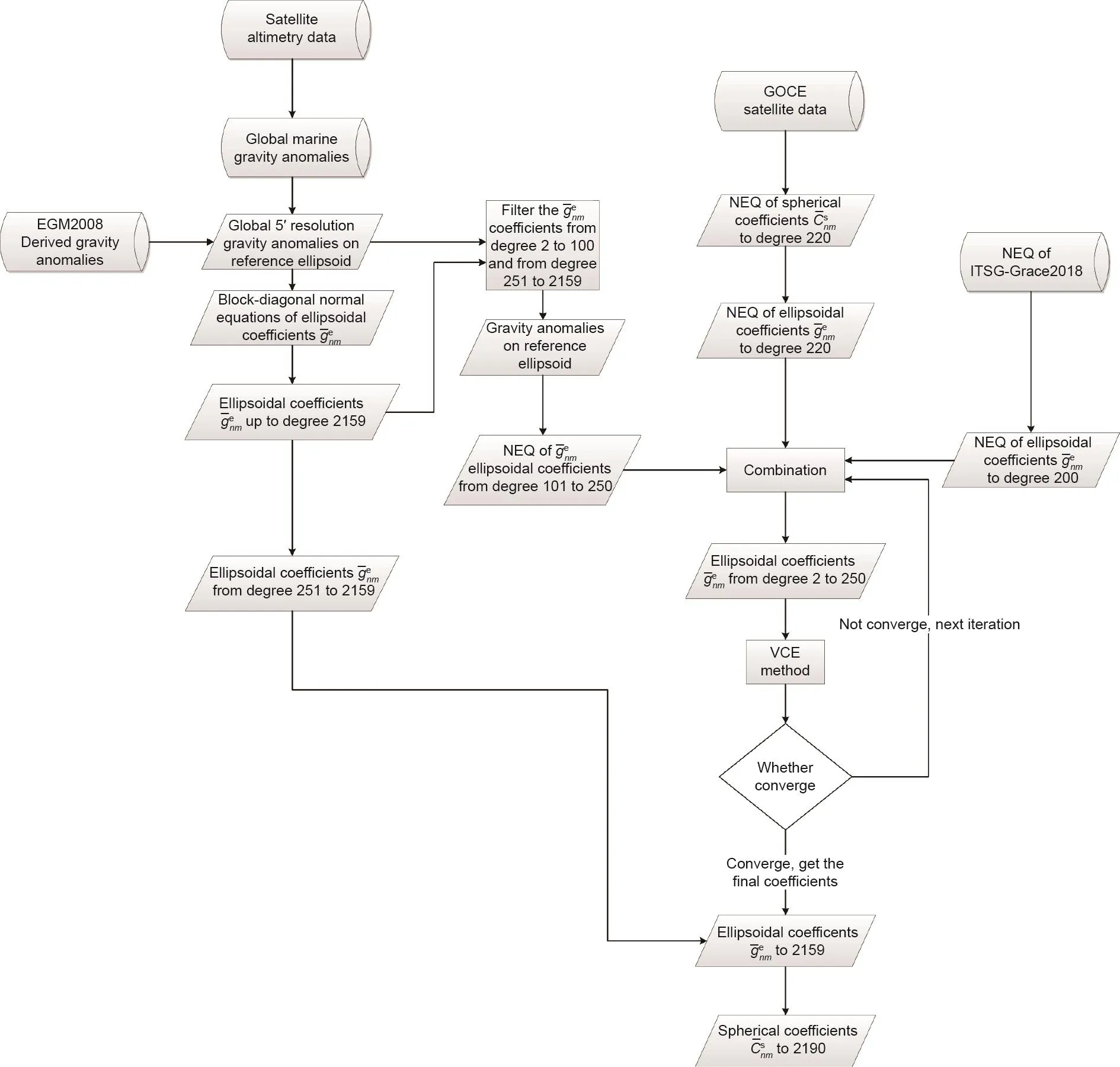
图5. SGG-UGM-2模型的计算流程。

5. SGG-UGM-2模型的精度分析

5.1. 与EGM2008在频域和空域的对比

为了分析SGG-UGM-2模型系数的精度，首先计算了它与EGM2008的系数差异，图6中的红色曲线为差异的阶RMS，图6也给出了另外两个高分辨率模型EIGEN-6C4和GECO与EGM2008的差异，图7给出了模型SGG-UGM-2、EIGEN-6C4和GECO与EGM2008系数阶差异的谱图。由图6和图7可知，在160阶以下，这3个模型与EGM2008的差异非常接近，尤其是SGG-UGM-2和EIGEN-6C4，这是由于这3个模型都使用了GOCE卫星数据。从160阶开始，这些模型的差异开始变大，这是由于这些模型使用了不同的重力异常数据和不同的数据联合解算方法。本文使用的海域重力异常数据是自主计算的，而GECO使用的是EGM2008格网重力异常，EIGEN-6C4使用的重力异常也与EGM2008重力异常接近，因此相较SGG-UGM-2，EIGEN-6C4在360阶以上的系数与EGM2008更为接近，GECO模型360阶以上的系数与EGM2008几乎一致。

图6. 模型SGG-UGM-2、EIGEN-6C4和GECO与EGM2008的系数阶差异RMS。

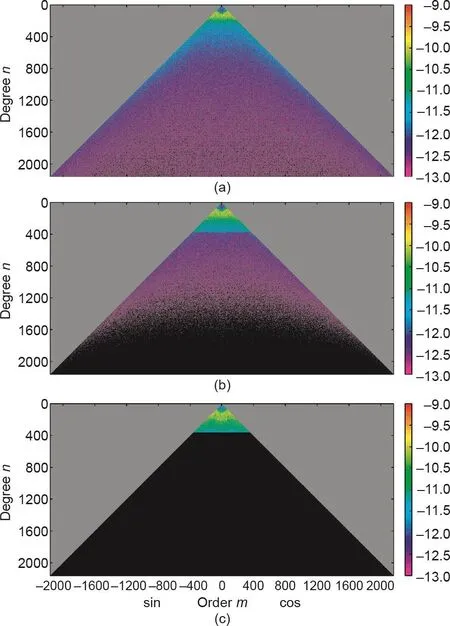
图7. 模型SGG-UGM-2 (a)、EIGEN-6C4 (b)和GECO (c)与EGM2008的系数阶差异谱图。

此外，使用SGG-UGM-2计算了全球重力异常数据，并计算了它与EGM2008模型重力异常和EIGEN-6C4重力异常的差异，差异的空间分布如图8所示，可知SGGUGM-2与EGM2008差异主要体现在青藏高原、南美洲、非洲中部等区域，这些区域的重力异常数据都很稀少，SGG-UGM-2与EIGEN-6C4在这些区域的差异相对较小，这反映了GOCE数据对SGG-UGM-2与EIGEN-6C4的贡献，GOCE数据改善了这两个模型在重力稀疏区域的精度。除这些区域之外，SGG-UGM-2与其他两个模型在沿海区域的差异也较大，造成该差异的原因是SGG-UGM-2解算中使用了与其他两个模型不同的海域重力异常数据。

5.2. 中国和美国的GPS/水准数据的检核结果

首先使用了中国大陆区域的649个GPS/水准点[66]和美国区域的6169个水准点[67]检验了SGG-UGM-2模型的精度，需要说明的是，中国区域GPS/水准数据的高程基准是正常高，美国区域GPS/水准数据的高程系统为正高。使用SGG-UGM-2、SGG-UGM-1、EGM2008、GECO和EIGEN-6C4模型计算了中国区域的似大地水准面高和美国区域的大地水准面高，通过与GPS/水准数据对比，计算模型的（似）大地水准面误差，计算中使用的潮汐均为无潮汐系统[67-69]。He等[69]的分析表明美国区域的GPS/水准数据在东西方向有约70 cm的倾斜，而中国区域数据在东西方向的倾斜为9 cm。表5和表6给出了模型的（似）大地水准面高在美国区域和中国区域误差的统计结果，在美国区域和中国区域误差的直方图分别为图9和图10，这些差异没有进行任何的改正。

根据表5、表6、图9和图10，通过分析模型误差的STD可知，在美国，EGM2008、SGG-UGM-1、SGG-UGM-2、GECO和EIGEN-6C4等模型的精度非常接近，模型误差STD之间的差异小于7 mm，这些模型误差的直方图的分布形态也很接近，展示了较大误差离散度，这可能是因为美国的GPS/水准数据在不同区域的质量不一致引起的。SGG-UGM-2在美国的精度最好，误差的STD为0.277 m，而EGM2008的精度最差，误差的STD为0.284 m。然而，这些模型在中国区域的检核结果差异较大，模型误差STD不尽相同，STD为0.157～0.240 m。使用了GOCE数据的SGG-UGM-1、SGG-UGM-2、GECO和EIGEN-6C4模型的精度较为接近，EIGEN-6C4的检核结果最好，它的误差STD为0.157 m，而EGM2008的检核结果最差，它的误差STD为0.240 m。从图10可以看出，使用了GOCE数据的模型在中国的误差直方图也相对接近，EGM2008误差直方图的离散度最高，它的特性与其他几个模型明显不同，这可能是因为EGM2008构建中使用GOCE观测数据，且使用中国区域的重力数据较为稀疏，而其他几个模型通过使用GOCE卫星数据提高了模型长波系数的精度，改善了模型在中国的精度，所以这些模型在中国区域的精度优于EGM2008。另外，SGG-UGM-1和SGG-UGM-2模型在中国和美国的检核结果都较为理想。同时，对比这两个模型可知，由于SGG-UGM-2中使用了最新的GRACE卫星法方程和海域重力异常数据，它在美国和中国区域的精度都优于SGG-UGM-1。EIGEN-6C4和SGG-UGM-2使用的观测数据和模型解算方法比较接近，所以它们在两个区域的精度也比较接近。两者的不同之处在于，EIGEN-6C4使用了更多的卫星重力数据，如LAGEOS卫星数据，以及采用了不同于本文的海洋重力异常数据；SGG-UGM-2解算中各类数据的相对权是使用VCE方法计算的，而EIGEN-6C4使用的相对权是通过经验方法确定的[12,19]。

图8. SGG-UGM-2模型重力异常与EGM2008 (a)和EIGEN-6C4 (b)重力异常差异的空间分布。

表5 模型大地水准面与美国GPS/水准数据差异的统计结果（6169个点）（单位：m）

表6 模型似大地水准面与中国GPS/水准数据差异的统计结果（649个点）（单位：m）

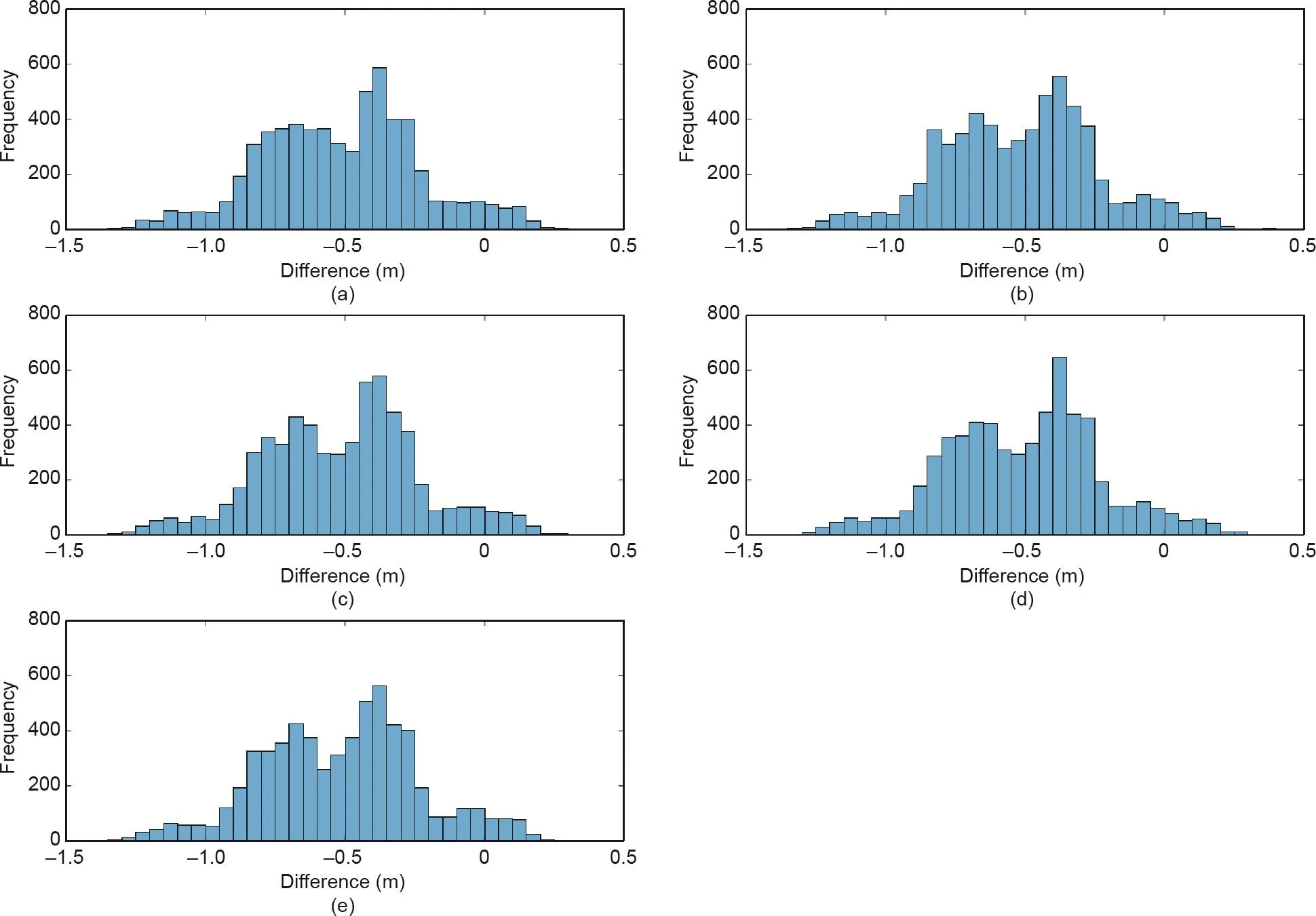
图9. EGM2008 (a)、 EIGEN-6C4 (b)、SGG-UGM-1 (c)、SGG-UGM-2 (d)和GECO (e)模型与美国区域GPS/水准数据差异的直方图。

同时，本文也使用了这些模型大地水准面误差的变异函数检核模型精度，模型误差的变异函数反映了模型误差方差与GPS/水准点间距离的关系。本文使用了文献[70]中经验变异函数的计算方法，通过文献[71,72]可知，“gammavariance” (GVR)代表了在给定的距离上模型误差的方差。图11给出了模型在中国和美国区域误差的经验变异函数。在中国区域，EGM2008和GECO的经验变异函数与其余3个模型有明显的差异，其在中国的GVR都较大。SGG-UGM-1、SGG-UGM-2和EIGEN-6C4在两个区域的GVR都接近。此外，在3000 km距离上，EIGEN-6C4模型在美国和中国的GVR均最小，这在一定程度上说明它在该波段的系数精度最优。

5.3. 青岛和台湾的GPS/水准数据的检验结果

为了检验模型在沿海区域和海岛的精度，使用了中国青岛和中国台湾两个区域的GPS/水准数据对模型进行检验，这两个区域都是沿海区域。青岛和台湾的GPS/水准数据中分别有152个点和88个点。表7和表8给出了模型在青岛和台湾的GPS/水准检验的结果，图12和图13是在青岛和台湾区域模型大地水准面误差的直方图，图14是模型在这两个区域误差的经验变异函数。青岛和台湾的GPS/水准数据的高程系统分别为正常高系统和正高系统，所以分别计算了模型在两个区域的似大地水准面高和大地水准面高。

由表7和表8可知，在青岛区域SGG-UGM-2模型误差的STD小于SGG-UGM-1，但在台湾区域却大于SGGUGM-1。一方面，青岛区域的结果表明SGG-UGM-2中使用了新的海洋重力异常数据提升了其在沿海区域的精度；但台湾区域的精度却没有提高，这可能是由于SGUGM-1和SGG-UGM-2使用的陆地重力异常是EGM2008计算的，而EGM2008模型构建时使用了台湾区域的精度很好的地面重力数据，新的卫星重力数据和海域重力数据不能进一步提高其在台湾的精度，这也造成了SGG-UGM-1、EIGEN-6C4和GECO在台湾的精度均不如EGM2008。在青岛，这些模型误差的直方图比较接近，这与表7中的统计结果一致。而在台湾这些模型的直方图有明显的不同，这是由于台湾的地形较为复杂造成的。与表7和表8类似，在图14中，EGM2008的经验变异函数最小，尤其是在80～140 km的空间分辨率上，近似对应于模型的140～250阶次，从采用了GOCE数据的超高阶重力场模型在海洋和美国本土的区域检验可以说明，这部分频段的主要贡献来自于地面重力数据，因此GOCE卫星重力和新导出的海洋重力异常对模型在台湾区域精度的提升无实质性贡献。

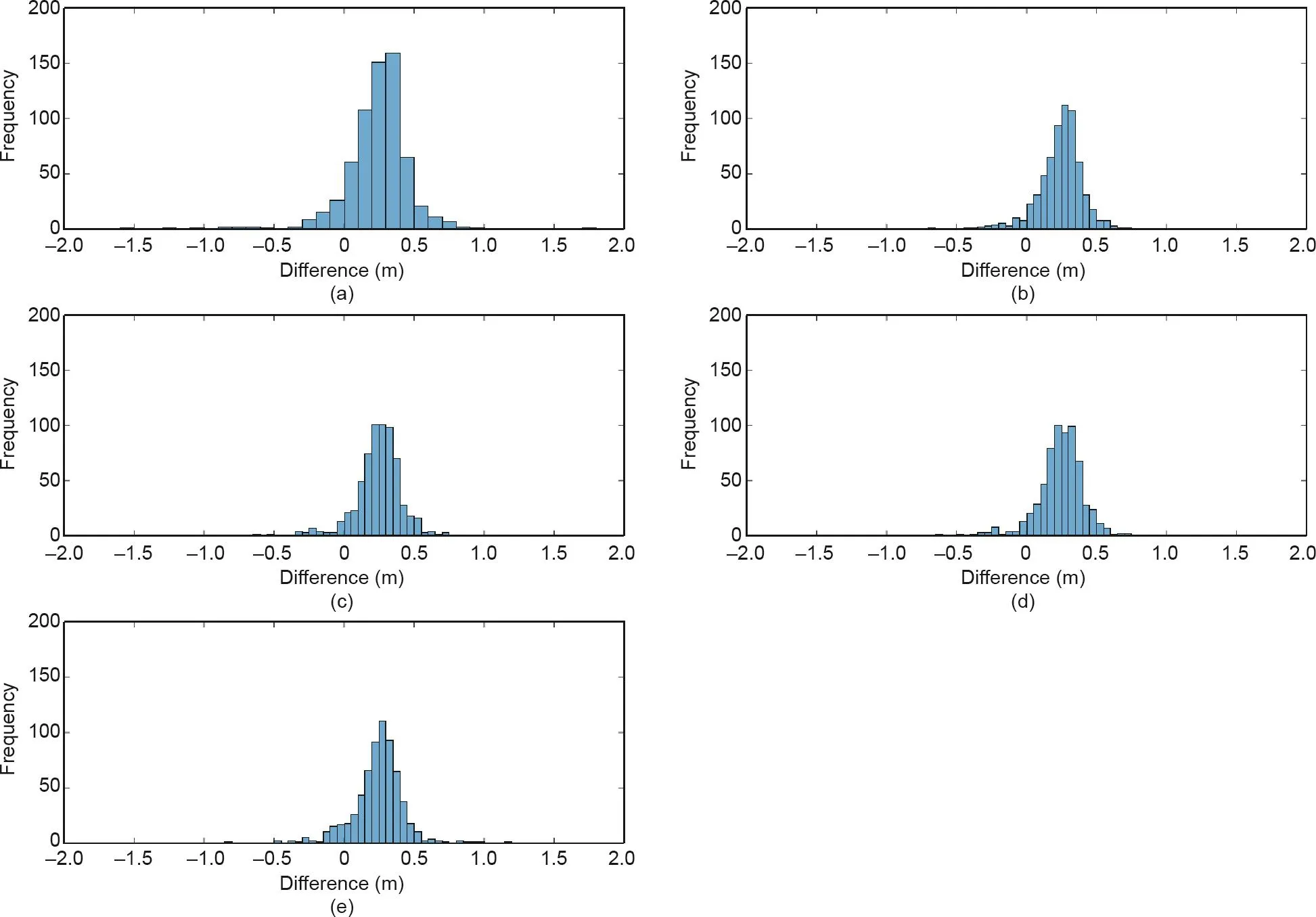
图10. EGM2008 (a)、 EIGEN-6C4 (b)、SGG-UGM-1 (c)、SGG-UGM-2 (d)和GECO (e)模型与中国区域GPS/水准数据差异的直方图。

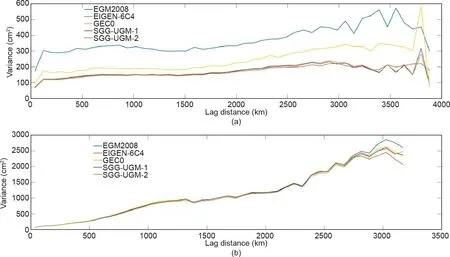
图11. EGM2008、EIGEN-6C4、GECO、SGG-UGM-1和SGG-UGM-2模型与中国（a）和美国（b）区域GPS/水准差异的经验变异函数。

表7 模型似大地水准面与青岛GPS/水准数据差异的统计结果（152个点）（单位：m）

表8 模型大地水准面与台湾GPS/水准数据差异的统计结果（88个点）（单位：m）

图12. EGM2008 (a)、 EIGEN-6C4 (b)、SGG-UGM-1 (c)、SGG-UGM-2 (d)和GECO (e)模型与青岛GPS/水准数据差异的直方图。

图13. EGM2008 (a)、 EIGEN-6C4 (b)、SGG-UGM-1 (c)、SGG-UGM-2 (d)和GECO (e)模型与台湾GPS/水准数据差异的直方图。

图14. EGM2008、EIGEN-6C4、GECO、SGG-UGM-1和SGG-UGM-2模型与青岛（a）和台湾（b）GPS/水准差异的经验变异函数。

6. 结论

本文深入研究了EHA-CT方法的基本原理，并给出了实用化解算策略；推导了根据EHA-CT方法使用椭球面重力异常均值数据和点值数据反演重力场模型的严密计算公式，在由椭球面点值计算重力场模型的公式中引入了DH采样和赋权理论[36]，数值试验结果表明，本文推导公式是严密的，可用于重力场模型的解算；对Rapp和Pavlis [33]实现EHA-CT方法的积分公式进行了验证，数值试验表明该式不正确，对重力场模型的中长波分量影响较大。

同时，联合GOCE卫星的SGG和SST-hl观测数据、ITSG-Grace2018模型的法方程、多代测高卫星数据和EGM2008重力异常数据解算了一个新的5′×5′分辨率的地球重力场模型SGG-UGM-2，模型完全展开到2190阶2159次。在频域和空域内与EGM2008的对比分析说明，SGG-UGM-2模型的精度可靠。中国和美国GPS/水准数据检核的模型大地水准面误差的统计结果、直方图和经验变异函数表明，在中国和美国区域SGG-UGM-2优于SGG-UGM-1、GECO和EGM2008模型，在美国区域SGG-UGM-2模型的精度最优。由于SGG-UGM-2模型解算中使用了新的GRACE法方程和新反演的海域重力异常数据，因此SGG-UGM-2模型在中国大陆和美国的精度均略优于SGG-UGM-1。这些结果均说明SGG-UGM-2模型精度是可靠的，可用于相关的地球科学研究和工程应用；同时，研究结果也表明解算SGG-UGM-2模型使用的方法是严密的，是后续研制和发布SGG-UGM系列高分辨率重力场模型的重要基础。

致谢

感谢Mayer-Gürr和Kvas提供ITSG-Grace2018模型的法方程。本研究获得国家自然科学基金创新研究群体项目（41721003）和面上项目（41574019、41774020）资助，并获德国DAAD主题网络项目（57421148）、高分辨率对地观测系统重大专项、中央高校基本科研业务费专项资金（N170103009）资助。我们也感谢编辑和匿名审稿人的建设性意见，帮助我们提高了稿件的质量。

Compliance with ethics guidelines

Wei Liang, Jiancheng Li, Xinyu Xu, Shengjun Zhang,and Yongqi Zhao declare that they have no con fl ict of interest or fi nancial con fl icts to disclose.

Appendix A. Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2020.05.008.