中国动态大地坐标框架最优实现的方法与应用

程鹏飞，成英燕,*，王晓明，吴素芹，徐彦田

a Chinese Academy of Surveying and Mapping, Beijing 100036, China

b Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China

c School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China

1. 引言

2000国家大地坐标系（CGCS2000）于2008年7月1日被正式公布为国家大地坐标系[1]。CGCS2000框架在2000.0历元（即参考历元）与国际地球参考框架（ITRF）97一致，框架包括2600个全球定位系统（GPS）大地测量控制点的坐标及速度[2,3]。为了从不同观测时间的GPS观测数据中获得GPS测站在CGCS2000框架中的精确坐标，通常需要两个主要步骤：①在ITRF中处理所有GNSS测站的观测数据，以获得高精度的坐标；②采用板块运动模型将这些测站在观测时刻的坐标归算到CGCS2000，即基于线性或非线性速度模型的高精度板块运动模型进行改正。

ITRF2014之前的各版本ITRF都是基于线性模型建立的，基于该模型可获得大地测量参考点的线性速度[4,5]。线性假设对区域构造解释具有重要意义，但由于测站运动的非线性特性，如果不顾及非线性运动，特别是在忽略荷载效应的情况下，测站位置残差可以达到几厘米量级。而全球针对海平面上升的研究需要一个精度为1 mm的地球参考系（TRF）[6]。此外，已有研究[7-9]表明，从许多GPS测站的坐标时间序列中检测到的季节性信号的振幅和相位随时间变化。这些周期性信号不会影响ITRF定义的参数，尤其是原点和比例尺[10]，尽管当测站观测时间少于2.5年时，其速度的估计可能会受这些因素的影响[11]。然而，对于位置有较大季节性变化的测站，估计周期信号将提高速度的精度，且有助于检测位置时间序列中的不连续性，从而改进序列中偏差值的确定。

ITRF2014是ITRF历史上第一次通过模型化测站非线性运动构建并发布的框架，包括测站位置的季节性（年和半年）信号以及易受大地震影响的测站震后变形，因此优于过去的ITRF版本。但是ITRF2014是建立在长期变化趋势为线性且季节信号振幅恒定的假设基础上的。虽然这一假设对于许多需要1 mm精度水平的TRF的研究具有重要的影响，但描述仍与现实中测站非恒定振幅和相位运动不符。为了解决这一问题，并进一步提高TRF的精度，本研究探讨了一种用奇异谱分析（SSA）方法建立的非线性运动模型。

本文概述如下。第2节介绍了GNSS测站坐标估计的数据处理策略，包括GNSS基准站选择标准、测站分区方案等。第3节介绍了不同模型的性能，包括基于线性速度假设的板块运动模型构建，以及从特定历元到2000.0历元的测站坐标改正。第4节介绍了本研究所提出的用于非线性运动建模的SSA方法，并比较了SSA方法与ITRF2014中非线性实现方法的效果。第5节给出了结论。

2. 数据处理策略

2.1. 全球基准站选取

为了获得最佳的CGCS2000，必须选择一组覆盖中国及其周边地区的GNSS基准站。备选基准站从位于欧亚板块的国际GNSS服务组织（IGS）基准站中选取。从中确定并选择满足以下3个标准的基准站作为初选站：①基准站速度分量的中误差小于3 mm·a-1；②基准站远离板块构造变形带；③对基准站至少连续观测5年。根据这些标准，选择了1999—2009年有10年观测数据的测站，共126个作为初选站。然后按以下标准进行进一步检验：①同一板块内所有初选站的速度分量与该板块的运动趋势大致相同，并且量级相同；②所有初选站在地理上分布均匀。具体选择步骤如下。

第一步：利用最小二乘法估计出两组速度之间的7个转换参数。一组速度来自NNR-NUVEL-1A模型，另一组为测量的速度，即ITRF2005框架[12]内所有初选站在GNSS数据处理过程中估计的速度。剔除速度残差大于2倍中误差（视为粗差）的测站。

第二步：确定并剔除测站的速度和方位角远大于其平均值的测站。这一判定是基于刚性板块上所有初选站的速度和运动方向的大小没有显著差异的假设，即它们在空间中缓慢变化[13]。识别步骤如下。

首先，将每个初选站在x、y、z分量上的测量速度(Vx, Vy, Vz)和模型（如NNR-NUVEL-1A模型）计算速度(Vx,Vy, Vz)model转换成站心坐标系的水平分量。水平速度矢量V = (Ve, Vn)（Ve、Vn分别表示沿东方向和北方向的速度）由下式获得：

式中，φ、λ分别是测站的纬度和经度。

其次，由初选站的水平速度矢量，通过式（2）采用最小二乘方法计算得到每个板块的欧拉矢量(Ωx, Ωy, Ωz)：

式中，r是测站到地心的距离。

获得欧拉矢量后，可由式（2）计算测站的速度，并称其为模型速度。根据下面的式（3）计算的速度方位角是模型方位角，分别用Vplate_model和Λplate_model表示。然后将模型速度和方位角与同一测站的实测速度和方位角(V, Λ)进行比较。

如果速度或方位角的差值大于2倍中误差[式（4）]，则剔除该测站。式（4）中，σ1为所有初选站的板块模型计算速度与实测速度拟合的标准差；σ2为方位角拟合的标准差。

第三步：在整个板块上选择分布比较好的测站。在实际应用中，初选站的分布通常并不均匀。这一步将排除位于密集区域且精度较低的测站。我们采用栅格化方法来识别这类测站。该方法的两个原则：①所选测站的覆盖面积尽可能大；②所选测站的分布尽可能均匀。

具体的选站过程包括3个步骤：①根据经纬度将每个板块划分为多个网格；②计算每个网格中的测站数，并计算所有网格中测站数的平均值；③采用式（4）识别并排除精度较低的测站，并对测站数量大于步骤②中获得的网格平均值的测站进行筛选。事实上，过滤的标准可以简单地基于式（3）。

按上述标准选取后，最终从126个初选站中选出92个IGS站作为GNSS数据处理的控制站。

2.2. 间距分区法

目前国际上高精度GNSS数据处理软件，如GAMIT或Bernese，在处理大型GNSS测站网数据时站数受限；如果测站数多于50个，其处理效率会迅速下降。因此，将整个区域划分为几个区或分组是经常采用的解决方案。如前所述，在选择参考控制站时除了考虑基准站坐标精度外，还需要考虑两个基准站之间基线的长度。与常用的基于测站的地理位置分区方案不同，本文提出了一种新的分区方法：间距分区方法（partition spacing method, PSM），它是基于整个区域内的测站并行分组的。PSM的过程包括3个步骤：①将中国大陆分成分辨率为2.5° × 2.5°的网格，计算每个网格的所有测站的数量；②根据所处理测站的数量和软件可处理的测站数限制确定分区的数目；③将每个网格中密集分布的测站分配到不同的区。图1为分区示例，其中左上图为所有测站的分布图，其他3个图为使用PSM划分的3个区的分布图。

此方法已成功用于国家GNSS连续运行基准站（CORS）网的日常数据处理。分布在全国的210个CORS被分为5个区。每个区包括分布在整个中国大陆的大约43个测站。

为了说明PSM相对于一般分区方法，如地理分区方法（GPM）在精度上的改进，将不分区的结果作为真值标准，并将其与采用PSM和GPM获得的结果进行对比，具体结果展示在图2和图3中。图2为基线相对精度，图 3为测站坐标的差异。从图中可以看出，基于PSM的基线相对精度明显优于GPM。此外，基于PSM得到的坐标差比基于GPM得到的坐标差更加均匀和稳定，利用PSM得到的水平和垂直方向上的坐标精度分别为1 mm和2 mm，而利用GPM得到的在水平和垂直方向上的坐标精度分别为2 mm和4 mm。

3. 板块运动模型构建与参考框架线性维护

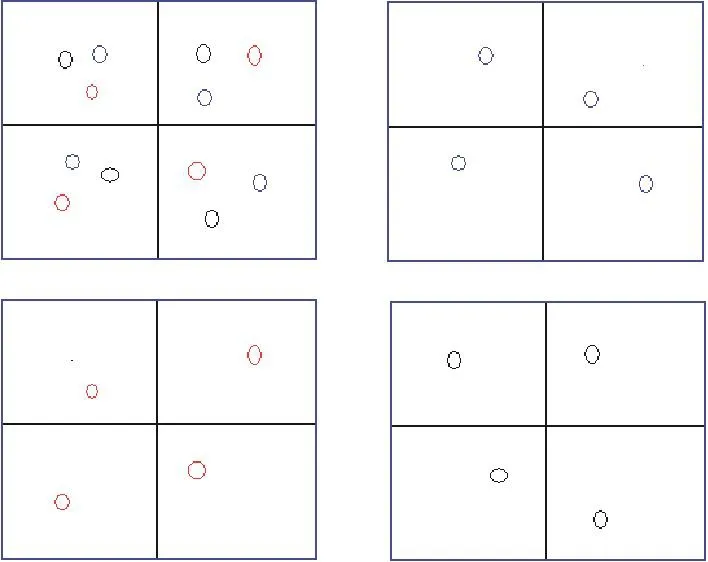
图1. PSM示意图（颜色只是便于理解）。

图2. 比较由PSM（红线）和GPM（蓝线）得出的基线相对精度。

图3. 比较PSM（红线）和GPM（蓝线）产生的坐标差，其中B、L、H分别代表经度、纬度和大地高。

常用的参考框架维护方法有两种：①使用改进的板块运动模型构建线性速度模型[14,15]；②构建非线性运动模型。第一种方法的优点是可以利用板块上所有基准站的速度来建立板块运动模型，可将任一测站任何历元下的坐标通过板块模型转换为特定框架特定历元下的坐标。然而，由于忽略了非线性运动，这种方法使得坐标归算精度只能达到厘米级。非线性速度模型可以达到毫米级的精度，但由于是基于特定测站建立的模型，不能扩展和用于其他测站。

许多学者开发了各种板块运动模型，如NNRNUVEL-1A、APKIM2005 [16-18]和PB2002 [19]。然而，这些全球模型在将GNSS测站坐标修正为CGCS2000时精度较低，因为上述模型在构建时没有加入足够的中国测站。

3.1. 速度场估计与板块模型构建

本文利用来自中国地壳运动观测网（Crustal Movement Observation Network, CMONOC）的10年的观测资料，共处理了1720个GNSS测站，包括34个CORS、56个基本站和1630个区域站。将整个中国大陆分为4个区，并使用GAMIT软件（10.35版）估算速度场并构建了中国大陆板块模型（CPM-CGCS2000）。

在10年的观测期间，一些基准站由于强烈地震、海啸等出现了测站的位置突跳。因此，对坐标时间序列进行分段并对分段速度进行估计，以保证所构建的刚性板块模型更稳定、更精确。

在92个国际参考基准控制下，获得ITRF2005框架的12个IGS站和23个国内基准站的坐标和速度，并由这些测站作为基准估计了国家基准网和区域网的1720个测站的位置和1072个测站的速度。

地震在中国区域频发。在选定的CORS的10年观测期间，至少发生了两次大地震，即2001年昆仑山地震和2008年汶川地震。此外，2004年印度尼西亚发生的海啸也对中国部分地区造成影响。基于中国CORS的坐标时间序列分析，发现部分测站受到这3次事件的影响，例如，一些测站位置发生了移动，事件发生后的运动速度的趋势也发生了变化。为了获得受影响区域的可靠速度场，根据事件发生的日期对这些基准站的观测时间序列进行分段，以便对不同时段的数据进行单独处理。

由表1可知，大部分测站的震前和震后的分段速度分量差异为3～5 mm∙a-1（如QION、XIAG、WUHN和HAIK站），同时导致速度矢量也发生了变化。因此，根据这些事件发生的时间，将时间序列（或GPS观测值）分成若干段进行速度估计，基于测站影响和时间段，根据稳定区域的速度场构建了板块运动模型CPMCGCS2000。

表1 时间序列分段的CORS

表2和表3分别给出了1072个基准站（包括CGCS2000中25个CORS、56个基本站和991个区域站）在水平方向和垂直方向上的速度场统计精度。可以看出，99%的速度场在水平方向上的精度小于0.5 mm∙a-1，而92%的垂直方向上的速度场精度小于1.0 mm∙a-1。

3.2. 板块运动模型CPM-CGCS2000

板块运动模型的精度取决于以下因素：①观测数据的数量和质量以及基准站的分布；②板块划分的合理性和确定的板块边界的准确性；③用于选择基准站的标准的合理性，为了符合刚性板块的假设需剔除位于变形区域的测站。参考文献[20]表明，当使用或不使用变形区域的观测站时，欧拉极位置的差异可能达到数10°，速度差异达到20%～30%。时间序列分段的目的是排除位于变形区或受严重自然灾害影响的测站，以得到真正反映板块运动的速度。

3.2.1. 中国板块划分

作为地质形成史上最复杂的地区之一，中国板块在板内构造和大陆动力学的研究中受到了世界各地许多科学家的极大关注[21-27]。中国大陆在不同时期被不同的研究者划分为不同的构造单元[28-38]。而目前最常用的划分来自于国家基础研究项目（973项目）的子项目“大陆强震机理与预测”，该项目将中国大陆及其邻近地区的活动块体分为一级和二级。我们只关注22个二级板块：拉萨、羌塘、巴彦喀拉、柴达木、祁连、川滇（四川-云南）、滇西（云南西部）、滇南（云南南部）、塔里木、天山、准噶尔、萨彦、阿尔泰、阿拉善、中蒙、中韩、鄂尔多斯、燕山、华北平原、鲁东-黄海、华南、南海板块。值得注意的是，在这些块体中，萨彦板块因为没有观测站，所以没有观测数据，而滇西和滇南的测站较少，所以将两块体合并为滇西南块体。因此，研究的二级板块的实际数量为20。

根据板块构造理论，地壳各板块的运动遵循欧拉定律，即Pi板块上j点的水平运动可以表示为：

式中，wi=(Ωx,Ωy,Ωz)为板块Pi的欧拉矢量；为j点的位置矢量。

基于式（5），在过去的10年里，许多研究者已经开发了几种板块运动模型。在本研究中，根据国家重点基础研究项目子项目的划分，初步确定了两个相邻板块之间的边界，并将用于建立板块运动模型的所有基准站按其坐标投影到与其关联的二级板块。对于每个二级板块，进行初始最小二乘平差，以获得板块中所有站点的速度。根据所有测站速度的大小和方向，特别是靠近初始边界测站的速度的大小和方向与板块整体的运动趋势是否合理，进一步调整初始边界的边缘线，并最终确定边界。为了建立可靠的板块运动模型，将位于明显变形区、板块边界附近或地震非常活跃的地区的测站视为不稳定测站，且其不参与板块拟合计算。此外，测站的分布会影响用于板块运动模型参数估计时法方程的强度。因此，我们选择了分布尽可能均匀且处于稳定区域的测站。为此，进一步识别其他不稳定测站的准则是：如果一个测站的速度值，即O-C（观测值减去计算值）大于最小二乘拟合结果的3倍中误差，则该测站的速度被视为异常值而剔除。在完成上述过滤程序后，从1025个初选站点中排除了17个测站。其余1008个被视为稳定且无显著异常值的测站，用于建立最终板块运动模型。拟合后华北平原、鲁东、燕山、鄂尔多斯、天山、中韩、中蒙、华南、阿拉善、阿尔泰、南海各板块上的速度拟合后残差约为2 mm∙a-1；祁连、川滇、塔里木、柴达木、羌塘、巴彦喀拉、滇西南板块的速度拟合后残差约为3～4 mm∙a-1。拉萨板块的扰动比西部其他板块大，因此反映运动的一致性较差。表4列出了20个板块的欧拉矢量及其拟合精度，从中可以看出，所建立的CPMCGCS2000中各板块的精度都很高。

表2 水平方向上速度场的统计精度

表3 垂直方向上速度场的统计精度

在表4中，λ和φ分别描述了板块旋转的极点的经度和纬度（十进制度数）；ω是板块的旋转速率，单位为 (° )·Ma-1（Ma为百万年）。表4第4栏为所有选定测站O-C值的均方根（RMS）统计值，结果表明，最佳、最差和平均均方根分别为0.31 mm∙a-1、5.02 mm∙a-1和1.62 mm∙a-1，这些结果表明，所建立的CPM-CGCS2000的速度数据适应性较好。

3.2.2. CPM-CGCS2000模型验证

表316 67.366 ± 27.72420403009838 3.34± 1.868 1.1924± 1.840± 17.75± 10.90± 1.533 5 ± 1.932± 6.153± 5.218762.5± 11± 2.612572.9354.2592.8 23.175 ± 7.2301 15.875 ±-4.763 57.897 ±-7.332 51.660 28.444 71.985-16.10 30.915 35.310 55.182 67.447 2.668 ± 0.6565± 0 83.524± 2± 1.4184± 1± 2.4174 φ (° )-168.323 68.067 72.717 63.438 332532620.79282841 37098 23.2 4.11 6.8425.7 0.1423 5.5482 3.38 9 ±4 ± 0.9223 2.79 6 ±0.71 9 ±69 ± 1 1 ± 0.718 10 ± 25.6094 2 ± 8.0158 03 ± 456.762 λ (° )-71.47-85.76-87.77-81.13.1-109-87.84.0-127-64.96 68.856 ± 7.8590.799 ±-15.475 ± 0.463-87.088 ± 1.978-88.648 ±-82.339 ±-7-1124.802 ±-8.1-222.856 ± 5.1557-121.589 ± 2.8718-130.585 ±-1-110.348 ±1)455 199 717 602198619031088670099 a-.5.2.20.0513.51.1150 0.57 0.16 ω ((° )∙M 0.399 ± 1 0.342 ± 0 0.419 ± 0.6453 0.616 ± 0 0.399 ±0.951 ± 0 0.321 ± 0.7263 0.428 ±0.399 ± 0.12 2 ± 0.85 0.95 2 ± 0.39 0.32 3 ± 0.3582 0.45 9 ±0.47 4 ±0.62 7 ± 0.07 0.49 9 ± 0.42 1.71 5 ± 0.13 0.36 0 ± 0.0755 0.35 7 ± 0.10 0.59 3 ± 0.1206 0.36 737615 009.0002.0009.0002.0002.0007.0001.0 a-1)± 0.002± 0.000± 0.000± 0.000± 0.000± 0.000± 0± 0.0007± 00.0002 0.0002 Ωz (rad·M 0.004746 0.001580 0.002678 0.000900 0.004548 0.002104 0.003626 0.003822 0.006133 08042 ± 0 17 ± 0.0005 61 ± 0.0002 57 ± 0.0009 37 ± 0 43 ± 0 92 ± 0 37 ± 0.0003 33 ± 0 14 ±47 ±.0-00.0029 0.0030 0.0040 0.0046 0.0022 0.0065 0.0047 0.0051 0.0055 0.0044 64 009-03 876 ± 0.002 542 ± 0.000± 0.0012± 0.0009 02695 ± 0.0002 0202.0021.0002.0011.0002.0 a-1)0.0012 0.0015 0.00 0.00 Ωy (rad·M 90 ± 0 65 ± 0.0007 8 ± 0.0007 1 ± 0.0001 3 ± 0.00-0.001-0.005 0.006253 0.010674 1582 ±2084 ±.016341 ± 0.006392 ±0.0022.000385 ± 0.027764 ±04319 ± 0.0007 02689 ± 0.001777 ± 0.009939 ± 0.0002-0.0048-0-0-0-0-0.0-0.0-0.0-0-0.00002 0.00 003--0.00176-0.00130 0.00 28 ± 0.0001-0 01 02 10 ± 0.0001 0101 002-0.00 0247 ± 0.0001-0.00 02 0.00 02 0.00 3 ± 0.0001.0 0.0000.0 0.00 42 ± 0 63 ± 0 1 ± 0.0002-0.0001 a-1)0.00 3 ±01 0.00 6 ±·M 03 86 ±3 ± 0.0001-0.0006 0.0004 00936 ±0.001616 ± 0.0002 0.00 2197 ±1)Ωx (rad 0.00020102 ±0856 ±0904 ±0748 ±.00.0006 01726 ± 0.0004-01957 ±0111-0.0-00.0029.0-00.00 0.00 0.00 0.00-0.00074 0.00 0.00-0.00102-0.00108.0-0-0.00077 m∙a-(m MS g R Fittin 0.74 0.82 2.02 1.76 1.67 3.39 2.38 5.02 0.69 2.48 1.94 1.50 1.29 0.88 1.76 0.31 0.98 0.88 0.98 0.81度No. of station 5 s 18496297933529391566913257425239580精173的块Sea板个20 ea和量nan ong-Yellow lain矢un hina S hina拉ar hand欧hina est Y gtang outh C an olia-C hina P s 4bplate Su Altai Alxa Bayan H Qaidam South C uan-Dian Ch Southw Lhasa Eastern S Qian Qilian The S Tiansh Mong Tarim nggar Ju Korea-China North C Ordo Yanshan

通过比较由CPM-CGCS2000模型得到的我国部分CORS坐标与同一测站在CGCS2000中的已知坐标，验证了本文所建立的CPM-CGCS2000模型的精度。由CPM- CGCS2000模型归算后的坐标是通过以下步骤得到的：①为了获得一个测站在CGCS2000框架的参考历元中的坐标，在ITRF2005的观测历元中，加入由新的CPM模型计算得到的该历元到CGCS2000参考历元的时间间隔的坐标改正量，从而获得该测站在CGCS2000参考历元中的坐标；②将ITRF2005中由步骤①得到的结果用常用的七参数变换方法转换成CGCS2000框架。这两个步骤分别用式（6）和式（7）表示。假设测站i在ITRF2005中的ts历元的坐标为，且该测站在CGCS2000的参考历元，即tc0中的位置为（仍在ITRF2005中），则可通过以下方法获得：

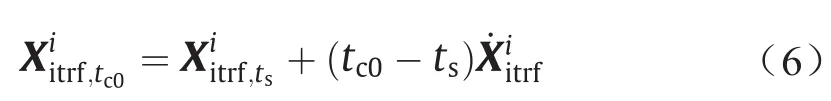
式中，tk表示ITRF2005的参考历元；Tk、Dk及Rk分别表示从ITRF2005到CGCS2000的平移矢量、比例因子和旋转矩阵的变换参数；Ṫk、Ḋk、Ṙk为参数的速率；Xitc0为转换到CGCS2000中的坐标。

本研究中，CPM-CGCS2000的精度通过选定的28个有已知CGCS2000坐标的CORS，由式（7）归算后的坐标与这些站点的已知的CGCS2000坐标之间的差异来评估和验证。图4显示了28个测站在水平方向（其中B和L分别表示经度和纬度）上的位置精度，因为CPMCGCS2000只包含这两个方向的速度分量。

由图4可以看出，大多数基准站的坐标归算精度为-2 ～2 cm，这与CGCS2000框架的± 3 cm精度相比是合理的。精度最差的基准站为LHAS、XIAG、QION、KMIN和XIAA，这是由于这些基准站位于发生地震或海啸的板块上。在CPM-CGCS2000构建中，没有考虑这些事件引起的这些基准站的位置的突然移动或变化，也就是说，这些基准站在事件期间的位移没有得到补偿，并且在式（6）中也没有得到反映。事实上，只有对这些基准站的运动进行阶跃式修正，才能获得这些基准站的精确位置。而本研究所采用的分段处理会因事件的发生而在时间序列中留下“缺口”。因此，这4个基准站的精度较差，不能代表CPM-CGCS2000的实际精度。此外，LHAS位于印度板块和孟加拉国板块挤压的亚板块上。可以认为它位于局部变形区。因此，该测站的实际速度与模拟刚性板块的拟合速度之间存在显著差异。其余测站的精度均优于± 3 cm。基于这些结果，我们可以得出结论，新构建的CPM-CGCS2000可以达到厘米级的精度。

图4. 28个CORS（LHAS：拉萨；WHSH：乌什；TASH：塔什；JIXN：蓟县；CHUN：长春；SUIY：绥阳；HRBY：哈尔滨；HLAR：海拉尔；XIAA：西安；XANY：咸阳；YANC：盐池；TAIN：泰安；BJSH：十三陵；BJFS：房山；SHAO：上海；URUM：乌鲁木齐；XNIN：西宁；DLHA：德令哈；KMIN：昆明；KUMN：昆明；XIAG：下关；XIAM：厦门；WUHN：武汉；GUAN：广州；HAIK：海口；LUZH：泸州；YONG：永兴；QION：琼中）的平面坐标的精度。

4. 非线性运动建模

如果数据中包含偏移量、长期趋势项和时变振幅的周期分量，则必须建立一个非线性模型来描述GPS测站的实际地球物理运动。以往的研究主要集中在提高线速度估计的精度上，而不是使用非线性模型来描述GPS测站的实际运动。尽管国际上最新的ITRF2014 [39]是通过增加测站非线性运动模型而构建的，即通过包含不变趋势和恒定振幅的周期分量来拟合站点时间序列，但仍然不能准确地反映GPS测站的实际移动。本文介绍了基于SSA方法进行非线性运动建模，并与ITRF2014中实现的方法进行了比较。

SSA为数据驱动技术，无需事先了解时间序列中物理现象，只使用时域数据就可从有噪声的时间序列中提取信息[40-44]。近年来，SSA也被用于大地测量研究，它的最新应用之一是对GPS时间序列[9]的季节信号进行建模。在拟合非线性运动方面，SSA相对于正弦函数的优势将在本文的后续部分进行讨论。

图5至图7给出了分别采用正弦函数和SSA对坐标时间序列进行拟合的结果。图5中红色曲线表示高程（U）方向的原始坐标时间序列，蓝线是具有线性趋势和正弦函数的拟合曲线。从拟合残差可以看出，残差中仍含有一些振荡信号。图6则为SSA拟合的结果，可以看出SSA准确地捕捉了坐标时间序列中的季节变化，因此，残差不包含明显的未建模振荡信号。

图5. 具有正弦函数的原始坐标时间序列（红色）和拟合曲线（蓝色）（a）及其在高程（U）方向上的残差（绿线）（b）。

图6.（a）原始时间序列及其趋势；（b）使用SSA方法去趋势时间序列及其拟合曲线（红线）；（c）残差。

图7. TSKB（日本）站的运动轨迹，ITRF2014 [39]（a）的拟合结果[蓝色：原始数据；绿色：由ITRF2014坐标给出的分段线性轨迹；红色：加了地震后参数化变形（PSD）模型]和SSA方法（蓝色：原始数据；红色：SSA建模结果）（b）。

图7显示了使用SSA拟合Tsukuba（日本）测站的特殊实例。在序列中（蓝色的为原始数据），2012年有大约60 cm的大偏移。图7（a）为ITRF2014的拟合的结果，可以看出，虽然ITRF2014提高了框架的精度，但它并不能解决非线性运动建模的所有问题。图7（b）是我们使用SSA进行拟合的结果。这是在序列中移去偏移量，进行时间序列拟合，然后再将偏移量加回之后得到的结果。虽然地震使U方向发生了较大的跳跃，但SSA方法仍与原始时间序列吻合良好，显示了其较强的自适应拟合能力。

SSA过程主要包括分解和重构两个步骤。更多详情见参考文献[45]中的Appendix A。此外，参考文献[45]中的Appendix B1详述了一种我们称为使用伪数据的SSA增强方法（SSA-PD），以解决SSA的相位漂移问题，而另一种用于预测任何特定时间点的GPS站点坐标的SSA预测方法（SSA-P）详见参考文献[45]中的Appendix B2。

4.1. SSA用于内插和误差探测

SSA适用于均匀采样的时间序列。然而，在实际应用中，在GPS测站的原始坐标时间序列中往往存在数据缺失和粗差。因此，在进行非线性运动建模之前，需要对缺失数据进行内插和粗差数据检测。

本研究采用SSA缺失数据（SSAM）内插方法，并结合四分位间距（IQR）准则，采用SSAM-IQR新方法进行粗差检测[43]。由于篇幅的限制，本文不讨论这两种方法，具体可参看文献[9,44]。使用SSAM和SSAMIQR结合的方法的主要优点是不需要事先知道时间序列特性。SSAM模型用于获得补齐缺失数据的值，有关SSAM的详细说明，请参阅参考文献[9,46]。利用2000—2009年我国31个GPS测站的周时间序列对SSAM的性能进行评估。为了便于以后的分析，测站按照中国大陆板块的划分进行分组，如表5所示。内插和粗差检测结果见表6，效果如图8所示。以下所有图中水平轴的单位都是时间年。

表5 每个板块上的测站

从图8可以看出，SSAM-IQR能够正确地检测出所有粗差。利用SSAM模型拟合所有中国GPS测站的时间序列的残差统计结果见表6，从表中可知，大部分插值精度在水平和垂直方向上分别优于5 mm和1 cm。即使永兴站丢失数据超过200 d，最大缺失率达30%，也得到了正确的插值。这里我们只显示了缺失数据超过5%的站点的插值效果。

表6 缺失率、粗差率以及残差的均值和标准差的统计信息

4.2. SSA用于非线性运动建模

缺失数据插值和粗差检测后，所有位置时间序列均采用SSA-PD建模，建模结果如图9所示。由于我们主要关注的是SSA的非线性运动建模的可扩展性，因此我们不考虑只有一个测站的亚板块，如准噶尔和燕山亚板块。

如图9所示，大多数测站的原始信号和建模信号一致性较好，它们的差异实际上反映了模型的精度。模型在E、N和U方向上的精度分别优于± 3 mm、± 2 mm和± 5 mm。尤其在拉萨站的U方向上明显有6 cm的大跳跃，模型精度可达± 5.8 mm，再次显示出SSA具有强大的自适应能力。

图9还显示出位于同一板块上不同测站的坐标时序存在类似的趋势和振荡项，尤其是在水平方向上。因此，我们可以利用具有长时间序列的测站进行非线性运动建模，然后将非线性运动模型扩展到观测周期较短的测站，并将其位置从当前历元转换到任何需要的历元。

图8. 南海板块（a）、中韩板块（b）、华南板块（c）、拉萨板块（d）、鲁东-黄海板块（e）和塔里木板块（f）国家站在东（E）、北（N）和高程（U）方向上的时间序列插值和粗差检测结果。

图9. 在华北平原板块（a）、柴达木板块（b）、华南板板（c）、中蒙板块（d）、川滇板块（e）、拉萨板块（f）、鲁东-黄海板块（g）、塔里木板块（h）、鄂尔多斯板块（i）、南海板块（j）、中韩板块（k）上，我国国家站采用SSA-PD对测站的非线性运动在E、N和U方向上的建模结果。

图9. （续）

图9. （续）

为了研究同一板块内各测站之间的地球物理特性的一致性，以有5个测站的华南板块为例，其中两测站之间的距离如表7所示。由于地球物理因素的影响，垂直方向的运动远比水平运动复杂，高程精度的提高更为重要，因此我们的研究主要集中在U分量上。

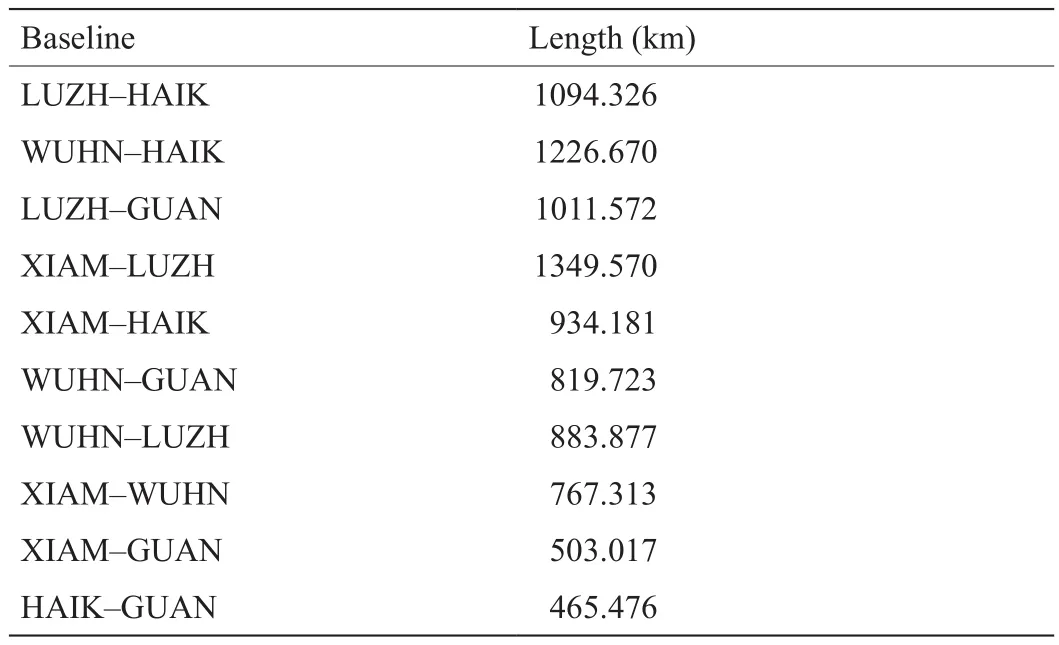
表7 中国华南板块的两个测站之间的距离

首先，利用SSA对华南板块所有测站的U方向上的时间序列去趋势振荡分量进行建模，并在图10中以不同的颜色显示。其次，选取符合要求的时间序列段。从图10可以看出，除了武汉站在2001.882历元附近和广州站在2007.921历元附近有一个大峰值外，其余测站的时序的振幅和相位基本一致。从图9（c）可以看到，2002年武汉站在U方向发生了一次大的跃迁，与广州站2007.921年前后的峰值相比，其在U方向发生了1 cm的突变。因此，本文采用2002.875～2007.384的时间序列作为试验数据，然后用一个测站的非线性位移值代替另一个测站的非线性位移值，并对替换后的数据进行精度评估。图11显示了同一板块中不同长度基线的实验结果。

图10. 华南板块的站点在U方向上的振荡分量。

图11. 在不同距离的几对测站上，即厦门-广州和汉口-广州（a）、武汉-海口和厦门-卢州（b）、卢州-广州和卢州-海口（c）、武汉-广州和武汉-卢州（d）的振荡分量在U方向上的匹配度。

距离500 km以下的两个测站的时间序列具有大致相同的幅值和相位。当两测站之间的距离较大时，两测站的振幅和相位漂移均不同步。因此500 km范围内两个测站的非线性运动有可能用这种方法代替。

4.3. SSA用于GPS测站坐标预测

本研究提出另一种扩展的方法，称为SS A-P来预测任何特定时间的GPS测站的坐标。使用32个国家的GPS测站的10年GPS周坐标时间序列对其性能进行评估。利用前468周样本对信号进行重构，然后利用重构模型对接下来的52个周样本进行预测，以验证模型的预测结果。

显然，如果测站运动比较稳定，那么非线性运动模型的残差就越低，且非线性运动预测的精度也就越高。这种特征在水平方向上可以明显看到。而在垂直方向上，由于同震和震后变形、全球地球物理流体动力学等原因，其运动变得更加复杂。研究发现，基于前几年的建模特性往往无法向前扩展到下一年或精度较差，造成垂直分量的建模精度较低，通常低于水平分量。即便如此，垂直分量的建模精度仍优于± 5 mm。

图12所示的结果表明，预测信号与实际信号之间的差异不大；预测结果的精度相当稳定，在N、E方向上，大多数测站的精度约为± 3 mm（表6）。

SSA-P预测GPS测站在水平方向和垂直方向上的坐标的精度，即使噪声水平大于振荡分量，也有可能获得高精度。对于大多数GPS测站来说，即使在时间序列中存在年和半年的振幅信号，其精度也分别优于± 5 mm和± 1 cm。但是，拉萨和川滇板块的测站预测结果相比其他板块的测站预测结果，其预测结果与板块拟合误差的精度相当。

5. 结论

为实现我国动态大地坐标系的优化，本文提出了几种新的策略或方法，并将其应用于国家GNSS基准站的数据处理和CGCS2000坐标系的维护。具体使用了1720个测站的10年以上的观测数据进行了测试和验证，得出的结论如下：

（1）作为ITRF基准站选取规则的补充，将监督聚类方法应用于CGCS2000框架构建时控制站的选择，估计了1072个国家基准站的速度，且精度显著提高，与未应用该规则估计的速度相比，x、y和z方向上的中误差由0.92 mm∙a-1、0.72 mm∙a-1和0.97 mm∙a-1[3]减小到0.19 mm∙a-1、0.45 mm∙a-1和0.32 mm∙a-1（分别由N、E、U方向上的0.124 mm∙a-1、0.127 mm∙a-1、0.563 mm∙a-1精度转化）。

（2）针对现有软件存在的大规模GNSS数据处理测站数受限的问题，提出了一种新的分区方法，即PSM。PSM产生的基线相对精度大大优于通常使用的GPM，其在水平方向和垂直方向上的位置精度分别为1 mm和2 mm。此外，由PSM得到的坐标比GPM得到的坐标精度更加均匀和稳定。

（3）对于CGCS2000的维护，通过最小二乘估计得到了最适合的国内板块运动模型CPM-CGCS2000，在E、N和U方向上的平均精度分别为± 0.127 mm∙a-1、± 0.124 mm∙a-1和± 0.563 mm∙a-1。板块拟合的最好、最差 和 平 均 值 分 别 为± 0.31 mm∙a-1、± 5.02 mm∙a-1和± 1.62 mm∙a-1。

（4）对于毫米级精度的CGCS2000维护，提出了采用数据驱动和自适应SSA方法。扩展了几种基于SSA的应用，包括用于插值的SSAM方法、用于粗差检测的SSAM-IQR方法、用于GPS测站非线性运动建模的SSAPD方法和用于GPS测站非线性运动坐标预测的SSA-P方法。SSA-PD和SSA-P对水平和垂直方向的位置非线性运动的建模和预测精度都很高，SSA-PD在E、N和U方向上的精度分别优于± 3 mm、± 2 mm和± 5 mm，SSA-P的水平和垂直方向上的1.5年的预测精度分别优于5 mm和1 cm。

值得一提的是，在ITRF2014框架构建时，虽考虑了非线性运动，但基于线性速度的框架维护仍然为厘米级的精度，因此不能满足某些框架维护所要求的毫米级精度，如全球大地测量系统（GGOS）。增强型SSA是分析和提取时间序列趋势、周期分量和噪声的有力工具，极大地提高了CGCS2000框架坐标估计和预测的精度。不足的是，基于SSA-P预测无法直接给出坐标，但利用坐标时间序列和SSA方法可以很容易地得到基准站在任何历元下的坐标，并且由于考虑了测站运动的非连续性和周期性变化，因此SSA方法的精度要高得多。

图12. SSA-P预测华北平原板块（a）、柴达木板块（b）、华南板块（c）、中蒙板块（d）、燕山板块（e）、川滇板块（f）、拉萨板块（g）、鲁东-黄海板块（h）、南海板块（i）、准噶尔板块（j）、塔里木板块（k）、鄂尔多斯板块（l）站在E、N和U方向上的非线性运动结果（蓝色：原始数据；绿色：预测结果）。

图12. （续）

图12. （续）

致谢

本研究由国家重点研发计划（2016YFB0501405）和自然资源创新平台建设与能力提升（A19090）、中国测绘科学研究院基本科研经费（AR1903和AR2005）资助。

Compliance with ethics guidelines

Pengfei Cheng, Yingyan Cheng, Xiaoming Wang, Suqin Wu, and Yantian Xu declare that they have no conflict of interest or fi nancial con fl icts to disclose.