基于圆形模式平面标靶的高精度相机标定方法

辛 睿,武栓虎,李爱娟

(烟台大学计算机与控制工程学院,山东 烟台 264005)

相机标定是三维视觉测量应用过程中的一个重要环节,应用领域非常广泛,从自动精密装配机器人、机器人定位导航到三维目标重建,都需要用到精确的相机标定．最经典的相机标定技术由TSAI[1]在1987年提出,通过使用黑色方块立体压印图形板并采用二步法进行标定可以做到快速估计相机参数,但高精度的三维标靶制作精度成本较高．HIKKLIA[2]基于2块带有圆形模式的垂直平面标靶开创了用椭圆中心点作为特征点标定的先河．将2块垂直的标靶构造三维标靶精度要求较高,不利于大范围的推广．

平面标靶是普遍采用的标定工具,优点是制作简单,精度高成本低．目前流行的平面标靶有2种:基于圆模式的和棋盘模式的．棋盘标靶标定法是ZHANG[3]于2000年提出的,将棋盘角点作为特征对应点,是近年来一直采用的标定方法．但是棋盘标靶在特征点提取时受光照和噪声影响较大,不利于工业应用．因此作为替代,基于圆模式的平面标靶也得到了普遍采用．这是由于圆的成像为椭圆,将椭圆中心作为圆心的特征对应点受环境影响较小,恢复精度高,因此得到了广泛应用．但是将椭圆中心作为特征对应点,由于透视偏差和镜头畸变,并非真实的标靶圆心投影,存在一定的偏差．圆的直径越大,透视偏差和镜头畸变越大,特征点的偏差就越大,从而降低了标定精度．针对这个问题,文献[4-5]提出了基于圆环模式的标定方法．其基本思想是外围采用多个大直径的圆环,在圆环中心使用尺寸小的圆点,以利于克服尺寸大特征点提取精度低的缺点．但文献[4-5]采用圆环模式投影重建和模式匹配的策略对成像圆环中小圆点定位的方法,速度较慢．另外圆环标靶也不利于推广．

针对平面圆模式标靶的最新研究进展是2014年的文献[6],此后未见类似的研究报告,文献[6]全面地分析了2000年发表的文献[2]中方法的不足,并基于圆形模式平面标靶提出了一种标定算法．但作者也指出其唯一不足就是采用文献[7]提供的工具(Calibration Harp):先对镜头畸变先行标定,然后将原始图像映射到非畸变图像空间,检测椭圆中心,通过矫正透视偏差提高标定精度．Calibration Harp畸变标定工具比较昂贵,成本较高,同样不利于推广应用．值得一提的是文献[8]提出了一种相机标定中圆心投影点精确定位方法,但该方法并未考虑镜头畸变产生的影响,因此误差较大;类似地,文献[9]基于三维球形标靶,提出了一种球心投影偏差的校正方法,同样也未涉及镜头畸变带来的偏差．另外,文献[10]提出了一种基于相位标靶的相机标定方法,但相位标靶并不适合在复杂光照环境下的应用,比如机器人导航等．除此之外,大多数研究集中标定算法的研究上,譬如文献[11-12],但在实际应用上,这些方法仍有不足,传统模型和方法依然占据主流．

综上所述,不依赖任何辅助工具,圆模式平面标靶圆心在相机空间的准确定位依然是一未很好解决的问题,本文针对文献[6]的不足,仅仅基于一块圆模式平面标靶,提出了一种同时估计和矫正镜头畸变和透视偏差从而获得圆心在图像空间的精确定位方法．值得一提的是,偏差矫正过程采用迭代策略并和相机参数估计过程独立,从而降低了参数估计过程中误差累计的影响[6],并可通过初始检测的椭圆中心和偏差矫正,获得真实的圆心成像点,从而提高标定精度．模拟数据实验结果表明,通过3次左右迭代就可收敛,矫正后估计的特征点与真实特征点偏差精度可达10-5像素,从而标定结果几乎完全恢复基准参数,证明了该方法的正确性．真实图像标定结果,也达到了理想的结果．

1 相机模型和基于偏差矫正的标定方法

在这一部分,首先给出相机模型和标定方法,然后给出特征点的透视和偏差矫正估计方法,最后给出完整的基于圆模式标靶的高精度标定步骤．值得说明的是,本文方法也可适用于其他更复杂的相机模型．

1.1 相机标定模型

标定过程中,平面标靶上的特征点坐标称为世界坐标,记为[xw,yw,0]T,相机坐标系记为[xc,yc,zc]T,标靶的姿态,包括旋转和平移,记为R,t;图像空间像素坐标为[u,v]T．相机成像过程可描述为:

其中,s为常数比例系数,K称为相机内部参数矩阵,H称为单应矩阵,[u0,v0]T是图像主点,fx和fy为焦距,R、t为标靶的旋转和平移．r1、r2为R的前两列．

(2)

其中:hi为单应矩阵Η的第i个行向量．

根据上式,由多幅(≥3)不同姿态的标靶图像可以估算相机内部参数矩阵K以及各标靶的姿态[Ri,ti]的初始估计[3]．

在相机成像的过程中,相机镜头会产生畸变．令[u,v]T为像点的非畸变位置,令[u′,v′]T为畸变位置,那么有下列关系:

(3)

其中:k1、k2、k3为径向畸变系数,p1、p2为切向畸变系数,r是该点距成像中心的距离．

假设从N个不同姿态得到了N幅标靶图像,每幅图像上有M个像点．利用前述单应矩阵H和各标靶姿态的初始估计,并设置初始畸变参数0,再通过最小化以下函数求解畸变参数的初始估计:

(4)

其中:Mj表示第j个像点对应的标定板上的三维点,P(K,Ri,ti,Mj)为Mj所对应的第i幅图像的投影,mij=[uij,vij]T为式(3)中矫正得到的非畸变像素位置．最小化问题最终可以通过Levenberg-Marquardt算法[13]优化求解．通过上式可估算出初始畸变参数,利用初始畸变参数和式(3)对成像特征点做矫正,再重新估计相机内部参数矩阵K和各标靶的姿态,然后利用公式(4)对畸变系数重新估计．上述过程一直进行到预设的精度达到为止．

1.2 基于偏差矫正的相机标定策略

由于透视偏差和图像畸变的存在,当标定平面与图像平面存在旋转和位移时,标定板上的圆形投影在图像平面之后会变成近似的椭圆,但成像椭圆的中心并非标靶上对应圆心的投影,因此利用成像椭圆中心进行相机标定会降低标定精度．针对这个问题,本文提出了采用迭代的方法对投影椭圆中心进行偏差矫正．

偏差矫正基于如下事实:利用成像椭圆中心进行标定时,由于存在透视和畸变偏差,得到的相机内部和外部参数并不精确,因此利用得到的相机内部和外部参数重建图像也会产生偏差．如图1所示,实线椭圆为成像椭圆,虚线椭圆为重建椭圆,两者并不重合,也会存在位置偏差．也就是说成像椭圆中心和重建椭圆中心并不重合．另外,实线椭圆的中心(图1十字线)就是重建虚线椭圆的对应标靶圆心的投影(标定时使用)．换句话说,虚线椭圆的中心是图1中实心点,其真实的标靶圆心投影就是图1中十字线(对应实线椭圆的中心)．因此如果移动虚线椭圆和实线椭圆重合,那么图1中十字线(成像椭圆中心)移动到位置就是成像椭圆对应标靶圆心的精确成像点．即在成像椭圆中心坐标上加上使2个椭圆重合的偏差向量,就能得到无偏差的标靶圆心投影估计．

图1 成像椭圆与重建椭圆对比

从上面分析不难看出,圆心在图像投影空间的精确定位,可以通过图像重建来达到,即利用估计的相机内部和外部参数对平面标靶进行投影重建,如果重建图像和实际获得的标靶图像重合,就可获得圆心投影的精确估计．重建图像和实际图像的重合度估计可以采用图像匹配的方法,但这种策略速度慢,不利于实际应用．在这里,本文采用一种简便实用的方法:对实际图像获得的近似椭圆中心和重建图像近似椭圆的中心进行比较,就可以同时获得透视和畸变偏差估计,得到精确的圆心投影估计．椭圆的中心估计有2种方法,圆锥曲线投影法[6]和采样投影拟合法．圆锥曲线投影法的优点是无须对标靶上的圆轮廓采样,可以和相机内部和外部参数结合一次得到圆心投影,但圆锥曲线投影法仅适合在无畸变空间进行．当镜头存在畸变时,将圆锥曲线投影法得到的椭圆中心变换到畸变空间,并不是真正的圆心的成像点,存在一定的畸变偏差,这也正是文献[6]首先利用Calibration Harp辅助工具进行镜头畸变参数标定,然后在畸变校正图像上进行透视偏差矫正的原因．因此,本文采用下述采样法．

估计透视和畸变偏差时,需要对标靶上的圆轮廓进行采样,并投影到图像空间拟合椭圆(图1中虚线椭圆)和原始空间中检测到的椭圆进行比较．平面标靶上每个圆上采样点的世界坐标可按照下式计算:

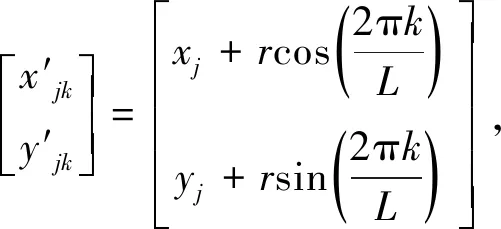
(5)

其中:[xj,yj]T为平面标靶上第j个圆的中心坐标,L为采样点数,k=0,1,2,…,L-1为每个圆上的采样点下标,r为标靶上圆的半径．

设检测的椭圆中心坐标为[u,v]T,作为矫正基准保持不变．利用相机参数投影拟合的椭圆中心记为[u′,v′]T．那么透视和畸变综合偏差[Δu,Δv]T可由下式得到:

(6)

设[u′,v′]T为重新估计的标靶圆心成像坐标,其初值[u′,v′]T=[u,v]T．根据上述计算方法,可由式(7)得到重估的标靶圆心成像坐标:

(7)

利用重新估计的圆心投影[u′,v′]T和1.1节描述的算法,对相机参数重新计算,然后再计算重建偏差,重估标靶圆心成像坐标,再对相机参数重新估计．这个过程一直进行下去,直到偏差不再变化为止．在实际计算过程中,设置dt=‖[Δu,Δv]T‖,t为迭代次数,d0=0,设ε=|dt+1-dt|,当ε小于预置的精度时停止迭代．

综上所述,总体标定步骤具体如下:

步骤1 准备一块上有M个圆的平面标靶,以不同姿态拍摄N幅图像(N≥3),检测的椭圆中心用[uij,vij]T表示,其中i=1,2,…,N,j=1,2,…,M．在后面偏差估计过程中始终保持不变;

(8)

并设ε=|dt+1-dt|,d0=0,其中t为迭代次数;

步骤4 按照公式(5)对标靶圆轮廓进行采样,按照最新估计的相机参数将采样点投影到图像空间,并拟合椭圆,得到的椭圆中心记为[uij′,vij′]T;

步骤5 按照下式计算检测的椭圆中心[uij,vij]T与重建拟合的椭圆中心[uij″,vij″]T的偏差向量[Δuij,Δvij]T和平均偏差dt:

(9)

步骤6 如果平均偏差ε小于预定精度,算法结束,否则进入第7步;

步骤7 重新估计标靶圆心的成像坐标:

(10)

步骤8 利用第7步得到的重估的圆心成像点,返回第3步继续．

通过以上的标定过程可知,本文算法和相机模型参数估计过程是独立的,因此通过简单修改,也适合在相机内部参数已经标定好的情况下,得到高精度的姿态估计参数．姿态参数估计是只需一幅标靶图像,可以固定相机内部参数并通过矫正畸变和透视偏差得到高精度的特征对应点,从而得到高精度的标靶姿态估计．这在实际工业领域有广泛应用,比如汽车四轮定位,机器人定位导航等等．具体修改方法如下:步骤1改为拍摄一副图像即N=1;将步骤3改为估计标靶的姿态参数,即旋转矩阵R和平移向量t(相机参数已经标定好,保持不变)．

2 实验与结果

2.1 模拟标定实验

本模拟实验的目的是要验证,仅仅根据成像椭圆中心,通过本文提出偏差矫正方法就可获得精确的标靶圆心对应特征点,从而恢复精确基准相机参数．在模拟实验中,相机的基准参数由实际标定过程获取的参数稍加修改得到．实验所用的椭圆及其中心坐标可利用基准相机参数和特定尺寸的圆模式标靶生成．

模拟实验图像分辨率为680像素×480像素,标靶圆心距为10 mm,圆半径为3 mm的7×7圆形阵列标靶．相机基准参数包括相机内部参数和13组不同的姿态参数,由此获得13幅不同图像．

首先,使用式(5)对标靶圆轮廓进行采样,采样点数为50(实验发现24以上都可行),并使用基准相机参数将其投影到图像空间,并拟合得到椭圆中心,将其作为对应特征点使用1.1节算法进行标定,得到经典算法[3]标定结果．然后将其作为初值使用本文算法进行标定．算法迭代3次,结果收敛．表1给出了标定结果对比．从表1结果可以看出与基准相机参数比较,经典算法[3]得出的最大误差为0.1像素左右,本文算法的最大误差为10-5像素左右,基准相机参数完全得到恢复．

表1 模拟实验结果对比

另外,为了说明本文算法利用椭圆中心和矫正偏差估计得到的对应特征点精确性,我们利用相机基准参数对标靶圆心的进行投影得到真实的对应特征点．图2给出了真实对应特征点(标靶圆心成像坐标)和椭圆中心坐标的误差分布如图2(a)和本文算法估计得到的恢复标靶圆心成像坐标误差分布图2(b),均方误差分别为0.106 068像素和1.465 16×10-6像素．从图2(a)可以看到真实对应特征点(标靶圆心成像坐标)并非椭圆中心,误差分布较大,因此利用椭圆中心进行标定降低了精度．而通过本文算法利用椭圆中心作为初始值得到的对应特征点几乎恢复了真实的特征点．

由此可见,只要能够精确检测到椭圆中心坐标,按照本文算法可以精确估计真实的标靶圆心成像坐标,得到理想的标定结果．相比较文献[6]中方法,由于首先要利用Calibration Harp畸变标定工具标定畸变参数,工具本身存在检测、量化等误差,对模拟结果有一定影响,其模拟实验精度获得的相机参数最高精度为0.008像素左右,而我们的模拟误差最大为10-5像素．

图2 标靶圆心成像坐标估计误差分布

值得一提的是,本文算法收敛速度很快,无论是模拟图像和实际图像,经过3次左右迭代就能达到收敛目标．原因很简单:椭圆中心作为标靶上圆心的对应有偏差,但仍然是较好的近似,由此计算的相机内部和外部参数同样也是一较好的逼近,这也是圆模式平面标靶多年来广泛应用的原因．实际上,从原理上看,本文的策略是利用初始相机参数重建的椭圆图像和原始椭圆对比,迭代1次偏差几乎可以得到校正,参考图2(c),但校正后,利用重新计算的相机参数重建的椭圆和原始图像中椭圆可能还存在较小的误差,因此,本文采用多次校正的策略,发现4次迭代,相对收敛误差就可达到10-5像素(预设阈值)．

2.2 实际图像标定实验

在对实际图像进行标定时,真实的圆心投影点未知,因此无法通过特征点的恢复来验证精度,但可通过椭圆重建的重合度来验证算法的有效性．即可以利用标定得到的相机参数对标靶进行投影重建得到椭圆图像,并和原始对应椭圆图像比较其重合度．而椭圆的重合度可通过比较其中心偏差来估计．

实际图像实验图像分辨率设为1280像素×1024像素．标靶为5×5圆阵列,圆直径为22 mm,中心距为27 mm,实验总共获取12幅不同姿态的图像．

首先,对实际图像提取椭圆中心作为特征点标定相机,然后再使用本文算法进行迭代,算法3次后收敛,如图3(c)为迭代误差曲线图．

图3给出了椭圆中心重合度误差分布对比散点图．传统标定方法[3]结果重合度的均方误差为0.141 984像素,本文算法的均方误差为0.018 032 5像素．从图3可以看出,由于透视投影和镜头畸变,实际检测的椭圆中心和真实的标靶圆心的成像点并不重合,因此利用椭圆中心标定得到的相机参数重建椭圆和实际图像椭圆中心偏差较大,而采用本文的算法大大消除了透视和镜头畸变产生偏差,估计的特征点更接近真实标靶圆心成像点,因此重建误差也很小．同时说明本文算法可以得到的标定结果精度更高．我们注意到实际图像和模拟实验相比精度相差较大,这是由于实际数字图像的获取存在一定的量化误差和环境噪声,椭圆的识别存在误差,因此无法精确估计椭圆的中心坐标造成的．另外,标定精度也会受图像分辨率的影响;在同样的噪声环境下,拍摄图像的分辨率越高,其标定精度也会相应提高．

值得说明的是,由于镜头畸变和透视偏差,标靶上圆的成像只是近似的椭圆,但并不影响本文算法．只要检测图像的特征点和重建图像的特征点在标定时特征一致,本文算法就可以通过矫正透视投影和镜头畸变产生的偏差,提高标定精度．

图3 传统标定结果和本文算法重建误差分布

3 结束语

特征点精确估计是相机标定过程中非常重要的部分．圆模式平面标靶是一常用的相机标定工具,相对棋盘标靶,有制造容易、特征点恢复受光照和噪声的影响较小的特点．但由于透视和镜头畸变,提取的椭圆中心会和实际标靶圆心成像点产生偏差,从而降低了标定精度．本文提出了一种通过透视偏差和畸变偏差矫正精确估计圆心实际成像坐标的方法和相机参数标定策略,可以和现有的相机标定方法无缝结合,得到高精度的标定结果．另外,在相机标定好的情况下,也可以使用本文算法产生高精度的标靶姿态参数,以应用于机器人引导、定位等领域．值得一提的是,本文的研究成果已应用到基于3D视觉的汽车四轮定位中,并取得了良好的效果．