基于谱间相关性的高光谱图像稀疏分解算法

王 丽，王 威，刘勃妮

〈图像处理与仿真〉

基于谱间相关性的高光谱图像稀疏分解算法

王 丽，王 威，刘勃妮

（西安航空学院 电子工程学院，陕西 西安 710077）

针对高光谱图像邻近波段相关性强的特点，结合粒子群优化算法的快速寻优能力，提出一种基于谱间相关性的高光谱图像稀疏分解算法。将高光谱图像分组为参考波段图像和普通波段图像，参考波段图像采用粒子群寻优找到最优原子，实现稀疏分解。普通波段图像的最优原子由两部分构成，一部分原子从参考波段图像的最优原子继承而来，继承个数由普通波段图像与参考波段图像的谱间相关性确定，其余原子则由粒子群搜索得到。对高光谱数据集进行稀疏分解，验证算法的分解效率，结果表明，在重构图像精度相当的条件下，稀疏分解速度比正交匹配追踪算法快约18倍。

稀疏分解；谱间相关性；粒子群优化；正交匹配追踪；高光谱图像

0 引言

高光谱图像包含丰富的二维空间几何信息和一维光谱信息，适用于目标探测与识别、图像分类等领域[1-5]，信息量的剧增给数据的存储传输带来挑战。压缩感知理论指出，在满足信号稀疏或可压缩的前提条件下，信号的采样能够突破传统奈奎斯特定律的限制，大大降低数据量，因此，应用压缩感知理论处理高光谱图像得到众多研究者的关注[6-8]，首要工作是实现稀疏表示，后续工作是实现稀疏表示下的高光谱图像去噪、分类、解混[9-16]等。常用的稀疏分解算法包括正交匹配追踪（orthogonal matching pursuit，OMP）[17-18]和基于线性规划的基寻踪算法（basis pursuit，BP）[19]，OMP算法由于收敛快且精度高被大量采用。采用冗余字典对高光谱图像信号进行稀疏表示时，算法的复杂度较高，给稀疏分解算法的计算效率提出新的挑战。在考虑进化算法寻优能力较强的思想下，作者利用粒子群优化（particle swarm optimization，PSO）对OMP算法进行改进，提出了基于粒子群优化的稀疏分解算法（particle swarm optimization algorithm based on orthogonal matching pursuit，PSO_OMP）[20]。在保证重构精度的条件下，利用谱间相关性强去进一步提高稀疏分解效率是本文的研究问题。

1 基于谱间相关性的稀疏分解算法

1.1 基本框架

高光谱图像的光谱分辨率高，邻近波段具有极强的相关性，但相邻波段之间的谱间相关性会随着波段间距的增大而减小，只有一定间距内的波段会保持较大的相关性。在稀疏分解过程中，借鉴高光谱图像分组处理的思想[21]，将所有高光谱图像分为参考波段图像和非参考波段图像，采用不同的最优原子搜索方式，提高稀疏分解的计算效率。

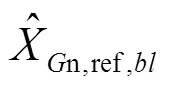
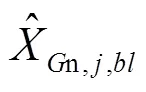
1.2 稀疏分解过程

参考波段图像利用PSO_OMP算法完成稀疏分解，得到最优原子集合表示为：

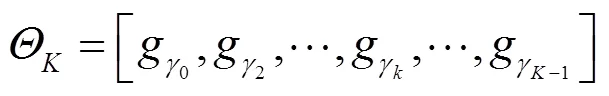
式中：是最优原子的个数。

非参考波段图像与参考波段图像具有极强的相关性，表明两个图像之间具有共性特征，可用相同的原子进行稀疏表示。非参考波段图像的部分最优原子可从参考波段图像的最优原子集合中继承而来，继承个数in表示为：

in＝round(××) (1)

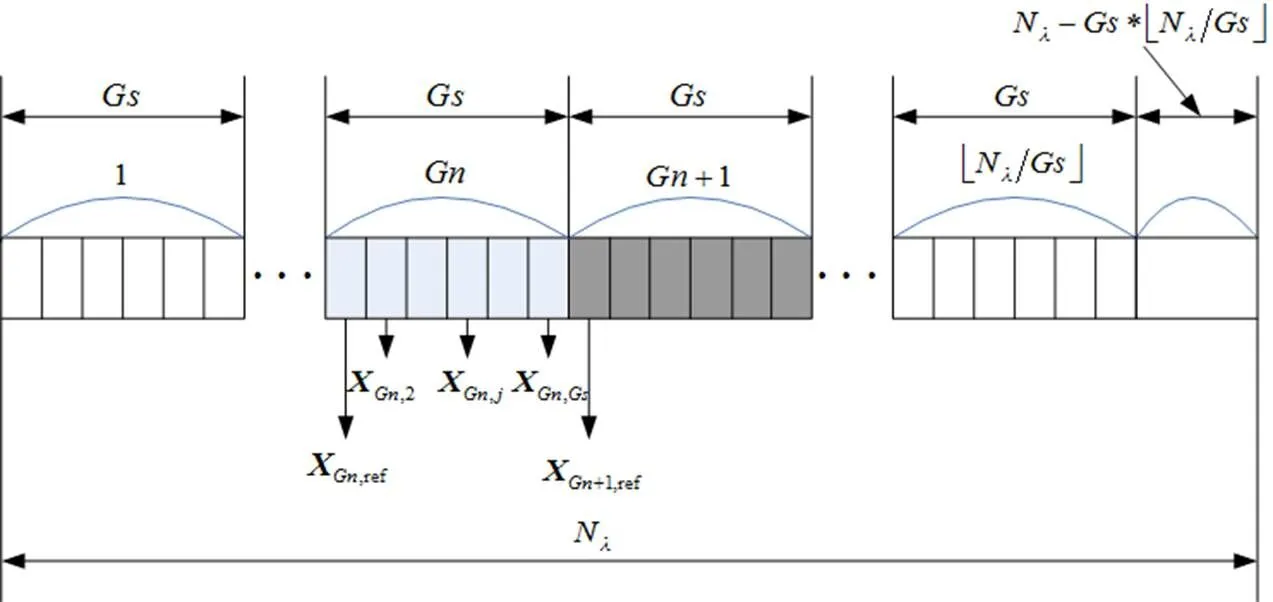
图1 波段分组示意图

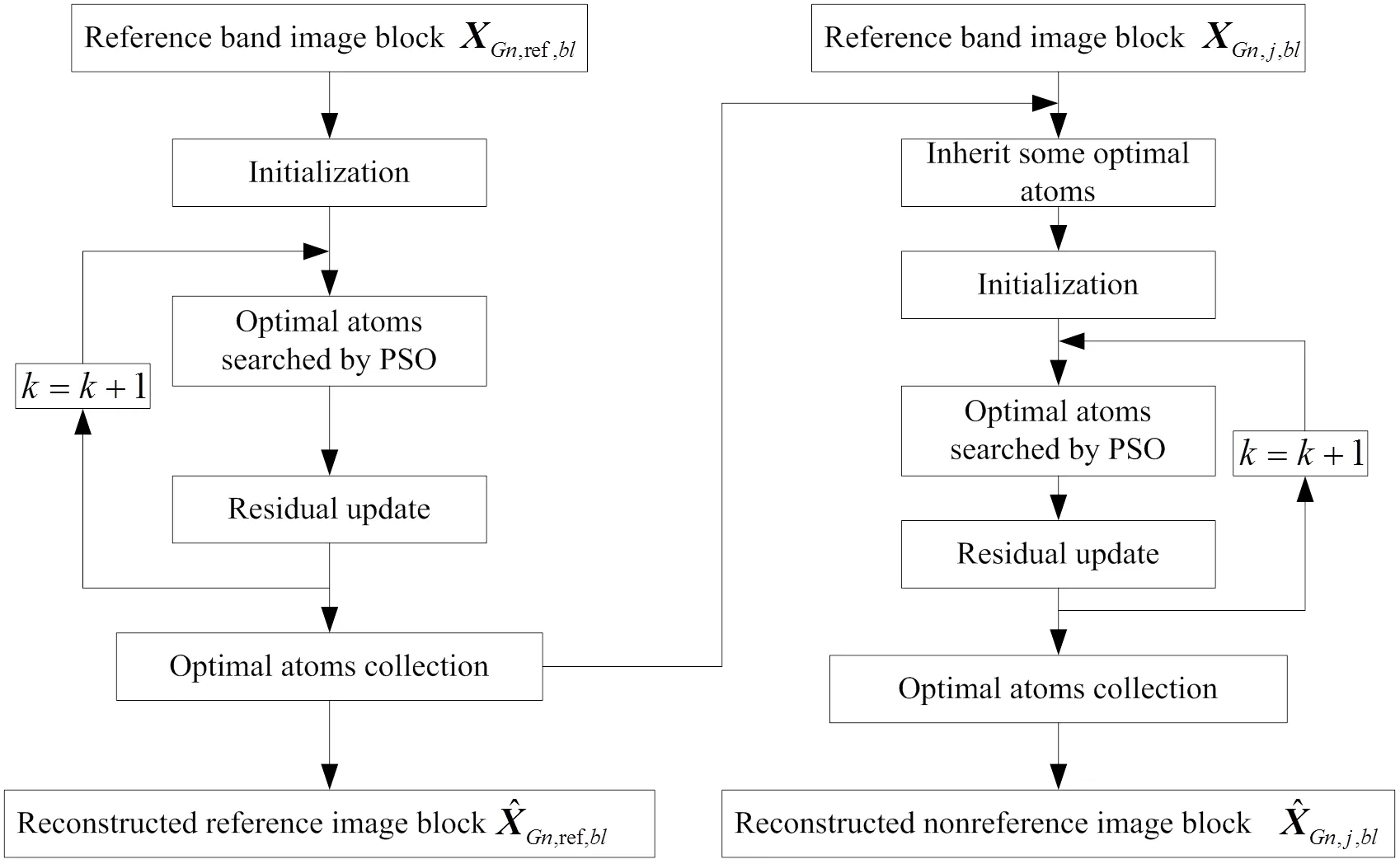
图2 基于谱间相关性的稀疏分解算法框架

式中：round(×)表示取整；是继承系数；是非参考波段图像与参考波段图像的谱间相关性，计算公式为：

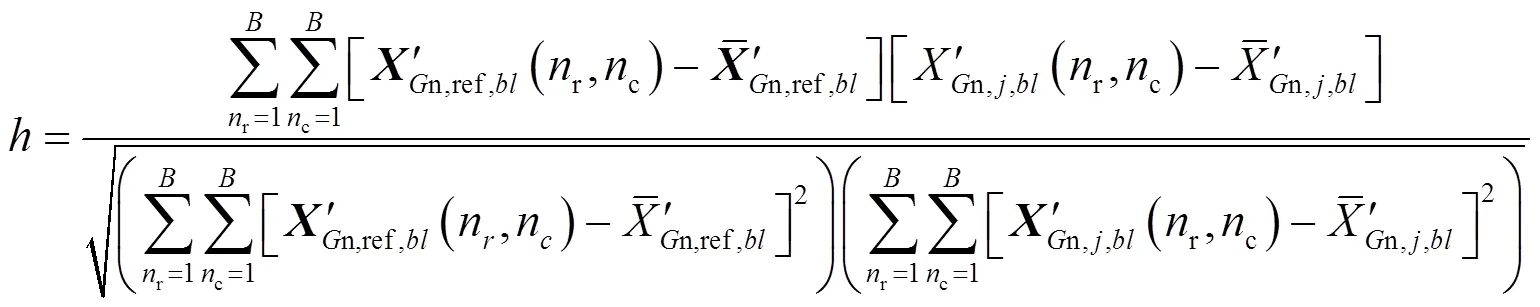
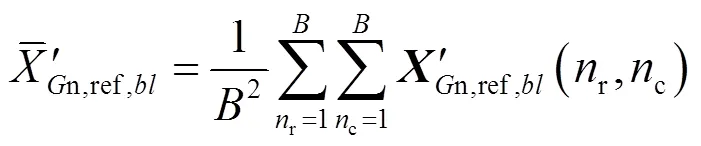
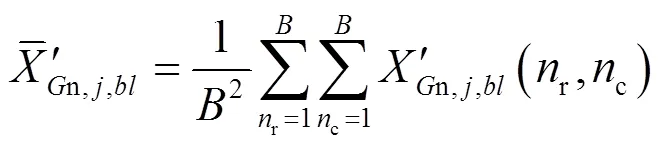
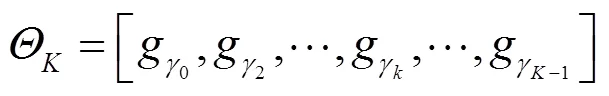
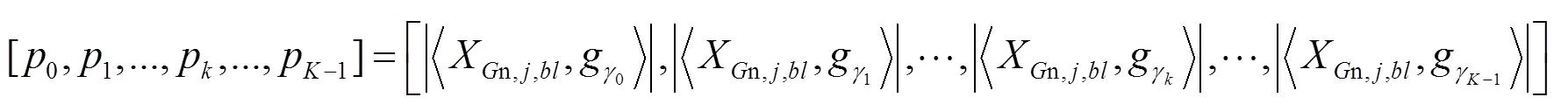
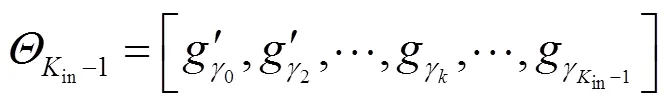
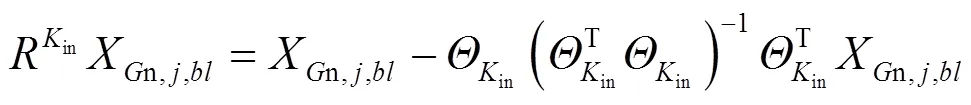
将此残差作为初始值，利用PSO算法搜索－in个原子，得到表示非参考波段图像块的个最优原子。

1.3 算法主要步骤

以单个图像块Xn,j,bl为例说明算法MPSO_OMP的执行过程，其他图像块与之相同，总结如下：

算法：MPSO_OMP

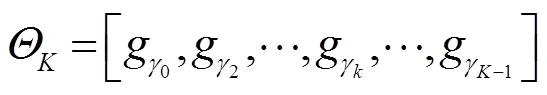
Step 1：根据公式(1)计算Xn,j,bl与Xn,ref,bl的谱间相关性，并计算继承个数in；

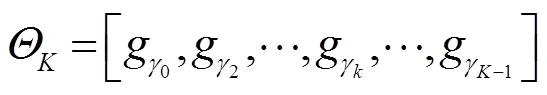
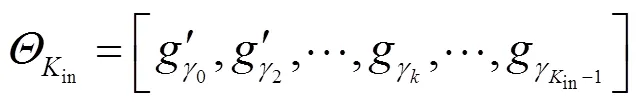
Step 4：利用PSO寻找最优原子，达到最大进化代数max后立即终止搜索，输出best；

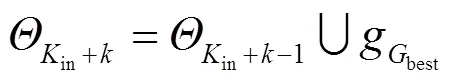
Step 7：判断是否达到最大分解次数－in，若不满足则＝＋1，重复Step 4～Step 6；若满足则停止迭代。

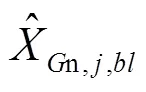
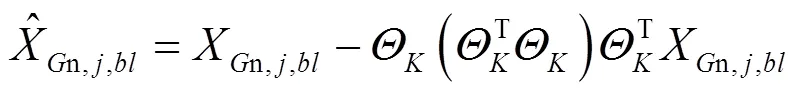
2 实验结果与分析

2.1 高光谱数据集

选择4组高光谱图像评估稀疏分解算法的性能，分别是来自AVIRIS采集的Cuprite 1、Cuprite 2、Indian Pines以及ROSIS采集的Pavia University。原始数据集中的水汽波段和噪声波段均已移除，且根据分块大小＝16对图像进行了空间剪裁，4组数据的基本情况见表1。高光谱数据第50个波段的原始图像如图3所示。

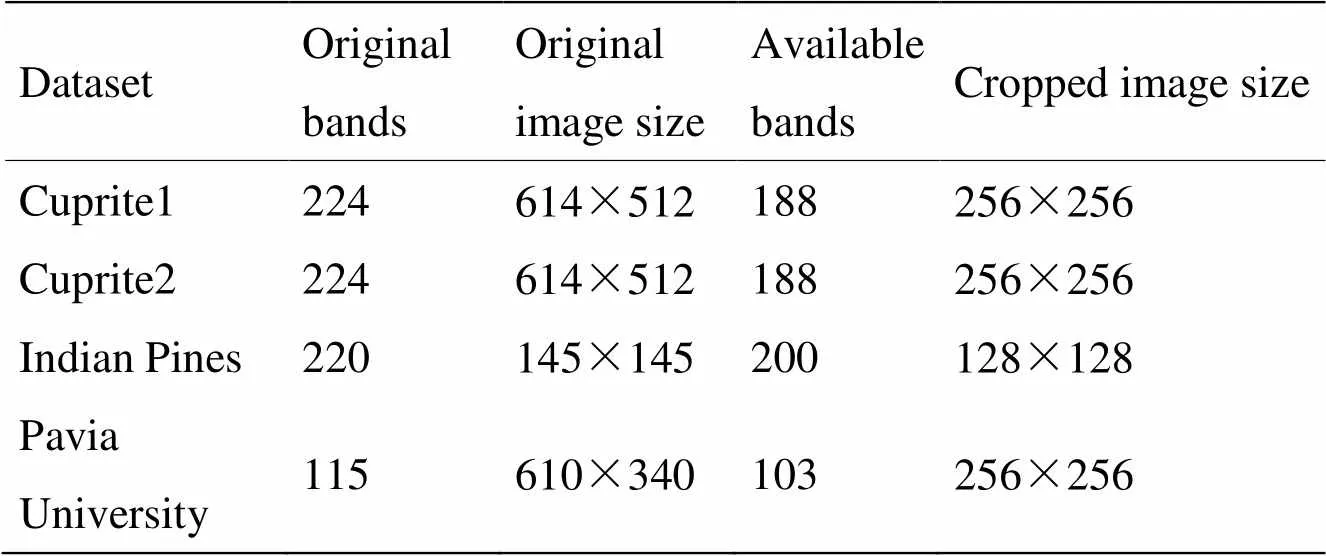
表1 四组高光谱数据集的基本情况

2.2 实验参数设置

不论是利用OMP算法、PSO_OMP算法还是算法MPSO_OMP对高光谱图像进行稀疏分解，均需设定最大分解次数，该参数对算法的时间复杂度及重构图像的精度具有重要影响。所提算法MPSO_OMP还需设定的参数是粒子群优化中的最大进化代数和种群大小，以及继承系数。分组大小s的选择会影响算法性能，通常来说，s越小，组内的谱间相关性越强，非参考波段图像块能够从参考波段图像块继承到更多的最优原子，稀疏分解效率越高，但此时分组个数也较多，时间复杂度也会增加。当高光谱成像仪的光谱分辨率较高时，相对较大的分组也能保证组内图像的强相关性，重构精度也能得到保证。根据实验场景对应的传感器的光谱分辨率，同时考虑到计算复杂度，分组大小选择为s＝8。

图3 四组高光谱数据的第50个波段的原始图像

利用重构图像的峰值信噪比（peak signal-to- noise ratio，PSNR）和运行时间对算法性能进行评价。实验的运行软硬件环境为：AMD四核CPU，3.80GHz，16G内存，Matlab2012b。单个图像块的重构PSNR计算公式为：

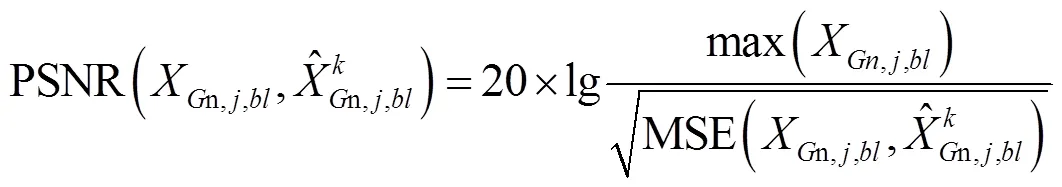
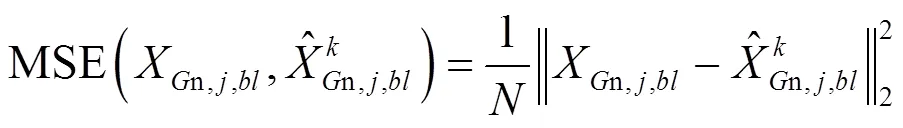
2.2.1 粒子群参数的确定

首先利用算法PSO_OMP对4组高光谱数据的第50个波段图像进行稀疏分解，分析最大进化代数、种群大小和分解次数对算法性能的影响。粒子群优化中最大进化代数max的变化范围是5～50，间隔是5，种群大小op的变化范围是5～50，间隔是5，分解次数的变化范围是10～100，间隔是10。同一参数下算法PSO_OMP运行10次以消除算法的随机性，图4给出的是Cuprite 2重构图像的平均PSNR随参数的变化。分解次数为50次时，平均重构PSNR随最大进化代数和种群大小的变化如图4(a)所示。同一种群个数下，PSNR随着最大进化代数的增加没有大幅度的增加，即最大进化代数对PSNR的影响不大。同一最大进化代数下，随着种群个数的增加，PSNR以较慢的速度逐渐增加。

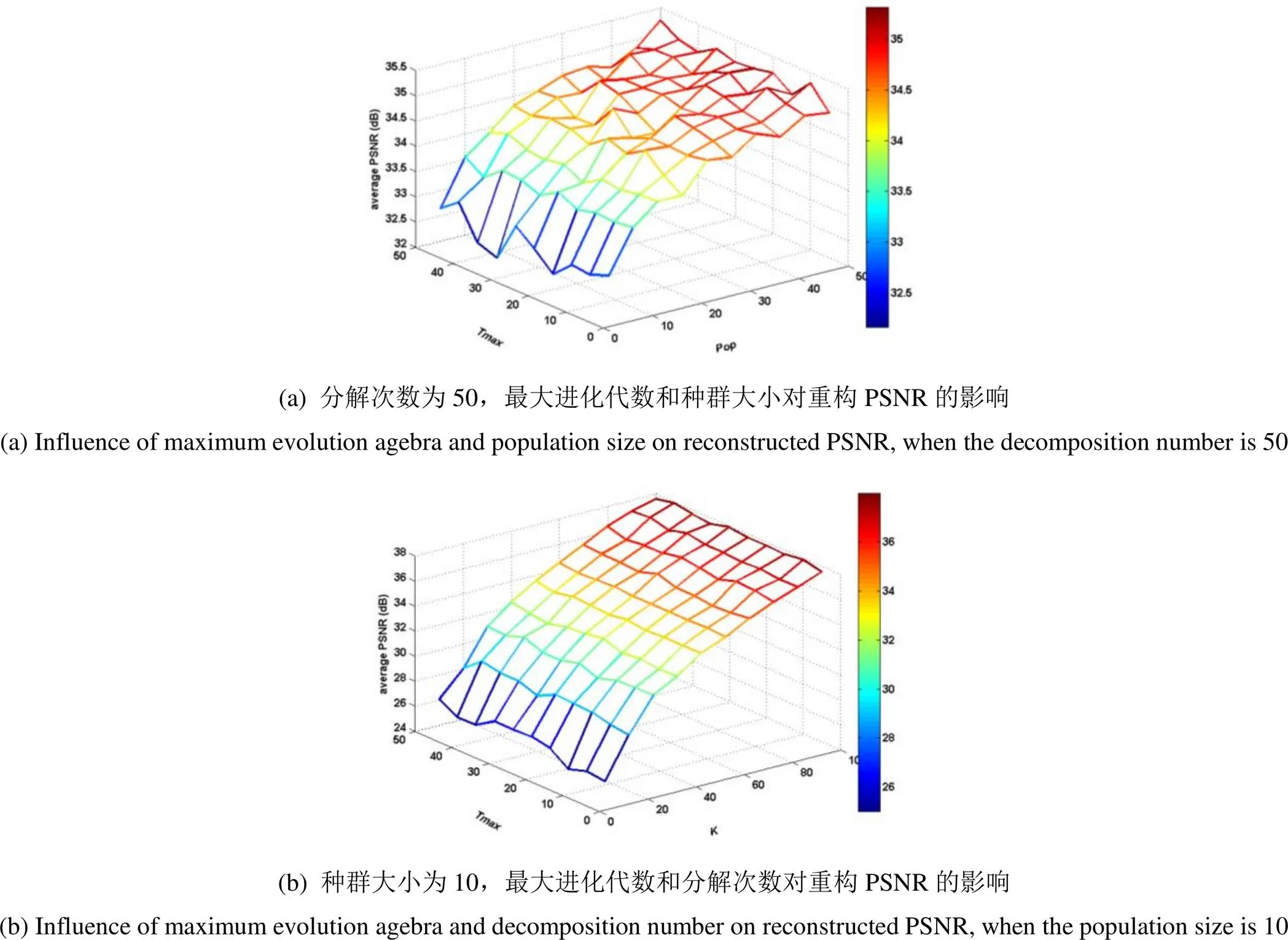
种群大小为10时，最大进化代数和分解次数对重构PSNR的影响如图4(b)所示。同一分解次数下，PSNR随着最大进化代数的增加仅有小幅度的振荡，进一步地表明最大进化代数对重构精度的影响不大。同一最大进化代数下，随着分解次数的增加，PSNR不断增加，且与图4(a)中种群个数增加所引起的PSNR增长相比，分解次数的增加更能令PSNR快速增长。最大进化代数为5时，种群大小和分解次数对重构性能的影响如图4(c)所示。同一分解次数下，PSNR随着种群数量的增加会不断增加，但增长的速度较慢。同一种群数量下，随着分解次数的增加，PSNR会逐渐增加，增长速度快于种群数量增加所引起的PSNR增长，进一步地说明增加分解次数更有助于提高PSNR。

当最大进化代数和种群个数逐渐增大时，粒子群优化过程将需要从更多的粒子中经过多次进化才能找到最优原子，即在二者的影响下，时间复杂度均会不断增加。其他3组高光谱图像的实验结果与Cuprite2相似，综合考虑重构精度和计算复杂度，将粒子群优化的最大进化代数设置为max＝5，种群大小设置为op＝10。

2.2.2 分解次数的确定

利用PSO_OMP算法和OMP算法对4组高光谱数据集的第50个波段图像进行稀疏分解，设定算法在分解次数达到150次时终止。图5给出两种算法得到的重构PSNR随分解次数的变化，其中粗线是OMP分解次数达到50次时，利用50个最优原子对原始图像进行稀疏表示后，得到的重构图像的精度。实验结果表明，算法PSO_OMP仅用50个原子无法达到OMP算法的重构精度，这是因为：OMP算法的每次分解过程中，能够从冗余字典的所有原子中寻找到与残差最匹配的原子，性能得到保证。粒子群算法具有随机性，每次分解寻找到的最优原子可能并不是与残差最匹配的原子，因此需要寻找到更多的原子才能充分表征原始图像的特征，才能达到OMP算法的重构精度。如果将OMP算法利用50个原子得到的重构图像的PSNR作为标准，Cuprite1和Cuprite2大约需要80个原子左右才能达到此标准，而Indian Pines和Pavia University大约需要120个甚至更多的原子才能达到与OMP算法相同的精度。据此，OMP算法的最大分解次数设定为＝50，针对4组高光谱数据集，算法PSO_OMP的最大分解次数分别设定为＝[100, 100, 150, 150]。

2.2.3 继承系数的确定

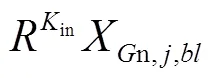
对非参考波段图像进行稀疏分解时，继承系数的选择是影响MPSO_OMP算法性能的主要因素。利用MPSO_OMP算法对4组高光谱数据集的第5个分组内（即波段序号为41～48）的所有波段图像进行稀疏分解，分析继承系数对重构性能的影响。继承系数的变化范围是0～1，间隔为0.1。图6给出不同继承系数下，Cuprite1和Indian Pines两个高光谱数据集的平均重构PSNR及运行时间。

图5 OMP算法和PSO_OMP算法的重构PSNR随分解次数的变化

当谱间相关性确定时，继承系数越小，继承得到的最优原子个数越少，粒子群所需搜索的原子个数越多，此时可用更多的原子去表示图像的差异性，重构性能较好。当继承系数逐渐增大时，从参考波段图像的最优原子集合中继承的原子个数越多，粒子群所需搜索的原子个数越少，重构性能会出现一定程度的下降。在继承系数逐渐增大的过程中，因粒子群算法具有随机性，重构PSNR会出现不同程度的振荡。整体来说，重构PSNR的下降速度较慢，从继承系数为0增加至继承系数为1时，重构PSNR的下降值保持在1dB左右，说明算法仍能保证重构精度。

从计算复杂度来看，MPSO_OMP算法的计算复杂度主要由继承原子的选择过程与其他原子的粒子群搜索过程决定。与继承原子的选择过程相比，粒子群搜索过程更耗时。因此，随着继承系数的增大，继承原子数不断增多，粒子群搜索的原子数不断降低，则算法的计算复杂度会逐渐降低，如图6所示。综合考虑重构性能和重构计算复杂度，当继承系数选择为0.5时，重构PSNR的下降幅度保证在0.4dB以内，而运行速度却能提高1.3倍左右，故将MPSO_OMP算法中的继承系数确定为＝0.5。

2.3 实验结果分析

利用OMP算法、PSO_OMP算法和MPSO_OMP算法对4组高光谱图像进行稀疏分解，分析算法的性能。OMP算法是指对所有波段图像采用OMP进行稀疏分解，最大分解次数＝50。PSO_OMP算法是指对所有波段图像采用PSO_OMP算法进行稀疏分解，最大分解次数＝[100, 100, 150, 150]，最大进化代数max＝5，种群大小op＝10。MPSO_OMP算法是指对高光谱图像进行分组后，参考波段图像采用PSO_OMP算法进行稀疏分解，非参考波段图像采用MPSO_OMP算法进行稀疏分解，最大分解次数＝[100, 100, 150, 150]，继承系数＝0.5，粒子群中的最大进化代数max＝5，种群大小op＝10。表2给出3种算法的实验结果，表中的平均PSNR是高光谱数据集所有波段图像重构PSNR的均值，运行时间是完成单个波段稀疏分解所需的平均时间，加速比是指以OMP算法的稀疏分解速度为标准，算法PSO_OMP和算法MPSO_OMP的加速倍数。

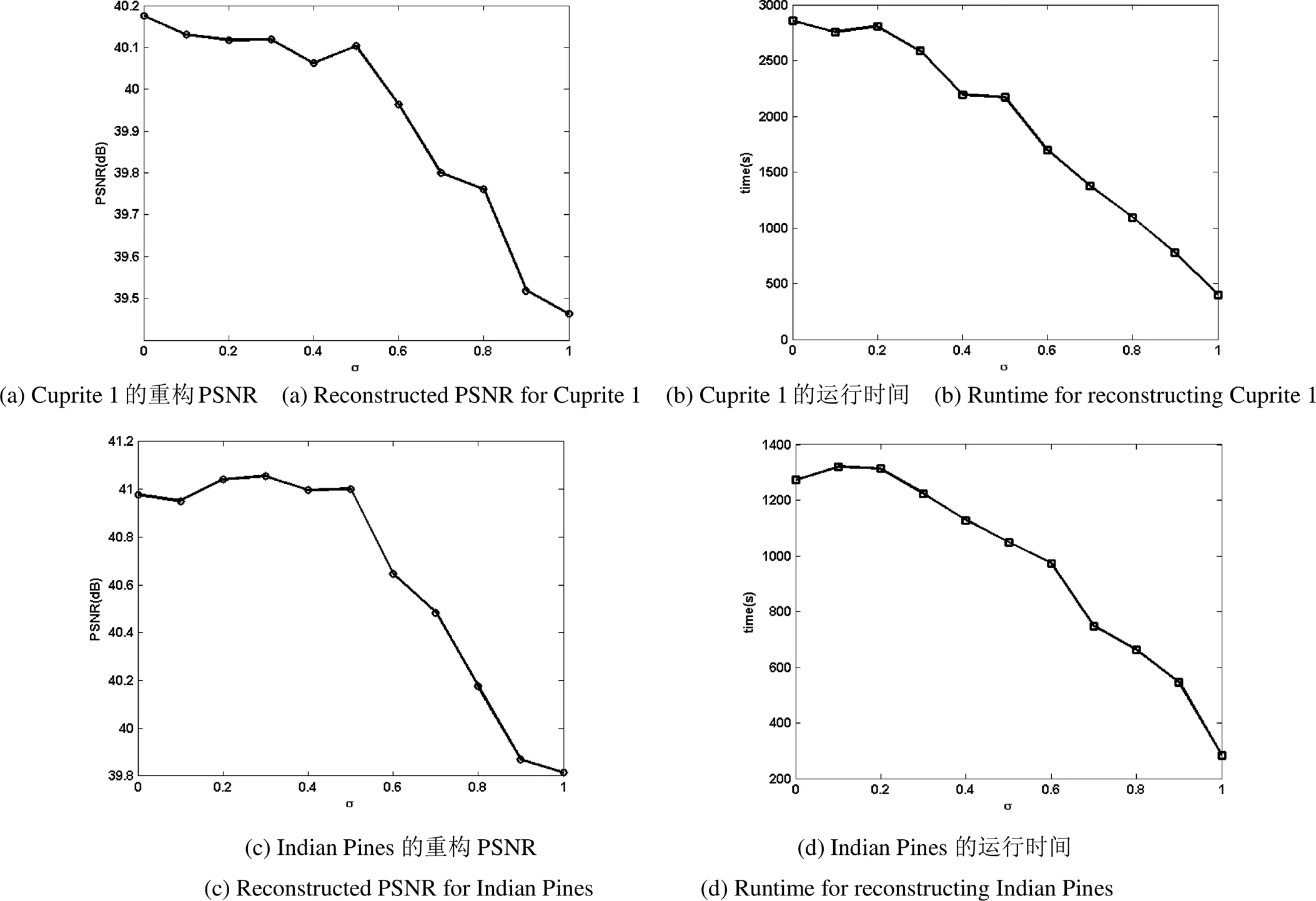
图6 继承系数对算法MPSO_OMP的影响

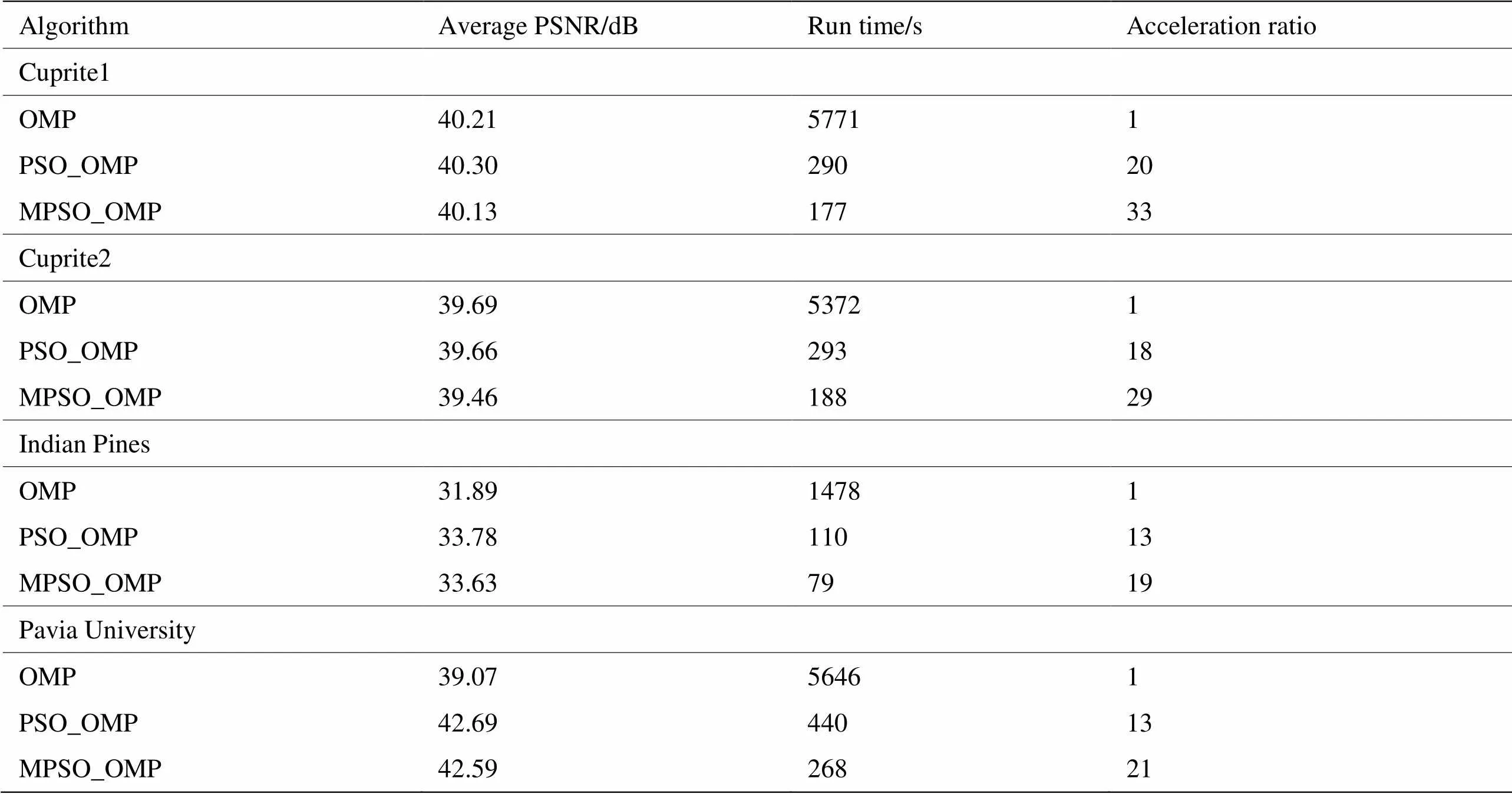
表2 OMP、PSO_OMP和MPSO_OMP的性能对比

算法PSO_OMP的重构PSNR与OMP算法的PSNR相当或略高于后者，这充分说明，利用粒子群的进化过程可以模拟OMP算法的匹配过程，搜索得到最优原子并实现图像的稀疏分解。因粒子群算法具有随机性，每次分解得到的原子可能并不是最优的，在保证相同重构精度的条件下，最优原子个数要多于OMP算法所需搜索的原子个数。但从计算复杂度分析，PSO_OMP算法具有较大的优势，与OMP算法相比，运行时间能降低一个数量级，计算效率提高10倍以上。

对场景Cuprite 1和Cuprite 2，利用算法MPSO_OMP得到的重构PSNR与OMP算法的PSNR相当。这充分说明，在对非参考波段图像进行稀疏分解时，从参考波段图像的最优原子集合中继承部分原子的方法能够表示图像的共性特征，利用谱间相关性对PSO_OMP进行改进具有可靠性。与粒子群搜索过程的计算复杂度相比，继承原子的选择过程耗时较少，因此这种改进方法能更进一步地降低整个稀疏分解过程的计算复杂度。对于场景Indian Pines来说，利用PSO_OMP算法和MPSO_OMP算法均能保证重构精度，与PSO_OMP算法相比，MPSO_OMP算法能够进一步地提高稀疏分解效率。但因Indian Pines数据的谱间相关性要弱于其他3组高光谱数据，因此MPSO_OMP的加速最不明显。对于场景Pavia University来说，利用150个原子得到的重构图像的PSNR要高出利用50个原子得到的重构PSNR，且运算效率有显著提高。

数据集Cuprite1经过稀疏分解后，重构图像与原始图像的对比如图7所示，图中为原始图像和重构图像的第40个波段（该波段是非参考波段），并给出了相应的重构PSNR。对于场景Cuprite1来说，3种算法得到的重构PSNR相差无几，OMP算法、PSO_OMP算法和MPSO_OMP算法的重构PSNR分别能达到40.1143dB、40.1518dB和40.1194dB。重构图像能够很好地描述原始图像的细节特征，充分说明利用PSO算法去优化OMP算法的匹配过程非常可靠。PSO_OMP算法和MPSO_OMP算法得到的重构图像非常接近，说明继承原子能够表示图像的共性特征，而粒子群搜索的其他部分原子表示了图像的差异性，二者相互结合，共同完成图像的高精度稀疏分解，充分说明算法的有效性。

3 结论

提出了基于谱间相关性的稀疏分解算法，在利用粒子群优化对OMP算法匹配过程加速的基础上；考虑参考波段图像和非参考波段图像的谱间相关性，采用继承部分最优原子的方式改进非参考波段图像的最优原子搜索算法，进一步地提高稀疏分解效率。实验结果表明，与OMP算法及PSO_OMP算法相比，在保证重构精度的前提下，所提算法MPSO_OMP能够进一步有效地提高稀疏分解过程的计算效率。因粒子群算法存在一定的随机性，如何降低随机性对算法性能的影响将是下一步的工作方向。

[1] NIU Y, WANG B. Extracting Target Spectrum for hyperspectral target detection: an adaptive weighted learning method using a self-completed background dictionary[J]., 2017, 55(3): 1604-1617. (DOI: 10.1109/TGRS.2016.2628085)

[2] 蔡庆空, 李二俊, 蒋金豹, 等. 联合光谱-空间信息的短波红外高光谱图像茶叶识别模型[J]. 光谱学与光谱分析, 2019, 39(8): 2522-2527.

CAI Q, LI E, JIANG J, et al. Study on the tea identification of near-infrared hyperspectral image combining spectra-spatial information[J]., 2019, 39(8): 2522-2527.

[3] 陈善学, 周艳发, 漆若兰. 基于核函数的联合稀疏表示高光谱图像分类[J]. 系统工程与电子技术, 2018, 40(3): 692-698. (DOI: 10.3969 /j.issn. 1001-506X).

CHEN S, ZHOU Y, QI R. Joint sparse representation of hyperspectral image classification based on kernel function[J]., 2018, 40(3): 692-698. (DOI: 10.3969 /j.issn. 1001- 506X).

[4] FANG L, HE N, LI S, et al. A new spatial-spectral feature extraction method for hyperspectral images using local covariance matrix representation[J]., 2018, 56(6): 3534-3546. (DOI: 10.1109/ TGRS.2018.2801387).

[5] 张淳民, 穆廷魁, 颜廷昱, 等. 高光谱遥感技术发展与展望[J]. 航天返回与遥感, 2018, 39(3): 104-114. (DOI:10.3969/j.issn.1009-8518).

ZHANG C, MU T, YAN T, et al. Overview of hyperspectral remote sensing technology[J]., 2018, 39(3): 104-114. (DOI:10.3969/j.issn.1009-8518).

[6] CHANG C I. A review of virtual dimensionality for hyperspectral imagery[J]., 2018, 11(4): 1285-1305. (DOI: 10.1109 /JSTARS. 2017.2782706).

[7] 唐中奇, 付光远, 陈进, 等. 基于低秩结构提取的高光谱图像压缩表示[J]. 电子与信息学报, 2016, 38(5): 1085-1091.

TANG Z, FU G, CHEN J, et al. Low-rank structure based hyperspectral compression representation[J]., 2016, 38(5): 1085-1091.

[8] 马馨宏, 郭树旭. 高光谱遥感图像的稀疏分解与压缩感知[J].吉林大学学报: 理学版, 2015, 53(4): 767-772.

MA X, GUO S. Compressed sensing and sparse decomposition of hyperspectral imgae[J].: Science Edition, 2015, 53(4): 767-772.

[9] GUO K, XIE X, XU X, et al. Compressing by learning in a low-rank and sparse decomposition form[J]., 2019, 7: 150823-150832.

[10] 王忠良, 冯文田, 粘永健. 结合光谱解混与压缩感知的高光谱图像有损压缩[J]. 红外与激光工程, 2018, 47(S1): 197-204.

WANG Z, FENG W, NIAN Y. Compressive- sensing-based lossy compression for hyperspectral images using spectral unmixing[J], 2018, 47(S1): 197-204.

[11] YAO L, DU X. Identification of underwater targets based on sparse representation[J]., 2020(8): 215-228.

[12] TAN Shoubiao, SUN Xi, CHAN Wentao, et al. Robust face recognition with kernelized locality-sensitive group sparsity representation[J]., 2017, 26(10): 4661-4668.

[13] PAN L, LI H C, MENG H, et al. Hyperspectral image classification via low-rank and sparse representation with spectral consistency constraint [J]., 2017, 14(11): 2117-2121.

[14] 任智伟, 吴玲达. 基于本征图像分解的高光谱图像空谱联合分类[J]. 航天返回与遥感, 2019, 40(3): 111-120. (DOI:10.3969/j.issn.1009- 8518).

REN Z, WU L. Spectral-spatial classification for hyperspectral imagery based on intrinsic image decomposition[J]., 2019, 40(3): 111-120. (DOI:10.3969/j.issn.1009-8518).

[15] SONG X, WU L and HAO H. Hyperspectral image denoising base on adaptive sparse representation[C]//2018(DSC), 2018: 735-739.

[16] MEI S, HOU J, CHEN J, et al. Simultaneous spatial and spectral low-rank representation of hyperspectral images for classification[J]., 2018, 56(5): 2872-2886.

[17] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]., 2007, 53(12): 4655-4666.

[18] Kulkarni A, Mohsenin T. Low overhead architectures for OMP compressive sensing reconstruction algorithm[C]//I:, 2017, 64(6): 1468-1480.

[19] CHEN S, DONOHO D, Saunders M. Atomic decomposition by basis pursuit[J]., 1999, 20: 33- 61.

[20] 王丽, 冯燕. 基于粒子群优化的图像稀疏分解算法研究[J]. 计算机仿真, 2015, 32(11): 363-367.

WANG L, FENG Y. Sparse decomposition of images based on particle swarm optimization[J]., 2015, 32(11): 363-367.

[21] 王丽, 冯燕. 基于空谱联合的多假设预测高光谱图像压缩感知重构算法[J]. 电子与信息学报, 2015, 37(12): 3000-3008.

WANG L, FENG Y. Compressed sensing reconstruction of hyperspectral images based on spatial-spectral multihypothesis prediction[J]., 2015, 37(12): 3000-3008.

Sparse Decomposition of Hyperspectral Images Based on Spectral Correlation

WANG Li，WANG Wei，LIU Boni

(Department of Electronic Engineering, Xi'an Aeronautical University, Xi'an 710077, China)

Considering the strong correlation between adjacent band images of hyperspectral data in combination with the fast searching ability of the particle swarm optimization algorithm, a sparse decomposition algorithm of hyperspectral images based on spectral correlation is proposed. The hyperspectral images are divided into reference and common band images. Particle swarm optimization is performed on the reference band images to find the optimal atoms and realize their sparse decomposition. The optimal atoms of a common band image consist of two parts. Parts of these atoms are inherited from the optimal atoms of the reference band images, and the number of inheritances is determined by the spectral correlation between the common and reference band images. The remaining atoms are obtained using particle swarm optimization. The experimental results on hyperspectral data show that in cases with the same reconstruction accuracy, the sparse decomposition rate is approximately 18 times higher than the orthogonal matching pursuit algorithm.

sparse decomposition, spectral correlation, particle swarm optimization, orthogonal matching pursuit, hyperspectral image

TP301.6

A

1001-8891(2020)10-0969-09

2020-03-22；

2020-09-29.

王丽（1987-），女，讲师，博士，主要研究方向为高光谱图像处理、优化算法研究，E-mail：wangli871016@163.com。

国家自然科学基金项目（61901350）；陕西省教育厅专项科研计划项目（19JK0432）；西安航空学院校级科研基金（2019KY0208）。