基于RBF网络的红外多光谱辐射测温

席剑辉，姜 瀚

〈测量技术〉

基于RBF网络的红外多光谱辐射测温

席剑辉，姜 瀚

（沈阳航空航天大学 自动化学院，辽宁 沈阳 110136）

在目标发射率未知的情况下，建立一种基于RBF（radial basis function）神经网络的红外测温方法。首先推导出目标温度同辐射亮度峰值及其波长之间的强非线性关系，明确神经网络输入变量；然后基于RBF网络对样本数据进行充分学习，建立目标辐射测温模型，该模型不需要发射率输入。利用黑体和钢板目标分别作为测试目标源，验证这种方法，得到黑体测温最大相对误差为0.016%、钢板的最大相对误差为1.08%，验证了本文测温方法的合理性。

辐射亮度；多光谱测温；RBF网络

0 引言

温度的准确测量与有效控制在国防、农业、医学、科技等领域有十分重要的作用[1]。红外辐射测温原理通常基于测得的目标热辐射通量，根据目标发射率，推算目标温度，所以红外测温不可避免要研究目标的发射率情况[2]。在目标发射率已知的情况下可以应用亮度测温法和全辐射测温法。亮度测温法是分别测量目标和黑体在给定波长下的辐射亮度值，令这两个亮度值相等，此时黑体的温度称为亮温，再根据亮温和发射率可以求得目标的温度[3]。全辐射测温法[4]通过测量目标整个波段的辐射能量，然后依据斯蒂芬玻尔兹曼定律计算出目标温度。在目标发射率未知情况下，可以应用比色测温法、光谱极值测温法以及多光谱测温法进行测温。比色测温法是通过测量两个给定波长的辐射能量之比，利用黑体炉对仪器进行标定，进而计算色温[5-6]。比色测温法的优点是可以消除一部分环境因素的影响；缺点是当两个给定波长处发射率发生变化时，会产生很大的误差。光谱极值测温法是依据维恩定律，黑体辐射亮度曲线峰值点处对应的波长与黑体温度的乘积是固定常数，通过对辐射亮度曲线一阶求导，得出峰值点处的波长，进而计算出目标的温度[7]。虽然光谱极值测温法原理非常简单，但是它存在着测量目标只能近似灰体以及峰值点不能处震荡波段的局限性。光谱极值法需要将发射率近似为常数不变。多光谱测温法[8-9]首先假设目标光谱发射率与波长之间存在着某种函数关系模型，然后将假设的发射率模型替换普朗克定律中的发射率，进而计算目标温度。在应用多光谱测温法时，如果假设的这种函数关系与实际不相符，那么得到的测温结果误差会很大。

在实际测量过程中，很多时候测量目标的发射率都是未知的。在这种情况下，利用神经网络测温的优点是不需要像多光谱测温法那样假设发射率与波长之间函数关系模型[10-11]；也不需要像光谱极值法那样将发射率近似为常数不变；更不必像比色测温法在给定两个波长处发射率做近似不变处理[12]。它是直接通过测量目标在不同温度下的多组辐射亮度曲线，利用辐射亮度曲线峰值点处波长、亮度值与温度之间映射关系来建立测温模型。而且即使光谱辐射亮度曲线峰值点处在水蒸气和二氧化碳吸收带波段或者震荡波段时，这种方法同样适用。

1 目标辐射温度建模

根据普朗克定律以及发射率定义，可以得出目标在温度时的光谱辐射亮度(,)为：

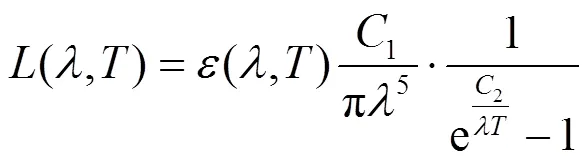
式中：1、2分别为第一辐射常数、第二辐射常数。

当2/≫1，可得维恩近似公式：

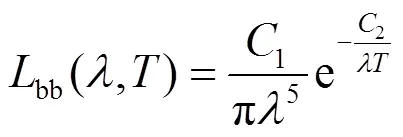
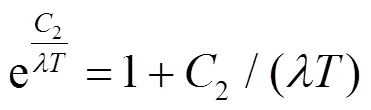
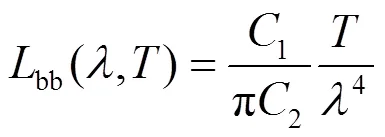
式中：bb(,)为黑体在波长和温度时的光谱辐射亮度。

结合发射率定义，当2/≫1时，目标的光谱辐射亮度近似为：

将式(4)移项整理后对波长求导，得：

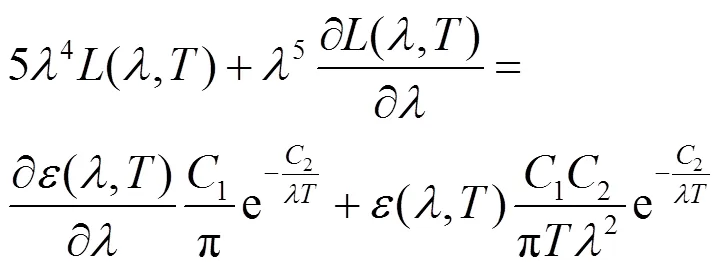
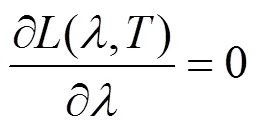
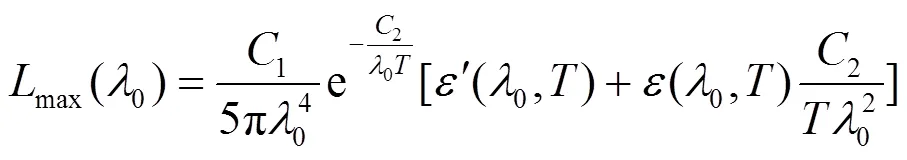
式中：峰值点处的光谱发射率(0,)与峰值点处光谱发射率的导数¢(0,)只与温度有关。所以，温度与峰值点处波长0和亮度值max(0)之间存在强非线性。

同理，当2/＝1时，目标的光谱辐射亮度近似为：

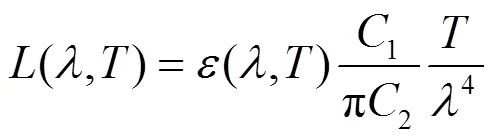
将式(7)移项整理得：

将式(8)对波长求导，得：

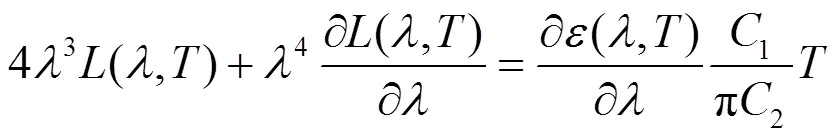
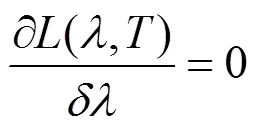
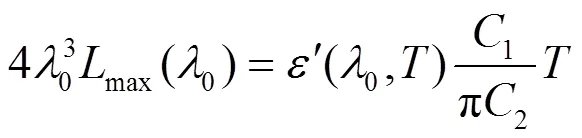
式中：峰值点处光谱发射率的导数¢(0,)只与温度有关。由(6)式和式(10)可以看出，目标的温度为峰值点处波长0和亮度值max(0)的隐式函数，具有强非线性，用常规建模方法难以解决。

神经网络具有能够逼近任意非线性函数的特点，在不需要具体知道系统模型和动态特性的基础上就能通过有效的样本学习，获得内在的规律[13]，对式(6)和式(10)无法用具体的数学模型表达的非线性函数关系尤其有效。RBF神经网络具备很强的非线性拟合能力，可以映射任意复杂的非线性关系，学习规则简单，计算机容易实现。综上所述，测温模型的结构框图可以设计如图1。

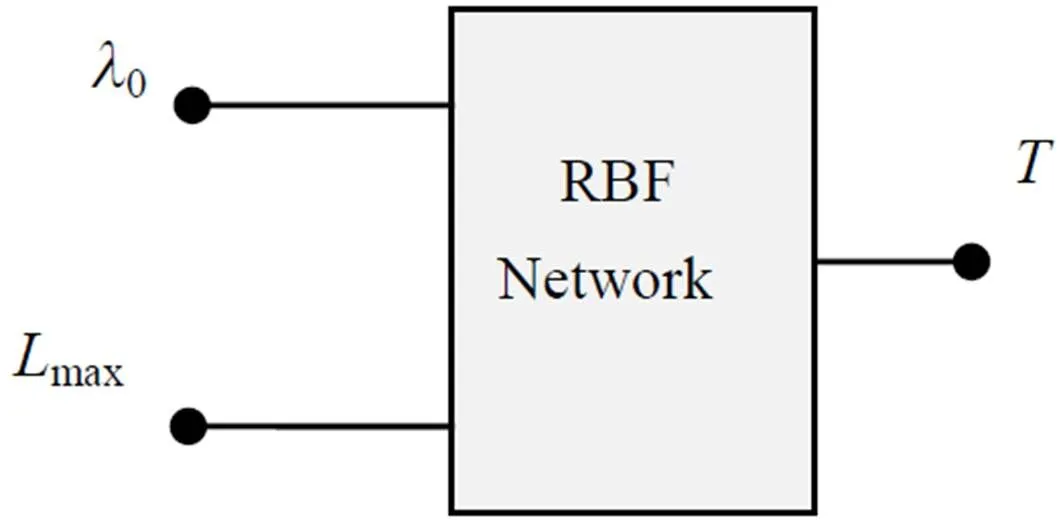
图1 测温模型结构框图

当温度为时，网络的输入端为辐射亮度曲线峰值点处波长0、亮度值max(0,)，输出为温度。

2 RBF神经网络红外光谱测温方法

RBF（radial basis function）神经网络的结构如图2所示，是一种由输入层、隐含层和输出层组成的3层神经网络。从输入空间到隐层空间的变换是非线性的，而从隐层空间到输出层空间的变换是线性的[14]。

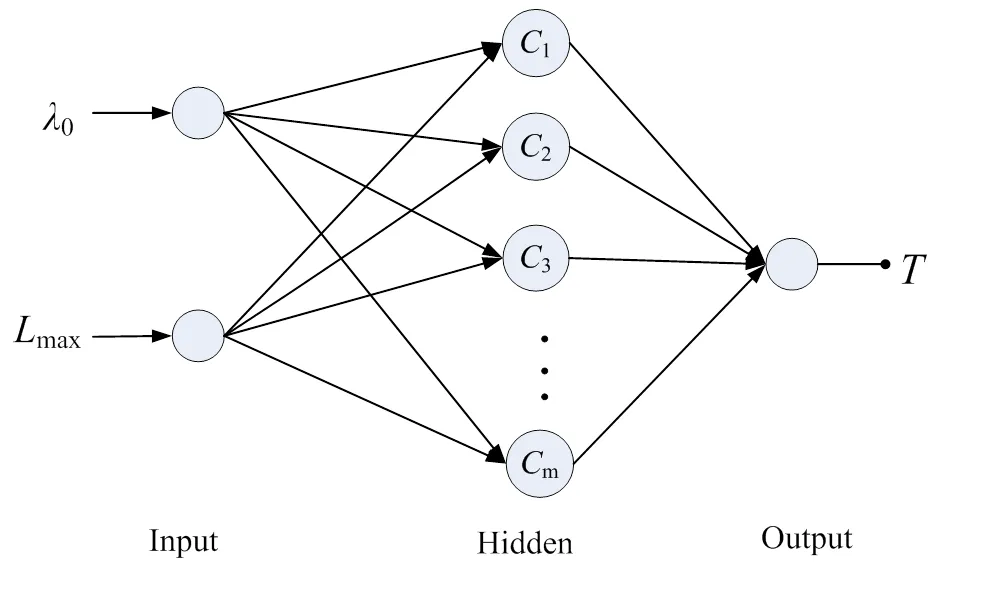
图2 RBF网络结构图

输入层空间到隐含层空间的映射关系与所选择的径向基函数()有关，这里选取Gauss函数作为隐含层径向基函数如公式(9)。隐含层空间到输出层空间的映射关系与对应的权值有关。当温度为时，令网络的输入为为峰值点处的波长和亮度值，网络输出为，假定隐层单元个数为1，那么隐含层第个单元的输出为：

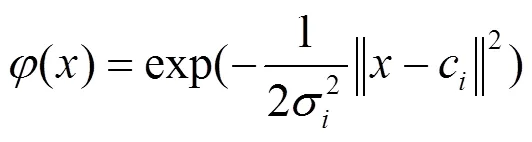
式中：＝1, 2, …,1；c为第个单元的聚类中心；为宽度系数。网络的输出为：

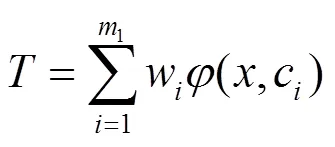
式中：w为第个隐层单元到网络输出的权值。

网络的残差：

＝实－(13)

式中：实为真实温度。

通过对网络输入输出样本的学习，训练网络的过程中要解决结构设计问题和权值修正问题。

RBF网络的建模步骤如下：

1）对网络进行初始化设置，在样本集中随机选取1个训练样本作为聚类中心c，＝1, 2, …,1。

2）根据上一步选定的RBF中心，利用公式(12)求宽度系数。

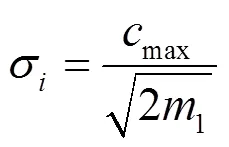
式中：max为当前聚类中心之间的最大距离。

4）按照公式(12)计算网络的输出，利用最小二乘法确定隐含层到输出层的权值w，＝1, 2, …,1。

3 实例

实验采用的仪器为加拿大ABB BOMEN的MR170型的光谱辐射计（如图3所示），光谱分辨率为1～32cm－1，分别测量黑体和涂有航空材料涂层的钢板目标在3～12mm波段的多光谱红外辐射特性，温度范围为80℃～180℃。

图3 光谱辐射计

3.1 黑体测温及验证

理想黑体的光谱发射率是一个常数，本文实验所测量的黑体发射率真实值0.98。实验测得41组黑体在不同温度下的辐射亮度曲线，对震荡波段亮度曲线进行校准处理后整理出峰值点处波长和亮度值如表1所示。

在黑体的41组样本数据中，在不同温段随机选取7组样本数据作为测试样本，剩余的34组样本数据当作训练样本数据，为验证方法有效性，采用不同的验证样本和训练样本，进行3次仿真实验。训练RBF神经网络，输入测试样本得到3次仿真结果如图4所示。

图4中横轴代表的是黑体测试的样本点，纵轴代表的是黑体测试样本的温度，“*”线表示的是黑体测试样本的实际温度，“o”线表示的是黑体测试样本RBF网络的输出温度m。可以看出网络的输出温度与样本的实际温度非常接近、基本重合。7个测试样本点的测温结果以及相对误差如表2所示。

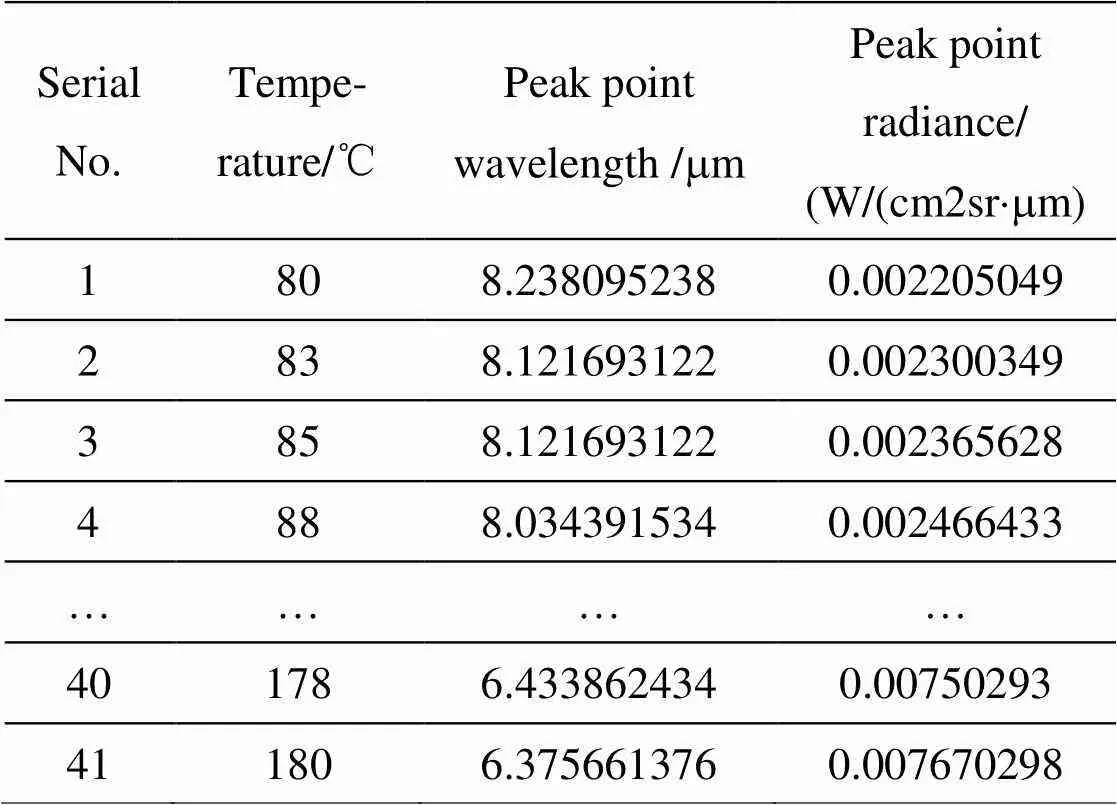
表1 黑体在不同温度下峰值点处波长和亮度值部分数据

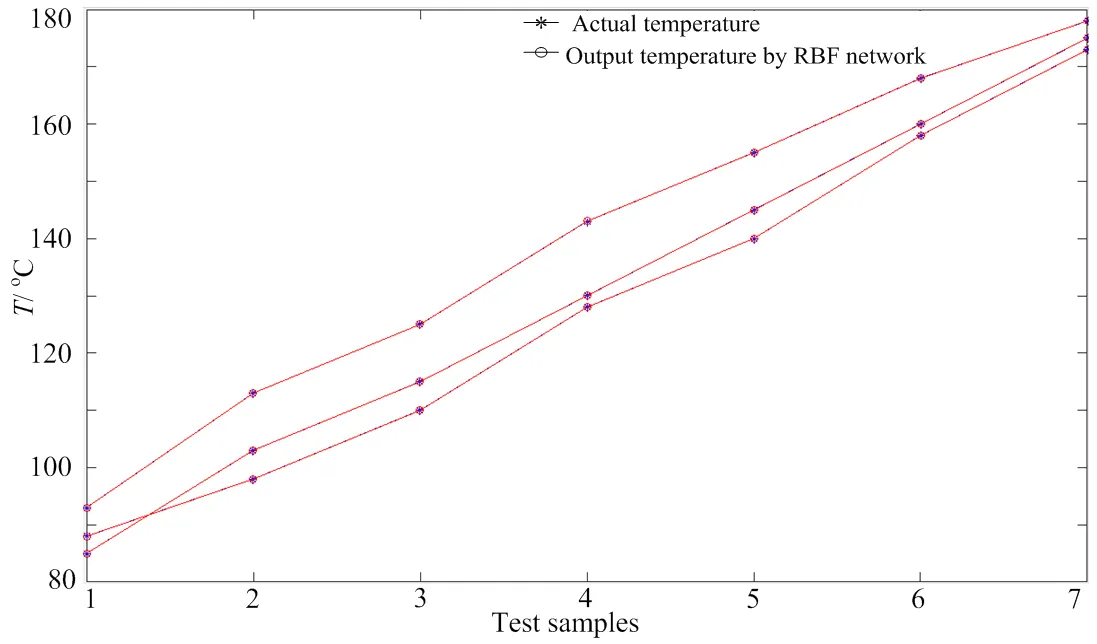
图4 黑体测温仿真结果

从表2中可以看出，在不同温段随机选取黑体的7个测试样本点在3次实验中得到的测温结果相对误差都很小，最大相对误差只有0.016%，说明测量结果精度很高，可以利用这种方法对未知目标进行测温。

3.2 目标钢板测温及验证

通过上文黑体的实验结果，验证了本文方法可以测量未知发射率目标的温度，而且测量结果误差很小。现将本文的方法应用于某型飞机上的一块钢板的温度估计，该钢板表面具有涂层（如图5所示），连接加热片，通过外接控制器控制钢板的温度，利用光谱辐射计测量目标钢板的辐射特性。

实验测得目标钢板在不同温度下辐射亮度曲线共41组，整理出峰值点处波长和亮度值如表3。

在目标钢板的41组样本数据中，不同温段随机选取7组样本数据作为测试样本，剩余的34组样本数据当作训练样本数据，一共进行3次不同的选取实验。训练RBF神经网络后，得到3次仿真结果如图6所示。

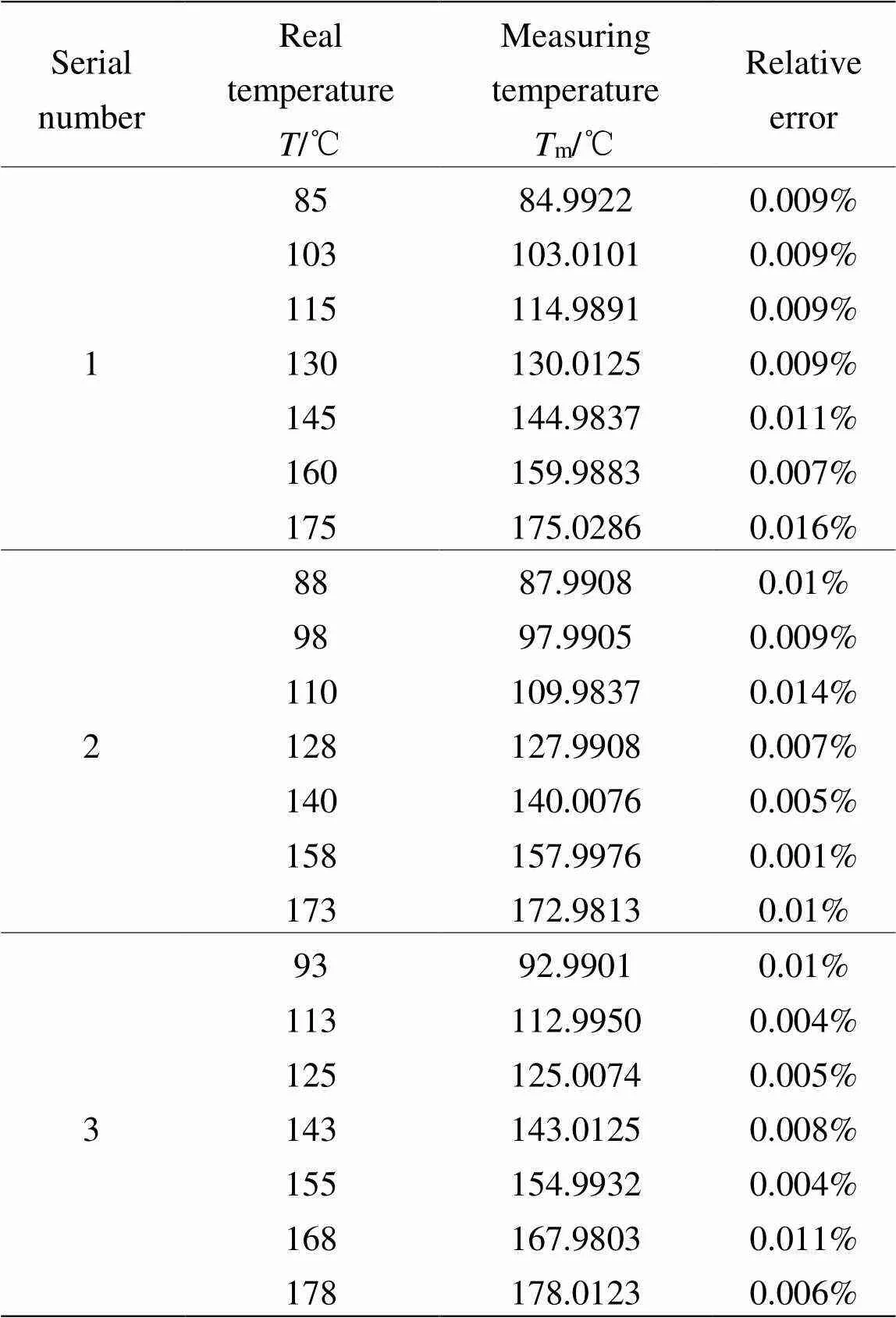
表2 黑体的测温结果

图5 目标钢板

图6中横坐标代表的是测试的样本点，纵坐标代表温度，“*”线表示的是目标钢板测试样本的实际温度，“o”线表示的是目标钢板测试样本RBF网络的输出温度m。从图中可以看出网络的输出温度与样本的实际温度很相近、比较吻合。7个测试样本的相对误差如表4所示。

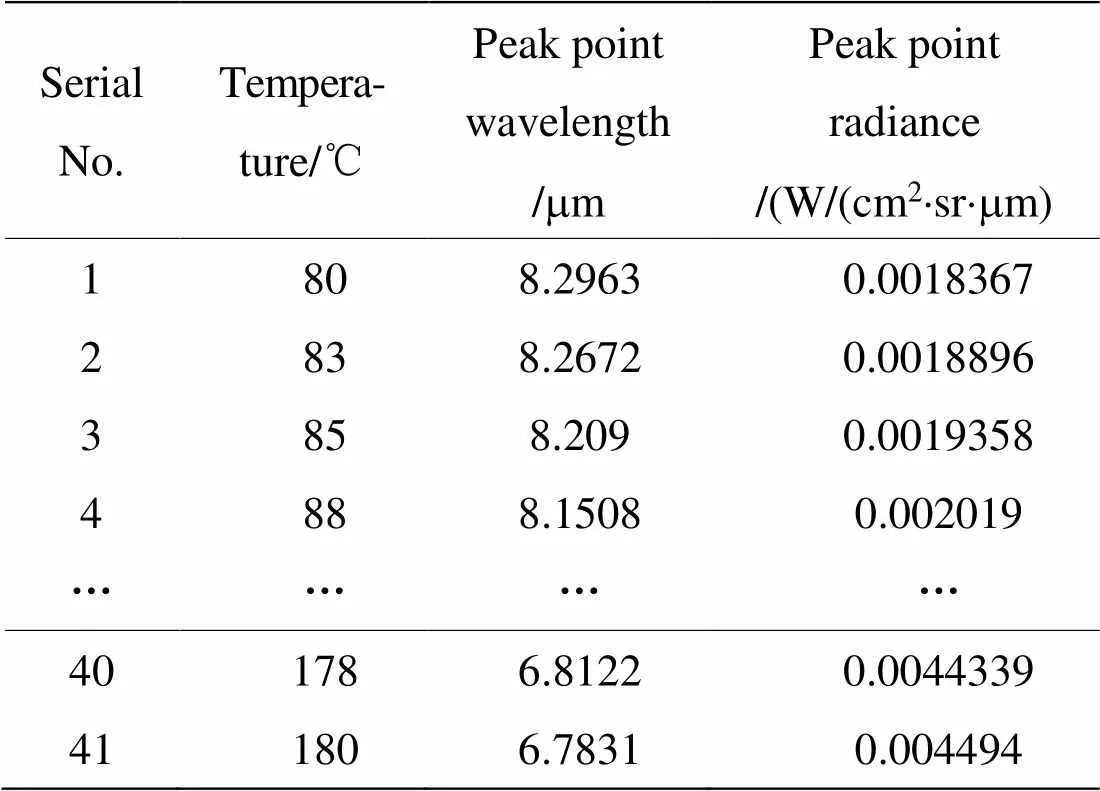
表3 目标钢板在不同温度下峰值点处波长和亮度值部分数据

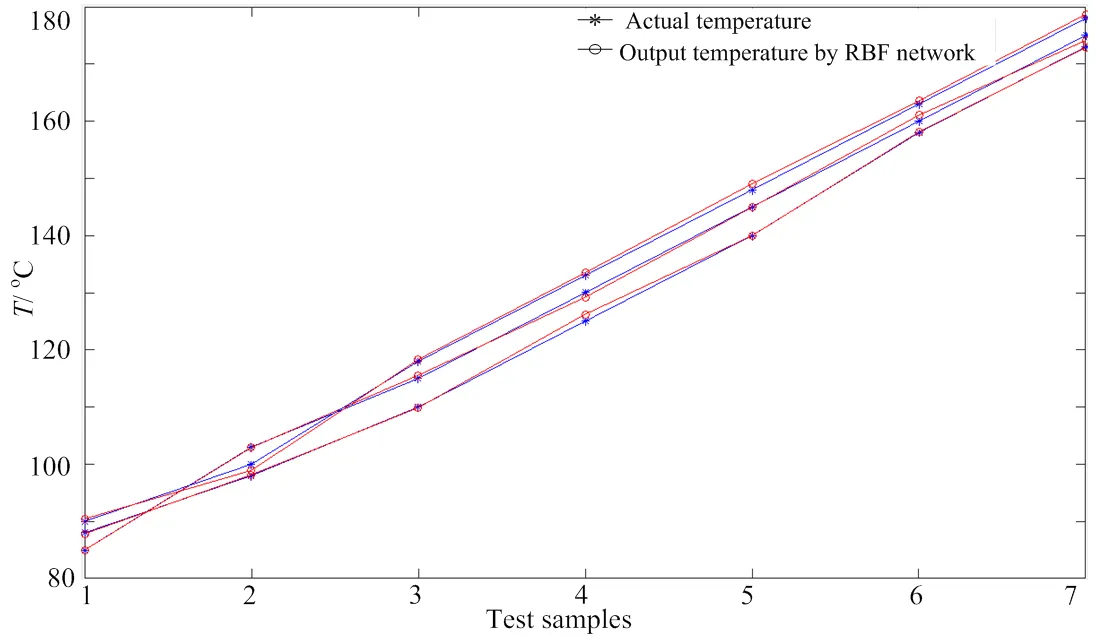
图6 钢板测温仿真结果

从表4中可以看出目标钢板在3次实验中，7个测试样本测温结果的相对误差都不大，而且最大相对误差只有1.08%，表明了这种测温方法精度很高，也验证了方法的合理性。

4 结论

本文提出了一种未知发射率的目标红外辐射温度测量方法。通过推导建立目标温度与辐射亮度曲线峰值及峰值波长的非线性模型；进而引入RBF神经网络并确定网络输入变量，利用网络的强非线性自适应学习能力建立测温模型。用黑体和具有隐身涂层的钢板分别作为测试目标进行测温实验。得到黑体的测温结果相对误差最大为0.016%，带有隐身涂层钢板的测温结果最大相对误差为1.08%，两种测量目标的误差都很小，这说明了这种测温方法的合理性。

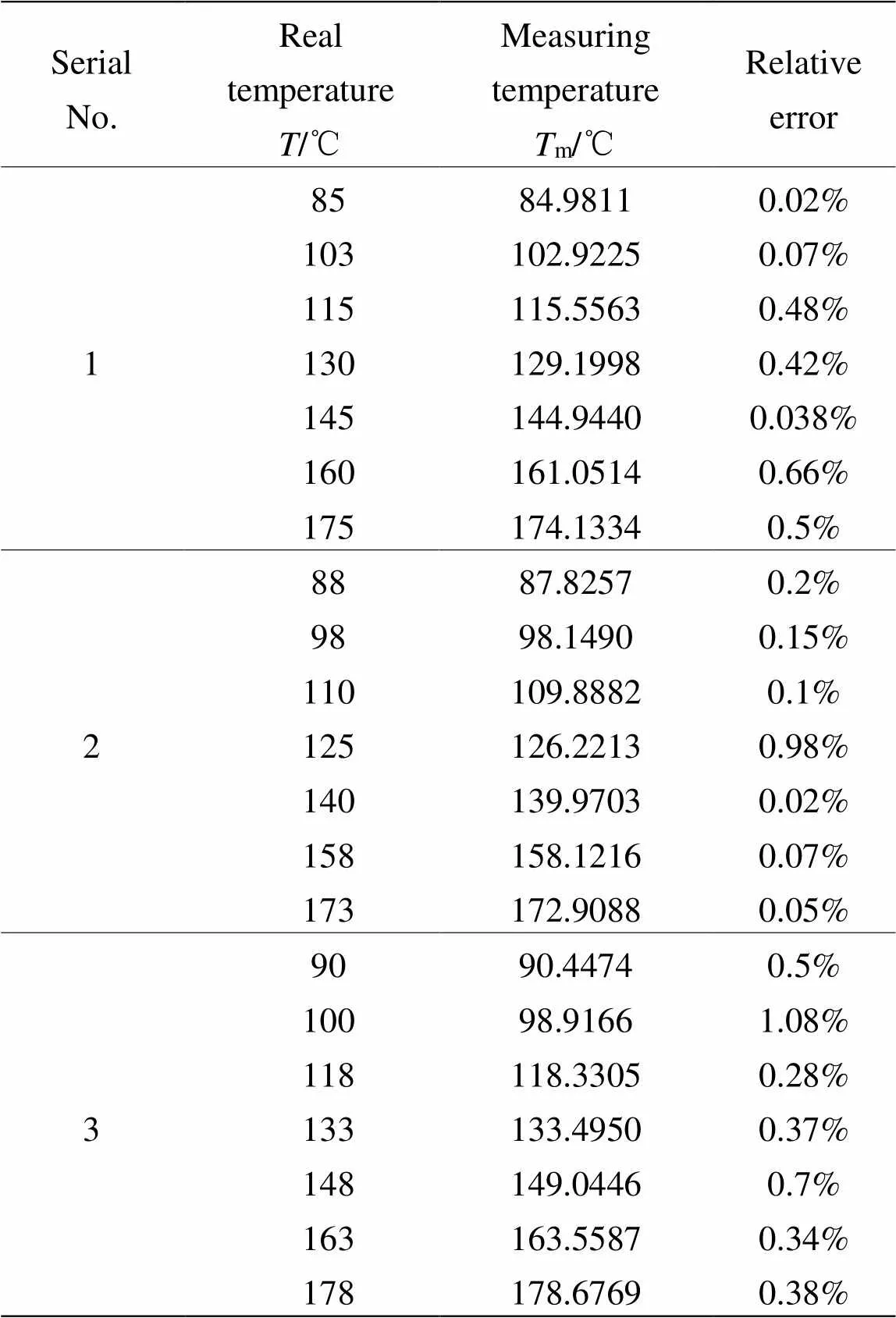
表4 钢板测温结果相对误差

[1] 戴景民. 辐射测温的发展现状与展望[J]. 自动化技术与应用, 2004, 24(3): 1-7.

DAI Jingmin. Development status and prospect of radiation temperature measurement[J]., 2004, 24(3): 1-7.

[2] 孙晓刚, 戴景民, 丛大成, 等. 多光谱辐射测温度理论研究[J]. 红外与毫米波学报, 1998, 17(3): 221-225.

SUN Xiaogang, DAI Jingmin, CONG Dacheng, et al. Theoretical study on multi-spectral radiation temperature measurement[J]., 1998, 17(3): 221-225.

[3] 原遵东. 辐射测温度广义有效亮度温度[J]. 仪器仪表学报, 2012, 33(4): 721-726.

YUAN Zundong. Generalized effective luminance temperature for radiometric temperature measurement[J]., 2012, 33(4): 721-726.

[4] 陈一明. 红外热像仪测温精度的研究[D]. 河北: 燕山大学, 2017.

CHEN Yiming. Study on Temperature Measurement Accuracy of Infrared Thermography[D]. Hebei: Yanshan University, 2017.

[5] 孙元, 彭小齐. 基于彩色CCD的双色与三色比色测温法比较研究[J]. 传感技术学报, 2015, 28(8): 1184-1187.

SUN Yuan, PENG Xiaoqi. Comparative study of two-color and three -color colorimetric temperature measurement based on color CCD [J]., 2015, 28(8): 1184-1187.

[6] 曹立华, 杨词银, 万春明. 基于校准的双波段比色测温法[J]. 仪器仪表学报, 2012, 33(8): 1882-1888.

CAO Lihua, YANG Ciyin, WAN Chunming. Two-band colorimetric temperature measurement based on calibration[J]., 2012, 33(8): 1882-1888.

[7] 王新北, 萧鹏, 戴景民. 基于傅里叶红外光谱仪的光谱发射率测量装置的研制[J].红外与毫米波学报, 2007, 26(2): 149-152.

WANG Xinbei, XIAO Peng, DAI Jingmin. Development of spectral emissivity measurement device based on Fourier infrared spectrometer [J]., 2007, 26(2): 149-152.

[8] 孙晓刚, 李成伟, 戴景民, 等. 多光谱辐射测温理论综述[J].计量学报, 2002, 23(4): 248-286.

SUN Xiaogang, LI Chengwei, DAI Jingmin, et al. A review of the theory of multispectral radiation temperature measurement [J]., 2002, 23(4): 248-286.

[9] 张磊. 基于光谱识别的多光谱测温技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.

ZHANG Lei. Research on Multi-spectral Temperature Measurement Based on Spectral Recognition[D]. Harbin: Harbin Institute of Technology, 2016.

[10] Duvaut T, Georgeault D, Beaudoin J. Multi-wavelength infrared pyrometry: optimization and computer simulations[J]., 1995, 36(7): 1089-1103.

[11] SUN X G, YUAN G B, DAI J M, et al. Processing method of multi- wavelength pyrometer data for continuous temperature measure- ments[J]., 2005, 26(4): 1255-1261.

[12] 邢冀川, 刘广荣, 金伟其, 等. 双波段比色测温方法及其分析[J]. 红外技术, 2002, 24(6): 73-76.

XING Jichuan, LIU Guangrong, JIN Weiqi, et al. Dual-band colorimetric temperature measurement method and its analysis[J]., 2002, 24(6): 73-76.

[13] 席剑辉, 徐振芳, 傅莉, 等. 红外辐射亮度的RBF网络建模及其光谱发射率估计[J]. 红外与激光工程, 2016, 45(s1): 24-29.

XI Jianhui, XU Zhenfang, FU Li, et al. RBF network modeling of infrared radiation luminance and its spectral emissivity estimation[J]., 2016, 45(s1): 24-29.

[14] 刘砚菊, 寇国豪, 宋建辉. 基于RBF神经网络的空中目标识别技术[J]. 火力与指挥控制, 2015, 40(8): 9-13.

LIU Yanju, KOU Guohao, SONG Jianhui. Aerial target recognition technology based on RBF neural network [J]., 2015, 40(8): 9-13.

Infrared Multispectral Radiation-Temperature Measurement Based on RBF Network

XI Jianhui，JIANG Han

(School of Automation, Shenyang Aerospace University, Shenyang 110136, China)

An infrared temperature-measurement method based on a radial basis function (RBF) neural network is established in the case of unknown target emissivity. First, the strong nonlinear relationship between the target temperature and the peak of the radiance curve and its wavelength is derived. The inputs to the neural network are determined. Then, according to the RBF network, sample data are studied, and a target radiation-temperature-measurement model is established. The model does not require emissivity. A blackbody and steel plate target are used as test targets to prove the proposed method. The maximum relative error of the temperature of the blackbody is 0.016% and that of the steel plate is 1.08%. These results verify the rationality of the established temperature-measurement method.

radiance, multispectral thermometry, RBF network

TN219

A

1001-8891(2020)10-0963-06

2019-06-10；

2019-09-18.

席剑辉（1975-），女，辽宁沈阳人，副教授，博士，主要研究方向为复杂系统模型辨识、故障检测与诊断、红外辐射测试与分析等。E-mail：85782853@qq.com。

国家自然科学基金青年基金资助项目（61503256）；辽宁省自然科学基金项目（2015020069，2015020061），沈阳市科技创新团队项目（src201204）。