一种风驱动优化Tsallis相对熵的图像多阈值分割方法

李粉红，卢 晶，张志光

一种风驱动优化Tsallis相对熵的图像多阈值分割方法

李粉红1，卢 晶1，张志光2

（1. 商洛学院 数学与计算机应用学院，陕西 商洛 726000；2. 北京工业大学 信息与通信工程学院，北京 100124）

本文提出了一种风驱动优化Tsallis相对熵的图像多阈值分割算法。首先分析了Tsallis相对熵阈值分割原理，并将其推广到多阈值分割。利用高斯分布拟合分割后的图像直方图信息，利用Tsallis相对熵作为衡量最佳分割阈值的度量函数。将风驱动优化算法与Tsallis相对熵度量函数结合，求解Tsallis相对熵函数的最优解，提高阈值分割算法的速度。最后将所提算法与穷举法、粒子群算法做比较，并且与经典的Otsu算法和基于二维熵的多阈值分割法进行对比。实验结果表明所提算法速度快、准确性高能够用于图像的多阈值分割。

图像分割；Tsallis相对熵；高斯分布；风驱动优化；粒子群

0 引言

图像分割被应用在各个领域，如医学图像，工业机器视觉，缺陷检测等。图像分割的主要目的是将图像中感兴趣的区域如图像中的前景等分割出来[1-5]。

图像阈值化的关键在于通过一定的准则找到最优阈值，并且通过最优阈值对图像进行分割。目前阈值分割方法多种多样，按照作用范围可以分为全局阈值法和局部阈值法；依据阈值选取准则可以分为：最大熵法，类间方差法，交叉熵法，最小误差法，模糊熵法等等。按照阈值个数可以分为单阈值分割方法和多阈值分割方法等。按照直方图维数来分，可以分为一维直方图法，二维直方图法等等[6-10]。

为了解决分割随着阈值的增加分割所需计算量成倍数增长即耗时长的问题。很多学者将分割方法与群智能优化算法相结合来提高图像的分割速度。目前常见的用于图像分割的群智能算法的包括：粒子群、人工蜂群、遗传算法等等[11-14]。但由于这些算法有时会陷入局部最优导致分割不准确。

风驱动优化算法（wind driven optimization algorithm, WDO）是一种新型群智能算法，具有较强的全局寻优性能。本文将Tsallis相对熵单阈值分割推广到Tsallis多阈值分割并与风驱动算法结合，提出了一种新的图像多阈值分割方法。将多阈值的值作为空气粒子单元、将Tsallis相对熵函数作为风驱动算法的适应度函数对相对熵函数进行最优求解，最终获取分割图像的最优阈值。

1 Tsallis相对熵多阈值图像分割原理

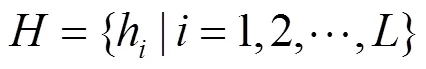
定义1到A＋1的类概率为：

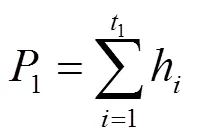
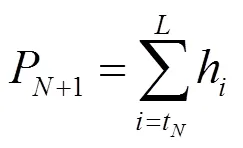
其中1+2+…+P+1=1。同时定义1～A＋1的灰度级类均值为：

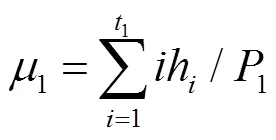
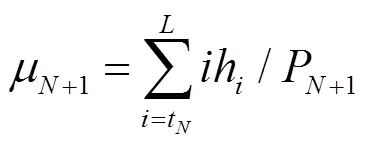
定义1到A＋1的灰度级类方差为：

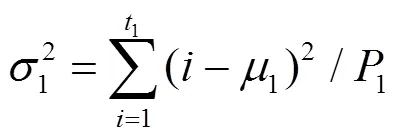
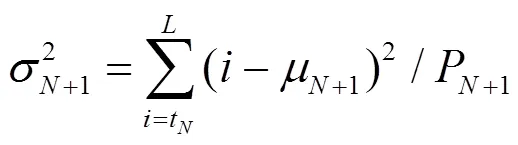
灰度级关于1到A＋1的类概率为：

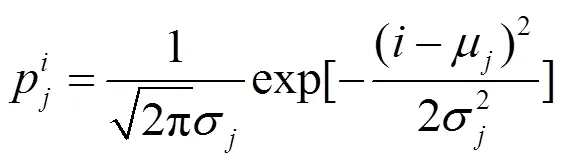
＝1,2,…,，＝1,2,…+1 (4)

定义分割后图像灰度级的拟合高斯分布为：

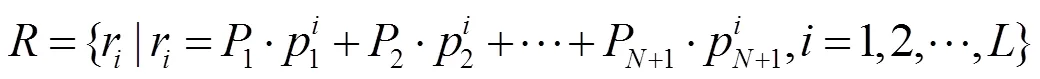
图像的阈值化准则即Tsallis相对熵函数：

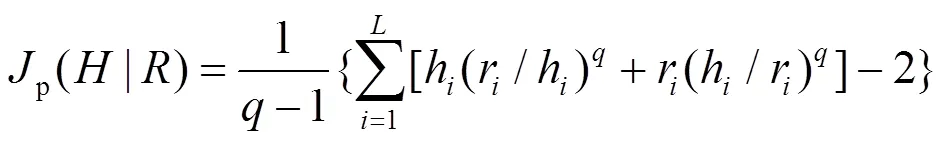
在对图像进行分割时，如果能够找到个分割阈值1,2,…,t，使式(6)值最小，则这些阈值为最优阈值，最佳分割阈值的集合的获取函数为：

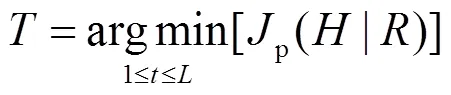
2 基于Tsallis相对熵与风驱动优化的图像多阈值分割算法

为了改善基于Tsallis相对熵多阈值图像分割方法计算量大、速度慢的问题，本文引入风驱动优化算法求解Tsallis相对熵函数的最优解。

2.1 风驱动优化算法

风驱动优化算法（WDO）[15-16]是一种自然启发算法，是一种新型全局优化算法。其原理是模拟自然界中风的流动，即空气之间存在压差促使空气流动，最终达到平衡的过程。空气粒子达到平衡的最终位置值即为每个空气粒子的最优解。风驱动优化算法的原理如下：

一个由个空气单元、维搜索空间组成的空气种群可以表示为如下矩阵：

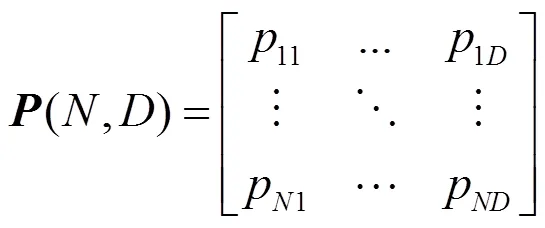
每个空气粒子有两个特征分别为空气粒子的速度、和空气粒子的位置。空气粒子的速度矩阵为和位置矩阵分别为：

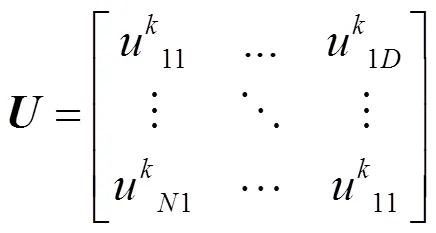
其中1≤≤IT，IT为最大迭代次数。风驱动优化算法的适应函数为Tsallis相对熵：

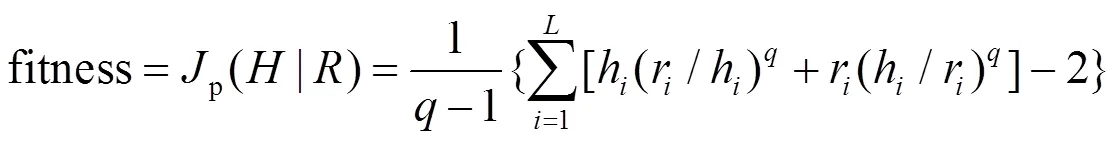
风驱动优化算法将影响大气运动的力：摩擦力、气压梯度压力、重力和科氏力带入牛顿第二定律结合理想气体状态方程得出速度更新方程。空气粒子速度和位置根据方程(11)、(12)更新：

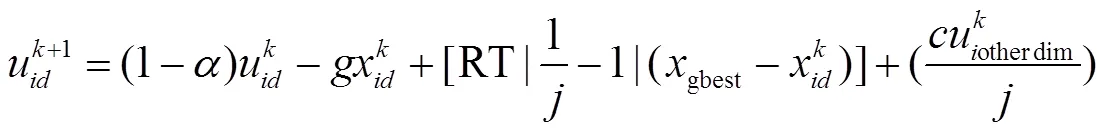
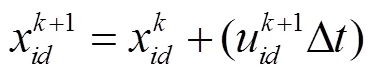
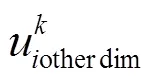
2.2 基于Tsallis相对熵与风驱动优化算法的图像多阈值分割

基于Tsallis相对熵与风驱动优化算法的图像多阈值分割算法的流程如图1所示。

主要步骤如下：

步骤1：输入待分割图像，根据设定阈值个数、随机初始化空气粒子数量、最大迭代步数，相应参数；

步骤2：根据Tsallis相对熵函数计算各个空气粒子的适应度值，并且排序；

步骤3：对每个空气粒子位置与其个体历史最优位置比较，记录个体历史最优位置；

步骤4：对每个空气粒子与总体历史最佳位置比较，记录总体最优位置；

步骤5：根据式(11)、(12)对空气粒子速度和位置进行更新；

步骤6：是否达到结束条件，如果达到则结束否则继续循环；

步骤7：将获得的阈值对图像进行分割得到分割后的最终图像。

3 实验结果与分析

为了验证本文所提方法在图像分割上的效果与计算速度优越性，本文算法在Matlab 2014a，Windows7、处理器主频为2.2GHz，内存2G的测试平台上运行。

3.1 本文算法对复杂图像的多阈值分割

本文对Camera、Lenna、Baboon、Lake这几幅经典图像进行分割。分别对图像进行单阈值、双阈值、三阈值、四阈值的分割。风驱动优化算法的相关参数设置如下：空气粒子数量为30，最大迭代次数为50次，空气粒子速度最大为3，RT的值为3，的值为0.3、的值为0.4，的值为0.4。Tsallis相对熵中的值为0.8。本文算法对各图像的分割结果如图2所示，从上往下依次为：Camera、Lenna、Baboon、Lake，从左往右依次为：原始图像、单阈值分割图像、双阈值分割图像、三阈值分割图像。

从图2中可以看出，本文算法的分割效果良好，能够对复杂图像进行多阈值分割，分割出来的部分边缘清晰，从图2(d)Lake中可以看到，随着阈值的增加，天空、云、树，湖这几者被有效地分割出来，且分割出来的部分边缘清晰，目标完整。

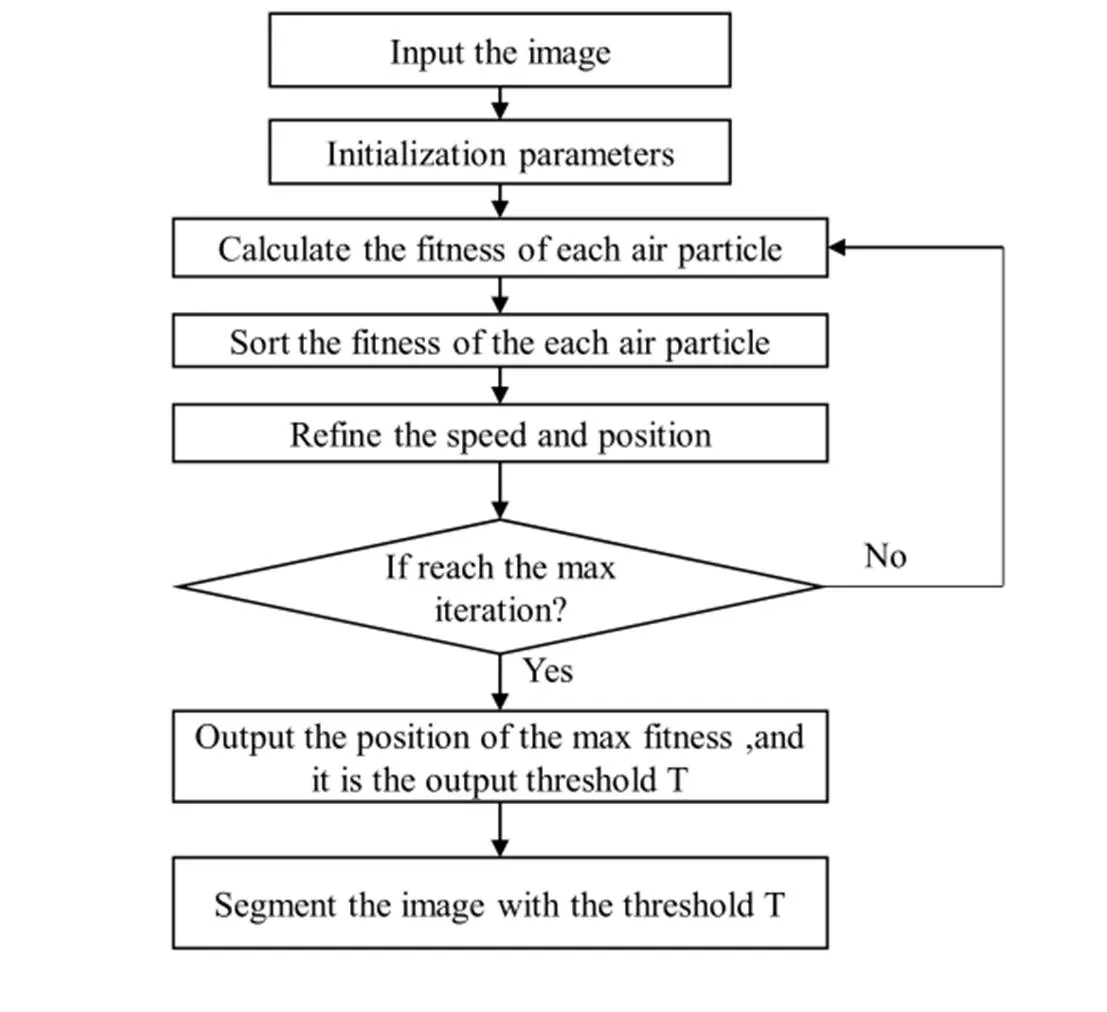
图1 本文算法流程图

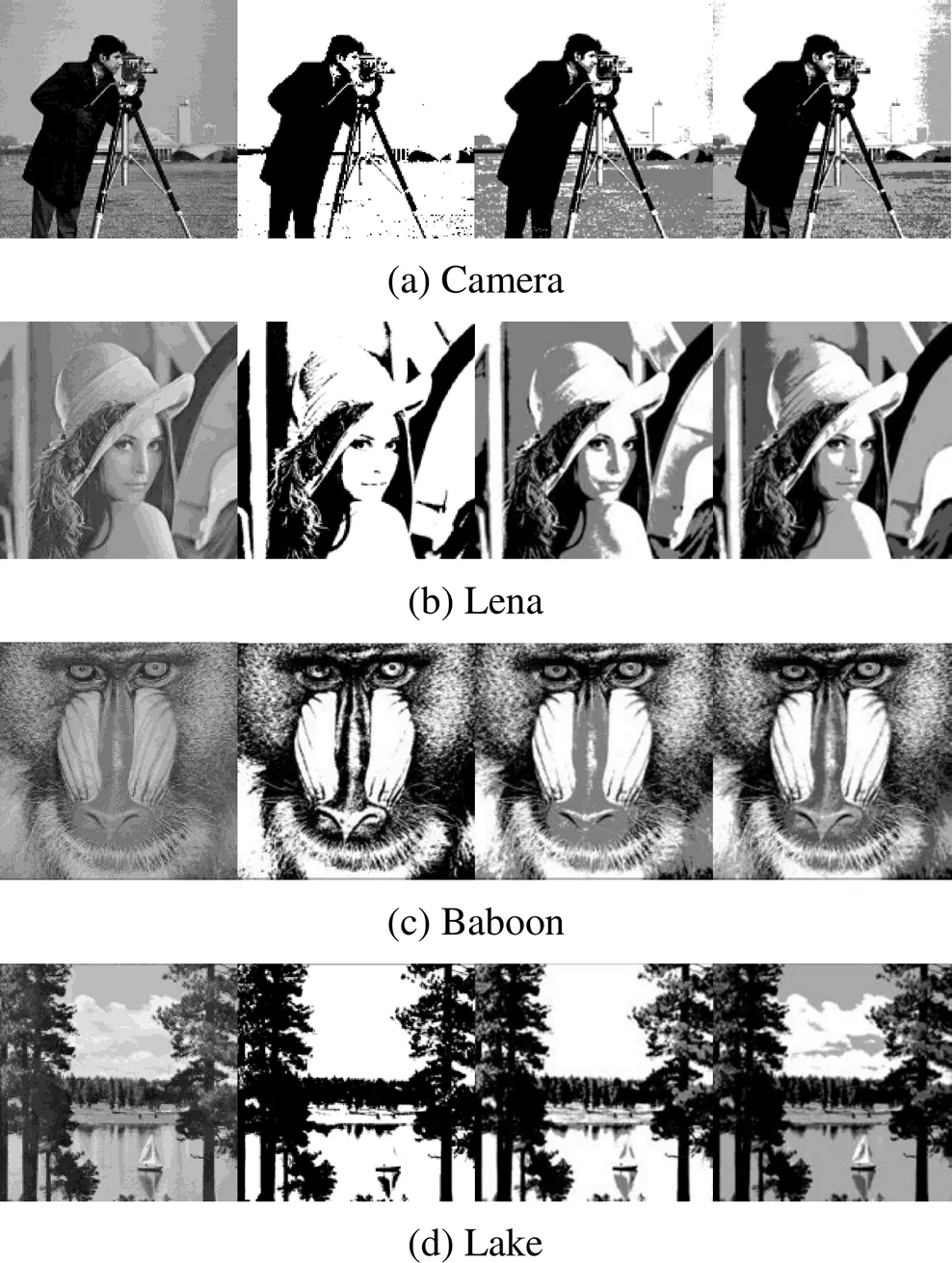
图2 本文算法对各经典图像的分割结果

3.2 穷举算法、粒子群算法、本文算法对比分析

为了验证本文算法的优越性，将上述4幅图像，分别用穷举法、粒子群法和本文算法进行三阈值分割。穷举法采用穷举的搜索模式来寻找函数的最优值。为了使参数对比更加客观，粒子群和风驱动算法的种群数量，最大速度，迭代次数均设置为一致。具体的参数设置：粒子群算法的参数设定如下：种群数量为30，学习因子1＝2＝2，最大速度为3、最大迭代次数为50。风驱动优化算法的参数设定如下：空气粒子数量为30，最大迭代次数为50次，空气粒子速度最大为3，RT的值为3，的值为0.3、的值为0.4，的值为0.4。为了更好地评价本文方法，采用信噪比准则定量分析算法性能。信噪比表达式为：

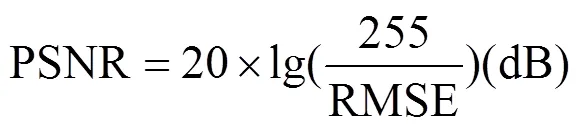
其中均方根误差（root mean square error，RMSE）：

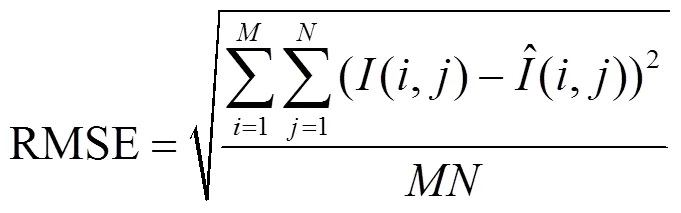
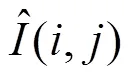
从表1中可以看出，本文算法单阈值分割比穷举法快约10倍，双阈值分割比穷举法快约2000倍，三阈值时比穷举法快约25000倍。总体上，本文算法相对于PSO（particle swarm optimization）相对熵算法快约1.4倍。从PSNR值来看，PSO相对熵算法的PSNR值最低，本文算法的PSNR值大于PSO相对熵算法，最接近于穷举法。可见本文算法的分割效果较好，计算时间更短。风驱动算法与PSO算法的区别是[17]：风驱动算法的速度更新方程中添加了附加条件（如重力和地球自转偏向力），算法更加稳定可靠，具有实际的物理意义，且寻优效率高、收敛速度较快，还可以通过微调系数达到不同的优化拓扑结构。

3.3 Otsu、二维熵法、本文算法对比

为了验证本文算法的优越性，将获得煤岩图像、火焰图像、红外图像作为实验对象，分别用Otsu、二维熵法[13]和本文算法进行单阈值分割。其煤岩图像的分割结果如图3所示，火焰图像的分割结果如图4所示，红外图像的分割结果如图5所示。利用区域内部均匀性测度评价分割的好坏、均匀测度值越高，分割质量越好。3种算法的对比数据如表2所示。

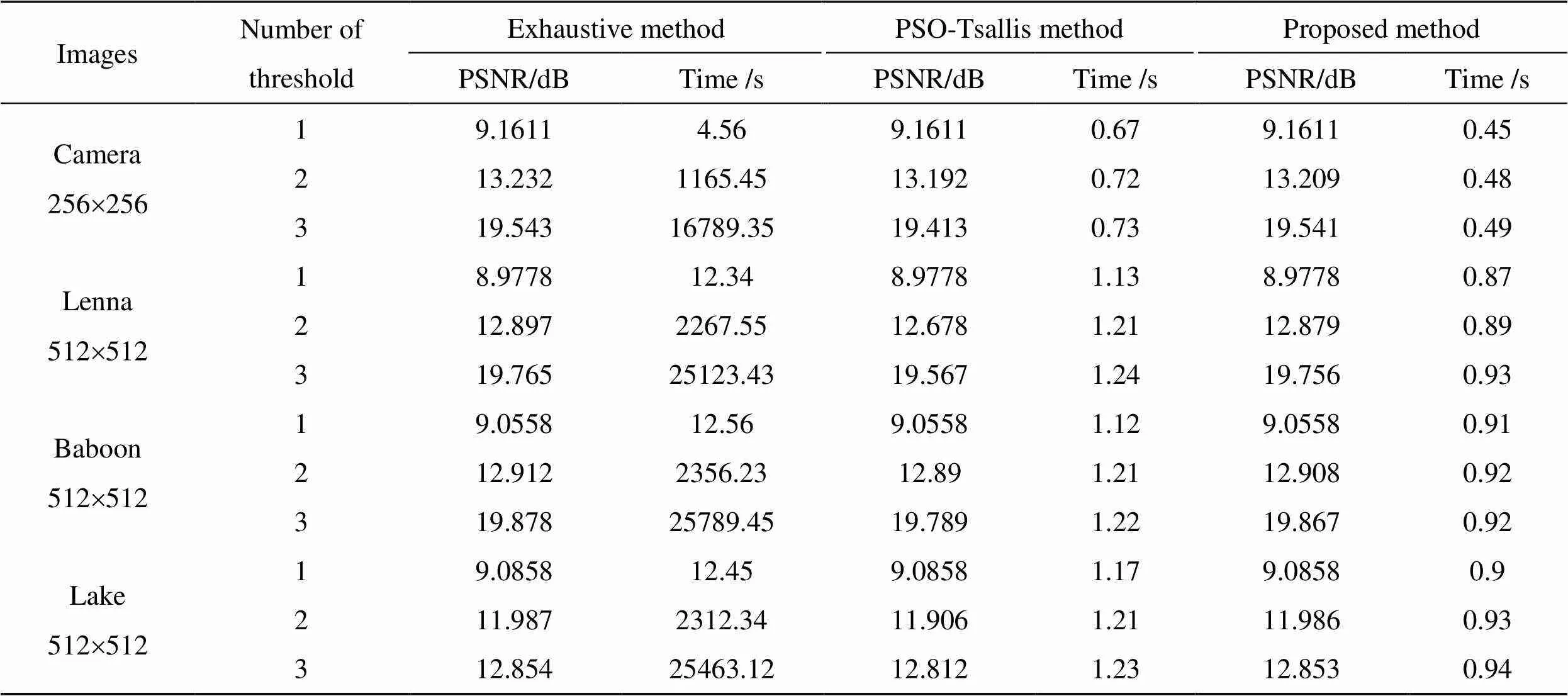
表1 三种方法的PSNR和计算时间对比

图3 煤岩图像的单阈值分割

图4 火焰图像的单阈值分割

图5 红外图像的单阈值分割

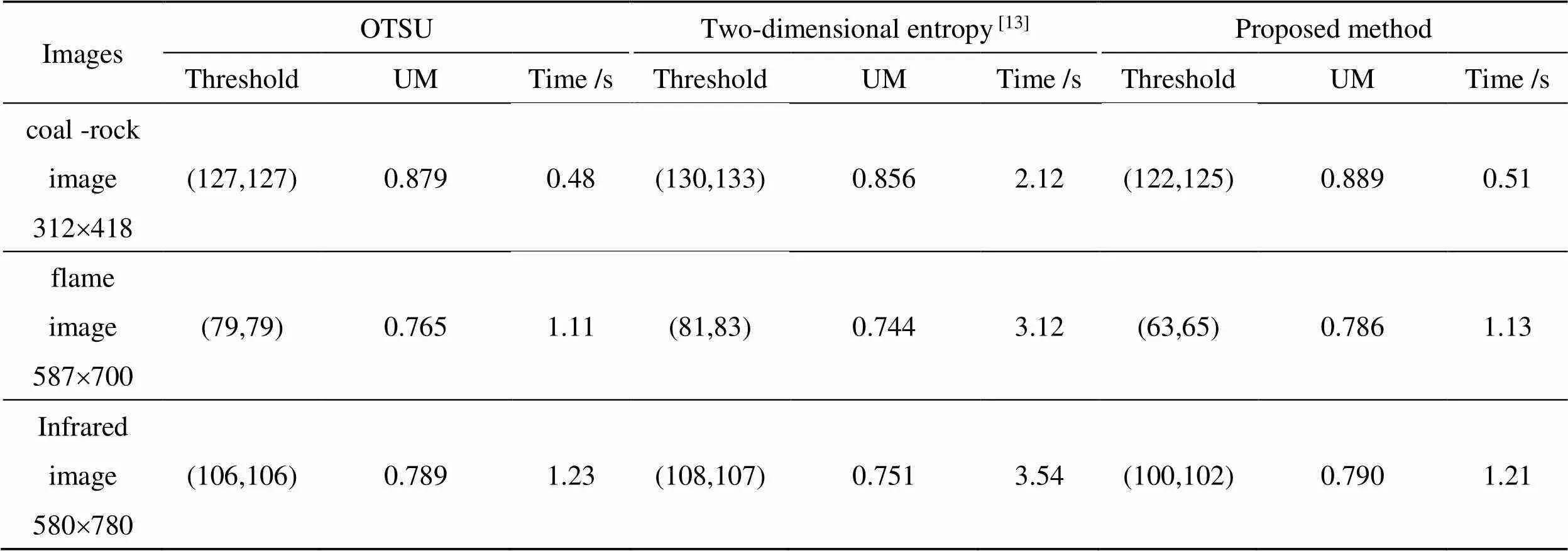
表2 图像单阈值分割数据对比表

分割结果相邻分割区域之间的对比度越大越好，而每一个分割区域内部一致性越高越好，这就是所谓的区域内部均匀性，均匀测度值测量计算如下所示：

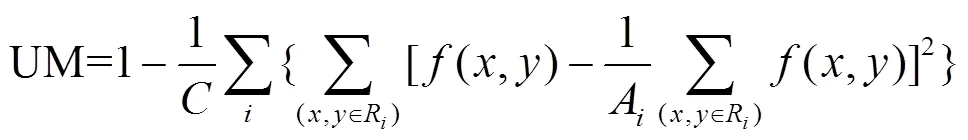
式中：i表示分割区域R的大小（面积）；表示归一化系数。

从图4中，可以明显看到本文算法分割火焰时，分割得到的火焰更加完整，其他两种算法分割效果略逊于本文算法的分割结果。从图5中可以看到，本文算法分割得到的管道更加完整，内部均匀性也较前两种算法更好。从表2中均匀测度值来看，本文算法的均匀测度值均大于OTSU算法和二维熵算法，表明本文的分割算法分割效果较好。在单阈值分割情况下，本文算法的运行时间与OTSU算法的运行时间基本相近，但二维熵法的运行时间比本文算法的运行时间长了4倍左右。可以看出，本文算法在速度上仍然优于二维熵法。由此可以看出，本文算法在分割效果和分割时间上均具有一定的优势。

4 结论

本文提出了一种基于Tsallis相对熵与风驱动优化算法的图像多阈值分割算法。首先将Tsallis相对熵的单阈值分割推广到Tsallis相对熵的多阈值分割，然后将Tsallis相对熵与风驱动优化算法相结合，改善了多阈值分割中、计算量大、计算速度慢的问题。最后将提出的算法与穷举法、粒子群算法进行比较，实验结果表明，基于Tsallis相对熵的多阈值分割，图像分割效果较好、边缘清晰。同时本文算法相比穷举法快了约2500万倍、相比粒子群算法快了约1.4倍。本文算法相对于粒子群算法、收敛速度更快，收敛成功率更高。同时本文算法相对经典的OTSU算法和基于二维熵的多阈值分割算法在分割效果和时间上均具有一定的优势。因此本文提出的算法能够应用于复杂图像的多阈值分割。

[1] 于洋, 孔琳, 虞闯. 自适应粒子群集优化二维OTSU的图像阈值分割算法[J]. 电子测量与仪器学报, 2017, 31(6): 827-832

YU Yang, KONG Lin, YU Chuang. Image threshold segmentation algorithm based on adaptive particle swarm optimization of two dimensional OTSU[J].n, 2017, 31(6): 827-832

[2] 马英辉, 吴一全. 基于二维Renyi交叉熵的刀具磨损图像分割[J]. 电子测量与仪器学报, 2016, 30(12): 1869-1876.

MA Yinghui, WU Yiquan. Image segmentation for tool wear based on 2D Renyi cross entropy[J]., 2016, 30(12): 1869-1876.

[3] 聂方彦, 李建奇, 张平凤, 等. 一种基于Tsallis相对熵的图像分割阈值选取方法[J]. 激光与光电子学进展, 2017, 54(7): 137-144.

NIE Fangyan, LI Jianqi, ZHANG Pingfeng, et al. A threshold selection method for image segmentation based on Tsallis relative entropy[J]., 2017, 54(7): 137-144.

[4] 夏平, 刘小妹, 雷帮军, 等. 基于复小波域树结构化MRF模型的声纳图像分割[J]. 仪器仪表学报, 2016, 37(4): 895-903.

XIA Ping, LIU Xiaomei, LEI Bangjun, et al. Sonar image segmentation based on tree-structured MRF model in complex-wavelet domain[J]., 2016, 37(4): 895-903.

[5] 刘琼, 史诺. 基于Lab和YUV颜色空间的农田图像分割方法[J]. 国外电子测量技术, 2015, 34(4): 39-41,57.

LIU Qiong, SHI Nuo. Farmland image segmentation based on Lab and YUV color spaces[J]., 2015, 34(4): 39-41, 57.

[6] TIAN Y, LI J, YU S, et al. Learning complementary saliency priors for foreground object segmentation in complex scenes[J]., 2015, 111(2): 153-170.

[7] Dirami A, Hammouche K, Diaf M, et al. Fast multilevel thresholding for image segmentation through a multiphase level set method[J]., 2013, 93(1): 139-153.

[8] ZHANG X, XU C, LI M, et al. Sparse and low-rank coupling image segmentation model via nonconvex regularization[J]., 2015, 29(2): 1555004.

[9] Sarkar S, Das S, Chaudhuri S S. A multilevel color image thresholding scheme based on minimum cross entropy and differential evolution[J]., 2015, 54: 27-35.

[10] ZHANG J, LI H, TANG Z, et al. An improved quantum-inspired genetic algorithm for image multilevel thresholding segmentation[J/OL]., 2014: https:// www. hindawi.com/ journals/mpe/2014/295402/fig1/.

[11] LI Y, JIAO L, SHANG R, et al. Dynamic-context cooperative quantum-behaved particle swarm optimization based on multilevel thresholding applied to medical image segmentation[J]., 2015, 294: 408-422.

[12] Ghamisi P, Benediktsson J A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization[J]., 2015, 12(2): 309-313.

[13] 陈恺, 陈芳, 戴敏, 等. 基于萤火虫算法的二维熵多阈值快速图像分割[J]. 光学精密工程, 2014, 22(2): 517-523.

CHEN Kai, CHEN Fang, DAI Min, et al. Fast image segmentation with multilevel threshold of two-dimensional entropy based on firefly algorithm[J]., 2014, 22(2):517-523.

[14] Bhandari A K, Singh V K, Kumar A, et al. Cuckoo search algorithm and wind driven optimization based study of satellite image segmentation for multilevel thresholding using Kapur’s entropy[J]., 2014, 41(7): 3538-3560.

[15] 任作琳, 张儒剑, 田雨波. 风驱动优化算法[J]. 江苏科技大学学报: 自然科学版, 2015, 29(2): 153-158.

REN Zuolin, ZHANG Ruijian, TIAN Yubo. Wind driven optimization algorithm[J].: Natural Science Edition, 2015, 29(2): 153-158.

[16] 田栋, 曹中清, 陈彬彬, 等. 基于目标跟踪的风驱动优化粒子滤波算法研究[J].微电子学与计算机, 2017(5): 30-34.

TIAN Dong, CAO Zhongqing, CHEN Binbin, et al. Research on wind driven optimization particle filter algorithm based on target tracking[J]., 2017(5): 30-34.

[17] 张天能. 基于风驱动算法及小波神经网络的有限元模型修正研究[D]. 北京: 北京交通大学, 2018.

ZHANG TianNeng. Finite Element Model Updating Based on Wind Driven Optimization and Wavelet Neural Network[D]. Beijing: Beijing Jiaotong University, 2018.

Fast Image Segmentation with Multilevel Threshold Based on Tsallis Relative Entropy and Wind-Driven Optimization Algorithm

LI Fenhong1，LU Jing1，ZHANG Zhiguang2

(1.,,726000,;2.,,100124,)

This paper proposes a fast image-segmentation algorithm with a multilevel threshold based on the Tsallis relative entropy and wind-driven optimization algorithm. First, the principle of the Tsallis relative entropy is analyzed, and single threshold segmentation is extended to multilevel threshold segmentation. Then, a Gauss distribution is used to fit the image histogram information after segmentation, and the Tsallis relative entropy is used to determine the best segmentation threshold. To improve the speed of the threshold-segmentation algorithm, a wind-driven optimization algorithm is used to find the optimal solution of the Tsallis relative-entropy function. Finally, the proposed algorithm is compared with exhaustive and particle swarm optimization algorithms.The proposed algorithm is also compared with the Otsu algorithm and the multi threshold-segmentation method based on two-dimensional entropy. The experimental results show that the proposed algorithm can be used for multi-threshold segmentation of images with high speed and high accuracy.

image segmentation, Tsallis relative entropy, Gaussian distribution, wind driven optimization, particle swarm optimization

A

1001-8891(2020)10-0994-07

2018-11-07；

2020-09-15.

李粉红（1978-），女，陕西商州人，硕士，副教授，研究方向：应用数学、智能算法及应用、数据分析与处理，E-mail：lifenhong8327@126.com。

陕西省科技厅项目（2020JM-630）；陕西省教育厅项目（17JK0240）；陕西省社科界重大理论与现实问题研究（2018Z168）。