某引水工程面板堆石坝稳定及应力变形分析

何晓萌，孙向东，訾 娟，刘芙荣

（中水北方勘测设计研究有限责任公司，天津 300222）

代古寺供水方案拟在白龙江代古寺修建水源水库取水，穿西秦岭长隧洞分别至武山分水口、张家川分水口、庄浪分水口、华亭分水口、崆峒分水口、镇原分水口，到达输水总干线工程末端庆阳分水口。供水方案包括水源工程、输水总干线工程和调蓄水池工程。其中，水源工程为代古寺水源水库，总库容3.18亿m3，拟采用混凝土面板堆石坝，最大坝高143 m；输水总干线长422.23 km。代古寺面板堆石坝地震工况计算取抗震设防烈度为Ⅷ度，设计基本地震加速度值为0.15 g。

1 计算方法

1.1 邓肯-张E-B模型

静力计算中，坝体堆石的静力本构关系采用邓肯-张双曲线E-B模型［1，2］，其切线弹性模量可表达为：

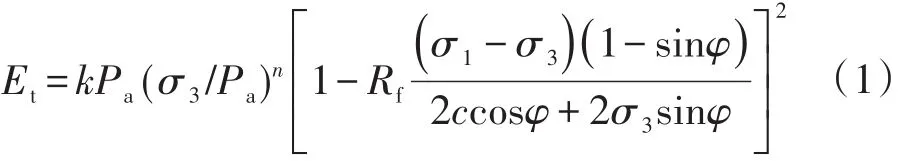
式中：Et为切线弹性模量（kPa）；c为材料凝聚力（kPa）；φ为材料的内摩擦角（°）；k为切线弹性模量基数，由初始切线弹性模量Ei与侧限压强σ3试验曲线确定；n为切线弹性模量指数，由初始切线弹性模量Ei与侧限压强σ3试验曲线确定；Pa为单位大气压力（kPa）；Rf为破坏比；σ1-σ3为偏应力（kPa）。

卸载时切线弹性模量Eur随着侧限压强σ3变化而变化，可用下式计算：

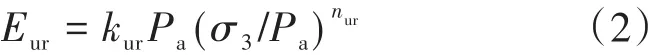
式中：Eur为切线弹性模量（kPa）；kur、nur是由试验确定的2个系数，其确定方法与k、n相似；其余变量含义同上。

设加载状态函数为：

历史上最大的SS值表示为SSm，按现有σ3计算最大应力水平Sc：

然后，将Sc与土体当前应力水平S比较来判别切线弹性模量Et'的取值。当S≥Sc，判别为加荷，取Et'=Et；当 S≤0.75Sc，判别为卸荷，取 Et'=Eur；当 0.75Sc≤S≤Sc时，则在Et和Eur之间内插。

切线体积模量为：

式中：kb为体积模量系数；m为体积模量指数；其余变量含义同上。

模型同时还考虑粗粒料内摩擦角φ随侧限压强σ3的变化：

式中：φ0为σ3等于单位大气压力时的φ值（°）；Δφ为反映φ值随σ3而降低的参数（°）；其余变量含义同上。

2 稳定分析

如果坝坡由于自重及外荷载（如施工期加载、蓄水、地震等）产生的剪应力大于土体的抗剪强度，就会发生坝坡破坏。本工程用基于刚体极限平衡理论的简化的毕肖普（Bishop）法进行计算。它是建立在土体刚体极限平衡假定基础上的条分法，假设潜在的滑动面为圆弧，并将滑动面上的土体划分成若干土条，视土条为刚体，根据平衡条件计算土条在滑面上的滑动力和阻滑力。再根据滑面上土体整体的力矩平衡条件确定土体沿滑面的滑动稳定安全系数。与简单条分法相比，简化的Bishop法最重要的改进是考虑土条间的水平向作用力。为了确定土条的内力和沿滑面的滑动稳定安全系数，它还假设：①土条满足竖向力平衡，条间剪切力为零；②滑面上各点的安全系数均相同。

3 计算模型及参数

3.1 计算模型

下坝址混凝土面板堆石坝坝体及地基有限元计算单元如图1所示。静力计算中，堆石坝的静力本构关系采用邓肯-张双曲线E-B模型。由于面板与垫层2种材料性质相差较大，在特定的受力条件下有可能在其接触处会产生错动滑移或脱空。根据《混凝土面板堆石坝设计规范》（SL228-2013），在应力和变形有限元分析中，应反映坝体与混凝土面板接触面及面板接缝的力学特性。在模拟施工填筑和蓄水过程中，将面板与垫层之间的接触关系采用一个虚拟的接触面进行模拟。稳定计算中，堆石料采用非线性摩尔库伦抗剪强度指标。

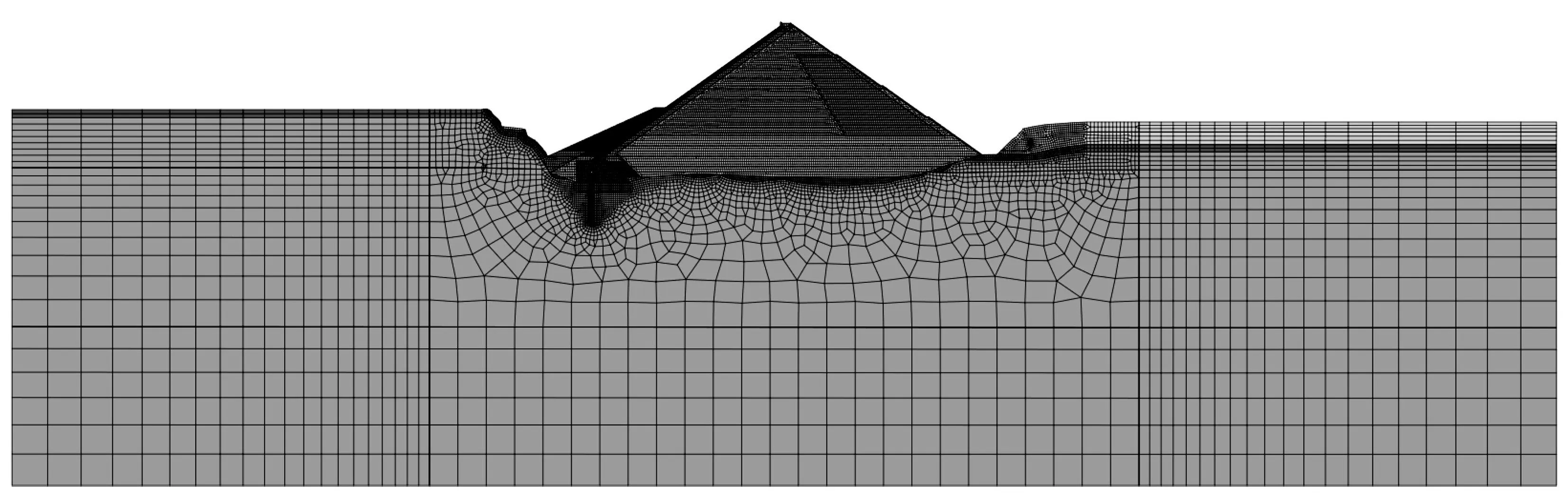
图1 MIDAS二维计算坝体及地基有限元单元

MIDAS二维计算选取具有代表性的堆石坝断面建立有限元模型，模型分为混凝土面板、过渡区、主堆石区、下游堆石区、垫层区、碎石盖重区、壤土铺盖区、趾墙、防渗帷幕、覆盖土、弱风化区及基岩，并赋予不同的材料参数。坝基底部采用全约束状态，上下游采用法向约束。

3.2 计算参数

坝体各材料参数取值详见表1，其中混凝土面板参考工程经验取C30混凝土。坝体及坝基渗透参数参考工程经验取值，详见表2。面板与垫层接触力学参数，详见表3。

表1 代古寺面板坝筑坝材料计算参数

表2 坝体及坝基计算渗透参数取值

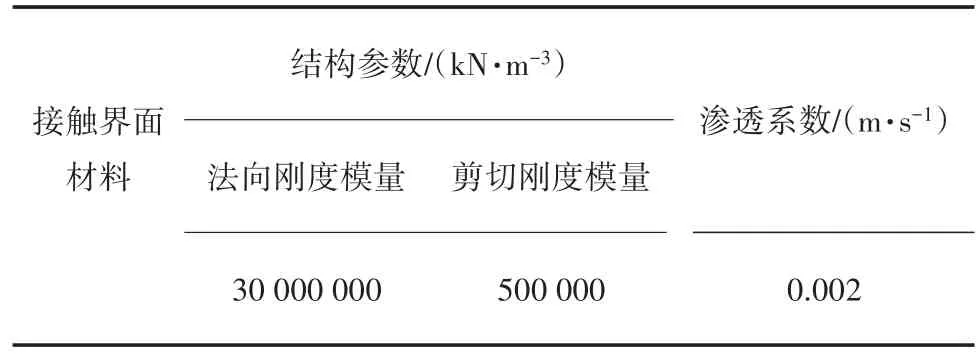
表3 面板与垫层接触力学参数

4 计算内容及成果分析

4.1 渗流计算分析

经计算，正常蓄水位工况下坝体、地基单宽渗流量为0.19 L/s，坝体最大渗透坡降下游溢出点、防渗帷幕分别为0.02、1.23。堆石坝在正常蓄水位1 804 m时渗流总水头云图如图2所示，堆石坝在正常蓄水位1 804 m时渗流后压力水头云图如图3所示。

图2 堆石坝在正常蓄水位1 804 m时渗流总水头云图

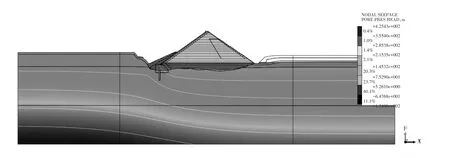
图3 堆石坝在正常蓄水位1 804 m时渗流后压力水头云图

4.2 位移及应力计算成果

（1）坝体堆石区完建工况和正常蓄水位工况下顺河向上游、顺河向下游和竖向最大位移计算结果详见表4，混凝土面板正常蓄水位（运行期）工况下最大挠度值及对应高程计算结果详见表5。

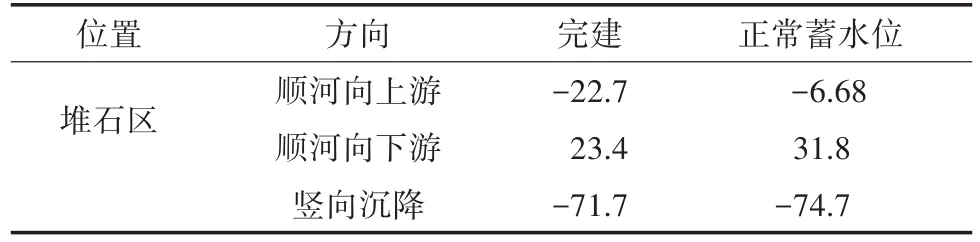
表4 E-B模型计算各工况坝体堆石区典型位置最大位移cm

表5 E-B模型计算正常蓄水位工况下混凝土面板最大挠度值及对应高程

（2）坝体堆石区在各计算工况下的小主应力、大主应力、顺河向正应力、铅垂向正应力计算结果详见表6，混凝土面板在正常蓄水位工况下第1主应力、第3主应力、沿面板向正应力、垂直面板向正应力计算结果详见表7。

表6 E-B模型计算各工况坝体典型位置应力kPa

4.3 坝坡稳定分析计算成果

在抗滑稳定计算中，应用GeoStudio中SLOPE/W模块基于刚体极限平衡理论的简化的毕肖普法，计算边坡最小安全系数，结果详见表8。

表8 坝坡抗滑稳定安全系数计算结果

计算结果与规范规定的最小安全系数进行比较，确定坝坡的安全稳定。本工程等级为1级。各工况下相应上、下游坝坡最危险滑动面如图4所示。

图4 各工况下相应上、下游坝坡最危险滑动面

5 结论

（1）坝体、坝基的渗流量在正常范围内，对该水库的运行影响不大。

（2）坝体堆石区应力计算结果在规范允许的范围内，满足规范要求。面板拉应力最大值超出C30混凝土允许最大拉应力，可以通过加配顺坡向钢筋解决该问题。

（3）应用基于刚体极限平衡理论的简化的毕肖普（Bishop）法，计算正常运行条件和非常运行条件下坝坡抗滑稳定安全系数，得到各工况最小安全系数均大于规范对应规定的最小安全系数，坝坡稳定。