基于概率约束的稀疏统计套利模型研究——以中国市场为例

徐凤敏，李雪鹏

(西安交通大学 经济与金融学院，陕西 西安 710061)

一、引 言

统计套利策略作为一种数量化的投资手段在20世纪80年代达到鼎盛，目前广泛应用于对冲基金和投行主营业务中。在成熟市场经济体中，统计套利策略年收益在15%至20%，在中国等新兴市场有极大的收益潜力。统计套利根据资产的历史价格信息构建不依赖经济含义的数理模型以发现具有长期均衡趋势的两类资产，并利用短期的价格偏离构建空头和多头投资组合，最终在均值回复的假设下当价格回复到均衡的时候反向对冲。与无风险套利策略相比，统计套利存在价差序列的发散风险，但增加了套利机会，且应用对象范围更大，操作手段更灵活。常见的类型有配对交易、多因子模型、指数追踪、增强型指数[1-6]。配对交易是应用最早、最成熟的统计套利策略，Avellaneda和Lee认为配对交易是统计套利的起源，因此统计套利在应用中也被称为配对交易[7]。配对交易是一类市场中性套利策略，包括形成期和交易期。在形成期内需要确定可用于交易的资产对象(股票、期权期货、外汇及债券)，符合交易条件的两个资产在价格上应该有长期一致趋势；在交易期内配对交易者应该确定价格偏离时触发交易的条件，及具体的交易策略。Avellaneda和Lee扩展了配对交易的内涵，提出了更一般的多元配对交易(Generalized Pairs Trading，GPT)，即研究两个投资组合间的配对交易[7]。Perlin为某确定资产寻找配对的投资组合，该问题被称为拟多元配对交易(Quasi-Multivariate Version of Pairs Trading，QMVPT)[8]。

国外学者关于配对交易的研究开展较早，主要集中于配对交易理论方法的设计。Krauss按照建模方法将统计套利中的配对交易策略分为五类：距离法、协整法、时间序列法、随机控制法和其他法[9]。

Gatev等最早给出价差平方和测度(Sum of Euclidean Squared Distance，SSD)用以描述资产价格的一致性趋势，并给出了配对交易策略的两步框架，这里称为距离法(Distance Method，DM)[10]。Pole选择价差收益率的方差取代SSD，Chen等使用股票收益率的皮尔逊相关系数代替SSD，实验表明可以取得超过一般DM方法一倍的收益[2，11]。Vidyamurthy最早使用协整方法研究两个资产的配对交易问题，在APT模型成立假设下给出了协整套利一般框架[1]。该框架分为三步，第一步在于选择具有相关关系的配对资产；第二步是对价差进行交易性测试，和距离法类似；最后使用非参数信号判断是否发生交易。Elliott等用时间序列方法在状态空间中为价差建模，将两个资产的价差视为均值回归的高斯马尔可夫链和一个高斯噪声，引入首达时间理论建立了配对交易分析框架，并得到交易时间和开仓、平仓信号[12]。Do等采用收益率序列差的错误定价，和上文的框架类似建立了配对交易框架，不同在于由于引入了APT模型，使得收益序列差的刻画变得复杂[13]。Jurek和Yang应用随机控制理论研究配对交易问题，假设配对组合的价差满足Ornstein-Uhlenbeck过程，利用资产价格的动态变化，考虑预算约束和资本约束得到Hamilton-Jacobi-Bellman(HJB)方程，并推出最优投资策略和价值函数的闭式表达解[14]。

自2010年3月推出融资融券业务以来，国内关于配对交易的研究逐渐增多，主要关注配对交易策略在中国市场的应用。王春峰等利用DM方法设计了基于价格差异的配对交易策略，利用沪深300成份股2006—2009年的数据研究了两只股票间的配对交易问题，结论显示策略月收益均值在1%[15]。仇中群等利用协整模型研究了股指期货的跨期套利问题，利用沪深 300股指期货模拟数据检验了有效性[16]。张波等引入了股指期货跨期套利的EGARCH-M模型并提出期货合约间的修正协整关系，结果显示优于传统的GARCH套利模型[17]。胡伦超等结合协整和DM方法构建了两阶段的配对套利策略，基于上证50的实证显示该策略在不同费率下均可以获得超额收益[18]。

从以上文献可以发现：第一，距离法和协整方法都需要在形成期内确定满足一致趋势的配对组合。其中距离法使用相关测度检验相似性，协整法需要配对资产满足协整关系，并在交易期内采用非参数方法确定交易信号。而时间序列方法和随机控制方法都忽略了形成期内配对组合的确定，假设已经找到了具有一致性趋势的股票，主要研究集中在交易期内如何确定最优的交易信号和交易策略。第二，国内外研究两资产配对交易较多，如股票、期货合约间，对多元配对交易和拟多元配对交易研究相对较少。

传统配对交易只涉及两个资产，在形成期内确定配对组合是容易的，协整方法和距离法在多项式时间内都可以找到满足要求的配对组合。当考虑GPT或QMVPT问题时，由于维数爆炸问题，原有的方法不再适用。GPT或者QMVPT的模型刻画是困难的，预期收益的不确定性变化同样使得约束和目标难以表达。为此将资产的收益视为服从某一分布的随机变量，通过概率约束刻画收益的不确定性[5]。此外从成本角度出发，需要限制配对交易组合的资产数量，通过加入稀疏约束限制配对组合的规模。

综上所述，本文聚焦于统计套利中配对组合的确定，拟建立带有概率约束的稀疏优化模型研究GPT和QMVPT问题。对于QMVPT问题，考虑中国市场的卖空限制、配对组合规模，研究重点在于给定某一资产时，在形成期内寻找与其配对的投资组合，包括组合内资产的选择和权重的确定；对于GPT问题，允许资产卖空，且考虑配对组合规模，重点研究如何最优地确定满足配对交易条件的两个套利投资组合。

二、模型提出及理论分析

配对交易意图寻找长期内收益或者价格具有一致变动趋势的资产，并利用资产间的瞬时偏离获取套利收益。资产间的一致趋势对于风险的抵御至关重要，是套利机会最终收敛的必要条件，而交易期内资产组合间的偏离程度和出现频率决定了套利收益的大小。本文从这两个目标出发建立概率优化套利模型，并加入控制组合规模的稀疏约束，目的是寻找在长期来看具有一致变动趋势，但短期内出现偏离的资产配对组合。在后续分析中，考虑两种情景下的配对交易：标的指数和投资组合的拟配对交易问题，以及投资组合间的多元配对交易问题[7-8]。需要明确的是，本文的模型并不局限于对指数的套利问题，而是可以广泛应用于单一或者同类型资产的套利组合构建，从而为套利投资者提供一种主动寻求套利机会的解决方案。

(一)定义和符号说明

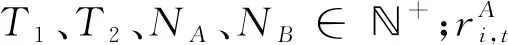
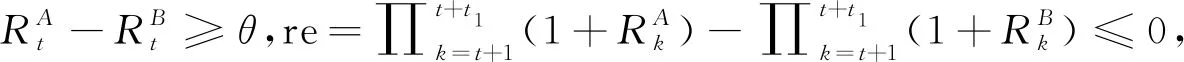
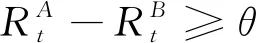
(二)拟多元稀疏统计套利模型及分析

假设套利组合A为已知的标的指数(NA=1，ωA=1)，下面构建一个这样的套利组合B，即和指数在一定持有期内具有长期稳定趋势，但在交易期内某一时刻指数和套利组合资产收益率序列相较于正常水平具有更大的偏离幅度。考虑到未来收益的不确定性，套利机会是否出现并不是一个确定事件，因此在约束中考虑套利条件的不确定约束。此外套利组合的规模不宜过大或出现不可操作的小权重，因此需要稀疏约束对投资组合规模加以限制。综上所述，提出拟多元稀疏统计套利模型(Quasi-Multivariate Sparse Statistical Arbitrage Model)，以下记为QM-SSAM模型，如式(1)：

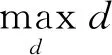
s.t.P{rA-(rB)TωB≥d}≥1-ε，d>0，

eTωB=1，L≤ωB≤U，‖ωB‖0≤K

(1)

式(1)中ε∈[0，1]是预设参数，随着ε的减少，指数能以更高概率达到预期偏离[5]。QM-SSAM模型是带有单概率约束的双目标稀疏优化模型，求解该模型可以得到指数的最优套利组合，其中第一层目标保证了指数和套利组合B有一致的变动趋势，即指数和套利组合B具有均值回复特征，称为追踪目标；第二层目标使得指数和套利组合B在套利期内收益偏差尽可能大，称为波动目标，这使得定义中描述的有效套利机会更可能出现，进一步增加了套利的收益能力。稀疏约束保证了套利组合至多只包含K个资产；单概率约束刻画了指数正向套利机会出现的不确定性，即只对指数进行卖空操作。资金预算约束保证了资本全部用于投资，L和U表示买入阈值的上下界。

(三)多元稀疏统计套利模型及分析

对于多元配对交易而言，假设组合A和B内包含多个资产且都可以使用融资融券操作，此时可以考虑正向和反向两类有效套利机会。类比于QM-SSAM模型，加入稀疏约束，买入阈值约束以及资金预算约束，提出多元稀疏统计套利模型(Multivariate Sparse Statistical Arbitrage Model)，以下记为M-SSAM模型，如式(2)：

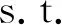
‖ωA‖0+‖ωB‖0=K1，

U1≤ωA≤L1，U2≤ωB≤L2

(2)

M-SSAM是带有双概率约束的双目标稀疏优化模型，用于最优的确定配对组合A和B。ε1∈[0，1]、ε2∈[0，1]都是预设参数；需要满足1-ε1+1-ε2≤1⟺ε1+ε2≥1，并且当d1=d2时等号成立。组合A和B在交易期内卖空操作的难度相仿，出于减少卖空操作难度而只关注正向套利机会减少了交易期内的套利机会，故使用双概率约束刻画A和B两类套利机会。当d1≥0且d2≥0，即式(2)中的两个概率约束都成立，套利者可以在交易期内关注正向或者反向套利机会。对于式(2)，当RA只包含一种资产，且给定ωA=1时，式(1)是(2)只包含第一类套利的特殊形式；当RA=RB，即A和B来自同一个资产池中，令ω=ωA-ωB，可以将式(2)等价写为关于变量ω的单变量模型，其中ωA对应解的正部，-ωB对应解的负部；当RA和RB互斥时，给定ω1=(ωA；ωB)，可以将式(2)改写为关于ω1的单变量模型。

双目标使得模型求解变得困难，在后文转化和算法设计中，引入风险权重因子δ，δ1∈[0，]将模型转化为多目标的线性加权和形式，即以及改写后的单目标约束稀疏随机优化模型涉包含稀疏约束和概率约束，这使得该问题是NP-hard，不存在解决这类问题的多项式时间算法。在下节中假设预期收益率可以由多因子模型表示，利用因子的分布信息给出该问题的近似模型和一般求解算法。

三、问题的转化和求解

带有概率约束的稀疏优化问题是NP-hard问题，本节利用因子的矩信息，结合分布式鲁棒的方法将不确定性约束转化为确定性约束，从而将模型(1)和(2)转化为约束稀疏优化问题，然后利用量子粒子群算法的思想，设计了一类新的混合算法。

(一)概率约束转化

考虑概率约束P{c(ω，ξ)≤0}≥1-α，其中ω为未知量，ξ是参数随机向量，一般处理思想是将其转化为确定性等价形式或者逼近形式。但实际中，我们并不能确定收益率的具体分布，因此确定性转化是困难的。通过有限的样本数据观察，可以计算样本均值、方差，当数据量足够大的时候可以近似总体的均值、方差。在无法获得变量ξ全部分布信息时，Xu等利用分布集合刻画其不确定性，使用分布式鲁棒方法，借助ξ的一阶和二阶矩信息以及无限对偶理论，将概率约束转化为一系列的锥约束或者半定约束[5]。按照这种方法给出概率约束的近似逼近。

假设每个资产的收益率都是由k个市场因子(随机变量)决定(如单因子CAPM模型、三因子Fama-French模型)，则有：

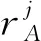
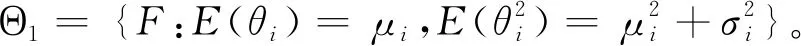
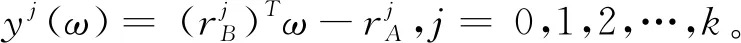
s.t.eTωB=1，L≤ωB≤U，‖ωB‖0=K，d≥0，

(αi+ηi-ξi，si+βi，si-βi)∈L3，i=1，2，…，k，

(αj+η1j-ξ1j+φyj(ωB)，Sj+βj，Sj-βj)

∈L3，j=1，2，…，k，

λ，φ∈；α，β，ξ，η，ξ1，η1，s，S∈k；ξ，η，ξ1，

η1，s，S≥0；φ≥0，β<0

(3)

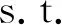
0≤ωA≤L1，0≤ωB≤L2，

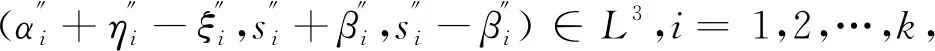
∈L3，j=1，2，…，k，

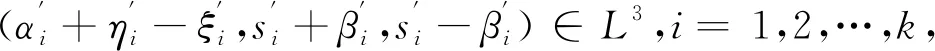
∈L3，j=1，2，…，k，

λ″∈；

φ″≥0，β″<0，

λ′∈；

φ′≥0，β′<0

(4)

(二)算法设计

QM-SSAM和M-SSAM的安全近似模型(3)、(4)是一类带有稀疏约束的二次锥规划问题。本文根据近似模型的特殊形式设计一类新的量子粒子群算法(Quantum-Behaved Particle Swarm Optimization，QPSO)，并将其应用于约束稀疏优化问题的求解。对于单变量稀疏约束和上下界约束，引入0-1整数变量y∈{0，1}n对其进行等价转化，如式(5)所示，其中⊙表示分量相乘。故上节得到的近似模型等价于一类0-1混合整数规划问题。

‖ω‖0=K，ω∈n

L≤ω≤U⟺eTy=K，y∈{0，1}n

L⊙y≤ω≤U⊙y

(5)

量子粒子群算法最初用于连续变量的模型求解，每一次的迭代结果都带有小数部分。国内的学者已经成功将量子粒子群算法应用于整数和混合整数规划的求解，研究主要结合新的迭代公式和整数截断方法提出修正算法[19-21]。近似模型两个变量具有特殊结构，当y确定后，模型(3)和(4)是二次锥规划问题。鉴于凸规划问题的求解有许多成熟的优化算法，求解难度大大降低。由此本文提出一种基于两步法确定模型解的混合量子粒子群算法，在每次迭代中使用量子粒子群算法求解0-1变量y(选择最大的K个分量)，将其代入近似模型求解降维后的子问题得到ω并将近似模型中的最优目标值作为y的评价指标，即子问题目标函数越小，则对应y值评价越高。

混合量子粒子群算法过程如下：

1.输入

模型参数及数据，QPSO算法粒子数m，最大迭代次数Max，迭代误差ν；

2.初始

2.1 令k=0，初始化规模为m的粒子群X={X1，X2，…Xm}，第i个粒子为

Xi(k)=[Xi，1(k)，Xi，2(k)，…，Xi，n(k)]，Xi，1(0)～U(0，1)，对X做后续方案1或2操作。

2.2 更新个体和全局最佳位置

Pi(k)=[Pi，1(k)，Pi，2(k)，…，Pi，n(k)]，G(k)=Pg(k)，g∈{1，2，…，m}；

更新收缩扩张系数，ρ=1-k/(2×Max)

由以下过程，计算f(X(k))=f(P(k))=[f(X1(k))，f(X2(k))，…，f(Xm(k))]；

3.QPSO算法迭代

3.1 调用QPSO算法

pi，j(k)=φj(k)·Pi，j(k)+[1-φj(k)]·

Gj(k)，φj(k)～U(0，1)

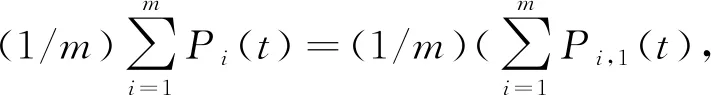
Xi，j(k+1)=pi，j(k)±ρ·|Cj(k)-Xi，j(k)|·

ln(1/ui，j(k))，uij(k)～U(0，1)；

3.2 更新k=k+1；

3.3 按照模型不同使用后续方案1或方案2，对X(k)进行指标选择；

4.子问题求解

4.1 提取X(k)的非零指标lX，使用CVX工具箱求解原问题降维后的m个子问题；将子问题的目标函数值记为f(X(k))=[f(X1(k))，f(X2(k))，…，f(Xm(k))]；

4.2 则对任意i∈{1，2，…，m}，更新个体最优位置，

令g=argmin1≤i≤m{f(Pi(k))}，更新全局最优位置，

5.终止条件

当迭代次数k≤Max且|f(G(k))-f(G(k-1))|≥ν，返回步3，否则转步6；

6.输出

粒子群全局最优位置G(k)，非零指标lX，子问题最优解和最优值。

粒子群X每次更新后对应一个实数矩阵，需要从每个粒子中提取K个位置，对应选择进入配对组合的资产。由此在3.3提出针对模型(3)下的方案1，具体而言：对于粒子群X，从每个粒子n个维度中选择最大的K个，将其数值令为正数aq，其余位置为0。对含有双变量的模型(4)，当RA≠RB时引入ω∈RNA+NB可以将其改写为单变量形式，方案1仍然适用。

当RA=RB时，考虑到A和B的互异性，需要明确A和B各自包含资产的类别。因此，提出方案2：对于粒子群X，随机选择Ka∈{1，2，…，K}，从每个粒子n个维度中最大的Ka个令为正数bq，最小的K-Ka令为负数cq。此时lX包含两部分，正负指标集分别指代组合A和B所包含资产。

四、实证分析

基于国内股票市场真实数据，应用提出的混合量子粒子群算法，检验QM-SSAM中主要参数对套利组合的影响；针对不同的交易场景，对指数的拟配对交易了实证检验，并根据不同的时间窗口验证每种情境下的套利收益。对于M-SSAM模型，利用行业信息提供的天然的分组，研究同行业内以及行业间的统计套利问题。

(一)数据集及参数

本文数据来自于国泰安金融数据库，包括2012年1月4日至2020年3月26日，基于流通市值计算的Fama-French三因子数据，以及上证50指数(000016)，深证100指数(399330)，沪深300指数(000300)，中证500(000905)指数及成份股的日收盘价格数据，下文称为data1-data4，其中每个数据集包含2000条记录。

Gatev应用DM方法，将套利时期的价差序列的标准差视为开仓信号，并在价差恢复到零时平仓[10]。本文同样采用非参数估计思路，由形成期内计算的标准差，即买入投资组合的收益小于卖空投资组合收益的整数倍标准差时开仓买入；当有效套利条件满足时，套利者进行平仓。为了保证套利条件的收敛，在统计套利收益机会时，只在交易期的前一半时间允许触发套利机会，后面时间作为套利收敛的缓冲期。令单次套利的收敛时间为5天。 在混合粒子群算法中，令量子粒子群数量为10(data1，data2)或者50(data3，data4)，最大迭代次数100，迭代误差为1.0e-6，aq=bq=0.01，cq=-0.01。实验中默认参数设置，令稀疏度为20，资产下界[0，0，…，0]T，资产的上界为[0.5，0.5，…，0.5]T，显著性ε为0.05，形成期和交易期长度分别为60天和40天。

(二)风险因子分析

考虑单因子(k=1)的CAPM模型和三因子(k=3)的Fama-French模型，将模型(2)的两种转换形式记为QM-SSAM-CAPM (QSC)，以及QM-SSAM-FF3(QSF)。以60天为时间窗，对data1-data4进行滚动实验，其中每个数据集上计算32次。

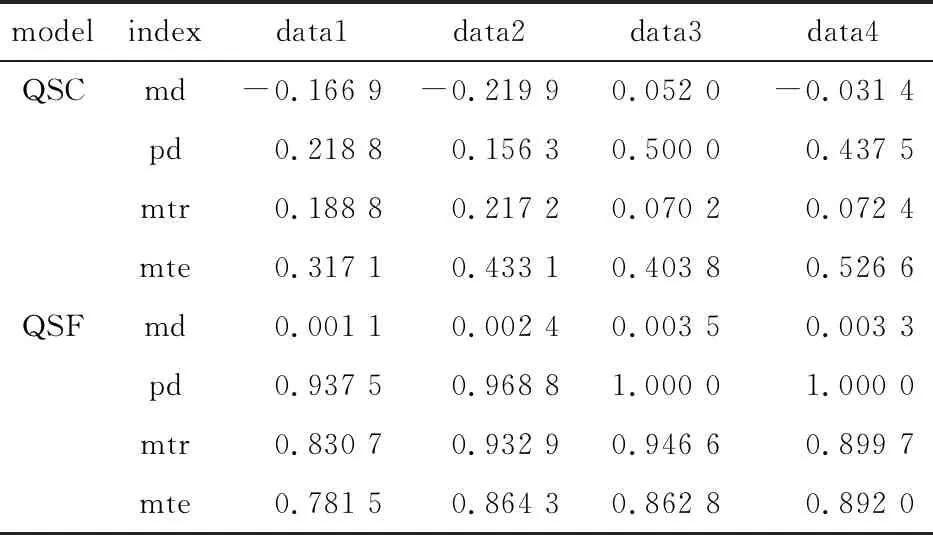
表1 data1-data4下QSC和QSF比较

表1给出了两类不同模型在不同指数下波动目标的平均值(md)，以及波动目标为正数的概率(pd)，可以发现QSF模型以超过90%的概率获得正的波动目标，即满足我们要求的套利条件，并且在上证、深证以及中证三个指数上都获得了超过QSC模型的正的波动值。此外形成期和套利期的平均相关系数(mtr，mte)也都显然大于QSC模型，意味着QSC模型求得的套利组合预期的均值回归行为很可能不会在交易期内出现，加剧了配对交易的发散风险。QSF模型形成期相关系数较高，这给套利者足够的信心认为模型发现的组合和指数的相关关系在套利期仍然会延续，而套利期的最小系数为0.781 5也恰好印证这点。因此后续的分析中默认使用QSF模型。同样地，将模型(4)的两种转换形式记为M-SSAM-CAPM(MSC)，以及M-SSAM-FF3(MSF)，下文中默认使用MSF模型求解。

QSF模型一项重要参数为风险因子δ，图1至图3给出了对波动目标，以及不同参数下套利组合和指数间的相关性变化，每条曲线上的数据点均由data1～data4滚动实验的平均值给出。

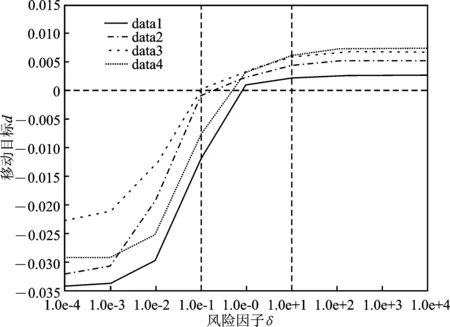
图1 风险因子对波动的影响图

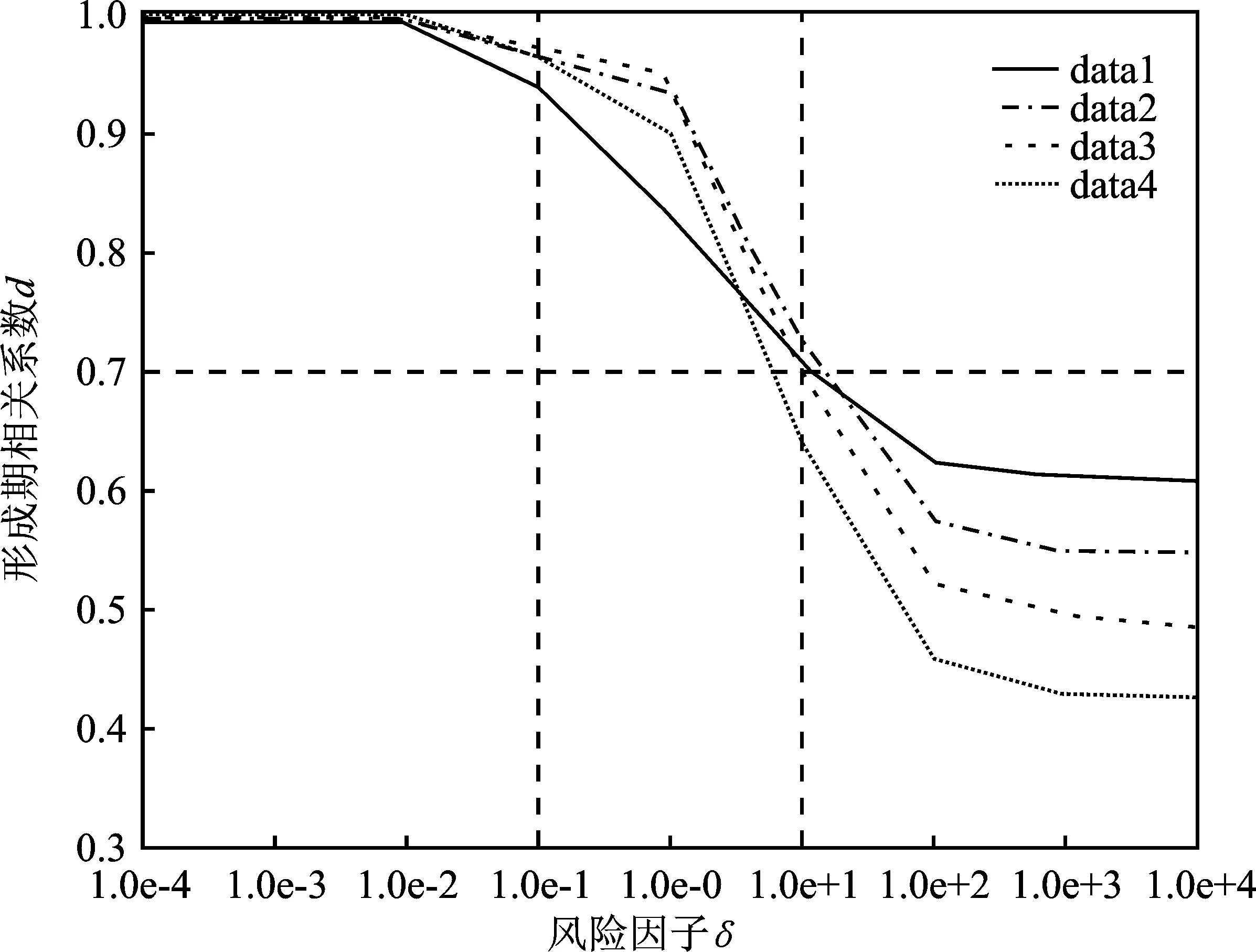
图2 风险因子对形成期相关系数的影响图

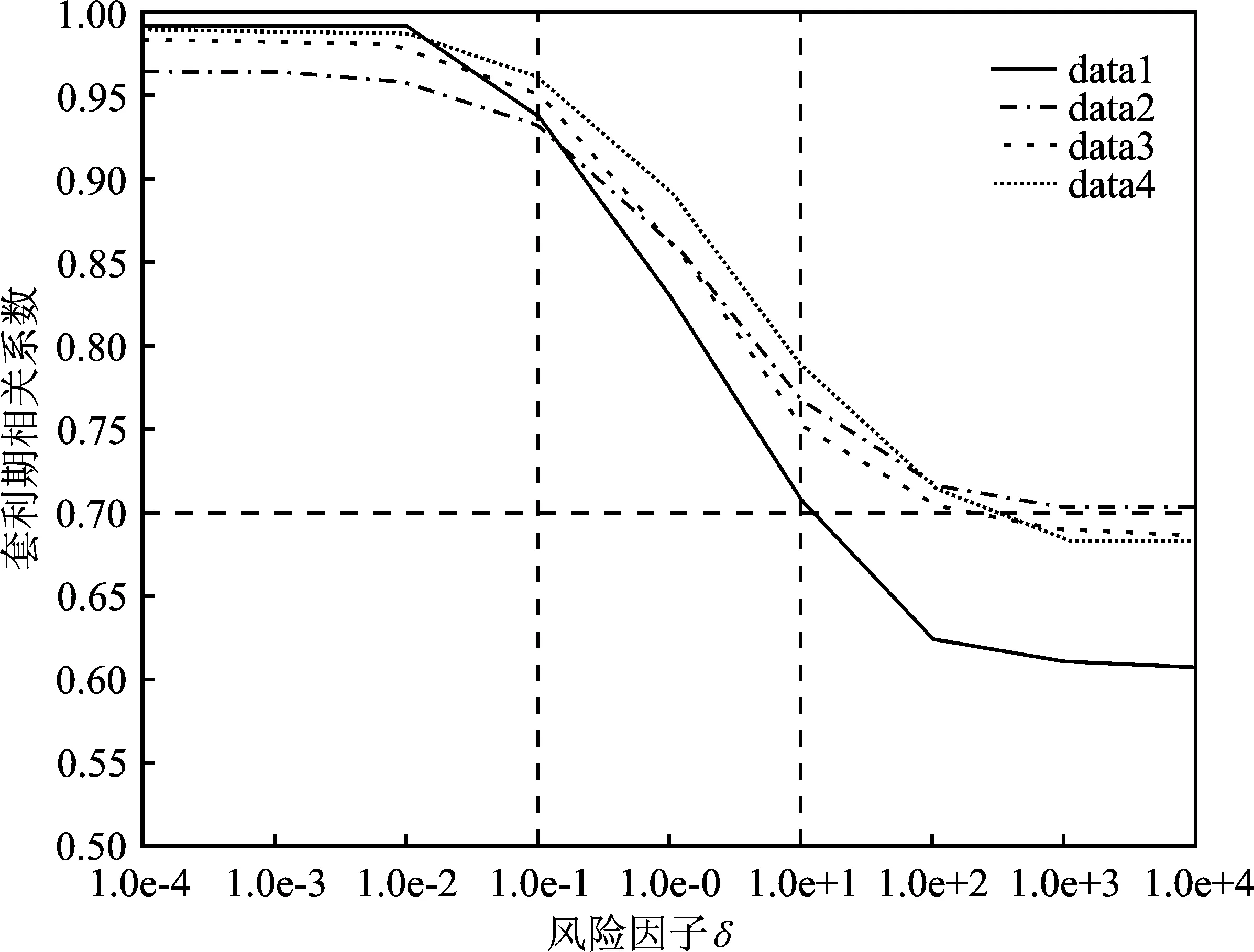
图3 风险因子对套利期相关系数的影响图

从套利的角度出发，令波动目标d>0，形成期和套利期内组合和指数的相关系数均在0.7以上，得到了风险因子的合适区间为[1.0e-1，1.0e+1]。

(三)稀疏资产配置

通过应用上证50指数的数据(data1，2014/7/21-2014/12/16)研究不同稀疏度下拟配对交易的资产选择。

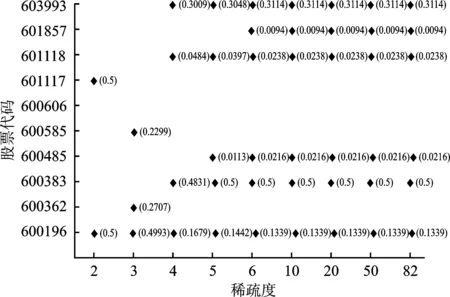
图4 稀疏资产选择图

图4中稀疏度最小取2，最大取82(样本内去除停牌及ST股票)。为了简化图表，选择权重大于0.05%的资产，共计10只股票，纵坐标给出了不同稀疏度下的资产选择及对应权重。可以发现在稀疏度小于6时，资产的选择呈现波动特征，说明稀疏约束对资产选择影响较大。图5描述了追踪目标、波动目标及加权目标随着稀疏度的变化，结合图5的结果，当稀疏度大于10以后，资产组合的构成趋于稳定，这也为证明模型及混合量子粒子群算法的有效性提供了实证解释。

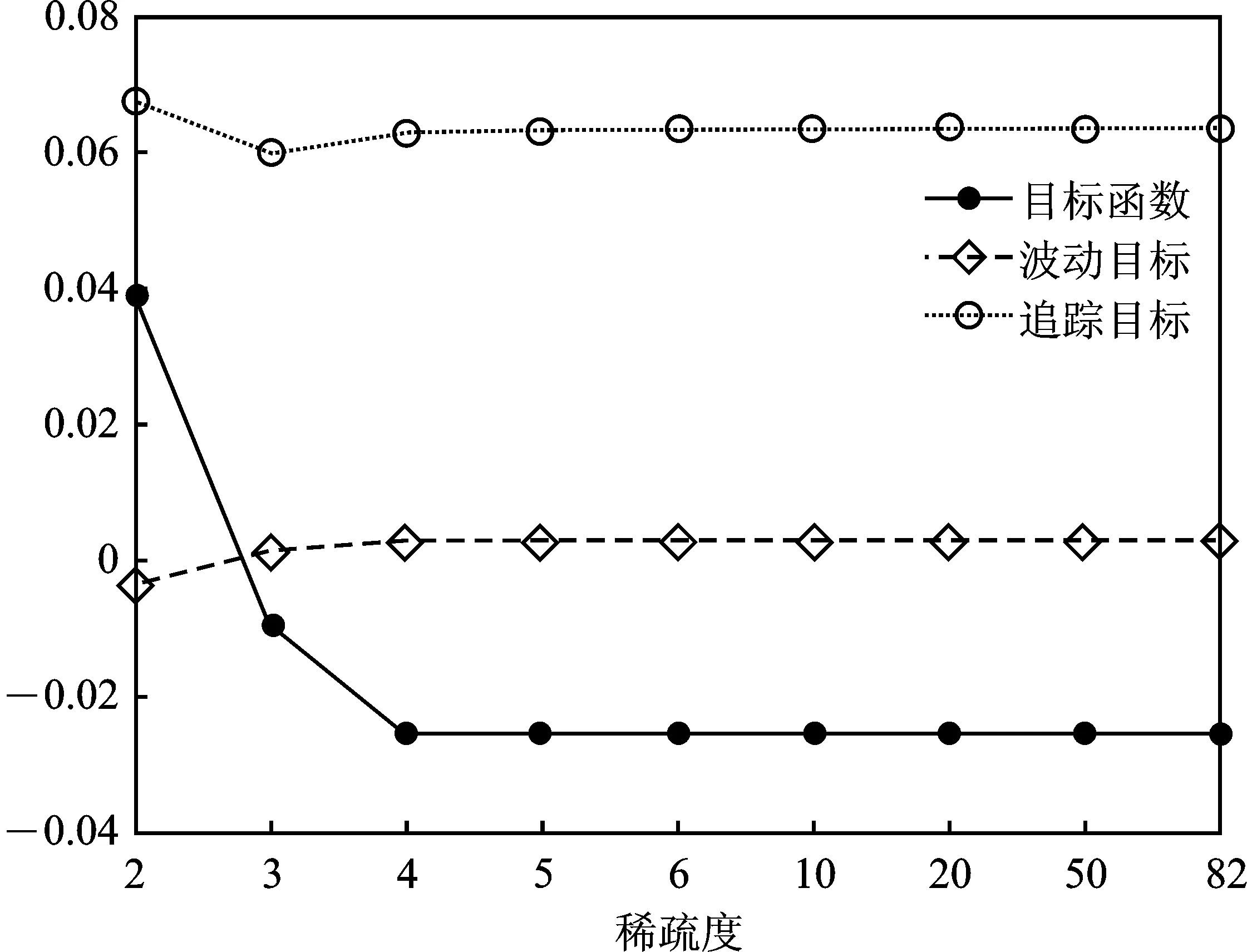
图5 稀疏度对目标函数的影响图

(四)拟多元配对交易收益

通过研究拟多元配对交易的套利收益，给定五个特殊的套利时段，即上升区间(up-up，2014/7/21-2014/12/16)，上升下降区间(up-down，2015/3/11-2015/8/3)，下降区间(down-down，2018/4/17-2018/9/7)，下降上升区间(down-up，2015/11/1-2016/4/11)，及市场震荡区间(oscillation，2019/7/8-2019/12/3)。

表2给出了不同数据集下模型的年化净收益(nt)和套利的成功率(sr)，其中nt由re复利计算得到，sr为套利成功次数和开仓次数的比率。可以发现QSF模型在多种市场情形下均获得了正的套利收益，其中对于up-up和up-down的情况，均以概率1的条件获得了正的收益；对于另外三种情形，最后的套利净收益为正，但在套利期存在套利失败的行为，其中最高的失败可能性为20%。

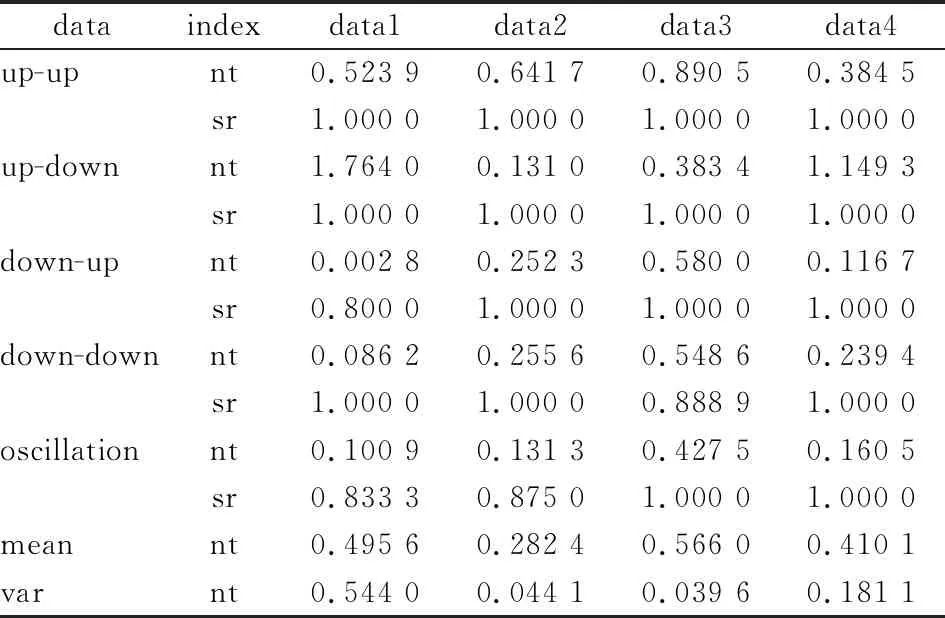
表2 特殊时段下的套利收益比较

通过比较不同市场指数套利收益的均值和方差，可以发现深证100和沪深300的套利收益较为稳定，而上证50和中证500的套利收益波动较大。沪深300指数的套利收益较高，深证100的收益区间较小。

(五)多元配对交易收益

将data3(2014/1/1-2015/5/14)中的股票按照中证行业分类标准分为十类，其中能源股26只、原材料股49只、工业股90只、可选消费股59只、主要消费股29只、医药卫生股33只、金融地产股72只，信息技术股45只、电信业务股5只，公用事业股22只，分别记为行业1到行业10。本节研究同行业以及不同行业间的多元配对交易。令Data3前240天为形成期，顺序的40天为交易期，其中行业内套利行为，稀疏度设定为行业内股票数量；行业间配对交易，稀疏度设定为20；其他参数统一设置为ε1=ε2=0.6，δ1=1.0e+1。

表3中“-”表示没有获得正收益，套利失败。可以发现总体的套利成功率达到86%；行业内的配对交易，即RA=RB，均获得了正的年化收益；值得注意的是，行业7-金融地产出现失败的概率最高，且出现损失的数额巨大，这和金融行业容易受到市场冲击有着密切关系；信息行业和实业相对稳健，行业1、3、5、9只出现了一次失败的情形，行业8、10在该数据下全部成功。

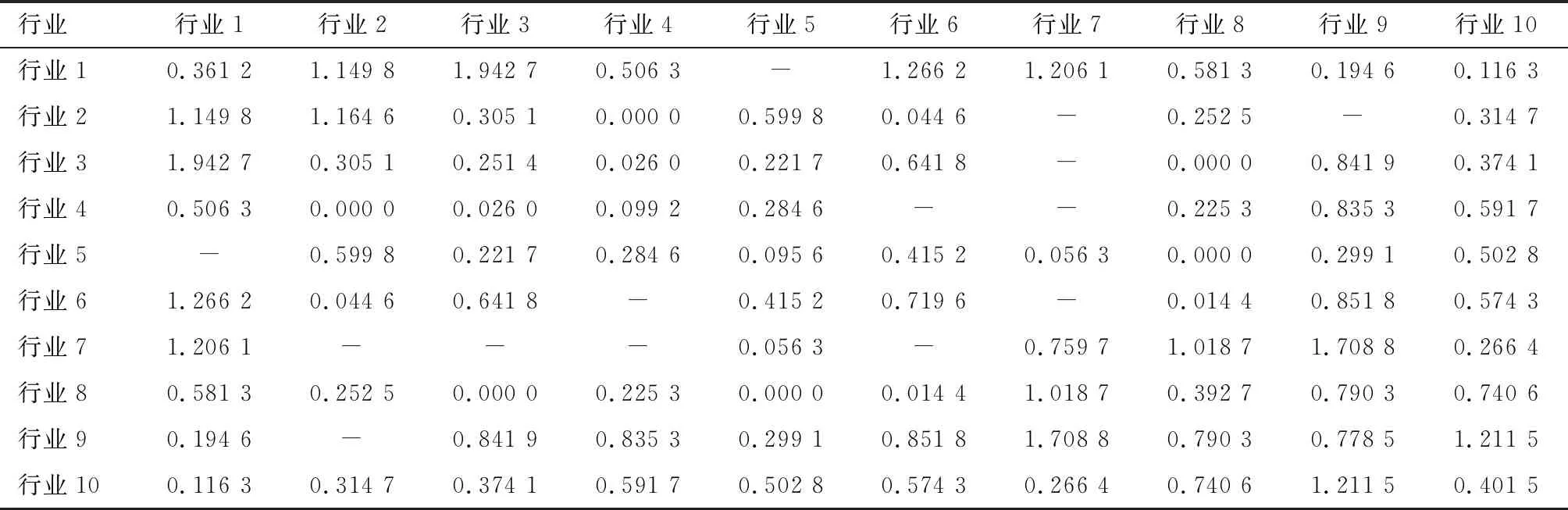
表3 行业间多元配对交易年化收益统计

五、结 语

传统配对交易主要研究两资产套利关系，建模中主要应用距离法、协整法和时间序列法等，并使用参数或者非参数估计方法确定开平仓及止损信号。本文聚焦于多资产的配对交易问题，利用稀疏优化的思想，引入概率约束刻画预期收益偏离的不确定性，建立了两个带有概率约束的稀疏优化模型。值得注意的是，在QM-SSAM模型中，考虑到中国市场卖空限制加入单概率约束，只关注对指数的卖空操作，增强了实际应用性。对于M-SSAM模型，由于资产组合事先完全未知，考虑融券卖空机制加入双概率约束研究两类套利机会更加贴近实际。

文中建立的QM-SSAM和M-SSAM模型是一类NP-hard问题。本文借助Xu提到的分布式鲁棒方法，在预期收益可以由因子表达的前提下，利用因子的一阶矩和二阶矩信息近似初始概率模型。针对转化后的约束稀疏优化问题，根据量子粒子群理论构建了一类混合量子粒子群算法，其中每一步子问题等于求解一个凸规划问题。

实证部分应用上证50，深证100，沪深300，中证500指数及成份股在2012年1月到2020年3月的历史数据对模型及算法进行了检验。可以发现因子集合包含信息越多，对最后的结果越有利，文中给出拟配对交易的一组算例说明了在同样情况下，使用三因子的近似模型会在交易期出现更多的套利机会。在敏感性分析中，拟多元配对交易模型对风险因子较为敏感，随着δ增加，目标中预期偏离d显著增大，由此带来了更多套利可能，但也会加剧收益差的发散风险，结果表明合理区间应该在[1.0e-1，1.0e+1]。资产的稀疏配置说明了所提出的模型及算法可以获得稳定的稀疏套利组合。为了具体展示模型的泛化能力和适用性，给定了五种复杂的市场环境，指数的拟多元配对交易模型在data1到data4的结果表明可以获得正的套利收益。综合四种指数，可以发现沪深300的收益性最高，风险相对较低。最后，利用沪深300的指数及成分研究了行业间的多元配对交易问题，结果表明在多数行业间可以获得正的套利收益。

综上所述，本文提出的统计套利模型能够自适应地从资产池中选择有限数目的股票用于构造配对组合，并确定组合权重，对金融机构和个人投资者都有着重要的应用价值。在以后的研究中将尝试运用动态规划的思想，建立多阶段的配对交易模型，引入交易费用等约束，使得模型更接近真实市场。