基于分箱策略的巨灾债券风险息差定价模型

陈惠民，孟生旺，吕秀萍

(1.中国人民大学 统计学院，北京 100872；2.河北经贸大学 金融学院，河北 石家庄 050061)

一、引 言

随着经济发展和气候变化，自然灾害造成的经济损失越来越严重。譬如，2008年的汶川地震造成了1 480亿美元的经济损失。传统的保险手段很难为如此高额的巨灾损失提供完全保障，因此一种很自然的想法便是通过证券化的手段将这些巨灾风险转移到资本市场。巨灾风险证券化的主要方式是巨灾债券，就是利用资本市场来解决保险市场承保能力有限的金融创新工具，保险公司(再保险公司)将巨灾风险可能导致的或有支付转换为确定性支付，从而将自己无力承担的巨灾风险转移到资本市场。

关于巨灾债券定价方法的研究主要有三种思路，第一种思路是采用风险中性定价法，针对巨灾债券的或有支付进行定价；第二种思路是运用均衡模型进行定价，即首先选定各个市场参与者的效用函数，然后基于市场总体效用最大化来求解均衡条件下的巨灾债券价格；第三种思路是进行回归分析，即利用巨灾债券的发行数据或者二级市场的交易数据，选取合适的定价因子和函数形式，对巨灾债券的风险息差构建回归模型。前两种思路是从金融经济理论出发，定价模型需要很多假设条件与较为复杂的数学推导，第三种定价思路寻找影响巨灾债券风险息差的主要因素，并建立相应的定价模型，从实际应用的角度看，操作性较强，也具有较好的解释性。由于现有文献在实证研究中使用的数据量较小，而且定价因子的选择也存在一定争议，所以本文主要讨论实证研究方面的问题，并提供相应的解决方法。

模型形式、定价因子以及样本数据为回归分析中值得重点关注的三个环节。在实证研究中，现有文献大多采用普通线性回归模型，线性模型有严格的假设，无法刻画复杂的非线性关系。因此，许多文献研究风险息差和定价因子的非线性关系，构建拟合效果和预测能力更优的回归模型。而定价因子的研究相对较为分散，大多文献只针对感兴趣的变量进行分析，容易产生遗漏重要变量的问题。此外，实证需要的样本数据收集也有一定难度，巨灾债券缺乏公开的市场，需要从多个金融机构整理获得。

不少学者对线性模型进行了拓展，采用对数线性模型和Wang变换模型。譬如，Major等基于179个一级市场的巨灾债券数据，揭示了巨灾债券的风险息差与期望损失之间的对数线性关系[1]；Papachristou基于192个一级市场的巨灾债券数据，采用广义加性模型，描述了风险息差与期望损失之间的对数关系[2]；Galeotti等基于176个巨灾债券的数据对各种模型进行了比较研究，结果发现，在考虑金融危机的情况下，线性模型、对数线性模型与Wang变换模型的效果比较接近，但在不考虑金融危机的情况下，线性模型能够得到相对较好的预测效果[3]。广义加性模型引入了连接函数和平滑函数，非常适合刻画变量间非线性关系，但是其经济解释能力较弱，较难向投资者进行介绍。Henckaerts等进一步提出了基于数据驱动的分箱技术，并将其应用于广义加性模型，从而使得最终的模型兼具灵活性和解释性[4]。本文尝试借鉴Henckaerts等提出的方法，将其运用于巨灾债券风险息差的定价。

在实证研究中，定价因子的选择至关重要。定价因子大致上可以分为两类，一类是关于巨灾债券的微观信息，包括期望损失、触发类型、发行规模、债券期限等；另一类是关于金融市场和自然环境的宏观信息，包括金融市场环境、再保险市场环境、是否发生巨灾事件等。在现有文献中，关于定价因子的选择存在较大差异，譬如Lane等在定价模型中首次使用了再保险价格指数[5]；Cummins等使用的定价因子包括S&P500股价指数、BBB级债券指数和BBB级公司债的信用价差[6]；Braun使用的定价因子包括再保险价格指数和BB级公司债的信用价差[7]；Gürtler等使用的定价因子包括再保险价格指数、公司债的信用价差和S&P500价格指数[8]；而Stupfler等基于S&P500价格指数计算了条件在险值(CVaR)，并将其引入定价模型[9]。期望损失是大部分定价模型都会采用的定价因子，而其他定价因子的选择则各不相同，暂时还没有文献进行全面的梳理。

数据匮乏是进行实证研究较大的障碍，在公开数据库中，只能获取巨灾债券在一级市场的发行数据，没有任何二级市场的交易数据。这导致大部分研究只能针对巨灾债券的一级市场，只有少量文献研究了二级市场。在现有文献中，使用的数据规模都比较小，譬如Lane最早应用回归模型研究了巨灾债券的风险息差，但研究样本仅选取了1997年到1999年发行的巨灾债券数据[10]。基于小样本的回归模型可能出现相互矛盾之处，例如Gürtle等的研究结果表明，巨灾债券的触发机制对风险息差没有影响[8]；而Cummins等和Dieckmann发现，实际损失触发机制会提高巨灾债券的风险息差[6，11]。

本文在现有文献的基础上，主要完成了下述工作：一是在建立广义加性模型的基础上，考虑因变量的不同分布假设，应用进化树对连续变量进行分箱处理，最终构建广义线性模型，从而使得定价结果兼具精确性和解释性；二是全面考虑历史文献提及的定价因子，并首次引入了新的Logit风险度量值，通过各种评价指标和十折交叉验证，选取了最优的定价因子组合，使得最终的定价模型更加稳健；三是收集了Lane和Artemis两家公司提供的巨灾债券一级市场数据，通过整理和交叉验证，得到643条从1999年至2018年发行的巨灾债券数据，比现有文献中的样本量增加了50%以上，为定价模型的稳定性提供了可靠保证。

二、定价因子

巨灾债券的息票率可以分解为两部分，分别是无风险收益率和风险息差，可以用公式表示为c=r+ρ，其中r表示无风险收益率，ρ表示风险息差。无风险收益率一般使用银行隔夜拆借利率或国债利率，其数值大小可以直接在市场上询价获得，所以在巨灾债券的定价中通常关注的是关于风险息差的定价。

在风险息差的定价模型中，通常将风险息差分解为不同的定价因子。譬如，Fama等最早提出的风险息差定价模型为ρ=β0+β1X1+…+βnXn，其中α为截距项，表示巨灾债券的超额收益率；X1，X2，…，Xn为定价因子，表示巨灾债券蕴含的不同风险源和不确定因素[12]。定价因子可以归为两大类：一类主要是与巨债债券直接相关的指标，提供巨债债券的具体信息；另一类主要是与宏观环境相关的指标，提供外部环境信息，间接影响巨灾债券的风险息差。

(一)微观定价因子

为方便起见，我们将保险公司承担的原始巨灾损失进行标准化处理，即将其表示为保险金额的比例，标准化处理公式如下：

(1)

其中，t表示起赔点，即当原始巨灾损失(Loss)超过t以后，保险公司开始赔偿；h表示全损点，即保险公司承担的最大损失为h-t。经过标准化处理以后，保险公司承担的巨灾损失Z将在[0，1]区间取值，其分布函数为F(z)，生存函数为S(z)=1-F(z)。相应地，起赔概率可以表示为PFL=Pr(Loss>t)=Pr(Z>0)，全损概率可以表示为PLL=Pr(Loss>h)=Pr(Z=1)。

影响巨灾债券风险息差的微观定价因子包括期望损失、风险附加、债券评级、债券期限、触发机制、风险源和发行日期等。

期望损失(EL)是巨灾债券定价的核心指标，其数学表达为EL=E(Loss)=E(Z)。历史文献表明，期望损失是目前学界公认最为有效的定价因子。巨灾债券的期望损失主要由第三方风险评估机构建立的巨灾模型提供。国际上主流的巨灾模型来自三家公司，分别为AIR，EQECAT和RMS。出于商业上的考量，第三方风险评估机构通常对其巨灾模型进行了加密，因此很难对期望损失的合理性和科学性进行判断。譬如，Gürtler等发现，在发生巨灾之后，期望损失的回归系数会显著提高，这可能预示着巨灾模型输出的期望损失缺乏稳健性。虽然第三方巨灾模型提供的期望损失可能存在偏误，但本文仍然在定价模型中保留了该变量，并同时引入新的定价因子对其进行修正[8]。

Lane最早将起赔概率(PFL)和全损概率(PLL)同时引入了定价模型[10]。但由于期望损失、起赔概率和全损概率存在较强的相关性，同时引进模型会导致较为严重的共线性问题，因此在后期的定价模型中，都仅将期望损失作为定价因子。

由于巨灾损失具有明显的厚尾特点，期望损失不能完全度量巨灾损失的变异性，因此本文将引入其他风险度量值重点衡量巨灾损失的尾部特征。基于Wang变换的风险度量值是较为常见的风险度量指标，Wang变换的数学表达为g(t)=Φ(Φ-1(t)+Φ-1(α))，其中Φ(t)为标准正态分布的分布函数，Φ-1(α)为标准正态分布的分位数函数，α∈[0，1]表示给定的分位数水平，SZ(z)表示分布的生存函数[13]。基于Wang变换的风险度量值的数学表达为：

(2)

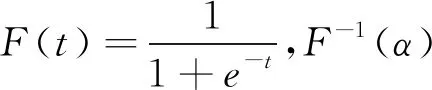
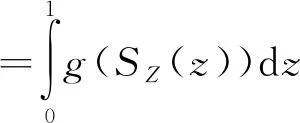
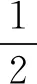
F(F-1(PLL)+F-1(α))]

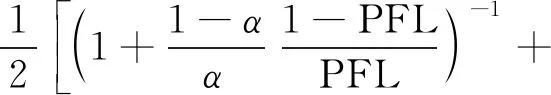
(3)

通过将Logit分布作为扭曲函数的分布，则获得具有显示表达的风险度量值，该风险度量值衡量了损失分布的整体状况。本文将风险附加(Load)定义为Logit风险度量值与期望损失之差，用以度量损失分布的尾部特征，其数学表达为Load=LGT-EL。

债券评级对巨灾债券的价格具有重要影响，国际上主流的三家债券评级机构分别为Moody’s、S&P和Fitch，其中绝大部分巨灾债券的评级由S&P提供。通常情况下，债券的评级越高，说明其违约风险越低，因此债券的收益率会较低。本文将S&P的债券评级结果数值化，用1到14分别表示B-等级到AAA等级的债券，用0表示评级缺失的债券，并将该定价因子命名为Rating。

不同评级的巨灾债券，其价格乘数也不尽相同，价格乘数是风险息差与期望损失之比，评级较差的债券，其价格乘数较高，从而会导致风险息差上升。现有文献通常采用BB等级公司债的信用价差来描述巨灾债券的信用水平。本文对该指标进行改进，对于评级缺失的巨灾债券，采用巨灾债券发行时BB等级公司债的信用价差，而对于其他不同等级的巨灾债券，则采用发行日期对应等级公司债的信用价差，数据来自ICE Benchmark Administration。本文将该定价因子命名为Cspread。

巨灾债券的期限也是重要的定价因子，当债券期限较长时，债券的不确定性增加，投资者会要求较高的收益率。用Term表示巨灾债券的期限。

债券发行机构的声誉和经验也可能会影响巨灾债券的收益率，譬如Braun的研究结果表明，瑞士再保险公司拥有良好的风控能力和声誉，其发起的巨债债券更受欢迎，因此投资者要求的风险息差和收益率会相对较低[7]。用Cedenttimes和SPVtimes两个变量分别来衡量保险公司和SPV在巨灾债券市场上的经验，其中Cedenttimes表示保险公司发起巨灾债券的次数，SPVtimes表示SPV发行巨灾债券的次数。一般而言，保险公司和SPV发起的巨灾债券越多，其发行经验就越丰富，也就越有可能被市场认可和接受，其发行巨债债券的风险息差也会越低。

巨灾债券的触发机制也是目前文献中考虑较多的定价因子。触发机制是指巨灾损失达到一定程度从而触发损失赔付的条件和流程。巨灾损失可以是实际损失(Indemnity)、行业损失(Industry loss)、模型损失(Modelled loss)、参数损失(Para)、参数指数损失(Para index)或混合损失(Multiple)，其中实际损失触发机制是指保险公司根据保障区域内的实际损失来确定损失是否达到触发条件并进行赔付，对保险公司最为有利，基差风险最小。但是，由于实际损失的评估过程耗时较长且不够透明，容易导致道德风险，所以与其他触发机制相比，投资者通常会要求较高的风险息差。

巨灾债券保障的风险源主要包括三种类型，即飓风(Wind)、地震(EQ、)和其他(Other type)风险源，它们对巨灾债券的风险息差存在不同程度的影响。巨灾债券保障的风险区域通常划分为五个类别，即美国(US)、欧洲(EU)、日本(JP)、多区域(Multi region)和其他地区(Other region)。此外，部分文献也会将风险源为美国和多区域定义为高风险地区(Peak)，从而将巨灾债券划分为高风险区域债券和非高风险区域债券。考虑到不同的风险源在不同地区的危害性互不相同，本文引入面积(Area)、人口(Population)和GDP等变量来描述各个地区的风险差异，数据来自世界银行(World Bank)网站。直观上看，巨灾债券保障的区域面积越大，人口越多，经济越发达，巨灾造成的损失也将越大。

巨灾债券的发行日期也可能对巨灾债券的风险息差产生影响，现有文献多以2008年为界限，研究金融危机前后巨债债券价格的差异。根据实证研究结果，我们将巨灾债券的发行日期划分为三个时段：1999年1月到2005年12月，巨灾债券市场刚刚起步，由于市场不完善，巨灾债券可能存在超额收益率，风险息差较高；2007年1月到2013年12月，受全球金融危机冲击，投资者避险情绪导致超额收益率上升；2014年1月到2018年12月，经过近20年的发展，巨灾债券市场趋于成熟，超额收益率逐渐消失，风险息差也相应走低。

(二)宏观定价因子

与巨灾债券相关的三个宏观环境分别是再保险市场环境、金融市场环境以及自然环境。在巨灾债券定价模型的现有文献中，关于再保险市场环境的指标比较成熟，关于金融市场环境的指标尚需进一步讨论，而关于自然环境的指标则是本文首次提出。

Lane等最早提出再保险市场价格波动会影响巨灾债券的风险息差[5]。当再保险市场疲软时，原保险公司分出的业务较少，而再保险公司需求旺盛，愿意低价承担分出业务，此时如果巨灾债券维持较高的风险息差，原保险公司会更愿意采取再保险的方式分散风险，从而降低巨灾债券的需求，最终导致巨灾债券的风险息差下降。反之，当再保险市场坚挺时，会导致巨灾债券的风险息差上升。在实证研究中，通常采用Lane Financial公司发布的Rate on line(ROL)指标来描述再保险市场状态，ROL > 100表示再保险市场处于坚挺状态，而ROL<100表示再保险市场处于疲软状态。

为了考虑金融市场环境对巨灾债券价格的影响，Cummins等最早引入S&P500指数作为定价因子，但S&P500指数日收益率并不能很好地度量金融风险[6]。根据Basel III和Solvency II的监管要求，虽然VaR可以作为度量金融风险的指标，但VaR不满足风险度量的一致性要求。为此，Stupfler等计算了S&P500指数的负对数日收益率及其CVaR，并将其作为巨灾债券的定价因子，结果表明，发生金融危机以后，随着S&P500指数的下跌，CVaR增大，从而导致巨灾债券的风险息差上升[9]。虽然，基于S&P500指数构造的CVaR可以较好地描述金融危机对巨灾债券价格的影响，但仍存在一定问题。巨灾债券是全球市场，而S&P500指数主要反映美国金融市场环境，不能完全体现全球经济状况。此外，Stupfler等在计算CVaR时选择了90%的分位数水平，具有一定的主观性。本文综合比较了股票的百分比收益率和对数收益率，分析了它们的CVaR、变异系数以及平均数等指标在定价模型中的效果，最终采用S&P500指数日百分比收益率的年平均数作为定价因子[9]。

在研究巨灾债券定价模型的现有文献中，都忽略了与自然环境相关的其他指标。由于目前缺乏全球性的自然环境指标，本文采用美国的CEI指数作为定价因子。CEI指数的取值从0%到100%，表示该年度美国极端天气的占比。数据来自NOAA网站(http：//www.noaa.gov)。当CEI指数上升时，表示本年度的极端自然环境较多，巨灾债券所要求的风险息差也会因此而提高。

为了防止遗漏变量，本文尽可能收集了历史文献提及的定价因子，并根据实际情况提出了新的定价因子，详见表1。在实际建立回归模型时，需要根据回归系数显著性、回归模型拟合效果进行挑选定价因子，本文拟采用逐步回归的方法挑选定价因子。

表1 巨灾债券定价因子汇总表

三、定价模型

与传统线性模型相比，广义加性模型(GAM)的优点是模型形式灵活，具有更好的拟合效果和预测精度。由于巨灾债券是面向广大投资者发行，需要模型具有较高的经济解释能力。因此，本文引入分箱策略，对广义加性模型的平滑项进行离散化处理，然后建立新的广义线性模型(GLM)。

通过分箱策略对广义加性模型进行改造后获得的模型，可以看做原来模型的近似，同时兼顾了拟合效果、预测精度和经济解释能力之间的关系，对实际定价有较高的应用价值。

(一)回归模型

线性回归模型为最基础的的模型，其要求参数线性且残差服从标准正态分布。线性回归模型的一般形式为：

Y=β0+β1X1+…+βpXp

(4)

其中，Y表示因变量，X表示解释变量，p表示解释变量个数，β0，β1，…，βp表示回归系数。

广义线性模型是对线性回归模型的改进，因变量Y服从指数分布族，同时引进连接函数g(·)，其一般形式为：

(5)

其中，Y表示因变量，F表示其分布函数，μ和σ分别表示均值参数和尺度参数，g(·)表示连接函数。

广义加性模型是广义线性模型的非参数扩展，采用非参数函数对连续型解释变量进行替换，从而可以刻画因变量和特定解释变量直接的非线性关系。广义加性模型的一般形式如下：

(6)

其中，s(·)表示平滑函数，m表示平滑项个数，p表示解释变量个数。

在实际应用中，可以用R程序包mgcv估计广义加性模型的参数。在广义加性模型中，由于平滑函数s(·)的表达式过于复杂，在实际应用中缺乏直观的解释能力。故本文借鉴Henckaerts提出的方法，对连续型变量进行分箱处理，将连续型变量转化为离散型变量，然后构建更为直观、解释能力更强的广义线性模型[4]。

(二)分箱策略

决策树是一种常见的机器学习算法，具有树的形状结构，其内部节点表示某个属性判断，每个分支表示判断的输出，最后的叶节点表示分类结果。

为了将广义加性模型中的连续型变量划分为若干区间，从而将其转化为离散型变量，可以采用Grubinger等提出的进化树[14]。该方法优于其他决策树方法，能够求得全局最优解。进化树的输入变量为广义加性模型中平滑项和对于的解释变量，即si(Xi)，Xi，i=1，2，…，m。进化树的目标函数如下所示：

arg min(nln(MSE)+4α(m+1)ln(n))

(7)

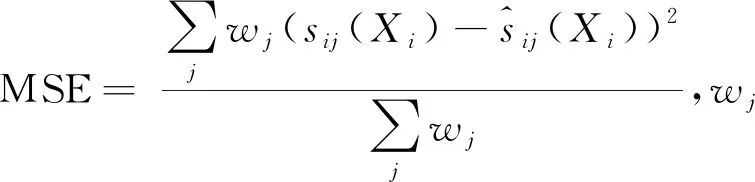
经过分箱策略处理后，连续的平滑函数si(Xi)，i=1，2，…，m，将被处理成若干段离散的线段。划分的结果为数据、模型共同驱动，操作简单。当离散化线段的数量越多，则对平滑项的近似效果越佳。

将离散线段处理成虚拟变量，替代式(6)中的平滑项，得到最终的模型为：

(8)

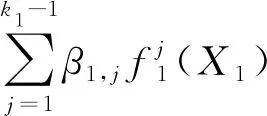
(三)模型评价

巨灾债券的风险息差定价模型除了拟合历史数据，对历史价格进行解释外，其更大的作用在于对未来发行的债券提供参考价格。为此，我们对定价模型从两个角度进行评价：

一方面是采用AIC和BIC等统计指标对模型进行评价和比较，其中AIC=-2l+2k，l表示模型的似然函数值，k表示模型的参数个数，n表示样本量。AIC和BIC的数值越小，表示模型的拟合能力越强。

另一方面是用样本外数据评估模型的预测能力，即将所有数据划分为训练集和测试集两部分，训练集的数据主要用于模型的参数估计，而测试集的数据则用来衡量模型的预测能力。常用的评价指标包括平均绝对误差(MAE)、均方根误差(RMSE)，它们的计算公式如下：

(9)

(10)

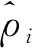
本文将采用AIC衡量模型样本内拟合效果，采用均方根误差衡量模型样本外预测能力。

四、实证研究

巨灾债券通过SPV发行，没有全球统一的交易所，二级市场的交易数据鲜有公开，因此我们主要研究巨灾债券一级市场的定价问题。本文将采用前文提及的模型和方法，对收集的样本数据进行回归分析。首先，本文先对所有数据进行实证研究，分析模型的拟合效果和定价结果；然后，本文将数据划分成训练集和测试集，采用训练集的数据进行建模，利用测试集的数据检验所有模型的预测能力，最终挑选合适的模型。

(一)数据来源

实证研究的数据来自Lane Financial LLC，Artemis和Aon Benfield三家机构，其中Lane Financial LLC每年初发布年度报告，披露巨灾债券发行的主要信息；Artemis每月披露一次巨灾债券的发行信息，可以提供触发类型、风险源、保障区域和期望损失等信息；Aon Benfield可以提供较为详细的巨灾债券评级信息。以Lane Financial LLC的最新年度报告为基准，使用Artemis和Aon Benfield发布的有关信息对其中的缺失数据进行补充，并对其他数据进行交叉验证后，得到了从1999年1月至2018年12月共计609条巨灾债券的有效发行数据。目前，大部分研究的样本数据只有200条左右，本文取得更多的样本数据，使得模型参数更稳健，方便将数据划分为训练集和测试集，验证模型的预测能力。

(二)描述性统计分析

图1是巨灾债券平均每半年的期望损失、风险息差和价格乘数的时间序列，在计算平均数时，使用巨灾债券的发行规模为权重。整体上看，巨灾债券的价格乘数有一个明显的下降趋势。在1999年至2013年，价格乘数波动较大，特别是在2000年、2005年、2008年和2011年，价格乘数都有较大幅度的上升，这些年度都伴随着较大的金融危机或者自然灾害。譬如，2000年的互联网泡沫引发股市大跌，2005年的美国卡特里娜飓风造成1 080亿美元损失，2008年发生全球金融危机，2011年日本发生9级大地震。

图1比较了巨灾债券的风险息差与期望损失，可以发现，风险息差与期望损失存在一定的正相关关系，这种相关关系在2014年以后尤为明显，表明风险息差与期望损失之间的相关性可能存在一定的时间效应。图2将数据划分为三个时间段，分别是1999年至2005年、2006年至2013年以及2014年至2018年。1999年至2005年的风险息差与期望损失具有较为明显的线性趋势；2006年至2013年的数据较为分散，表现出较高的波动性；2014年至2018年的线性趋势最为明显。

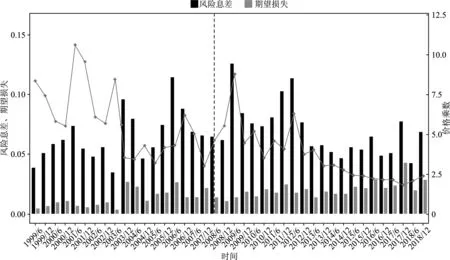
图1 巨灾债券的风险息差、期望损失和价格乘数

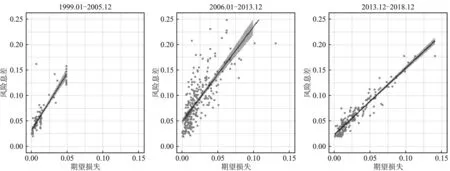
图2 风险息差与期望损失的关系

(三)模型选择与参数估计

本文的因变量为巨灾债券风险息差，解释变量为表1提及的27个定价因子。从模型的经济含义看，截距项表示巨灾债券的超额收益率。长期而言，市场将趋于均衡状态，任何收益都有对应的风险源。Braun发现采用无截距项的回归模型，更符合金融理论和实际情况[7]。

因此，本文构建无截距项的回归模型，采用逐步回归的方法，同时考虑定价因子的显著性水平，最终挑选出9个定价因子：期望损失(EL)、风险附加(Load)、再保险市场状况(ROL)、巨灾债券的信用评级(Rating)、巨灾债券的保障区域是否为高风险地区(Peak)、金融市场状况(SP500)、自然环境状况(CEIwind)以及两个关于债券发行时间的虚拟变量，Time1999—2005和Time2006—2013，β1，β2，…，β9为回归系数，线性模型的表达式如下：

ρ=β1EL+β2Load+β3Peak+β4Time1999—2005+

β5Time2006—2013+β6ROL+β7CEIwind+

β8SP500+β9Rating

(11)

从理论上讲，可以在不同的分布假设下建立风险息差的广义加性模型。通过比较不同分布的拟合效果和预测能力，最终本文选择尺度化t分布下建立风险息差的广义加性模型，并使用等值连接函数。对于均值为μ，尺度参数为θ，自由度为υ的尺度化t分布，其概率密度函数可以表示为：

(12)

在尺度化t分布假设下，经过逐步回归，最终得到关于风险息差的广义加性模型如下：

ρ=β1EL+β2Load+β3Peak+β4Time1999—2005+

β5Time2006—2013+s(ROL)+s(CEIwind)+

s(SP500)+s(Rating)

(13)

其中，β1，β2，…，β5为回归系数，s(·)为平滑函数。在计算风险附加时，使用Logit风险度量方法，选取的分位数水平为α=0.95。上述模型的参数估计结果如表2和表3所示，t分布的自由度为3.35。

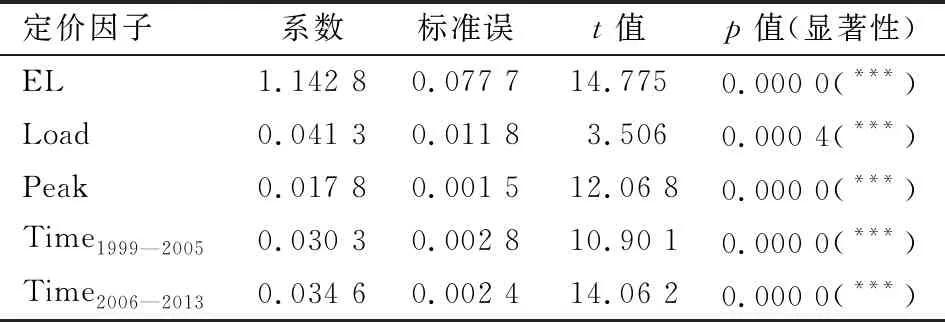
表2 广义加性模型的参数估计结果

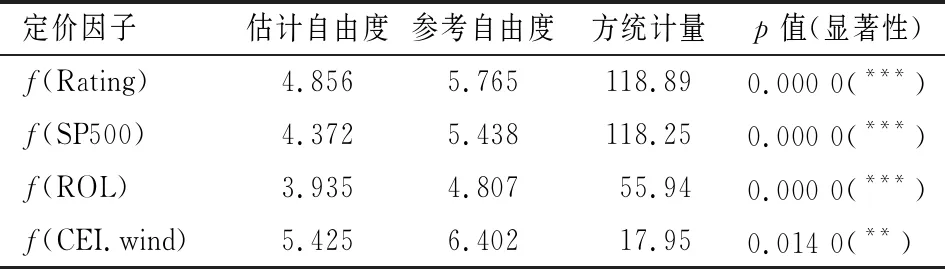
表3 广义加性模型的平滑项估计结果

表2和表3的回归结果表明，期望损失、风险附加以及巨灾债券保障区域为高风险地区的回归系数均为正值，说明这些变量与风险息差之间正向相关，符合我们的预期。巨灾债券发行时间的系数显著大于零，说明1999年1月到2005年12月和2006年1月到2013年12月，由于巨灾债券市场不完善和金融危机的冲击，巨灾债券存在超额收益，而2014年1月到2018年12月，随着巨灾债券市场趋于成熟，巨灾债券的超额收益也逐渐趋于零。

图3黑色实线为广义加性模型平滑项的趋势图，可以看出，巨灾债券的风险息差与各种定价因子之间确实存在一定的非线性关系。巨灾债券的信用评级、金融市场风险与巨灾债券风险息差存在负相关关系。巨灾债券的信用评级越差，其风险越高，则风险息差也越高；S&P500指数下跌，表明金融市场发生危机的预期提升，风险息差也会上升。再保险市场风险和自然环境状况与巨灾债券风险息差存在正相关关系，ROL指数提升，说明再保险市场需求旺盛，从而推高巨灾债券的风险息差；CEIwind指数提升，说明过去一年极端天气更为频繁和严重，影响了人们的预期，从而导致风险息差提高。

应用进化树对公式进行离散化，最终得到的广义线性模型如式(14)所示，参数估计结果如表4所示。在离散化过程中，为了保证结果的稳健性，要求每个离散化区间的样本量不少于总样本数的15%，基于AIC最小化选择的惩罚系数为α=0.5。

离散化后得到的变量都为虚拟变量，例如ROL[0.82，0.93)表示ROL取值在[0.82，0.93)时，ROL[0.82，0.93)=1；ROL取其他值时，ROL[0.82，0.93)=0，其余虚拟变量同理。最终定价模型为式(14)，其中β1，β2，…，β17为回归系数。

ρ=β1EL+β2Load+β3ROL[0.82，0.93)+

β4ROL[0.93，1.01)+β5ROL[1.01，1.23)+

β6ROL[1.23，1.44)+β7ROL[1.44，1.83)+

β8Rating[1，4)+β9Rating[4，6)+β10Rating[6，11)+

β11CEIwind[0.027，0.061)+β12CEIwind[0.061，0.199)+

β13CEIwind[0.199，0.933]+β14SP500[-0.000 1，0.000 1)+

β14SP500[0.000 1，0.001 7)+β15Peak+

β16Time1999—2005+β17Time2006—2013

(14)

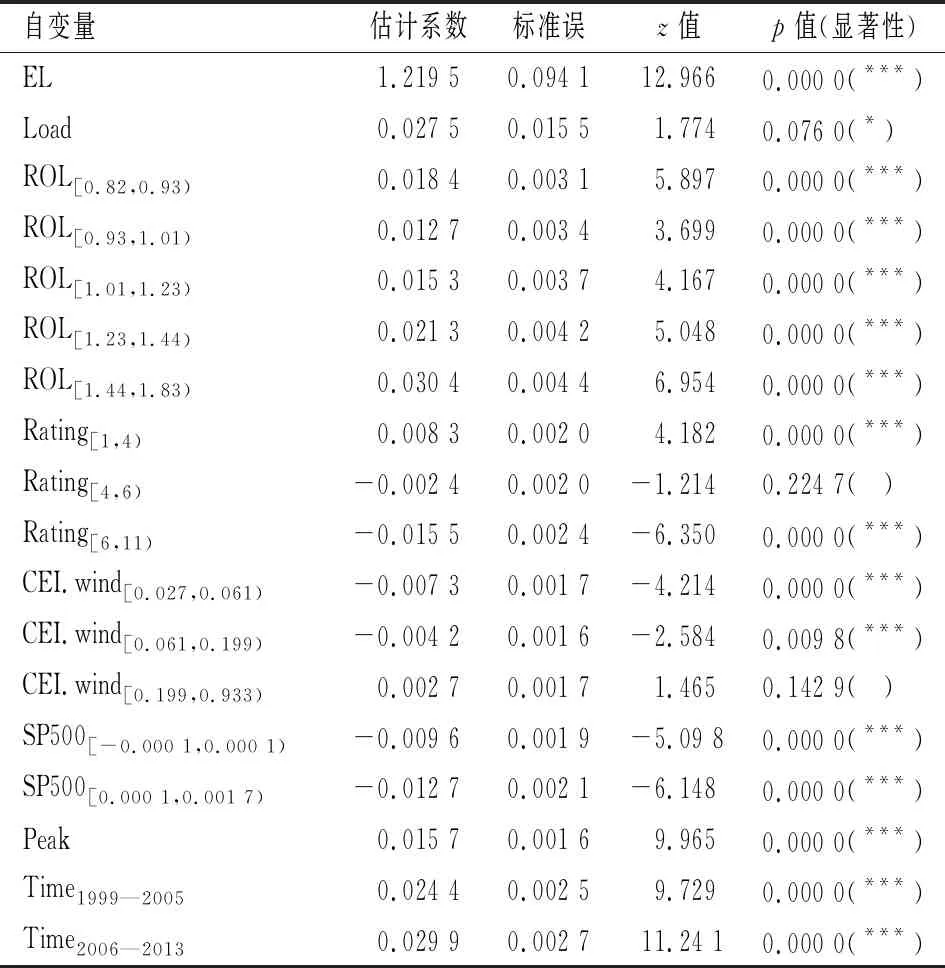
表4 广义线性模型定价模型的参数估计值

表4为分箱处理后得到广义线性模型的回归结果，虽然损失部分精度，但提高了模型的解释性，可以根据具体实际情况向投资者解释巨债债券的定价结果。期望损失、风险附加、巨灾债券保障区域是否为高风险地区以及巨灾债券发行时间的系数显著大于零，数值大小与广义加性模型较为接近。巨灾债券的信用评级、金融市场风险与巨灾债券风险息差存在负相关关系，再保险市场风险和自然环境状况与巨灾债券风险息差存在正相关关系，符合预期。

图3黑色圆点为广义线性模型的回归系数，实线为广义加性模型的平滑项拟合值，竖虚线为应用进化树划分的离散化区间的端点。可以发现，在大部分情况下，广义线性模型的回归系数和广义加性模型的平滑项数值较为接近。

图4给出了广义线性模型对于全部数据回归的检验结果，广义加性模型的检验结果优于广义线性模型。图4的QQ图在总体上接近对角线，基本服从正态分布，说明定价模型对总体数据的拟合效果良好。

图3 广义加性模型与广义线性模型的系数对比

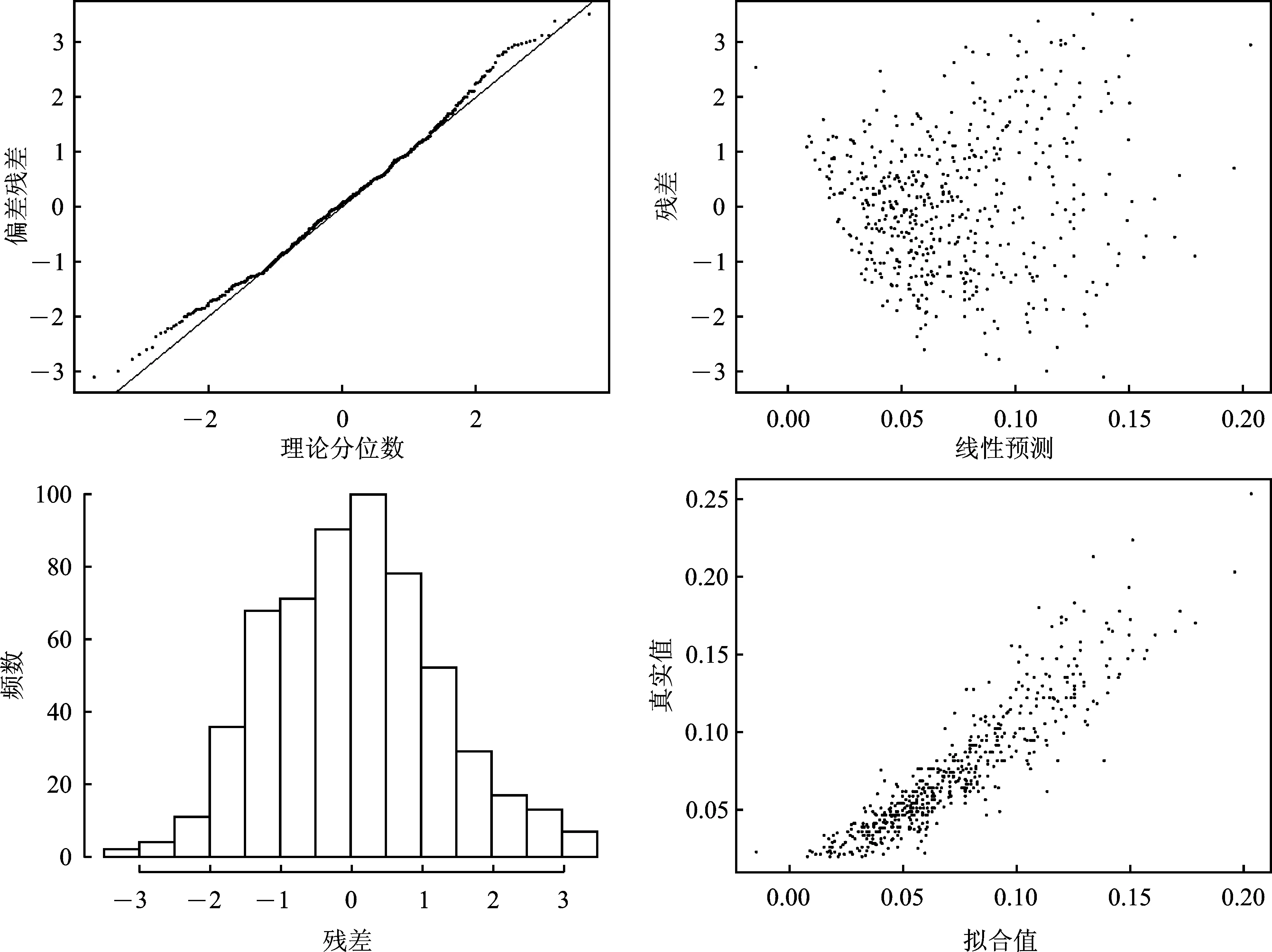
图4 广义线性模型的检验

图5 广义加性模型与广义线性模型预测的风险息差对比

图5比较了广义加性模型和广义线性模型拟合的风险息差，结果表明，经过分箱技术处理过的广义线性模型与广义加性模型的预测结果非常接近。

(四)结果比较

现有文献提出了多种不同的巨灾债券风险息差定价模型，为了比较它们的预测效果，按照债券发行的时间顺序，本文将所有样本数据按照70∶30的比例划分为训练集和测试集，前期的70%数据为训练集，后期的30%为测试集。在模型比较中，样本内的评价指标使用AIC，样本外评价指标使用均方根误差。

表5给出了对各种定价模型的比较结果，在该表的比较中，本文最终模型为经过分箱策略后得到的广义线性模型。在样本内，本文模型的AIC最小，表明其对训练集的拟合效果最好；在样本外，本文模型的均方根误差最小，表明其样本外的预测能力最强。为了更方便和投资者介绍产品，本文推荐采用式(14)进行定价，能够同时兼具预测能力和经济解释能力。因此，对巨灾债券风险息差进行定价时，本文提出的模型具有相对优势。

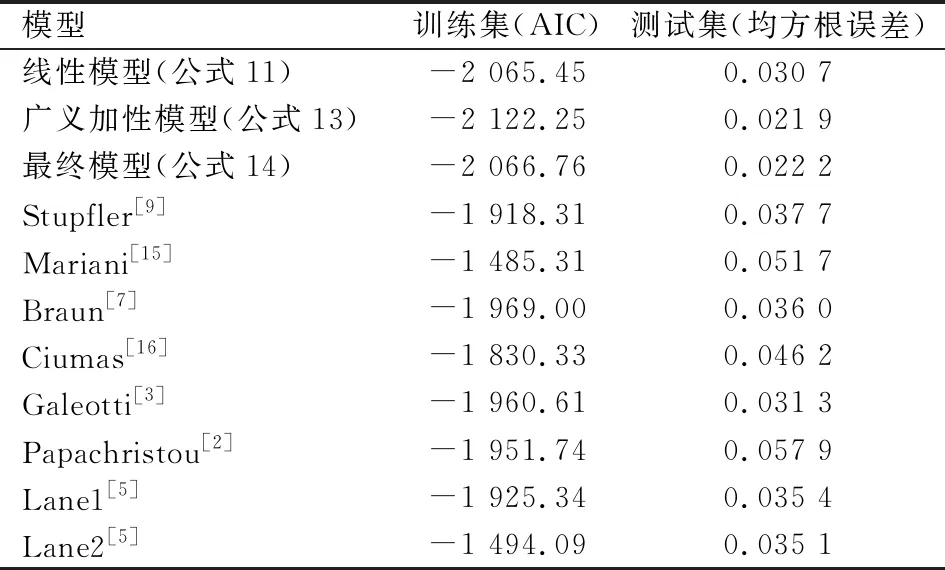
表5 风险息差定价模型的比较

表6 现有文献中主要的风险息差定价模型

表6中各种变量的含义如下：SP50090表示基于S&P500指数计算的90%水平下的CVaR风险度量值；Libor表示伦敦银行间隔夜拆借利率；Cspread.bb表示BB等级的公司债的信用价差； PFL表示其起赔概率；CEL为期望损失与PFL之比；PLL表示全损概率；BB是虚拟变量，其中BB=1表示巨灾债券的评级为BB级，BB=0表示其他情况；ABBB是虚拟变量，ABBB=1表示巨灾债券的评级为A级和BBB级；Term12是虚拟变量，其中Term12=1表示巨灾债券的期限介于1年到2年之间；f1(x)和f2(x)表示平滑函数；Time表示巨灾债券的发行时间；PT是虚拟变量，PT=1表示风险源是美国的飓风，PT=2表示风险源是美国地区的地震，PT=3表示其他情况。

五、结 论

本文主要研究了巨灾债券的风险息差及其定价模型，探讨了数据搜集、模型设定和定价因子的选择等问题，并与现有文献中的定价模型进行了比较。通过整合三家公司的公开数据库，收集整理了609条巨灾债券一级市场的发行数据，增加了样本量；在定价模型中引入了若干个新的定价因子，包括基于Logit风险度量值的风险附加、巨灾风险指数等；在风险息差服从尺度化t分布的假设下，建立了更加灵活、更加符合现实情况的广义加性模型。为了提高定价模型的解释能力，通过进化树将广义加性模型转化为广义线性模型，最终得到了兼具准确性和解释性的风险息差定价模型。与现有文献中的风险息差定价模型相比，本文建立的定价模型在拟合优度和预测能力方面均有显著提高。实证研究结果表明，期望损失、基于Logit风险度量的风险附加、再保险市场状况、巨灾债券的发行时间、巨灾债券的信用评级、巨灾债券保障范围的风险情况、自然环境状况和金融市场状况对定价有重要影响。