运用线性规划思想探求最值一例

安徽省灵璧师范学校 (234200) 陈 伟

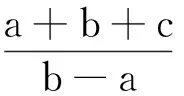
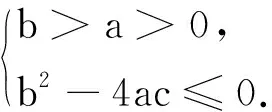
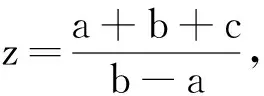
问题又转化为：在约束条件

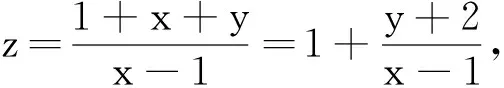
图1

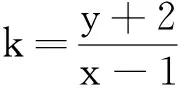
当然，本题转化后，还可以利用基本不等式求解.

综上所见，本题解题过程是依据给定的条件和要解决的问题，运用等价转化、换元、化归等数学思想方法，把有关约束条件和目标函数用逻辑关系恰当地表示出来，再借鉴规划思想求目标函数的最优值.我们在教学中适当向学生加以介绍，不仅可很好地激发学生思维灵活性和创造性、提升学生解题能力，还能使学生体会到知识迁移的美妙、问题化归的魅力．