有图数量积相关问题的求解策略

江苏省海门中学 (226100) 渠怀莲

向量具有数与形的双重身份，是联系代数与几何的桥梁，尤其是数量积问题的求解更是体现大小与方向的两大要素.在平面几何图形给定后，求解相关的数量积问题，我们可以有一下几种处理问题的策略：向量的三种表示对应三种运算，图形表示即构造几何图形直线与圆、解三角形等；字母表示即基底法；坐标表示即建立平面直角坐标系解析法.

图1

解法1:如图1，共起点向量基底化，旨在使学生产生“基底”意识，图形中向量“基底”是表示向量的基本方法，转化过程主要运用平行四边形法则和三角形法则.

解法2:两边点乘同一个向量，利用数量积的几何意义——投影求解.

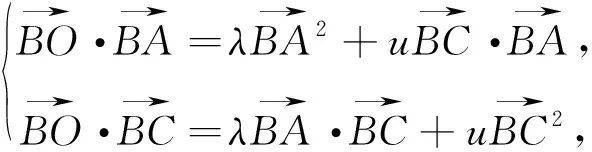
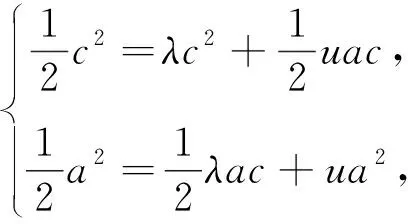
图2

解：建系法是平面向量“代数”化的体现，将向量用坐标表示，实现向量式向数量式的转化，建系时往往要借助平面向量中有关垂直向量的关系来处理，以此对应的向量为坐标轴所在的直线，或利用对称性建系，不同的建系会导致不同的运算效果.

注：此题若用基底法很难实现问题的转化，因为个向量的模均未知.

图3

解法1:利用几何确定点O的位置，利用平面几何图形的结构特点，运用简单的几何性质，结合向量运算的几何意义(三角形法则或平行四边形法则等)来分析与求解，往往可以使解题更直观，更简捷，便于判断与操作.

解法2:建立平面直角坐标系，引入角元，利用三角函数法，是平面向量问题在解三角形中的强有理的方法，是平面向量问题向直角三角形或化斜为直充分体现.借助三角函数的定义、三角恒等变换公式等，结合平面向量的数量积公式等加以有效转化与求解.

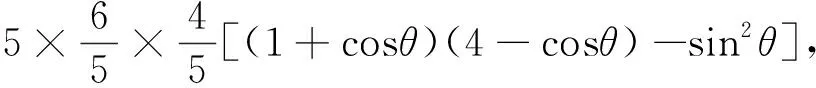
结语：在培养学生在解决图形中的数量积问题能够灵活地转化，让学生形成正确的几何性质、基底意识即解析思想方法.学生解题“意识目标”的培养，是需要老师在一段时间内或者长时间内不断地渗透强化形成的.希望学生做到以原型启发为突破口，深入研究试题的命制方向进行拓展和深化，使学生在不断地积累沉淀的过程中加深对知识的解，增强学生学好数学的信心，提高学生的学习数学的兴趣.