半主动激光导引头光学系统设计及线性度分析

蒲小琴，董全林*，余子箫，张斯明，邵静怡，刘业楠，王军伟

（1.北京航空航天大学 仪器科学与光电工程学院，北京100191；2.中国空间技术研究院；3.北京卫星环境工程研究所：北京100094）

0 引言

现代实战数据表明，精确制导武器已成为高端技术战争的主要杀伤工具[1]。导引头作为激光制导武器的核心器件，其性能好坏将直接影响激光制导武器的打击效果。导引头由接收光学系统、探测器及电子舱组成，其中光学系统作为导引头的重要部件，其主要功能是将目标反射的激光束汇聚到探测器上，通过对探测器接收到的光斑照射能量的处理得到目标的方位信息，再由控制舱根据目标方位信息控制弹体飞行姿态实现对目标的准确打击。由光学系统汇聚到探测器上的光斑质量决定了探测方位的准确性[2-3]，故有必要对光学系统及其汇聚光斑能量分布线性度进行设计研究。

本文基于激光导引头的工作原理，推导从探测器接收的目标激光信号中得到目标方位俯仰角信息的过程，分析光斑能量的均匀性区间。在此基础上设计3款光学系统，并在特定线性视场角下对它们的光斑能量进行分析比较，希望能以较简单的结构获得满足光斑能量线性度及线性视场角要求的光学系统。

1 激光导引头工作原理

半主动激光导引头的工作原理是由弹外激光指示器发出经特定周期编码的激光照射到目标物体上，当制导导弹飞近至满足导引头捕获目标作用距离时，导引头光学系统自动搜索并捕获目标物体或目标周边环境漫反射的激光信号于四象限探测器上[4]，通过对探测器上光斑能量分布状况进行分析处理，得到目标反射激光在四象限探测器上成像的位置信息；控制平台根据该位置信息控制导弹的垂直尾舵或水平尾舵以调整导弹的飞行姿态，不断修正其飞行方向直至准确瞄准攻击目标，从而实现制导功能。

四象限探测器是由4个光敏二极管组成的感光面阵列，每象限对外有1路电流信号输出，影响信号大小的因素包括被象限分割的光斑面积大小和光斑照射的强弱程度[5]。目标反射激光经光学系统汇聚后被四象限探测器探测，将4个象限输出的电流信号进行和差处理就可以得到光斑中心在探测器上的位置信息，即目标相对于弹体的位置信息。为了更好地得到目标光斑，需将探测器放置于光学系统离焦处，其原理如图1所示，其中探测器直径为2R，光斑直径为2r，光斑中心位置为(x,y)，4个象限分别用A、B、C、D表示，它们的输出光生电流分别为IA、IB、IC、ID。

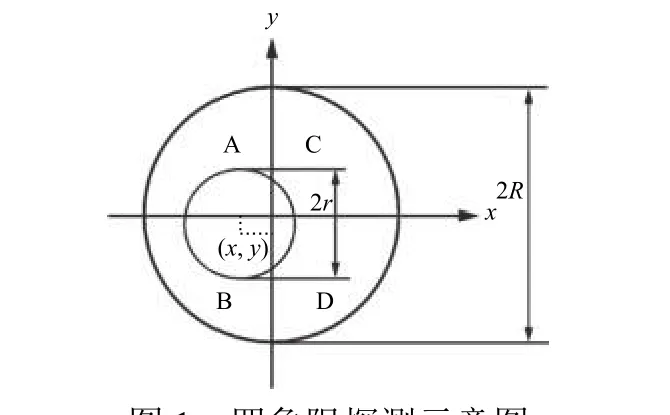
图1 四象限探测示意图Fig.1 Schematic diagram of four quadrant detection

式中：Kx和Ky是比例系数；Ix与Iy分别为x、y方向上的偏差信号。

假设光斑能量分布均匀，分析光斑尺寸及光斑中心位置与探测器的内在联系，并考虑接收光斑的线性度问题，得到偏差信号表达式：

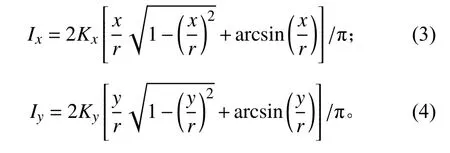
使用MatLab工具对式(4)进行归一化处理，结合探测器APD的直径，给出的角度位置-电流偏差（y-Iy）曲线如图2所示。由图可见，偏差信号Iy与y为非线性关系（显然Ix与x亦为非线性关系），且式(3)、式(4)是在整个光斑能量分布均匀的前提下得到的，因此需要对光斑能量分布及线性度进行分析研究。

图2 角度位置-电流偏差（y-Iy）曲线Fig.2 Angular position vs.current deviation

式中：f为透镜组焦距；Δf为离焦量。

控制舱通过对方位角和俯仰角的控制来实现对整个弹体姿态的调整。

2 光斑能量分布及线性度

当光斑能量分布均匀且方位角α与俯仰角β较小时，偏差信号Ix与Iy分别与α、β为线性关系。但实际上光斑能量分布并不均匀，光学系统常会因为线性度不足而影响激光导引头的制导精度，因此讨论光斑能量分布对于线性度的影响非常重要。像差的变化会改变能量分布，实际光学系统在不同方位角或俯仰角下的像差不同，但只要将像差的变化量控制在一定范围内，就可忽略它们对能量分布的影响。

设光斑的半径r为1，辐射通量W归一化为1，光斑的能量分布旋转对称，取r处的一圆环宽度为dr，如图3所示。

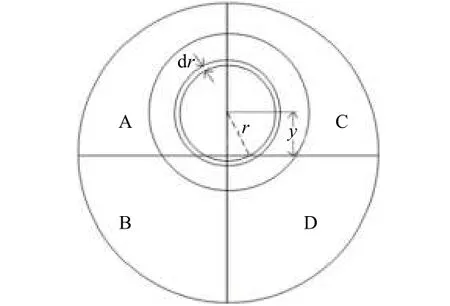
图3 光斑能量分布示意图Fig.3 Schematic diagram of spot energy distribution

四象限探测器将接收到的光斑辐射通量W转换为电流信号，设偏差信号Ix、Iy与探测器4个象限上的辐射通量WA、WB、WC、WD间的关系式为：

设A、C象限的光通量为Wup=WC+WA，B、D象限的光通量为Wdw=WD+WB，则有

用MatLab对光斑照度与半径关系进行处理，得到过拟合后的照度沿径向分布曲线如图4所示。

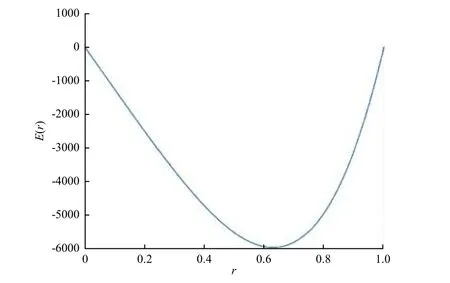
图4 过拟合照度径向分布曲线Fig.4 Radial distribution of overfitted irradiance curve

由图4可见，随着光斑半径的增大，过拟合后的光斑照度先减小后增大，光斑能量分布没有线性区域。出现这种现象是因为KTK接近奇异矩阵使得曲线过拟合。加入正则化约束并进行优化，令得到图5所示归一化曲线。可以看出，光斑能量分布存在一个线性区域，即相对于半径r的0～0.6的区间范围内光斑能量分布基本均匀，而在0.6～1的区间内，照度沿半径增大方向而增强。

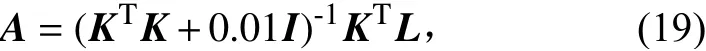
图5 照度径向分布归一化曲线Fig.5 Radial distribution of irradiance

3 光学系统的设计及验证

半主动激光导引头利用光学系统将目标激光信号汇聚于探测器上，通过分析激光光斑在探测器上的位置分布来获得制导导弹相对于目标的偏差信号[6]，主要关注的是光斑的稳定性及能量分布均匀性，因此导引头的光学系统是非成像系统。为了确保信号被探测器有效接收，光学系统需有较高的透过率，一般应大于等于80%。提高光学系统透过率的主要途径有2个：一是提高系统组成镜片的透过率，选用高透过率的材料或使用增透膜；二是从系统设计着手，让系统的结构尽量简单，但由此往往引起系统线性度的下降[7]，须进行巧妙的设计才能在保证线性度的前提下获得较高的透过率。

光学系统的主要指标要求为：

1）工作波段：(1064±2.5)nm；

2）瞬时视场角：±15°±0.5°，线性区不小于±8°；

3）工作方式：单四象限；

4）光敏面大小：ϕ14mm；

5）入瞳直径：30mm；

6）系统畸变：≤1%。

可见，需要设计的光学系统是针对特定波长的单色性光学系统，而且激光信号的色差可以忽略不计。下文将根据一定的基础结构，进行光学系统设计并分析其能量分布状况与线性度的关系。

3.1 单透镜光学系统

用简单的结构来获得较高的线性度不是一件容易的事情。因为系统结构简单，参变量少，且系统的线性度与构型直接相关，若构型不合理将严重影响系统线性度。鉴于此，系统构型优化设计就显得尤为重要[8]。我们以透镜的弯曲构思了多种方案，然后从中选取较优的构型。经过视场权重配置、评价函数配置、像差处理及锥形优化、离焦等得到的单片透镜光学系统（见图6），由球罩、单色滤光片和单片透镜组成，其中透镜的焦距为25 mm。将整个系统转化到NSC（non sequential component）模式，利用光线追迹得到单透镜光学系统照度图（图7）。

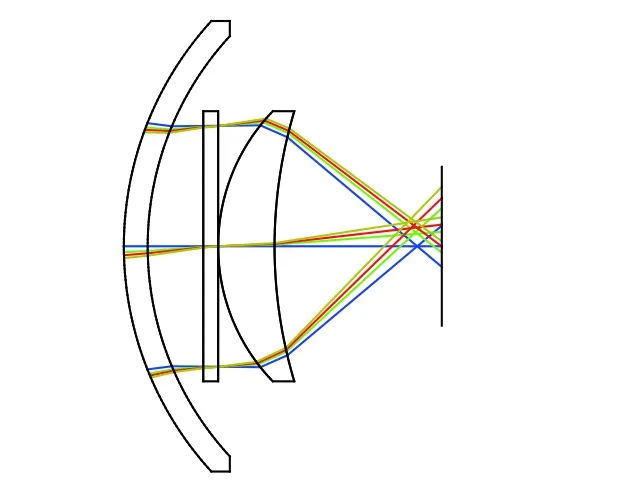
图6 单透镜光学系统Fig.6 The single-lensoptical system

图7 单透镜光学系统照度图Fig.7 Irradiance map of the single-lensoptical system

用MatLab读取照度数据，参考式(2)并取Ky=1即可算出Iy，绘制单透镜光学系统的正向俯仰角与输出电信号（β-Iy）的线性拟合曲线如图8所示。由于光斑具对称性，β取线性视场角0°～8°，间隔0.5°，β及Iy的具体数值见表1。

图8 单透镜光学系统俯仰角与输出电信号线性拟合Fig.8 Linear fitting of the pitch angle of the single-lens optical system w ith the output electrical signal

表1 单透镜光学系统俯仰角与输出电流数据Table 1 Pitch angle and output current data for the single-lensoptical system

由图8可以看出，在决定系数R2=0.979 1时，直线拟合效果较差；而改用多项式拟合、决定系数R2=0.998 8时的效果较好（见图9）。可见，对于单透镜光学系统而言，在线性视场角为±8°时，整个探测器输出信号的线性度低，不能达到系统设计要求。

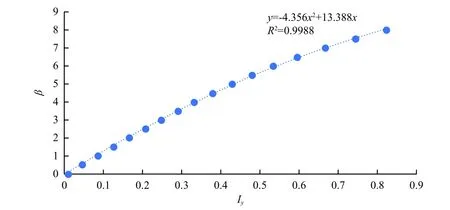
图9 单透镜光学系统俯仰角与输出电信号多项式拟合Fig.9 Polynomial fitting of the pitch angle of the single-lens optical system w ith the output electrical signal

3.2 双透镜光学系统

从单透镜光学系统的设计中可以看出，由于变量有限，很难将球差控制在一个比较理想的水平，慧差也无法消除，因此由照度数据得到俯仰角与输出电信号的线性度不高，需要改进设计。为了消除球差得到更为理想的线性光学系统，常用的方法是采用胶合镜或2片分立的正负透镜组合[9]。导引头使用的是激光窄光束，因此采用正负透镜组合可以很大程度上消除球差，保证光学系统设计质量。设计优化后的双透镜光学系统如图10所示，由球罩、单色滤光片和双分离透镜组成，系统的入瞳直径为30mm。通过非序列分析，得到双透镜光学系统照度图（图11）。

由图11可以看出，光斑的照度分布为边缘高、中间低，且中间部分分布均匀，符合光斑能量分布线性区的关系。运用单片透镜的分析方法，绘制双透镜光学系统β-Iy线性拟合曲线如图12所示，β及Iy的具体数值见表2。

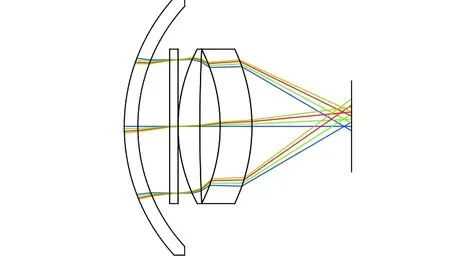
图10 双透镜光学系统Fig.10 The double-lensoptical system

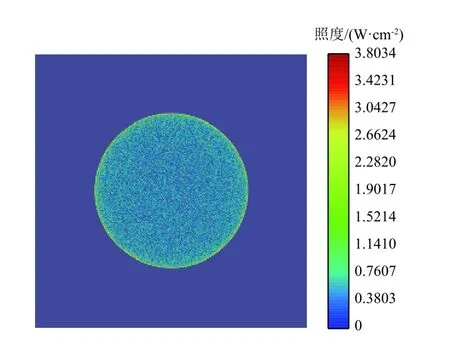
图11 双透镜光学系统照度图Fig.11 Irradiancemap of the double-lens optical system

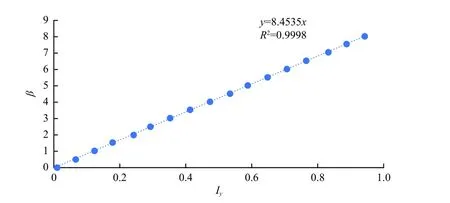
图12 双透镜光学系统的β-Iy 线性拟合曲线Fig.12 Linear fitting of β-Iy curve for the double-lens optical system

表2 双透镜光学系统俯仰角与输出电流数据Table 2 Pitch angle and output current data for the double-lensoptical system

由图12可以看出，在视场角±8°范围内，决定系数R2=0.999 8时，线性拟合效果较好，说明光斑能量分布符合上述结论，双透镜光学系统的线性度良好。

3.3 三透镜光学系统

双透镜光学系统采用正负透镜组合，球差得到了很大程度的消除，慧差也可忽略不计，因此由照度数据得到俯仰角与输出电信号的线性度较高。为得到满足系统指标要求的结构简单型光学系统，继续设计了三透镜光学系统与上述单、双透镜光学系统进行对比分析，3片透镜比2片透镜多了4个变量（第3片透镜的2个表面的曲率半径、透镜厚度以及其与第2片透镜的距离），因此三透镜光学系统可以比双透镜光学系统更好地调整像差。设计优化后的三透镜光学系统如图13所示，由球罩、单色滤光片和3片透镜组成，系统入瞳直径为30mm。通过非序列分析，得到三透镜光学系统照度图（图14）。

运用同样的分析方法，绘制三透镜光学系统β-Iy线性拟合曲线如图15所示，β及Iy的具体数值见表3。

由图15可以看出，在视场角±8°范围内，决定系数R2=0.999 8时，线性拟合效果较好，说明光斑能量分布符合上述结论，三透镜光学系统的线性度良好。

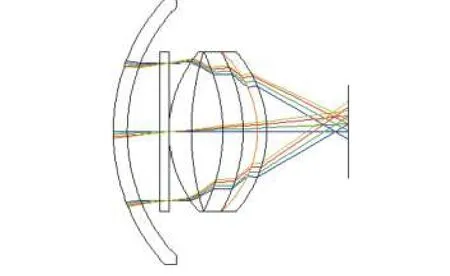
图13 三透镜光学系统Fig.13 The triple-lensopticalsystem

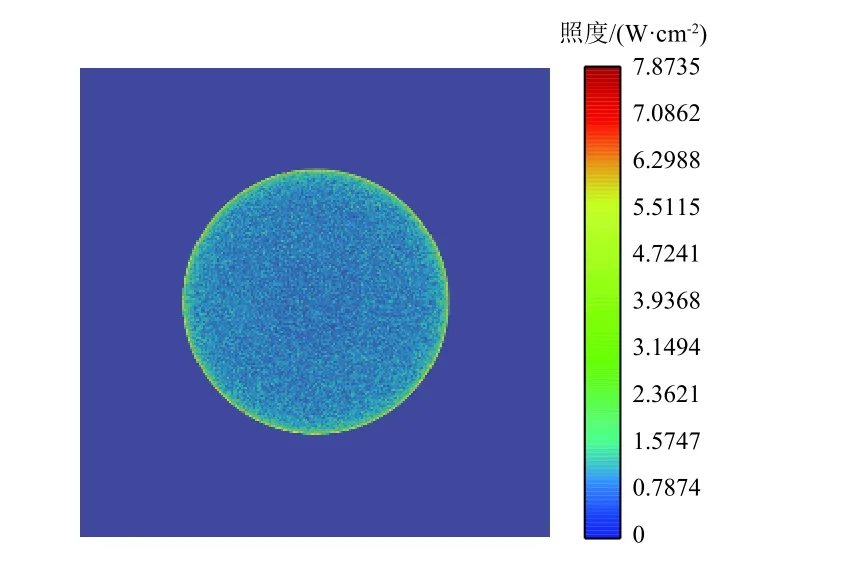
图14 三透镜光学系统照度图Fig.14 Irradiance map of the triple-lensoptical system

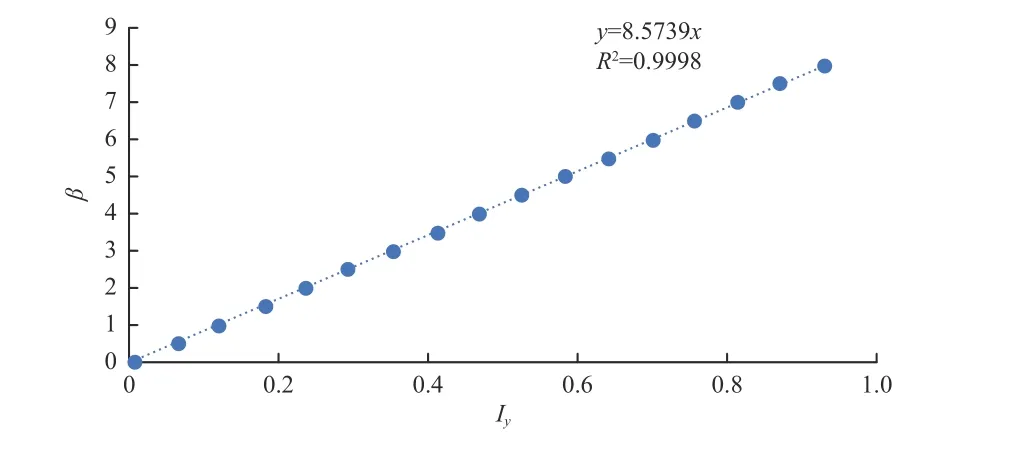
图15 三透镜光学系统的β-Iy 线性拟合曲线Fig.15 Linear fitting of β-Iy curve for the triple-lens optical system

表3 三透镜光学系统俯仰角与输出电流数据Table 3 Pitch angle and output current data for the triple-lensopticalsystem

3.4 小结

对比上述3个光学系统，单透镜光学系统结构简单，但因为参数少，像差调节能力低，优化效果不明显，不能同时满足光斑能量线性度要求及线性视场角±8°的要求，因此需要进行改进。三透镜光学系统与双透镜光学系统的性能相近，都可以实现很好的线性度，但是三透镜光学系统结构更复杂，质量更大，对光信号的衰减也更大，与双透镜光学系统相比没有优势，后者更适合应用于激光导引头。

4 结束语

光学系统作为激光导引头接收目标信息的唯一渠道，对制导精度有着重要影响。本文基于激光导引头的工作原理，分析了光学系统所汇聚的光斑能量照度分布与线性区间的关系，并用MatLab对照度曲线进行计算拟合，得到实际光斑能量分布的均匀性区间；根据光学系统的指标要求，设计了3款不同的光学系统来验证其能否满足在线性视场角±8°的前提下，光斑能量照度曲线也符合线性度要求。最后得到在±15°视场角中线性视场角为±8°且照度拟合曲线符合线性度要求的双透镜光学系统。