一种描述减振器滞回特性的Bouc-Wen改进模型

赵义伟，刘永强，杨绍普，陈祖晨

1) 石家庄铁道大学交通运输学院，石家庄 050043 2) 石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043 3) 石家庄铁道大学机械工程学院，石家庄 050043

当前，诸多专家学者们将精力都投入到磁流变减振器的研究当中[1-7]. 其作用大体和传统减振器相同，即抑制物体振动. 但是其构造和传统减振器大不相同. 磁流变阻尼器作为目前较为新型的减振器，有着传统减振器不能比拟的优点. 它的阻尼系数可以连续调节，结构简单紧凑. 磁流变减振器需要很小的电流或电压就可正常工作. 其中，研究减振器滞回特性的建模是基础，同时也是一个关键的环节. 只有根据减振器滞回特性，并用数学模型描述出来，才能进行接下来的减振器仿真设计. 因为磁流变减振器阻尼力特性呈强烈非线性并带有滞回环, 用数学模型精确简洁地描述其特性是比较困难的. 现在常用的减振器数学模型有Bouc-Wen模型[8-9]、Bingham模型[10-12]、多项式模型[13-14]等. Bouc-Wen模型能够很好地反映MRD的动态性能，同时能较好地反映低速时的滞回情况，且模拟出的滞回曲线较为平滑. 因此论文采用此模型来展开研究.

Bouc-Wen模型是1997年由Bouc和Wen提出的，是应用比较广泛的一种模型，受到国内外许多专家学者的关注. 文献[15]设计了一种磁流变减振器，建立其Bouc-Wen模型，并将其应用于列车半主动悬挂系统，并与被动悬挂系统进行了对比. 文献[16]对Bouc-Wen模型不能模拟带有力滞后现象的滞回环这一不足进行研究，提出了用Bouc-Wen的改进模型BWBN来模拟滞回环，取得了较好的效果. 文献[17]针对Bouc-Wen模型无法表述单出杆减振器中蓄能器造成的阻尼力偏置这一现象，提出了一种改进的Bouc-Wen模型，并验证了其正确性. 文献[18]对Bouc-Wen模型进行改进，并用来描述钢板装配式屈曲约束支撑（BRB）的滞回特性，并与试验数据进行了对比，验证了其有效性. 文献[19]设计了一种应用于汽车悬架系统上的磁流变减振器，并用Bouc-Wen模型描述了其滞回特性，最后将其应用在四分之一悬架模型上，进行了半主动控制分析. 上述文献对Bouc-Wen模型都进行了不同程度的研究与应用，但是大多数都是在特定的或者识别激励幅值下进行研究，对非识别激励幅值下Bouc-Wen模型是否能够准确描述出减振器滞回特性没有进行验证研究. 文献[20]针对Bouc-Wen模型提出了一种参数识别方法，并对模型在不同激励幅值下进行验证，发现 Bouc-Wen 模型对激励幅值较敏感，在非识别激励幅值情况下阻尼力精度较差，且阻尼力越大此问题越明显. 这种问题会影响模型在悬架等减振系统中的仿真应用，但针对此问题的研究较少. 因此，论文对 Bouc-Wen模型进行改进，对其进行参数识别与仿真验证，来重点解决此问题. 论文的研究目的是，改进Bouc-Wen模型，使其能够在非识别激励幅值下模拟出的阻尼力更接近于实际阻尼力值，使其更具有实用性，为其应用于车辆悬架仿真中打下基础.

1 Bouc-Wen模型及其不足

Bouc-Wen模型可以模拟多种不同类型的滞回特性曲线，能够较准确地描述磁流变减振器在低速区的非线性滞回特性. 其结构示意图如图1所示. 其数学模型描述为

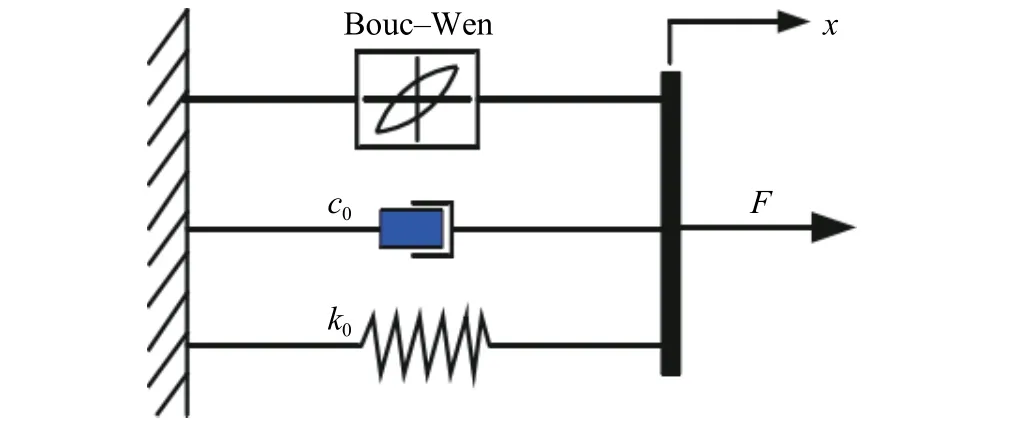
图1 Bouc-Wen模型示意图Fig.1 Bouc-Wen model schematic

用Simulink软件建立Bouc-Wen模型，如图2所示. 文献[20]对Bouc-Wen模型进行了详细的仿真验证，并指出了模型存在的不足. Bouc-Wen模型在识别的激励幅值下，能够准确的描述出阻尼力滞回特性，但是在非识别激励振幅下不能够准确地描述出滞回特性. 在仿真应用中，激励幅值往往不是特定的，而是随机的连续变化的. 因此，Bouc-Wen模型在激励振幅为连续变化的系统中，会给系统响应带来一定的误差，从而影响仿真结果.此外，试验得到的阻尼力滞回环曲线不规则时，Bouc-Wen模型不能够很准确地描述出来[16].

图2 Simulink建立的Bouc-Wen模型Fig.2 Bouc-Wen model established by Simulink

2 新型Bouc-Wen改进模型

为了更好地描述出阻尼力滞回特性曲线弥补Bouc-Wen模型的缺点，文章将此数学模型中的项用另外一种形式来表示，即用滞回环斜率与阻尼力的函数关系来模拟滞回特性，此方法灵活性较强，有着更为广泛的应用. Ni等[21]利用Dunem微分算子对一种线圈隔振器的非线性滞回特性建立了非参数模型，采用的滞回曲线方程如下：

此方程也可以写成

然而，磁流变阻尼器的滞回特性曲线和线圈隔振器的有着很大区别. 本文对其进行改进，可以得到

此方程整理一下可得

缺铜发生原因：在淋溶的酸性沙质土、石灰性沙质土、沙质砖红土壤、酸性腐泥土壤易发生缺铜。过量使用氮或磷和严重缺锌也会引起缺铜。土壤瘦瘠、土层浅薄、底层有硬盘和排水不畅也能引起铜素缺乏。

其中，U为试验得到的阻尼力，N；为试验得到的阻尼器滞回环的斜率与阻尼力的函数关系式，将阻尼器滞回环分为四段，即共有四个函数关系式，即，进一步可得到

通过观察，滞回环的斜率与阻尼力的关系可以用许多类型的初等函数来表示，如正弦函数、多项式函数、幂函数等，还可以用分段函数，从而模拟出不同形状的滞回环[22]，例如含滑移捏拢效应、刚度退化等滞回特性. 论文采用二次多项式来表示，即

针对Bouc-Wen模型对非识别激励幅值的变化比较敏感[20]这一问题，对模型继续进行修正.假如识别的曲线在激励幅值为10 mm的情况下，识别出的曲线与试验曲线具有准确的吻合度，然而当幅值为5 mm时，阻尼力衰减的过快，或者当幅值为15 mm时，阻尼力增大的过快. 修正的原理就是：当振幅变小时，模型能够延缓力的衰减，当振幅变大时，能够抑制阻尼力快速增大. 因此，可以考虑在模型阻尼力公式（2）中引入一个修正力.如果模型中引入的修正力为一常值，经过参数识别后，此常数项会分担阻尼力数值的一部分，因此阻尼力在不同幅值下变化就会缓慢许多，即模型对振幅的敏感度下降. 但如果引入常数项会破坏滞回环的光滑性和连续性. 因此，为了保证滞回环的光滑性和连续性，论文采用指数函数作为修正项，因此公式（2）可变为

其中，δF=b·sgn(x˙)·e-|x˙|；b为待优化参数.

改进后的新模型具有17个待识别参数. 接下来对修正后的模型进行参数识别.

3 MRD性能试验及模型参数识别

3.1 MRD特性试验分析

采用材料疲劳性能测试试验台 MTS793 对磁流变阻尼器进行力学特性试验. 如图3所示. 对阻尼器采用正弦信号激励进行加载. 按不同频率和幅值分为8组：（0.5 Hz，5 mm），（1.0 Hz，5 mm），（1.5 Hz，5 mm），（0.5 Hz，10 mm），（1.0 Hz，10 mm），（1.5 Hz，10 mm），（0.5 Hz，15 mm），（0.5 Hz，20 mm）.每组工况下，给阻尼器以不同的电流信号. 该阻尼器最大电流允许值为2.5 A，因此电流可分为六档：0，0.5，1.0，1.5，2.0，2.5 A. 最后，将采集得到的数据进行处理，并画出振幅和频率分别为10 mm、0.5 Hz且不同电流情况下的力-位移曲线，如图4所示.

图3 试验装置及减振器Fig.3 Testing device and shock absorber

3.2 模型参数识别方法

新模型包含有17个未知参数，需要对模型中的各个参数进行识别. 论文采用的是GA-PS识别算法[23-25]. Holland教授在1962年提出了遗传算法（Genetic algorithm）. 遗传算法优点是可以解决其他的一些标准优化算法无法解决的问题，比如目标函数为不连续、不可微等等. 遗传算法的全局搜索能力较强，能在较为宽广的范围内快速识别到需要的解. 但是遗传算法的缺点是容易过早收敛从而陷入局部最优解. 利用matlab表述为

其中，c表示被识别参数的个数；LB和UB分别表示参数的下界和上界；OPS表示其他选项设置.

图4 不同电流下的阻尼力曲线图Fig.4 Damping force curves at different currents

模式搜索法（Pattern search）是一种直接搜索算法，其目标函数不一定可微也可能是非连续. 模式搜索法的优点是可以快速地得到全局的最优解.尽管模式搜索法的计算效率高速度快，但是它的缺点在于过度地依赖初值，单独使用的时候效果不是很好. 利用matlab表述为

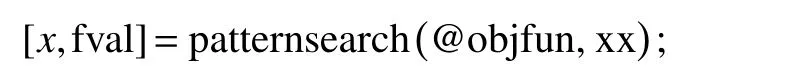
其中，fval代表目标函数值；xx代表被识别参数初始值.

综合分析可知，传统遗传算法容易陷入局部最优解，而模式搜索法对初值具有依赖性，因此采用这种联合方法既考虑了遗传算法易得到局部最优解也考虑了模式搜索法的初始值依赖性，充分利用二者的优势，快速得到参数识别所需要的全局最优解，识别流程图如图5所示.

图5 基于GA和PS的参数识别过程Fig.5 Parameter identification process based on GA and PS

3.3 识别结果及验证

采用幅值10 mm 频率0.5 Hz 激励的试验数据对Simulink搭建的新型改进模型进行参数识别，并采用其他幅值和频率下的试验数据进行验证.改进后的模型共有17个待识别参数，分别为mi，ni，pi(i=1 ～ 4)，b，α，c0，k0，x0，选取各个电流值下激励振幅为10 mm、频率为0.5 Hz的试验数据进行模型参数识别，电流为0A时识别的参数结果为α=-18.1184，c0=7.7932，k0=4.4664，x0=-28.2211，m1=-4.1981，m2=-0.4860，m3=21.6361，m4=1.4465，n1=-2.5384，n2=-31.67，n3=-5.5477，n4=-15.4476，p1=22.7441，p2=1.75，p3=-7.2675，p4=-76.3833，b=52.1845.同样的方法可以得到其余电流下的参数识别结果. 经分析[26]，对滞回环有显著影响的只有c0，k0，b，α，其余的对滞回环的影响很小，因此可以对其余13个参数取平均值，代入模型，对c0，k0，b，α进行二次参数识别. 然后对得到的识别结果进行曲线拟合，如图6所示.

图6 识别参数拟合曲线. （a） c0；（b） k0；（c） b；（d） αFig.6 Identification parameter fitting curve：(a) c0; (b) k0; (c) b; (d) α

拟合公式为

其中，I是减振器输入电流，A.

用Simulink搭建新型Bouc-Wen改进模型，如图7所示.

在电流为0～2.5 A、激励幅值为10 mm、频率为0.5 Hz的工况下，将Simulink仿真结果与试验所得数据进行对比，如图8（a）所示. 因为模型是以此工况为基础进行识别的，对别的工况（不同激励幅值、频率）是否适用需要进一步的验证，如图8（b）～（f）所示.

图7 Simulink搭建的Bouc-Wen改进模型Fig.7 Bouc-Wen improved model built by Simulink

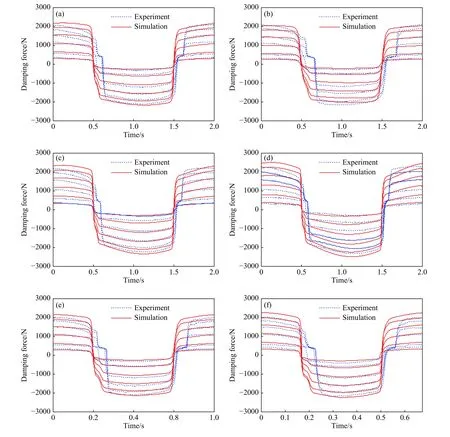
图8 不同工况下的试验值与仿真值时域对比图. （a） 10 mm，0.5 Hz；（b） 5 mm，0.5 Hz；(c) 15 mm，0.5 Hz；（d） 20 mm，0.5 Hz；（e） 5 mm，1.0 Hz；（f） 5 mm，1.5 HzFig.8 Comparison diagram of test value and simulation value under different working conditions: (a) 10 mm, 0.5 Hz; (b) 5 mm, 0.5 Hz; (c) 15 mm,0.5 Hz; (d) 20 mm,0.5 Hz; (e) 5 mm, 1.0 Hz; (f) 5 mm, 1.5 Hz

由图8中各个工况的对比图可以发现，新模型能够较为准确地描述出不同工况下阻尼力的时域特性，无论是识别工况还是非识别工况. 为了更加全面地分析改进模型的滞回特性，下面给出了多种工况下位移与阻尼力的滞回曲线对比情况，如图9所示.

从图9中各个工况的滞回特性对比图中可以发现，无论识别工况图9（a）还是非识别工况图9（b） ～（f），改进的Bouc-Wen模型能够较为准确地描述出不同工况下的阻尼力滞回特性. 图8（a） ～ （d）和图9（a） ～ （d）为相同频率不同激励幅值下的仿真曲线与试验曲线对比情况. 可以看出，除了在识别工况下，在其他非识别工况不同激励幅值下新模型仍然可以准确的描述出阻尼力的滞回特性.仿真曲线没有较大跳跃，即新模型降低了Bouc-Wen模型对非识别工况下幅值的敏感度. 由图8（e）～（f）和图9（e） ～ （f）可知，在相同振幅、不同频率下，仿真值和试验值也吻合的比较准确. 所以阻尼器的试验频率不影响Bouc-Wen模型精度的这一优点在新模型当中得到了继承.

4 模型对比验证

图9 多种工况下的试验与仿真滞回特性对比图. （a）10 mm，0.5 Hz；（b）5 mm，0.5 Hz；（c）15 mm，0.5 Hz；（d）20 mm，0.5 Hz；(e）5 mm，1.0 Hz；（f）5 mm，1.5 HzFig.9 Comparison of hysteretic characteristics between test and simulation under various working conditions: (a) 10 mm, 0.5 Hz; (b) 5 mm, 0.5 Hz;(c) 15 mm, 0.5 Hz; (d) 20 mm, 0.5 Hz; (e) 5 mm, 1.0 Hz; (f) 5 mm, 1.5 Hz

采用文献[12]中的方法对用Simulink搭建好的Bouc-Wen模型进行参数识别和仿真，进而和本文改进的Bouc-Wen模型仿真出来的结果进行对比，从而进一步表明改进模型的优越性和对不同工况的适用性.

4.1 不同幅值和相同频率激励下的模型对比

对比两种模型在不同幅值、相同频率激励下的阻尼力仿真值，分别取幅值为5、10、15、20 mm，频率为0.5 Hz的激励下的仿真值进行对比，如图10所示.

由图10可知，改进后模型的仿真值在各个工况下都较好地吻合了试验值，无论在激励幅值较大还是较小的情况下，都比Bouc-Wen模型吻合效果要好. 在激励幅值为5 mm时，如图10（a）所示，Bouc-Wen模型已经不能够很好地描述滞回环曲线，即Bouc-Wen模型在非识别激励工况下模拟阻尼力精度较差，而改进后的模型依然能较好地模拟滞回环曲线，在激励幅值为20 mm时，Bouc-Wen模型输出的阻尼力过大，而改进的模型改善了输出阻尼力过大这一问题，在非识别工况条件下也具有较强的稳定性，模型的适应能力比之前有了明显的提高，对激励幅值的敏感度有了明显的降低.

图10 不同幅值相同频率的对比图. （a） 5 mm，0.5 Hz；（b） 10 mm，0.5 Hz；（c） 15 mm，0.5 Hz；（d） 20 mm，0.5 HzFig.10 Comparison of fixed frequencies and different amplitudes: (a) 5 mm, 0.5 Hz; (b) 10 mm, 0.5 Hz; (c) 15 mm, 0.5 Hz; (d) 20 mm, 0.5 Hz

4.2 相同幅值和不同频率激励下的模型对比

分别取0.5、1.0、1.5 Hz三种不同激励频率但振幅都为10 mm的工况，对比两种模型在同幅值、不同频率激励下的阻尼力仿真值，如图11所示.

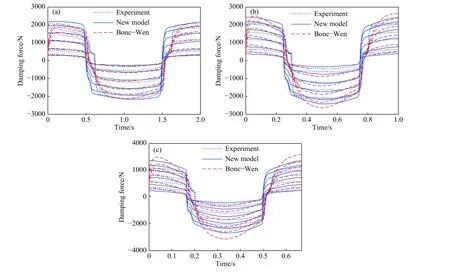
图11 相同幅值不同频率的对比图. （a）10 mm，0.5 Hz；（b）10 mm，1.0 Hz；（c）10 mm，1.5 HzFig.11 Comparison of fixed amplitude and different frequencies: (a) 10 mm, 0.5 Hz; (b) 10 mm, 1.0 Hz; (c) 10 mm, 1.5 Hz

由图11可知，在振幅为10 mm、频率为0.5 Hz的识别激励下，两种模型的仿真滞回曲线与试验滞回曲线吻合效果较好，同时随着激励频率的增大，两种模型输出的阻尼力都与试验值的偏差越来越大. 特别地，在激励频率1.5 Hz下，Bouc-Wen模型输出的阻尼力与试验值有着较大偏差，吻合效果较差，但是改进后的模型能够较好的与试验曲线吻合. 即随着频率的增大，改进模型输出的阻尼力不会与试验值有着较大的偏差，这体现了改进模型具有较强的稳定性.

为了进一步证明改进模型的有效性和优越性，用一种极值误差的方法来对比修正前后模型的阻尼力同试验数据的偏差. 如公式（14）所示.

根据公式（14）计算了修正前后模型在不同工况下的Ferror，如表1所示.

表1 部分工况下改进前与改进后模型的偏差对比Table 1 Comparison of the deviations between the improved model and Bouc-Wen model under some conditions

根据表1可知，改进的模型可以抑制Bouc-Wen模型对非识别激励幅值的敏感度，从而减小偏差. 在不同工况下，改进模型比Bouc-Wen模型在与试验数值对比时偏差均有明显的减小（除个别数值外）. 所以改进的模型解决了Bouc-Wen模型在非识别激励下模拟阻尼力精度差这一缺点，同时还能够平顺且光滑地描述出阻尼器的滞回特性.

5 结论

（1）采用一种利用滞回环斜率与阻尼力的函数关系来描述滞回环形状，即取不同的函数关系即可得到不同的滞回环形状. 根据磁流变阻尼器的滞回环特性，采用了二次多项式函数进行了磁流变减振器的建模. 此方法可以描述多种类型的滞回环形状，具有更为广泛的普适性.

（2）在不同工况下对Bouc-Wen模型进行仿真验证，发现其在非识别工况激励下得到的阻尼力与实际阻尼力误差较大，从而对模型进行改进. 在结论（1）的模型基础上，又在模型中引入一个指数形式的修正项，即速度量，对最终的改进模型进行识别验证，结果表明，新模型增强了对激励振幅的适应性，拟合效果较好，误差有明显减小，新模型在非识别激励工况下取得了较为显著的效果.Bouc-Wen模型在不同激励振幅条件下模拟阻尼力精度较差这一问题在此改进模型中得到了改善.