某航空发动机高压转子连接装配仿真分析*

2020-11-03孙汕民朱林波裴世源

航空制造技术 2020年16期

冯硕，孙汕民，朱林波，裴世源，陈津，周烁

（1. 中国航发沈阳黎明航空发动机有限责任公司，沈阳 110043；2. 西安交通大学化学工程与技术学院，西安 710049；3. 西安交通大学机械工程学院，西安 710049；4. 中国航发上海商用航空发动机制造有限责任公司，上海 201306）

涡扇发动机整机振动问题比较普及，多个型号发动机在科研、批产和服役阶段都长期存在，没有彻底解决，特别是高压转子振动的超限或异常问题，更为突出。高压转子是由高压压气机（HPC）转子和高压涡轮（HPT）转子对接装配而成的组合件，是发动机最为核心的功能部件。高压转子装配制造质量决定了转子结构最终的几何、不平衡和刚度等物理特性，进而直接影响了整机振动响应特征[1–4]。为有效抑制高压转子振动特性，探索、构建高压转子装配过程数据（结构及工艺参数）和转子振动响应之间的复杂规律或关联模型是至关重要的，也是极其困难的。

高压转子装配工艺过程中，HPC/HPT 转子的几何和不平衡测量是比较成熟的，但HPC、HPT 转子对接装配形成高压转子后，处于核心机

单元体状态，高压转子被静子机匣系统覆盖，限于某些型号结构限制所导致的测试或调整成本过高，经济上不可取，一般难以进行动平衡，只能粗略地测量高压转子内腔某一截面的同心度指标[5]。所以，如何根据HPC/HPT 转子的几何和不平衡实测数据以及实际安装相位，进行高压转子的几何和不平衡指标预测，并在此基础上进行振动响应评估是非常重要的。

高压转子装配工艺

高压转子连接装配工艺是指HPC 转子和HPT 转子的对接安装过程，主要工序是螺栓安装、同心度检测。某主机厂采用HPC/HPT 转子以各自测得的SP 位置错开180°进行对接安装，安装完成后采用专用的测量装置分别以高压压气机转子前支点、高压涡轮转子后支点测量篦齿盘盘心位置的跳动，检查两个转子装配后的组合转子同心度是否在要求的范围内。经过上述方法装配完成后，大多数转子盘心跳动能保证在合格范围内，但由于缺少预测方法，仍有跳动超差的情况发生。同时由于某些型号发动机高压压气机、高压涡轮转子是单独平衡，装配完成后的组合转子受结构限制，测试或调整成本过高，一般在传动装配后不进行动平衡测量检查，导致转子在组合状态下的动不平衡量难以预测。

高压组合转子装配性能建模技术方法

1 高压组合转子刚性堆叠技术原理

假设高压转子安装边止口配合由最小二乘中心及最小二乘平面同时重合完成，则数学上止口配合可用两个配合面的齐次坐标变换矩阵相等来实现[6–8]。两级盘进行配合时，以下层盘的底面为测量基准，配合面，装配完成后上层盘上止口的空间位姿如图1 所示，可由以下方程计算得到

图1 零件之间误差传递示意图Fig.1 Schematic diagram of error transmission between parts

若安装边止口的z 向坐标为h，不计其高度误差，xc、yc为止口拟合圆心坐标，(–A，–B，1)为止口端面朝正方向的单位法向量，通过先平移再转动的方法，可以获得安装边止口在测量坐标系中的齐次坐标矩阵。

如果是多级盘，以最底部盘的底面为基准，那么第i 级盘上止口的空间位姿可由以下方程求解得到

2 考虑装配误差的零件不平衡量计算

零件自身的不平衡量是由于制造误差、材料不均匀等引起的零件相对基准轴线（由装配连接面确定）的不平衡量，该不平衡量可通过平衡机进行测量。若零件在工作状态下绕其基准轴线旋转，则零件自身的不平衡量即为其最终不平衡量。然而由于多级零件的组合装配，零件基准轴线会偏离转子的回转轴线，产生偏心误差，从而造成零件不平衡量的变化[9–10]。

零件基准轴线偏离转子回转轴线有两种表现形式：第一，纯径向偏离，即轴线平行但不重合，这种情况下会产生不平衡力；第二，纯角度偏离，即转子的惯性轴与基准轴线相交于质心位置，这种情况下会增加零件的不平衡力矩。实际中，这两种形式通常同时存在，零件的不平衡力和不平衡力矩均会受到影响。对轴线偏离造成的不平衡量进行求解，进而与零件自身的不平衡量进行矢量组合即可得到零件在工作状态下的不平衡量。

本文利用达朗贝尔原理计算零件的惯性力和惯性力矩，借鉴刚体绕非惯性主轴转动时不平衡力偶计算方法[11]，求解由于装配误差（偏心和倾斜）造成的两个平衡面上的不平衡量mr12和mr22。零件自身的不平衡量以及由于轴线偏离造成的不平衡量通过矢量相加即可得到两个平衡面上的最终不平衡量。此处的mr11和mr21是根据零件自身不平衡量以及零件的装配角度求解得到的。

组合转子在前后轴颈位置处以轴承进行支撑，因此回转轴线是由两个轴颈确定的。在计算装配误差时，以回转轴线为Z 轴，零件的最底面作为XOY 平面建立全局坐标系。通过误差传递分析求得每个零件装配连接面的中心坐标，以此可用几何方法得到零件质心的坐标以及基准轴线的角度误差。

求得每个零件平衡面上的不平衡量后，按照在转子中的装配位置关系依次排列，如图2 所示。以平衡面A 的中心为基准，各平衡面上的不平衡量存在以下关系

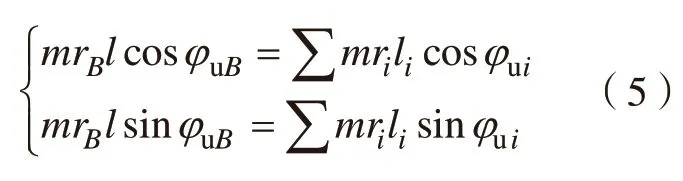
据此可以求得平衡面B 上的等效不平衡量。同理以平衡面B 的中心为基准，可以求得平衡面A 上的等效不平衡量。两者的矢量和为转子整体的静不平衡量。

3 高压转子动力学建模

当转子高速旋转时，由于不平衡载荷的激励作用，将会发生变形、振动等动态响应。对旋转机械的动态性能进行分析可以定量评估装配误差对系统动态服役性能的影响。不平衡载荷为纯径向力，且两个方向上的分量是正弦变化的力，将其作为时变激励代入轴承转子动力学分析模型，就可以求得转子在不平衡量下的响应，识别旋转机械各处的振动情况，同时也可以对轴承的附加动反力进行考察。

以Timoshenko 梁单元和弹簧单元建立发动机高压转子的有限元分析模型，整个系统的动力学方程为：

其中，[M]为系统的质量矩阵；[C]为系统的结构阻尼矩阵；[G]为陀螺矩阵；[K]为系统的刚度矩阵；[B]为旋转阻尼矩阵；为系统的加速度向量、速度向量以及位移向量；{F}为系统的载荷向量。

将两个平衡面处的不平衡力代入{F}中，对方程进行求解，即可分别从位移向量和载荷向量中提取各处的振动幅值和轴承的附加动反力。

以某型发动机高压组合转子为例，本文利用自行研发的转子动力学分析软件，建立了高压转子动力学仿真分析模型，如图3 所示，该模型主要由梁单元组成，高压压气机前轴和高压涡轮后轴分别设置弹簧单元模拟支撑轴承，在4 个节点位置分别施加高压压气机转子两个平衡面和高压涡轮两个平衡面的初始不平衡量。

图2 组合转子不平衡量合成示意图Fig.2 Synthetic diagram of rotors unbalance combination

图3 高压转子动力学仿真分析模型Fig.3 High-pressure rotor dynamics FE model

结果与讨论

本文以所建立的高压转子动力学仿真模型为基础，对比现有航空发动机制造企业常见的高低点匹配、轻重点匹配和SP 值匹配3 种高压组合转子装配方法，分析不同装配方法对高压组合转子动力学特性的影响规律；利用遍历法分析不同高压涡轮装配相位下各平衡面不平衡量和动力学响应特性的变化规律，寻找最佳装配相位；以此为基础，分析高压压气机篦齿盘端面和高压涡轮后轴颈端面跳动幅值与初始不平衡量对转子动力学特性的影响。为了对比分析，本文参考航空发动机实际装配结构与工艺参数，设计了5 种装配工况与案例，如表 1 所示。表 1 中高压压气机HPC 跳动检测位置在篦齿盘处，高压涡轮HPT 跳动检测位置在后轴轴颈处。

1 高压组合转子3 种装配方法对比

现有航空发动机制造企业常见的高压组合转子装配方法主要有3种。（1）高低点匹配方法，即通过精密转台检测高压压气机转子篦齿盘端面与高压涡轮转子后轴轴颈端面的高点和相位，以相位差180°为装配相位进行安装；（2）轻重点匹配方法，即通过平衡机分别检测高压压气机转子和高压涡轮转子两个平衡面的初始不平衡量和相位，计算每个组件初始不平衡量矢量和，进而依据相位差180°为装配相位进行安装；（3）SP 值匹配方法，即通过精密转台检测高压压气机转子篦齿盘端面与高压涡轮转子后轴轴颈端面的SP 值和相位，以相位差180°为装配相位进行安装。

本文以表 1 中装配工况2 为案例，利用提出的刚性堆叠算法，分别计算高低点匹配、轻重点匹配和SP值匹配相对前后轴颈联合基准的装配误差，以此为基础，求解由装配误差引起的高压压气机转子和高压涡轮转子两个平衡面的二次不平衡量，从而将各平衡面的二次不平衡量与初始不平衡量矢量和施加于本文建立的高压转子动力学仿真模型之中。通过计算可得，高低点匹配、轻重点匹配和SP 值匹配3 种装配方法的装配相位分别为10°、183°和77°。

表1 高压转子装配工况Table 1 High-pressure rotor assembly cases

图4～6 分别为高压转子装配工况2 下3 种装配方法的高压转子组件前后轴承轴颈不平衡量响应幅值和相位，图 7 为高压转子装配工况2 下3 种装配方法的前后轴承轴颈不平衡量响应幅值对比结果。由图4～6 可以看出，在工作转速内，当转速达到6633r/min 时，前后轴承位置会产生较大振动。由图 7 可以看出，高低点匹配装配方法不平衡量响应幅值最小，其次为SP 值匹配方法，轻重点匹配方法最大。因此，如果以不平衡量响应特性为评价标准，针对高压转子装配工况2，3 种装配方法中高低点匹配装配方法最优，其次为SP 值匹配方法，轻重点匹配方法最差。

2 高压组合转子装配相位对动力学影响分析

同样，以表1 中装配工况2 为案例，利用提出的刚性堆叠算法和装配误差等效方法，分别计算不同装配相位下各平衡面的二次不平衡量与初始不平衡量矢量和，进而分析装配相位对不平衡响应的影响规律。

图4 高低点匹配方法下高压转子前后轴承不平衡响应特性Fig.4 Unbalance response characteristics of front and rear bearing for high-pressure rotor under high and low point matching assembly method

图5 轻重点匹配方法下高压转子前后轴承不平衡响应特性Fig.5 Unbalance response characteristics of front and rear bearing for high-pressure rotor under unbalance matching assembly method

图8 为高压转子装配工况2 下高压组合转子4 个平衡面不平衡量随安装相位变化的关系曲线。可见，4 个平衡面不平衡量随着安装相位的变化呈非线性变化，出现该现象的主要原因为不同安装相位造成不同装配误差，由此引发的二次不平衡量也随之发生变化，从而导致各平衡面初始不平衡量与二次不平衡量矢量和呈现非线性特性。图9、10 分别为高压转子装配工况2 不同转速情况下前后轴承不平衡量响应幅值随安装相位变化的关系曲线。可以看出，随着装配相位的变化，高压组合转子前后轴承不平衡量响应幅值发生明显变化，且存在最优装配相位。同时发现，针对高压转子装配工况2，在不同转速状态下高低点匹配装配方法的前后轴承轴颈处不平衡量响应幅值始终小于轻重点匹配方法和SP值匹配方法，而轻重点匹配较其他两种装配方法响应幅值最大，但值得指出的是3 种装配方法并非最优装配相位。此外，在装配相位变化过程中，后轴轴颈承受的不平衡量响应幅值较前轴承更大，这主要是由于本文选择的航空发动机高压转子组件装配工况中高压涡轮转子初始不平衡量大于高压压气机转子。

图6 SP值匹配方法下高压转子前后轴承不平衡响应特性Fig.6 Unbalance response characteristics of front and rear bearing for high-pressure rotor under SP matching assembly method

图7 3种装配方法下高压转子前后轴承响应幅值对比Fig.7 Unbalance response characteristics of front and rear bearing for high-pressure rotor under three matching assembly methods

图8 安装相位与各平衡面不平衡量关系曲线Fig.8 Relationship between installation phase and unbalance of each balance plane

3 端面跳动对动力学影响分析

为了分析端面跳动幅值对高压组合转子动力学特性的影响，本文以表1 中装配工况1～3为案例，分别选取高压压气机转子篦齿盘端面和高压涡轮转子后轴轴颈端面0.01mm、0.02mm 和0.03mm 的跳动幅值，并系统对比3 种装配方法在不同端面跳动幅值下的动力学表现。图 11 为不同端面跳动幅值下前后轴承轴颈不平衡量响应幅值的变化曲线。可见，端面跳动幅值越大，高压转子不平衡量响应幅值越大，高低点匹配装配方法下振动响应幅值整体小于轻重点匹配和SP 值匹配，但随着端面跳动幅值增大，3 种装配方法的动力学表现差距逐渐减小。

4 初始不平衡量对动力学影响分析

为了分析初始不平衡量对高压组合转子动力学特性的影响，本文以表 1 中装配工况2、4 和5 为案例，分别选取高压涡轮转子两个平衡面初始不平衡量为（300g·mm，500g·mm），（500g·mm，1000g·mm）和（1000g·mm，1500g·mm），并系统对比3 种装配方法在不同初始不平衡量下的动力学表现。图 12 为不同高压涡轮转子初始不平衡量对前后轴承不平衡响应幅值的影响曲线。由图 12 可以看出，随着高压涡轮初始不平衡量的增大，转子后轴轴承不平衡量响应幅值逐渐增大，但影响程度小于端面跳动幅值，且发现SP 值匹配方法对初始不平衡量比较敏感，初始不平衡量越大，SP 值匹配装配方法的动力学表现越差；同时发现，在小于临界转速情况下，3 种装配方法对振动响应幅值影响有限，但随着转速升高，高低点匹配下振动响应幅值明显小于另外两种装配方法。

图9 安装相位与前轴承不平衡响应幅值关系曲线Fig.9 Relationship between installation phase and unbalanced response amplitude of front bearing

图 10 安装相位与后轴承不平衡响应幅值关系曲线Fig.10 Relationship between installation phase and unbalanced response amplitude of rear bearing

图11 端面跳动幅值与前后轴承不平衡响应幅值的关系曲线Fig.11 Relationship between flat face runout amplitude and unbalanced response amplitude of front and rear bearings

结论

（1）建立了高压组合转子刚性堆叠计算模型，提出了考虑装配误差的零件不平衡量计算方法，实现了装配误差在各平衡面上的不平衡量等效；以此为基础，构建了高压组合转子动力学仿真分析模型。

（2）以高压转子某一装配工况为例，对比了航空发动机制造企业常见的高压组合转子装配方法，发现以不平衡量响应特性为评价标准，3 种装配方法中高低点匹配方法最优，其次为SP 值匹配方法，轻重点匹配方法最差。

（3）以高压转子某一装配工况为例，分析了装配相位对不平衡响应特性的影响规律，发现随着装配相位的变化，高压组合转子前后轴承轴颈不平衡响应幅值发生明显变化，且存在最优装配相位，而现有常见的3 种装配方法并非最优装配相位。

（4）针对不同高压转子装配工况，分析了端面跳动与初始不平衡量对高压组合转子不平衡响应特性的影响规律，发现端面跳动幅值越大，高压转子不平衡响应幅值越大；初始不平衡量增大，高压转子后轴轴承不平衡量响应幅值逐渐增大，且发现SP 值匹配方法对初始不平衡量比较敏感，初始不平衡量越大，SP 值匹配装配方法的动力学表现越差。

（5）由研究结论可见，航空发动机高压组合转子，特别是大跨度多级盘轴高压组合转子结构，在实际装配过程中应优先采用高低点匹配装配方法，有条件的情况下可对装配相位进行优化设计，且要严格控制高压压气机篦齿盘端面跳动幅值，从而保障高压组合转子的动力学特性。后续将开展更多装配工况分析工作，验证本文结论的普适性。