拖曳式诱饵弹落差评估方法研究

周 健, 欧 平, 刘 森, 张 江, 魏 巍, 秦永明

(中国航天空气动力技术研究院, 北京 100074)

0 引 言

随着制导技术的迅速发展，导弹所显示出的威力日益增大，为保护载机飞行器免于导弹攻击，拖曳式诱饵弹作为可重复使用干扰装置可以极大地提高飞行器的反导弹生存能力，在关键时刻能够“牺牲”自我而保护载机的安全，国外军事大国已经竞相将此作为现代电子战防御系统中不可或缺的一部分[1-4]。拖曳式诱饵弹的具体实现方式为：当载机飞行器(多为飞机或巡航弹)遭受导弹攻击时，通过拖曳线缆将诱饵弹迅速释放并拖曳飞行(如图1所示)，诱饵弹发射出强功率干扰信号诱导导弹的攻击偏离载机，若任务结束或危险过去后诱饵弹未被损坏，再通过拖曳线缆将诱饵弹收回以供重复使用[5]。在未受导弹攻击时，诱饵弹藏于飞行器腹仓内，不影响飞行器的飞行气动性能。

为保护载机完全避免攻击，拖曳线长度需要大于攻击导弹的破坏半径，一般在几十米到上百米量级。由于诱饵弹存在一定质量，投放后稳定拖曳时会与载机存在一定落差，当飞行器掠海或超低空飞行时需保证飞行高度大于诱饵弹拖曳落差，否则一旦诱饵弹落进海中或与地面相碰，就有可能导致惨烈的后果。因此，对拖曳式诱饵弹落差的准确评估成为其设计定型中不可缺少的研究部分。国内外对拖曳式诱饵弹落差的研究多以绳索动力学为基础，从释放过程开始研究诱饵弹弹体和拖曳绳索的动力学特性。Zhu等[6]用解析方法对稳定飞行状态下的载机系统进行研究，得到了拖曳系统的解析解；Kolodner[7]和Wu[8]分析了无空气阻力情况下拖曳绳索的非线性运动，提出了渐近解方法；Quisenberry[9]通过低空拖曳对海平面的波动问题进行了研究，采用有限差分法建立了缆绳的三维仿真模型，重点分析了系统的动力学问题和控制的稳定性；Williams等[10-12]研究了空中拖曳系统在运动中绳索的变形以及拖曳物体的运动轨迹问题，并进一步分析了不同拖曳点对拖曳稳定性的影响。国内马东立等[13]将柔性拖曳缆绳离散为一系列由阻尼弹簧连接的节点，建立了缆绳的动态模型，并分析了缆绳的形状、张力和诱饵的姿态角等参数的变化规律。由于绳索具有无限的自由度，考虑非线性因素的作用时，整个过程呈现出复杂多变的动力学特性，常规建立数学物理模型的研究方法多为动力学规律性研究，而不以模拟诱饵弹最终拖曳落差为目的。

图1 诱饵弹拖曳飞行

本文以某掠海飞行器拖曳式诱饵弹1∶1试验模型为研究对象，首先通过风洞拖曳试验对不同构型诱饵弹的拖曳状态及落差情况进行分析研究，获得该构型诱饵弹的拖曳特性。然后分析诱饵弹稳定拖曳状态下的受力情况，建立基于诱饵弹气动特性的落差计算手段。最后针对工程实践问题给出拖曳式诱饵弹的优化设计与落差评估方法。

1 风洞拖曳试验

1.1 试验设备与装置

试验在中国航天空气动力技术研究院的FD-12风洞进行。该风洞是一座直流暂冲式亚跨超三声速风洞，试验段截面尺寸为1.2 m×1.2 m，马赫数范围为0.3～4.0，跨声速试验段长度为3.8 m。

试验段两侧壁各有2个观察窗，用于观察和录摄诱饵弹拖曳姿态，利用现有侧窗平台设计加工拖曳放线机构，如图2所示。支架前缘整流锥出线孔位于风洞中轴线，诱饵弹拖曳线通过支架走线槽以及滑轮与放线卷轴连接，由电机驱动卷轴实现收放线。

图2 拖曳机构简图与照片

1.2 试验模型

试验模型为某掠海飞行器拖曳式诱饵弹原尺寸模型，外形有平头和斜头2种，模型简图见图3。斜头构型设计目的为与载机飞行器表面保型。拖曳线由诱饵弹头部引出，尾部为一环形安定翼，试验模型可通过内部配重块调节质心位置。拖曳线为诱饵弹专用拖曳线缆，密度为5 g/m，直径为1.5 mm。

图3 诱饵弹试验模型简图

为模拟真实飞行时的拖曳状态，诱饵弹试验模型除需满足几何相似条件外，质心位置还需与实物一致；同时，由于风洞吹风动压与真实飞行条件不同，试验模型质量与实物还需满足一定的关系。下文将对风洞拖曳试验所需满足的相似准则作具体说明。

1.3 试验方法

本试验利用高速摄像获得诱饵弹的拖曳状态，主要包括稳定拖曳时的模型迎角α及拖曳线与来流夹角φ(下文简称拖曳线夹角)，通过拖曳线夹角φ和真实放线长度l计算得到诱饵弹拖曳落差h=lsinφ。高速摄像采样频率100 Hz，分辨率1280 pixel×1020 pixel。

试验前先对诱饵弹模型拖曳位置(观察窗处风洞纵向对称面)坐标进行标定。风洞流场建立后，缓慢放线使试验模型到达观察窗摄像位置,进行拖曳状态拍摄，并通过图像合成分析获得诱饵弹模型的拖曳姿态信息，如图4所示。由于稳定拖曳状态下试验模型也存在微小的摆动，故需分别取摆动的上下边界图像进行处理分析。

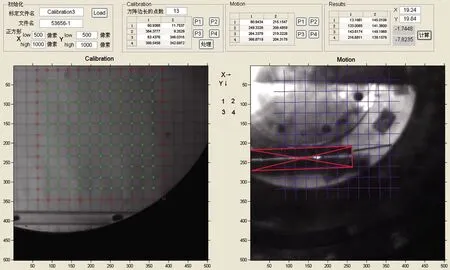
图4 图像分析处理软件

1.4 试验结果与分析

对2种试验模型各3个质心位置进行拖曳放线试验，风洞来流马赫数Ma=0.7，总压p0=113 400 Pa，总温T0=296 K，单位雷诺数Re=1.4×107/m。

试验结果发现斜头构型3个质心位置均未出现稳定拖曳状态，放线过程中模型一直作无规律大幅度摆动，甚至出现与支架碰撞的现象。分析其可能的原因为斜头构型头部直径大于等直段，流动经头部后出现非定常涡脱落现象，使得安定翼附近流场紊乱，模型受扰动后回稳效率下降。

平头构型具体拖曳姿态如表1所示，其中质心参考原点为诱饵弹轴线与头部端面交点，参考长度为诱饵弹全长。可见，该诱饵弹构型在质心最靠前状态出现拖曳失稳现象，常规“质心越靠前静稳定裕度越高”的认识不适用于拖曳式飞行器。分析其可能的原因为：诱饵弹受扰动回稳过程中，姿态角的变化不仅引起其本身气动特性的改变，还使得拖曳线作用到诱饵弹上的力/力矩发生改变，两者的相互耦合决定最终拖曳状态。通过稳定拖曳状态下诱饵弹姿态可知：在小幅摆动过程中，模型最大迎角α对应最小φ角状态，最小迎角α对应最大φ角状态，这也是诱饵弹静稳定特性的表现；模型稳定拖曳状态下迎角α随质心的后移整体呈增大趋势，同时拖曳线夹角φ的波动范围变大，分析其可能的原因为稳定拖曳状态下模型质心的后移导致其静稳定裕度下降。

表1 平头构型拖曳姿态信息Table 1 Towed attitude of flat head configuration

2 风洞测力试验

风洞拖曳试验虽然可以模拟诱饵弹真实飞行条件下的拖曳姿态，包括拖曳稳定性和落差等，但其试验成本较高，机构复杂，一旦出现拖曳不稳定或拖曳线断开现象，就很有可能对风洞壁和观察窗带来损坏，存在较大的未知风险。本节从诱饵弹受力分析入手，利用风洞测力试验开展拖曳式诱饵弹落差评估方法研究。

2.1 研究思路与方法

由于风洞来流雷诺数与实际飞行条件相差不大，可以认为风洞条件下诱饵弹气动力与力矩系数与真实飞行条件下一致。真实拖曳稳定状态下诱饵弹受力情况如图5所示，此时诱饵弹受拖曳线拉力、气动力和重力作用，根据力与力矩平衡可得如下关系式：

力平衡：

L(α)+Fy=mg，D(α)=Fx

(1)

力矩平衡：

Ma(α)=mg·A(α)

(2)

其中,L(α)为诱饵弹气动升力，D(α)为诱饵弹气动阻力，Ma(α)为诱饵弹关于拖曳点的俯仰力矩，A(α)为诱饵弹重力对拖曳点的力臂，此几项均与诱饵弹当前迎角α(诱铒弹轴线与来流的夹角)有关；Fx和Fy为拖曳线拉力F沿阻力方向和升力方向的分力；诱饵弹重力mg、拖曳点和质心位置坐标均为已知量。通过风洞测力试验可获得诱饵弹模型随迎角变化的升力系数CL(α)，阻力系数CD(α)和相对诱饵弹拖曳点的俯仰力矩系数Cma(α)，进行函数拟合后,结合上述3个方程式，可解得真实拖曳状态下拖曳线夹角φ的表达式如下：

图5 拖曳稳定状态下诱饵弹受力情况

(3)

其中，Q为真实飞行动压，Sr为参考面积，α0为诱饵弹拖曳稳定状态下的迎角，可由式(2)获得其数值解。φ是拖曳点位置拖曳线与来流的夹角，该值理论上与拖曳线无关，而真实情况下拖曳线由于受自身重力、气动力的作用，当长度较大时，整体是存在弯曲变形的，但曲率较小，进行落差估算时可近似视为直线[14]。

除此之外，由φ的表达式可知，若要通过风洞拖曳试验获得诱饵弹真实拖曳落差，试验模型的几何外形、质心位置和质量均需满足动力相似。几何相似保证气动特性一致，质心位置相似保证α0值相等，质量则需满足下式：

(4)

2.2 试验模型

针对拖曳稳定状态的平头构型，设计加工1∶1风洞测力试验模型，在与拖曳试验同一来流参数下开展测力试验。试验采用尾支撑方式，为最大程度模拟诱饵弹尾部流场，在保证模型不碰到支杆的条件下设计加工尾部堵盖，并沿周向不同位置进行压力测量，以监测尾部流场情况，如图6所示。

图6 诱饵弹测力模型装配剖视图

2.3 试验结果与分析

由风洞拖曳试验可知，平头构型稳定拖曳时模型迎角均小于3°，据此测力试验迎角范围定为-3°～3°，得到升力系数CL、阻力系数CD以及关于拖曳点的俯仰力矩系数Cma如图7所示。

对试验所得各气动系数点进行多项式拟合，得到各气动系数关于迎角α的关系式如下：

升力系数：CL(α)=0.0388α-0.0552

阻力系数：CD(α)=0.0033α2-0.0037α+0.9944

关于拖曳点的俯仰力矩系数：

Cma(α)=0.0004α3-0.0006α2-0.0261α+0.0357

利用上述函数表达式，根据2.1节所述稳定拖曳时模型迎角α和拖曳线夹角φ的表达式，计算得到平头构型受力平衡状态下的拖曳姿态如表2所示。通过对比可知，计算所得拖曳稳定时诱饵弹姿态角与拖曳试验存在一定差异，质心32.3%构型模型稳定迎角α在拖曳试验模型摆动范围内，但拖曳线夹角φ比拖曳试验大1°左右；质心34.3%构型拖曳线夹角φ在拖曳试验摆动范围内，模型稳定迎角α比拖曳试验大0.2°左右。可见，在一定误差带范围内，可以通过测力试验模拟诱饵弹稳定拖曳时的姿态。造成两者差异的主要误差源为流场误差、模型误差和测量误差3种，其中流场误差主要表现在拖曳试验支架和拖曳线对下游模型流场的干扰，模型误差主要为尾支撑方式对模型尾部流场的干扰，测量误差为整个天平测控系统的测量误差。

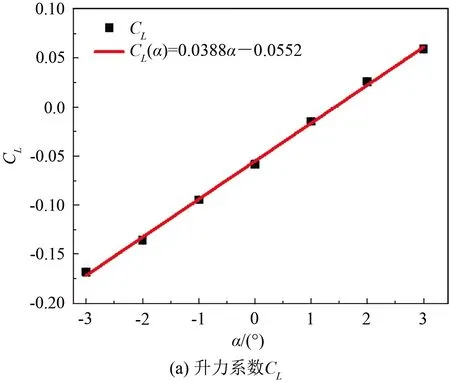
图7 诱饵弹气动特性曲线

表2 拖曳姿态计算结果Table 2 Computed results of towed attitude

综上所述，通过测力试验获得的稳定拖曳姿态为单点稳定状态，包括静稳定点和静不稳定点。但通过该方法无法确定诱饵弹构型是否可稳定拖曳，也无法获得稳定拖曳状态下的动稳定区间，这是该方法的不足之处。

3 应用方法研究

由2.1节可知，诱饵弹特定飞行状态下的拖曳落差由其气动外形、质量、质心位置和拖曳点位置4个因素确定，其中气动外形决定了诱饵弹的气动特性。对于常规飞行器(诱饵弹)构型，小迎角范围内升力系数为迎角的一次函数，阻力系数为迎角的二次函数。由稳定拖曳状态下φ的表达式可知，在不考虑力矩平衡的前提下，φ为稳定拖曳迎角α的单调函数，且随α的增大而减小，图8为本文诱饵弹外形下φ-α关系曲线。结合式(2)可知，通过改变质量、质心位置或拖曳点位置均可得到诱饵弹稳定拖曳状态下的迎角α0，进而利用φ-α关系式便可获得满足落差要求的诱饵弹构型特性。

图8 稳定拖曳时φ随α的变化曲线

综上所述，对各影响因素均已确定的诱饵弹落差评估可直接进行风洞拖曳试验，对其拖曳落差、静稳定和动稳定特性进行考核。除此之外，对以最小落差为目标的诱饵弹优化选型，则可通过调整上述4个影响因素获得，由于气动外形、质量和质心位置3者为相互耦合关系，很难单独对某一方面进行调整，加上内外结构的约束，可调能力有限，而拖曳点位置的改变基本不会引起其他3个因素的变化。据此，以拖曳点位置为单变量开展诱饵弹拖曳落差的优化研究在工程应用中简单可行，总体的思路为：首先以风洞测力试验(或数值模拟)为先导，把握诱饵弹拖曳状态下的气动特性，进而获得不同拖曳点位置对拖曳落差的作用规律，择出满足拖曳落差要求的典型状态进行风洞拖曳试验验证并考核其动态特性。

4 结 论

本文针对真实飞行条件下拖曳式诱饵弹的落差评估问题，开展基于风洞拖曳试验与测力试验的系统性研究，主要得到以下结论：

(1) 对于拖曳式诱饵弹，头部外形对拖曳稳定性影响较大；同时在拖曳线拉力和气动力共同作用下，并非质心越靠前静稳定性越高，两者的相互耦合决定最终拖曳状态。

(2) 在稳定拖曳前提下，通过风洞测力试验获得诱饵弹气动参数曲线，结合受力平衡方程和诱饵弹相应参数可解算得到诱饵弹的稳定拖曳姿态，通过对比分析，验证了该方法的可行性。

(3) 通过深入分析稳定拖曳状态下诱饵弹的气动特性，结合2种试验的优缺点，给出工程实践中拖曳式诱饵弹的优化设计与落差评估方法。

此外，本文研究内容以风洞试验为平台，其中风洞拖曳试验放线长度约2 m左右，对于落差评估方法的研究结论基于拖曳线缆伸长不变形的假设，这也使本文研究不可避免地存在一些不足之处。