某轻型物流车的实时车载称重系统方案

于法祥，苗少光

(1.北汽(常州)汽车有限公司，江苏 常州 213001； 2.深圳市汉德网络科技有限公司，广东 深圳 518000)

目前物流运输车主要使用地磅进行称重，由于缺乏有效的实时称重手段，物流运输行业乱象丛生，超载等违规现象屡禁不止[1-3]。随着物流运输行业的快速发展，需要实时称重的场景越来越多，要求也越来越高。此外，为了规范物流运输行业健康有序发展，国家也已发布多项标准法规[4]，现有的地磅称重方案已不满足需求。为解决上述问题，本文介绍一种实时车载称重系统方案[5]。

1 初始方案设计及其可行性

1.1 初始方案设计

初始方案总体设计与力传感器布置如图1所示。其中传感器1～N安装在前桥及后桥半轴受力位置，实时感应安装点的重力数据；主控终端用于采集和预处理力传感器数据并上传到云平台(主控终端内集成通讯模块，安装SIM卡后即可与云平台通讯)；云平台用于将上传的力数据进行分析、计算，并通过已拟合出的重量计算公式得出所称重数据，然后回传给主控终端；监控系统用于远程监控，通过专用网站显示云平台计算结果，实现对车辆载货情况实时监测；显示器用于汽车装载量实车显示[6-7]。

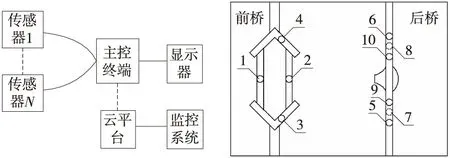
图1 方案总体设计及传感器布置

从设计方案看，关键点在于传感器安装点的选择。要考虑所选安装点的受力线性、安全性、前期安装和后期维护便捷性等。

1.2 初始方案可行性测试

选择一辆如图1所示的标准配置样车作为测试对象，后桥半轴类型为方形。

1.2.1 标准载货方案设计及测试

该车型设计标准装载量为0～1 500 kg，实测范围0～1 533 kg。测试过程中所用载重约为20 kg/桶的沙桶，通过不断地加载与卸载，同步观测对比力传感器数据，拟合出一个重量计算公式。拟合方法如下：

Y=a×X1+b×X2+c×X3+d×X4+e×X5+f×X6+C

(1)

式中：Y为系统输出的重量值，即监控平台和车载设备显示的装载重量；X1为力传感器直接测量数据，即传感器依据形变计算的载重数据；a为根据传感器安装位置的形变难易程度进行调整的权重系数，使传感器数据保持在一定范围内；X2为车辆运行状态修正值，即车辆运行和静止两种状态下的补偿数据；b为运行与静止状态调整权重系数，平衡该状态因素对力传感器直接测量数据的影响；X3为装卸货状态修正值，即车辆加载和卸载两种状态下的补偿数据；c为加载和卸载状态调整权重系数，平衡该状态因素对传感器测量数据的影响；X4为气压值修正值，即不同大气压下的补偿数据；d为环境气压调整权重系数，补偿气压因素对测量数据的影响；X5为温度值修正值，即不同温度下的补偿数据；e为环境温度调整权重系数，补偿温度因素对测量数据的影响；X6为其他因素修正值，即其他影响因素的补偿数据；f为其他因素权重系数；C为可调整常数，对最终输出结果Y进行总体修正。

得到基本公式(1)后，加入跑车工况测试并持续对该公式进行改进。首轮共进行15组加载试验(静态测试9组，跑车测试6组)，该阶段由于时间较为充裕，公式改进只采用上货过程(与实际载物场景类似)的数据。公式(1)的优化过程见表1。

表1 公式(1)的优化过程

此处引用静态第九次加载试验数据对静态方案可行性进行分析，引用动态第二次加载试验数据对动态方案可行性进行分析，衡量标准为称重误差[8]。

称重误差计算公式如下：

称重误差=|Y-实际重量|/实际重量

(2)

称重误差曲线如图2所示，公式(2)中的Y采用表1中的Y2。

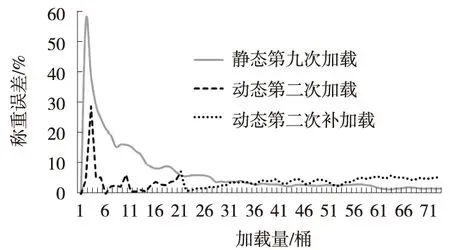
图2 加载量误差曲线图

1) 静态可行性分析。从图2可以看出，随着加载量的增加，静态误差不断下降并最终趋于稳定。说明该方案在该车型上不仅理论上可行，技术实现上也可行。对比另外8组静态测试数据，除首组标定用数据外，其余7组数据总体效果基本相同。

2) 动态可行性分析。从图2可以看出，随着加载量的增加，动态误差逐渐趋于稳定。对比另外5组跑车测试数据，总体上效果一致。

下面重点针对动态方案的可靠性进行验证。

3) 最终组数据分析。将总第15组即动态第六次加载试验数据进行分析。该组试验共计两个阶段：第一阶段(公式Y4)加载测试，其测试结果在后半部分误差较大。结合这第一阶段新的称重数据，对公式进行改进升级为Y5，再进行第二阶段加载测试，测试结果误差明显降低。其加载误差曲线如图3所示，图中动态测试第六次数据第二阶段与第一阶段相比，改进后的称重计算公式Y5精度有明显提升，且更为稳定。

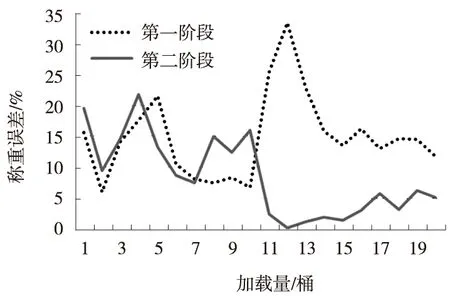
图3 最终组数据误差-加载量曲线图

4) 不同传感器数量方案对比。整车标准配置为10个传感器，为后期降本考虑，下面适当减少传感器，分析不同数量传感器方案的精度。6个传感器方案：选用图1中的2、3、4、6、9、10号传感器；4个传感器方案：选用图1中的2、6、8、9号传感器。

对比汇总测试结果见表2，选择称重值误差10%作为标准，并以此标准得到不同传感器数量方案的达标率(即达到10%称重误差的数据比率)进行效果对比，公式选择Y5。

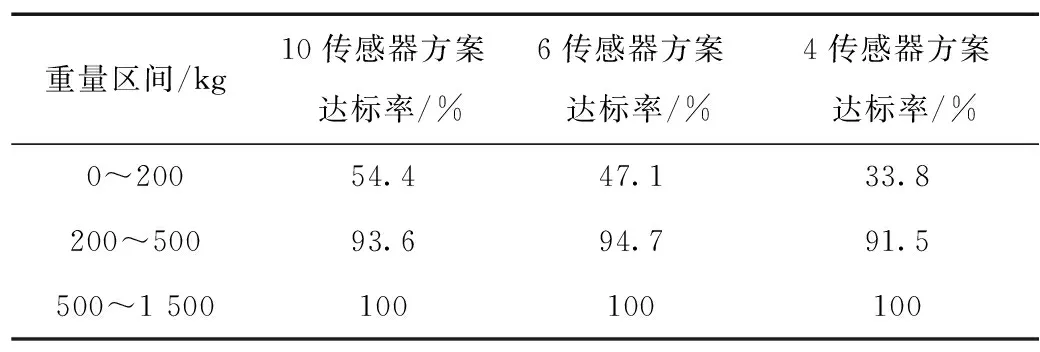
表2 不同传感器数量标载测试达标率对比

从表2可看出，传感器数量对称重精度有一定影响。但随着加载量增加，当超过500 kg时，3 种方案的达标率都为100%，误差都保持在10%以内，满足使用要求。所以，在后续方案选择上，可根据实际需要，选择合适数量传感器方案，达到需求和成本的最优选。

1.2.2 超载方案设计及测试

超载方案测试过程中，由于采用人工加卸载，劳动量过大，考虑到时间周期也较为紧张，因此将卸载数据也进行充分利用。即超载方案按照上货过程和下货过程两个场景联合测试，参考公式Y5。

1) 上货过程。传感器安装点同图1。目标超载测试范围1 500～3 000 kg，实测范围1 000～3 015 kg，共计进行3个循环的上下货测试。

参照前面1.2.1中4)方案，分别选择10%、20%、30% 3种称重值误差作为标准，测试不同传感器数量方案在3种误差标准下的达标率。得到测试结果见表3。

表3 上货过程超载测试达标率对比

2) 下货过程。参照前面1.2.1中4)方案，误差值标准同1.2.2中1)中的上货过程，分析不同传感器数量方案，得到测试结果见表4。

表4 下货过程超载测试达标率对比

对比以上数据，发现同样数量传感器，在上、下货状态下系统的最大误差完全相同，系统稳定性较好。此外，无论是上货过程，还是下货过程，随着传感器数量下降，误差变大，一致性明显，同此前测试结论相同。总体上，该方案超载试验结果符合设计预期。

1.2.3 精确称重范围确定

测试范围0～400 kg。方案测试过程中，考虑到快递行业揽件过程中，需要即时精准称重。所以，在完成以上标载及超载测试内容后，在靠近货箱尾门居中选择60 cm×80 cm区域，作为模拟揽件称重区域。经调试，在该区域可实现误差低于3%，绝对误差低于2 kg。

该功能的安装及调试要求较高，无法实现标准化搭载，不作为本文重点讨论内容，不做过多描述。

1.2.4 初始测试小结

通过首辆样车标载、超载与精确称重三个不同维度以及静态、动态两个不同场景下的测试，方形后桥半轴车型的公式Y5满足要求。表明该系统均具备良好的适应性和使用效果。尤其是在传感器数量不同的方案下，随着传感器数量的减少，精度相应地降低。结合降本需要，可灵活选择传感器数量，使该系统具有很强的应用实现能力。

以下将通过第二轮、第三轮测试对该系统方案进行优化并实现方案的标准化。

2 方案优化及标准化

2.1 方案优化

第二轮共选择两辆车，除已有的前面1#车，另选一辆同样技术状态的车辆，车号为2#。前面测试中，图1所示传感器布置方案存在部分选点安装困难情况。该轮测试对两车前桥传感器安装点进行优化，如图4所示，并使1#车与2#车安装点保持3 cm的距离差异，观测安装点差异对结果的影响。按照“1 初始方案设计及其可行性”方法，得到新传感器布置方案公式Y6。

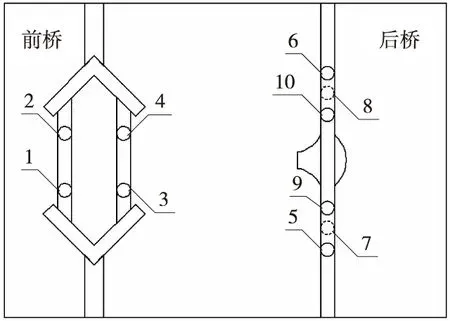
图4 传感器安装新方案

新方案下，按照前面描述的6个传感器与4个传感器选点方案分别测试，并选择称重误差10%作为参考标准。1#车和2#车测试结果见表5。

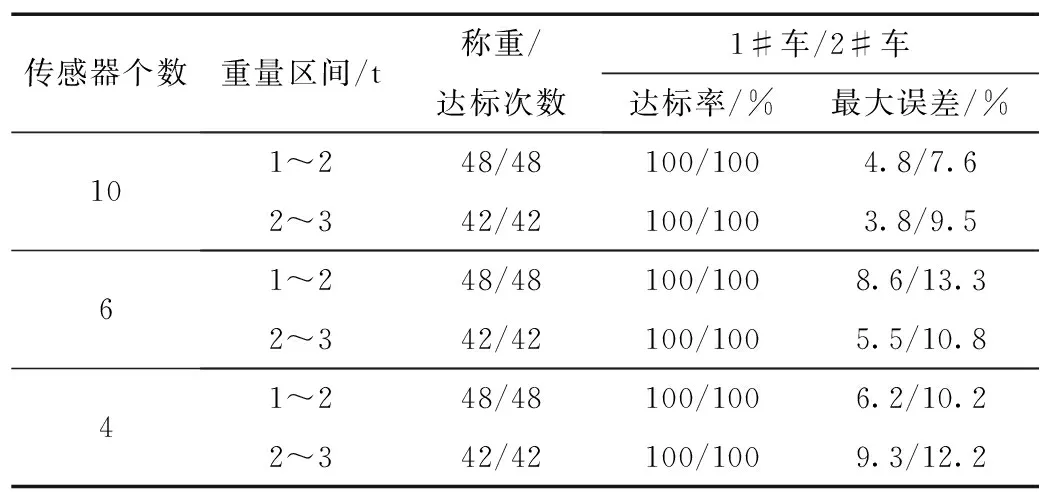
表5 1#车和2#车测试结果

1) 新方案下，两辆车整体测试结果良好并有一定差异，证明安装点的不同对计算公式和精度都有一定影响。但由于差异不大，后续若进行批量标准化安装，可允许一定范围的安装误差，提高安装效率。

2) 目前市场上，后桥半轴具有圆形半轴与方形半轴两种状态。下一步，在保持传感器安装点相对位置一致的情况下，测试不同的后桥半轴对公式和精度的影响，以及标准可研分析。

2.2 方案标准化

作正向开发设计方案，最重要的是要将方案进行标准化，以具备高效率下的批量生产能力和较高的一致性、可靠性。

此第三轮测试共计选择5辆车，除已有的1#、2#车，另选3辆车，车号为3#、4#、5#。其中，1#、2#、4#车的后桥半轴都为方形；3#、5#车的后桥半轴都为圆形。传感器数量都为10个，按照图4方案布置，前4后6。

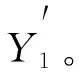
2.2.1 测试过程

1) 以1#车与3#车的计算公式，分别代表两种后桥半轴状态的方案。

2) 使用1#车公式Y6测试其他4辆车，观察该方案的适配性。

本轮通过两种不同车型的公式进行交叉测试，意在进一步分析和确定当前状态下，将通用性更好的公式作为标准公式。

2.2.2 测试结果及分析

1) 使用1#方形半轴后桥车的计算公式Y6，测试其他4辆车，部分数据见表6。

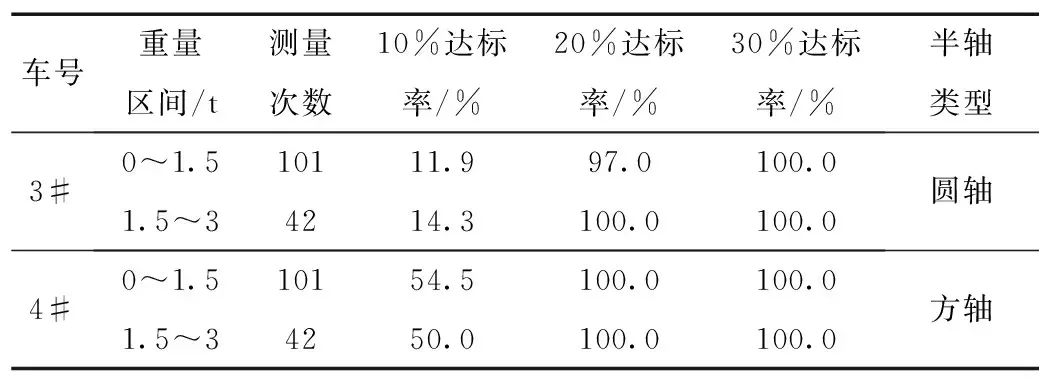
表6 1#车拟合公式测试部分结果

依据表6测试数据可以看出，方形半轴车辆公式下，该状态车辆的数据表现优于圆形半轴车辆。对比2#、5#另外两辆样车，与同状态车辆测试结果一致。

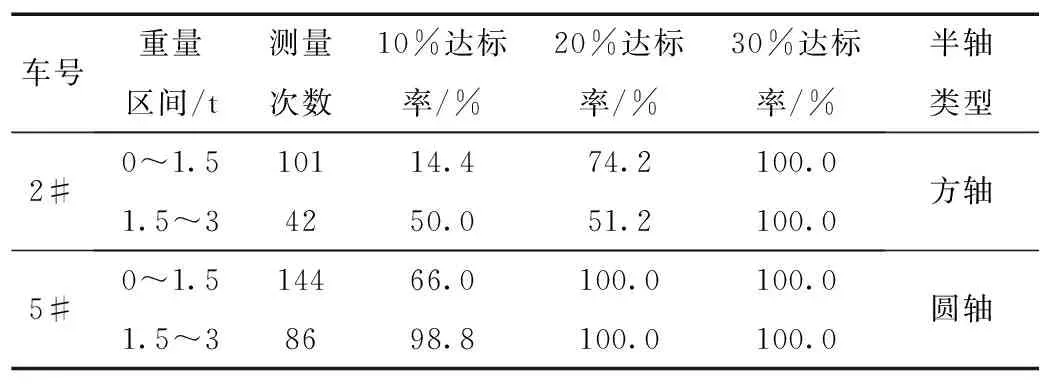
表7 3#车拟合公式测试部分结果

依据表7测试数据可以看出，圆形半轴车辆公式下，该状态车辆的数据表现则优于方形半轴车辆。对比1#、4#另外两辆样车，与同状态车辆测试结果一致。

所以，后桥半轴状态对公式有一定的影响，在精度要求较高的场景下，应根据后桥半轴状态选用对应的公式。总体来说，虽然方形与圆形半轴状态公式不是完全互相适用，但是结合市场上不同的应用场景，可在误差允许范围内适度互用，以降低生产及后期维护成本。例如，汽车厂商监控用户违规超载使用的行为，对精度要求较低，则可使用通用型公式。综上分析，方形半轴的计重公式整体测试结果较好，可作为通用型公式。

3 结束语

随着物流行业的快速发展，既为汽车产业带来巨大的需求促进，同时也提出了更高要求。未来智慧物流的发展，更要求汽车主机厂能够站在市场和技术的前沿，促进智慧物流的进一步发展[9]。