模糊逻辑与BP神经网络协同在刀具故障诊断中的应用

2020-11-02尤海鑫郭莎莎郭晓雨李伟芳

电脑知识与技术 2020年26期

尤海鑫郭莎莎郭晓雨李伟芳

摘要：BP神经网络具有自主学习、联想能力，它能解决许多常规信息处理方法难以解决或无法解决的问题;而不同测量设备提取的信号征兆参数各异，唯有将数据源模糊处理，即将二者结合，才能够优势互补，将其应用于数控机床刀具故障磨损的状态识别当中，具有较强的应用价值，为其提供了一条行之有效的解决途径。

关键词：BP神经网络;模糊逻辑;刀具故障诊断

中图分类号：TP18 文献标识码：A

文章编号：1009-3044（2020）26-0189-03

bstract： The BP neural network has the ability of autonomous learning and association， it can solve many problems that traditional signal processing methods are difficult to solve or can not solve;While different measurement equipments has different signs parameters.Only the data source fuzzy processed ， will the combination ofbothhavecomplementary advantages. If it is used in state identification of NC machine tool fault wear， it will have strong application value and provide an effective solution for it.

Key words： BP neural network ;fuzzy logic; tool fault diagnosis

数控机床刀具磨损故障是数控机床加工过程中的常见问题，机床刀具的磨损严重影响了加工工件的精度与质量，这些问题导致的停机故障制约着加工生产的效率，为此提出了BP神经网络和模糊理论结合的智能解决方法。BP网络作为神经网络最主导网络模型，依赖于多输入多输出的非线性特征和强有力的学习功能使其在系统辨识与自动控制领域得到广泛应用。现代故障诊断技术中不同设备信号征兆参数类型、数值大小各异，从这一角度，我们首先将具有随机性的设备提取信号做模糊化处理，然后与BP神经网络协同融合，成功将这一融合技术[1-3，7]应用到数控机床的刀具故障磨损的状态识别当中。

1 BP神经网络与模糊理论

1.1 BP神经网络理论

任何神经网络都是由大量的人工神经元相互连接而成的，典型的人工神经元由输入、处理、输出三部分组成，图1为人工神经元模型结构。

一般神经元的输入项为系统外部引入信号或与其连接的其他神经元输出信号，输入信号经过处理后得到一个结果，再把这个结果以信号形式输出到系统外部或作为其他神经元的输入。图中输入输出关系如下：

具体的，xn为输入信号，[yi]为输出信号;[netj]为神经元[j]的净输入;θj为神经元[j]的阈值， wj为连接权系数，表示xi与神经元连接的权值，wj为正时，表示与wj连接的神经元正处于兴奋状态，wj为负时，表示与wj链接的神经元正处于抑制状态;输出变换函数f（.）也称为激励函数。各种不同的人工网络数学模型的主要区别就在于对于不同的应用采用了不同的传递函数，从而使人工神经网络具有了不同的信息处理特性。

BP神经网络[4，6]是具有反馈功能的前向网络，学习过程中信号正向传播，误差信号反向传播。简单BP神经网络由三层组成：输入层、隐含层和输出层。学习过程如下：输入样本从输入层传入，在隐含层经过处理，再由输出层输出。当实际输出结果与期望值不符时，进入误差反向阶段，将误差信号以某种形式通过隐含层向输入层反向传递，同时将误差值分摊给各层的神经元节点（即调节神经元连接权值），这种信号的正向传播与误差信号反响传播交替进行的过程构成了BP神经网络的学习训练过程。

1.2模糊理论

定义：设U是一个用精确数据值表示的定量论域，C是U上的定性概念，若定量值[x∈U]，且[x]是定性概念[C]的一次随机实现，[x]对[C]的隶属度（确定度）为[μ（x）∈[0，1]]是具有稳定倾向的随机数。

一般认为，测控设备提取的征兆参数的值域、随机误差均可假定服从正态分布，因为我们选取高斯函数作为模糊化隶属函数。选取高斯函数[MF]，[MF]高斯函数完全由[δ]和C决定，[δ]是指高斯函数[MF]的宽度，C是指[MF]的中心。高斯函数[MF]对应的公式如下：

其中[C]点对应的值[xc]为高斯MF中的[C];不同类型数据对应的方差[δi]是高斯函数[MF]对应的[δ]。将设备某一时刻的样本数据[xi]带入此式可计算出相对应的隶属度函数[μi]。

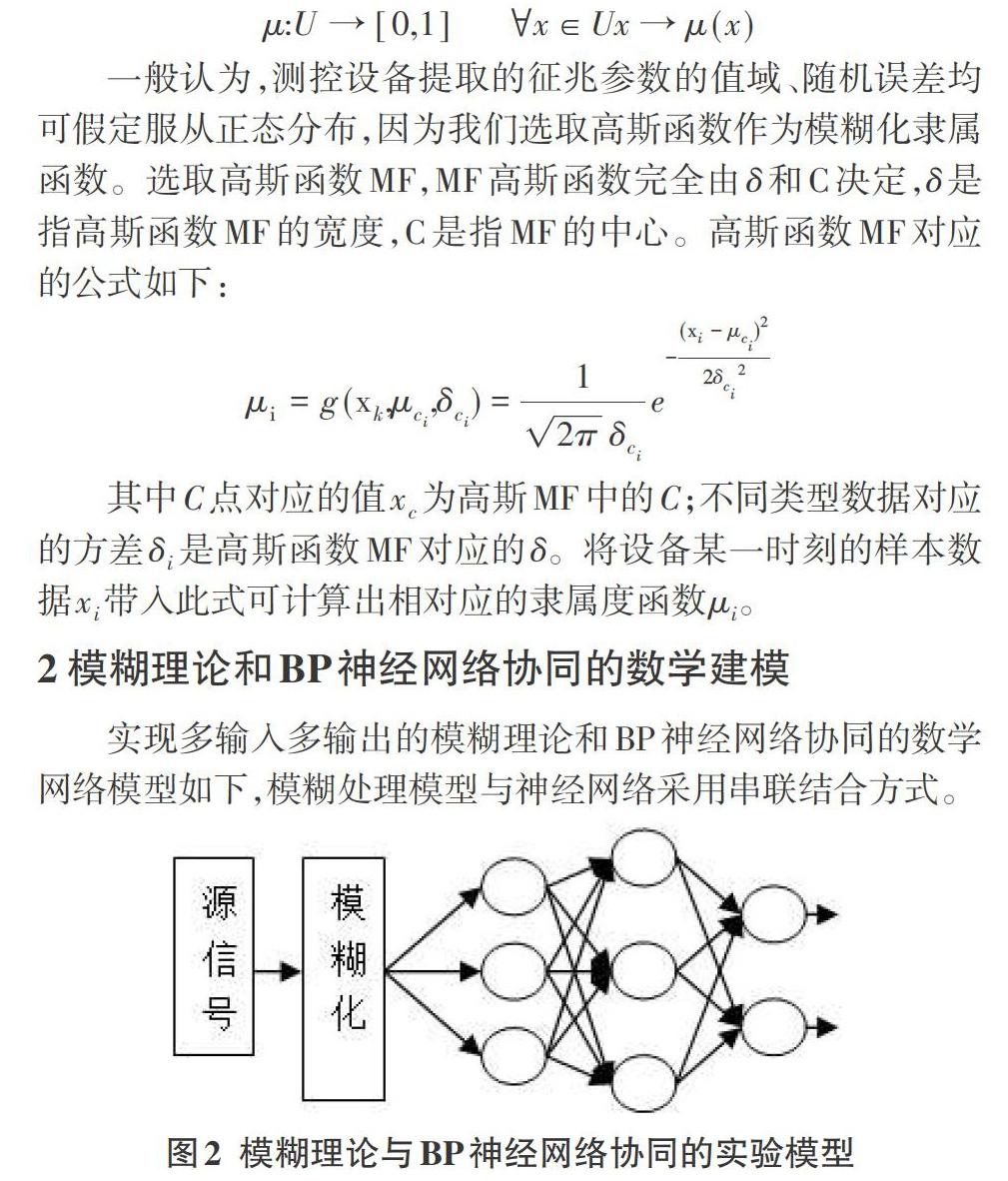
2 模糊理论和BP神经网络协同的数学建模

实现多输入多输出的模糊理论和BP神經网络协同的数学网络模型如下，模糊处理模型与神经网络采用串联结合方式。

该模型由输入层、预处理层、BP网络层三层组成，在输入层，其结点与输入层信号样本一一对应;经过预处理层，使用高斯函数MF对实验数据进行模糊化处理，然后传入BP神经网络层作为其输入数据。模型仍然保留BP网络有导师学习的机制，分为网络训练和测试两步。

BP模糊神经网络测试步骤如下：

（1）利用模糊化处理模型根据训练待测样本，求出输入属性的特征值，求出的特征值计算测试样本对应的隶属度;

（2）将步骤（ⅰ）得到的隶属度作为网络输入输出，进行BP网络学习训练;

（3）将试验样本数据进行实验仿真，从而得到网络的真实输出。

在实际情况中，往往会出现BP学习算法收敛速度很慢的问题，学习迭代过程往往需要几千步，于是为提高学习效率，提升算法的收敛速度，我们引入附加动量因子，该算法的引入使得迭代过程在动态或者自适应的变化来加速收敛，本文中我们选择了动量及自适应[IrBP]的梯度递减训练函数，学习效率[η]选择范围在0.0001～0.8之间。

3 实验和数据仿真

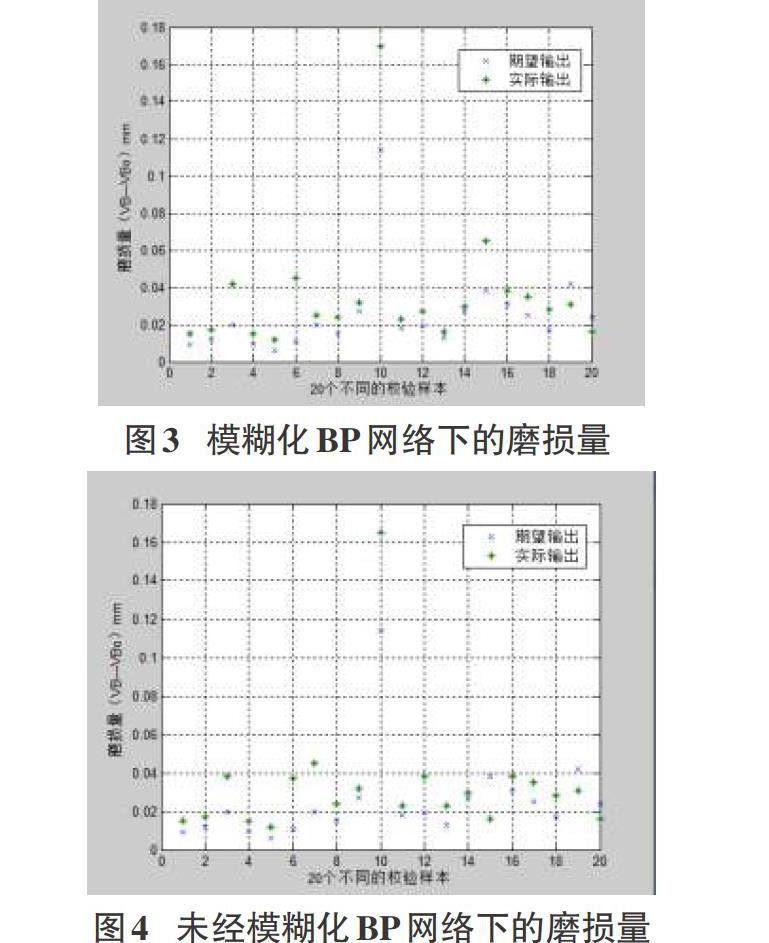
在文献——加工工况信息远程监测与刀具磨损识别技术的研究（路勇）[8]中，作者将基于移频小波包分解获得的4个AE信号特征向量（x1，x2，x3，x4）作为基于规则连接的5层模糊推理神经网络模型的输入，较好地解释了刀具磨损状态与监控参数之间的模糊关系，本文以文献[8]中表A-1数据中的AE的4个信号特征向量（即x1，x2，x3，x4）以及切削速度v、给进速度f、切削深度ap切削宽度ae共计8个特征信号作为训练样本输入，从输入数据我们可以看出，输入数据类型、数值大小形态各异，对实验数据的预处理工作成为必然。输出分两种情况讨论，第一将实际总体累计磨损量（VB表示）作为输出，二将磨损增量（VB—VBo表示）。文献[8]中表A-2数据作为测试样本，将模糊处理模型和BP神经网络协同的网络模型运用到刀具磨损故障识别中去。

通过上述表1的实验数据，我们可以非常直观地看出用预处理层模糊化处理的BP神经网络模型输出结果准确率远高于未经模糊处理的网络模型，用于刀具磨损状态识别准确可靠，其准确率达到80%，和文献[9]识别结果一致。

4結束语

本文提出的将模糊理论与BP神经网络相结合的刀具磨损诊断识别模型，既具神经网络的学习记忆功能，又结合了模糊理论的模糊性与随机性，过程简单明了，识别准确率远远高于简单BP网络，具有较强的实用性。

参考文献：

[1] 虞和济.故障诊断的基本原理[M].北京：冶金工业出版社，1989.

[2] 王江萍.机械设备故障诊断技术及应用[M].西安：西北工业大学出版社，2001.

[3] 王道平，张义忠.故障智能诊断系统的理论与方法[M].北京：冶金工业出版社，2001.

[4]王旭，王宏，王文辉.人工神经元网络原理与应用沈阳：东北大学出版社，2000.

[5] 焦李成.神经网络系统理论[M].西安：西安电子科技大学出版社，1990.

[6] 胡守仁，沈青，胡德文，等.神经网络应用技术[M].长沙：国防科技大学出版社，1993.

[7] 王士同.神经模糊系统及其应用[M].北京：北京航空航天大学出版社，1998.

[8] 路勇.加工工况信息远程监测与刀具磨损识别技术的研究[D].哈尔滨：哈尔滨工业大学，2000.