基于改进K-means的彩色图像分割算法

郭云云，高保禄，赵子润，杜 德，田 力

(太原理工大学 软件学院，山西 晋中 030600)

0 引 言

在图像的研究与应用中，往往只关注图像的某部分，如医学领域对图像病变区域进行检测等，都需通过图像分割把目标从整体图像中分离[1]。图像分割的效果直接决定后续图像分析和处理的结果，而现有彩色图像分割算法存在耗时长和分割效果不理想等问题[2]。因此，提出一种高精度和高效率的彩色图像分割方法是十分必要的。

目前的彩色图像分割方法主要有阈值分割法、区域分割法、聚类分析法和神经网络法等[3]。聚类分析法因其算法原理和图像分割性质极相似，一直被用于图像分割[4]。其中，K-means算法具有易于实现、简单高效的特性，应用最为广泛，但也存在对初始参数敏感等问题。对此，Aimi等[5]提出通过计算类内方差不断调整数据分类与中心点位置，该方法可自适应获取初始参数，但计算量大，降低了分割效率。文献[6]使用减法聚类算法估计初始中心的位置，分割结果质量得到提高，但没有摆脱对用户输入参数的依赖。Prahara A等[7]将直方图阈值和K-means算法结合确定初始参数，再对分割后区域进行分裂合并，损坏了物体的边界信息，导致分割线条不连续。以上算法采用了不同的方法获取K-means的初始参数，但相似度的计算都是采用像素位置的空间距离，特征单一，忽略了其它重要特征，可能造成像素点的错分类，使分割效果不理想。

基于此，本文提出基于改进K-means的彩色图像分割算法。通过图像的HSI颜色空间直方图自适应获得K-means算法的初始参数，减少对用户输入参数的依赖。然后提出提取图像的LDP(local directional pattern)纹理特征，构建像素点的纹理、颜色和空间坐标多维特征计算像素点间的相似度，克服仅使用一个特征的局限性，更好表示像素点的分布特征，使图像分割结果更符合人的主观视觉。

1 K-means算法及其在图像分割中的应用

K-means算法[8]通过预设分类数K和随机选取的初始中心点，不断迭代划分样本、计算聚类中心，使目标函数的值最优，即E值最小。K-means算法进行图像分割是根据像素点的特征对其进行聚类。

X={X1,X2,…,Xn}为含有n个样本数据的集合，{C1,C2,C3,…,CK}为K个中心点，两个样本点间的距离采用欧氏距离计算

Dist(Xi,Xj)=(Xi-Xj)2

(1)

聚类中心的更新方法

(2)

目标函数E定义为

(3)

其中，nj和Xj分别表示以Ci为中心点的子集中样本点的个数、以Ci为中心的子集中的样本点。利用K-means算法进行图像分割的具体步骤如下：

(1)输入彩色图像、分类数K；

(2)随机选取K个初始中心点；

(3)按式(1)计算其余像素点与初始中心间的距离，将其归类为最近的中心点所在的子集；

(4)更新类中心；

(5)循环步骤(3)、(4)直到中心点不再变化；

(6)返回分割结果。

可见，K-means算法进行图像分割存在的问题主要在于难以预先设定合适的分类数K和随机选取初始中心点造成聚类结果不稳定。另外，使用单一的空间距离特征计算像素间的相似度可能使像素点错分类，从而导致图像分割结果不理想。

2 自适应K-means初始参数计算

一些分割灰度图像的方法被用于分割彩色图像，但分割效果往往不理想，因为这些方法只考虑了图像的灰度值而不考虑色度。对于彩色图像，颜色是最有效且易获取的特征。因此，选择合适的色彩空间是很重要的。RGB颜色模型是目前硬件设备上显示图像数据应用最广的模型，它以R、G、B这3种分量的组合表示颜色。但由于各分量与亮度间具有高度的相关性，RGB空间对光照过于敏感，不适用于图像的分割[9]。因此本文使用HSI颜色空间，HSI颜色空间采用更符合人视觉系统感知色彩的方式，用色调、饱和度和亮度3种相互独立的特征量感知颜色，减少了对光照的敏感度，提高了色彩识别准确度。另外，独立的分量也便于分开处理，可以简化图像处理的工作量。为了降低计算复杂度并更好地区分相似颜色，对颜色进行量化[10]，得到颜色特征值L({Li∈Z+∪0|0 ≤Li≤ 71})。

本文提出的初始参数确定方法分为两步。一是构建图像的HSI颜色空间直方图，二是对其进行垂直与水平扫描。首先将颜色特征值L作为横轴，将落在每个颜色区间内的像素点总数(用P表示)作为纵轴构建图像的颜色直方图。然后对颜色直方图执行两次扫描操作：

(1)对特征值L进行垂直扫描，经扫描后特征值L须满足

PLi-1≤PLi≥PLi+1

(4)

经过垂直扫描后获得的峰值集合中可能存在彼此非常接近的特征值，即(Li≈Li+1)，易造成图像的过分割。因此，接下来将对颜色直方图进行水平扫描，来确定实际的峰值。

(2)将垂直扫描后得到的峰值集合中每个特征值与一定半径w内的峰值点进行比较，选择具有较高像素数的特征值L作为实际的峰值点，对于可能的峰值被选择为实际峰值Lr，必须满足以下条件

Lr=(PLp≥PLi) ∀PLi∈w

(5)

对图像的HSI颜色空间直方图进行两次扫描后，获得了具有最高峰值且相距较远的特征值L，将得到的实际峰值数作为分类数K，选择K个峰值特征值点作为初始中心点。

本文方法对颜色进行量化，构建HSI颜色空间直方图表示图像的色彩分布信息，计算复杂度低。峰值点处的颜色特征值在图像中出现的概率高，相隔一定距离可避免选择多个相似的特征值，这样得到的分类数更准确、中心点更能代表图像中各区域。

3 基于多维特征的相似度计算

K-means算法通过空间距离来计算像素点间的相似度，忽略了彩色图像像素点包含的其它重要特征，易造成像素点的错误分类。因此，本文提出提取图像像素点的LDP纹理特征，结合像素的颜色特征和空间坐标特征，构建像素点的多维特征向量。使用多维特征向量代替传统K-means算法中单一空间位置距离计算像素间的相似度，增加了相似性计算的特征条件，可以更准确反映彩色图像中像素点的分布，从而提高图像分割的准确性。

3.1 LDP纹理特征提取

首先使用LDP算法提取像素点的纹理特征，LDP[11]是Jabid 等提出的一种局部二进制模式的改进方法，常被用作潜在的特征提取方法。它可以通过比较不同方向上像素的相对边缘响应值来计算。给定图像中的中心像素，8个方向边缘响应值{mi}，i=0, 1,…,7。通常由Krisch掩模Mi在以像素位置为中心的8个不同方向上计算。8个方向的Kirsch模板如图1所示。

图1 Kirsch模板

由于不同方向响应值重要性不同，因此选择k个最突出的方向来生成LDP。top-k个方向响应值bi被设置为1，而其它方向比特值被设置为0。最后，LDP代码由式(6)、式(7)计算得到，其中mk是k个最重要的方向响应值

(6)

(7)

图2表示8个方向边缘响应位置和LDP二进制位位置。通常，k取3。

图2 8个方向边缘响应位置和LDP二进制位位置

本文先将图像分别与8个不同方向的Kirsch模板卷积，得到8个边缘响应矩阵；再对图像中的每个像素构造8位二进制LDP描述符，将二进制串转为十进制作为该像素的LDP特征。

LDP编码引入了二阶方向信息，大大减少了纹理信息的损失。另外，由于只对边缘响应绝对值排名前n位的方向编码为1，而梯度排名前n位的方向一般不会因噪声的影响改变位置[11]。因此LDP编码可以充分表达像素点的纹理特征，对非均匀光照不敏感。

3.2 多维特征相似度计算

将像素点的LDP纹理特征与颜色、空间坐标共同组成6个维度的特征向量。首先，HSI 颜色模型能很好模拟人的颜色感知，因此H、S、I这3个参数都被添加到特征向量中，用来描述像素点的颜色特征。然后，使用一个维度表示像素点的LDP纹理特征。最后，使用X，Y表示像素点在图像中的位置信息。因此，每个像素点i的特征向量可以表示为

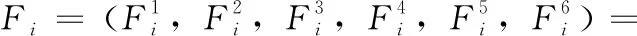
(8)

其中,i=1,2,…,N，N表示图像中的像素数，Hi、Si、Ii是像素i的颜色特征，LDPi表示像素i的纹理特征，Xi、Yi表示像素i的空间坐标。

像素点间的相似性距离通过多维特征向量的欧氏距离计算得到，公式如下

(9)

其中,dist(i1,i2)表示像素点i1和i2之间的相似性距离，F(i,m)表示第i个像素的第m个特征。

使用式(9)计算像素点到各个初始中心点的相似性距离，并将其分配给距离最近的中心点，形成K个子集，计算各子集中所有像素点的特征值均值作为新的中心，迭代执行直到中心点不再改变，输出分割后的图像。

基于改进K-means的彩色像分割算法流程如图3所示。

图3 算法流程

详细步骤如下：

(1)输入彩色图像；

(2)将图像由RGB颜色空间转换为HSI颜色空间，对HSI颜色空间进行非均匀量化，构建颜色直方图;

(3)对直方图进行垂直、水平扫描得到分类数K与初始中心点{C1,C2,C3,…,CK};

(4)提取像素点的LDP纹理特征，构建多维特征向量Fi;

(5)计算每个像素点与初始中心点间的相似度，并将其归类为最近的中心点所在的子集;

(6)更新类中心;

(7)迭代执行步骤(5)、步骤(6)直到聚类中心不再发生变化;

(8)输出图像分割结果。

上述算法步骤中，考虑了彩色图像像素点的色彩分布，自适应获取了合理的分类数和初始中心点。相似度计算时，对像素点进行具有良好视觉纹理特征的LDP编码，增加了特征约束，更充分表示了像素点的分布特征。另一方面，对颜色进行量化大大降低了数据量，更准确的初始参数和像素点的正确分类也使算法在较少的迭代次数内收敛。因此，本文算法可以大幅提升彩色图像分割效果，同时将时间复杂度保持在较低的范围内。

4 实验结果与分析

本文实验基于通用windows平台，使用Matlab对算法进行编程。计算机硬件环境为CPU (Intel@CoreTM i7． 3770 CPU@3.40 GHz)，显卡(AMD Radeon HD 7470)。实验用到的彩色图像与基准图像均来自Berkeley图像分割库[12]，每个图像的大小为481*321。

为了验证本文算法的有效性，将文献[6]算法、文献[7]算法、不引入多维特征计算相似度的本文方法与本文算法进行对比。在该实验中，文献[6]算法进行分割时聚类数K需要用户输入，实验直接取为基准值，算法所需其它参数选取最优值。3张图片分别命名为House、Swan和Flower，各算法分割结果如图4～图6所示。

图像House中各个部分之间有明显颜色差异，由图4可以看出文献[6]算法、文献[7]算法、不引入多维特征的本文算法和本文算法均将建筑与背景天空分离。但如图4中方框部分所示，其它算法分割结果存在线条不连续的缺陷，文献[7]算法受光照的影响较大，将建筑的屋顶部分错分为了两部分。而本文算法克服光照不均匀现象，成功将建筑主体、屋顶和天空分为3类，且线条连续完整。

图4 House分割结果对比

图5 Swan分割结果对比

图6 Flower分割结果对比

图像Swan中天鹅、影子、水面的颜色较为接近，增大了图像分割的难度。如图5所示，文献[7]算法将部分影子和水面错分为同一类，文献[6]和不引入多维特征的本文算法均未将天鹅的头部完整分割出来。本文算法分割得到的天鹅头部轮廓完整，很好的将天鹅与水面分离。

图像Flower中背景较为复杂。如图6所示，文献[6]算法只将花朵的主体外轮廓分割出来，对于细节部分分割的不够精细。文献[7]算法和不引入多维特征的本文算法的分割结果产生的碎片区域较多。本文算法将图像中的花朵花瓣和背景中的叶子部分有效分割，更接近基准分割结果，得到了较好的直观分割效果。因此，无论对颜色差异大或小的图像还是复杂图像，本文算法都可以得到较优的分割结果。

另外，为了客观评价各算法的分割效果，采用 MSE(mean square error)指标、PSNR(peak to signal noise ratio)[13]指标对各算法分割结果与基准结果之间的相似性进行定量分析。PSNR可通过式(10)计算，范围在[0,1)之间，越大越好。MSE使用式(11)计算，范围在[0,1]之间，越低越好

(10)

(11)

其中，S为255。M和N分别是输入图像中的行、列数。GI和SI是原始图像和分割后图像。

表1是文献[6]算法、文献[7]算法、不引入多维特征的本文方法与本文算法在House、Flower、Swan这3张图片上分割结果的MSE值、PSNR值比较。可以看出，本文算法在每张图像的结果评估中都获得了最优的客观指标值，表明本文分割结果更接近基准分割，与上文主观分析结果一致。

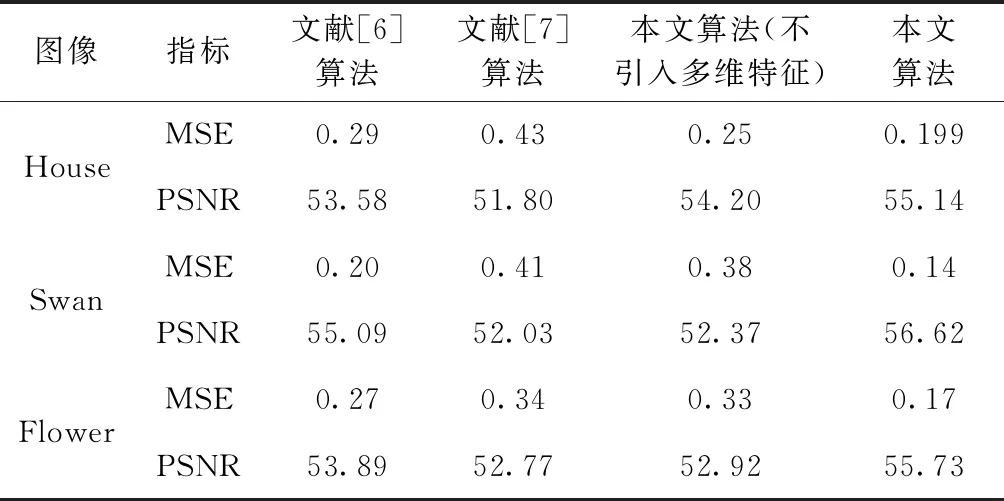
表1 各算法分割结果的MSE值、PSNR值比较

图7对各算法的运行时间做了对比。文献[6]算法迭代计算图像内所有的像素点，耗时最长。文献[7]算法采用直方图阈值法，在分割时间上与文献[6]算法相比用时较短。未引入多维特征计算相似度的本文算法通过颜色量化降低了计算复杂度，分割耗时远远小于其它两种算法。增加特征维度后计算复杂度增加，但合理的初始参数和像素点的正确分类使算法在较少的迭代次数内收敛，所以本文算法最终运行时间与文献[7]算法运行时间相当，短于文献[6]算法运行时间。

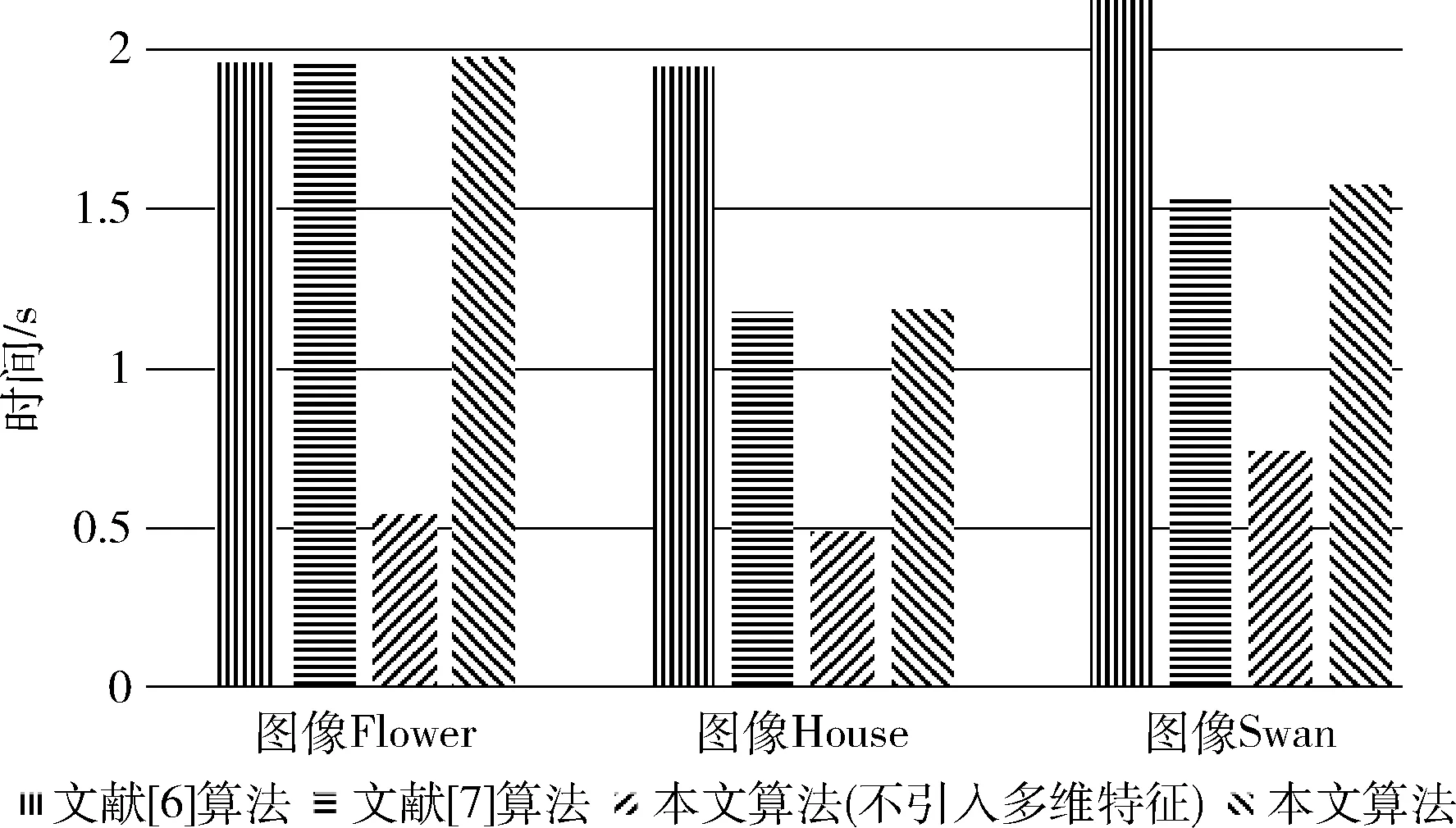
图7 各算法运行时间对比

5 结束语

针对k-means算法进行图像分割时依赖用户输入初始参数与分割效果不理想的问题，本文提出了一种基于改进K-means的彩色图像分割算法。首先通过图像HSI颜色空间自适应获得K-means算法准确的初始参数来表示图像各部分，减少对用户输入参数的依赖。然后提出构建多维特征向量计算像素间的相似度，降低了像素点的错分类率，使算法在较少的迭代次数内收敛，保证较高图像分割质量的同时保持较低的时间复杂度。

但是，本文算法仍存在不足之处，如在计算相似度时，多维特征计算使算法复杂度增加，导致算法运行时间较长，进一步提高算法效率是未来的研究方向。