无线传感器网络电量损耗异常节点识别

孙 璇

(北京信息科技大学 信息管理学院，北京 100192)

0 引 言

无线传感器网络(wireless sensor networks，WSNs)因其低成本、小型化和低功耗等特点，已经在多领域得到广泛的应用，同时也得到了学术界、工业界的广泛关注[1-3]。随着物联网的萌芽、成熟与推广，其安全问题逐步成为备受关注的首要问题[4,5]。

文献[6]中给出了无线传感器网络异常节点的定义，无线传感器网络中的异常节点是指网络中由于部分节点出现故障，导致采集的网络数据存在偏离的节点。已有很多学者在WSNs异常节点检测与定位方面提出了一些方法，这些方法主要分为基于统计学的方法、聚类分析的方法、分类方法和基于最近邻居的方法等[7,8]。随着压缩感知(compressed sensing，CS)理论在处理信号稀疏性方面的巨大应用潜力在各研究领域的实现[9,10]，其也在WSNs领域的数据收集与分析中逐步被广泛应用。在文献[11]中，首先给出了监控区域的稀疏数据模型。将监控区域网格化，并实现了用一个N维向量来表达该监控区域下的稀疏数据向量；然后通过理论论证了其在定位应用中的合理性；最后通过采用经典的贪婪匹配追踪方法实现了稀疏信号的重构。文献[12]在分析了WSNs无线链路不可靠导致的分组丢失现象的基础上，结合矩阵补全技术，提出了基于极稀疏块观测矩阵的压缩感知数据收集算法。目前压缩感知算法非常适合在WSNs场景下解决数据收集问题，而在当前WSNs中的安全问题凸显情况下，如何识别WSNs中的安全问题、如何应对WSNs中的安全问题也是当前亟待解决的问题。

首先对存在异常节点的WSNs进行场景建模，然后在此基础上采用LDPC校验矩阵进行线性测量，并根据基于图模型的置信传播算法进行重构从而判决。根据压缩感知的重构结果，即可以较高概率检测与定位WSNs中的异常节点。

1 问题描述

首先建立WSNs电量损耗异常节点识别算法的稀疏模型。将检测区域模拟为一个方形区域，其大小范围表示为ar×ar。在此假设基础上，将其均匀分割成数量为N2的大小相等的子区域，并假设每个子区域中至多存在1个处于工作状态的传感器节点。因此，可以将该检测网络中前一个检测周期的电量损耗用一个方阵来表示，记为G(N×N)。若某个子区域不存在传感器节点，则该节点对应的方阵中的元素应标记为0。异常节点检测与定位网络模型如图1所示，其中下层网络为用方阵G(N×N)记录的方形区域，区域中存在大量正常节点和少量异常节点；上层网络为观测节点，在每个检测周期，上层网络的某观测节点Mi负责下层网络数据的收集，并通过计算完成异常节点检测与定位。

图1 WSNs异常节点检测与定位系统模型

文献[13]中给出了不同协议层下，WSNs可能会遭到的一些攻击分类。在该文献中，按照物理层、链路层、网络层、传输层以及应用层，将网络攻击进行分类描述。每种攻击都有自己特定的方法和影响效果，因此针对这些攻击也需要有特定的防御策略。但是总结来看，大部分的网络攻击都会存在使得WSNs中的某个或某些关键节点能源耗尽的情况出现。比如虫洞攻击、邻居发现攻击、传输层的ICMP泛洪攻击、Synflood攻击等[14]。

因此，本算法通过数据整理、线性计算、恢复和判决3个环节识别出WSNs中的电量过快消耗的节点。如图1所示，在WSNs中，节点分为正常节点和异常节点，上层有观测节点实现数据的收集和处理。其中星形节点表示被攻击或其它原因导致的电量损耗过快的节点，圆形节点代表其中的正常工作节点。在方阵G(N×N)中，会存在某些电量损耗异常节点对应的位置的数值，会远远大于正常节点位置对应的数值。本文用电量损耗向量来表示整个区域中传感器节点的电量损耗，即

图2为某检测周期中的电量损耗向量V的仿真图示。从图2看出，受某种WSNs网络异常事件影响，WSNs中少数异常节点的电量损耗会明显高于其它正常状态传感器节点。根据压缩感知理论，如果信号是稀疏的，那么它可以由远低于采样定理要求的采样点重建恢复。由于该向量V是稀疏的，在异常检测算法中，不需要采集WSNs中所有传感器节点的电量损耗，只需要按照压缩感知的方式进行压缩采样，即可在观测端实现稀疏向量的重建从而做出异常节点的判决与定位。这样可以极大程度节省网络资源，延长网络寿命。

图2 4个连续周期的电量损耗向量(归一化)

2 异常节点检测定位算法

在建立好WSNs异常节点检测与定位系统模型之后，通过数据整理、线性计算以及重构与判决3个步骤来完成压缩感知的过程，从而实现对WSNs异常节点的检测与定位，异常节点检测定位算法步骤如图3所示。

图3 异常节点检测定位算法步骤

2.1 数据整理

数据整理包括两个步骤，首先是进行阈值计算。由于电量损耗向量V中正常节点也会产生一定的电量损耗，使得电量损耗向量V在时域的稀疏性不明显，并进一步影响数据重构的成功率和精度，因此需要先通过计算正常节点与异常节点的能量损耗阈值对稀疏向量V进行进一步整理。

文献[15]中给出了受攻击的WSNs中的无线电收发信息能量消耗模型。在距离为d的节点之间发送l-bit消息，需消耗的能量为

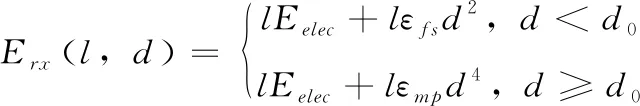
Eelec是接收机接收或者发射器发射l-bit信号所消耗的能量，εfs和εmp分别是自由空间耗散能量和多路径损耗能量。传感器节点的能量损耗主要来自于接收或发射数据包，且能量损耗主要受距离d的影响，而且当距离d大于d0时，能量损耗会更大

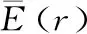
则

则XN2×1表示子区域传感器节点在检测周期r的电量损耗状态向量。根据具体情况对门限系数a进行合理取值，使得XN2×1中元素为1的个数非常少，即满足

则经过整理后的节点电量损耗状态向量为稀疏的01-向量。

2.2 线性计算

在数据整理阶段完成了用XN2×1表示子区域传感器节点在检测周期r的电量损耗状态向量。XN2×1为01-向量，且其中值为1的元素个数非常少，具有良好稀疏特性，因此可以对向量XN2×1进行压缩感知。

接下来是测量矩阵的选择。目前，高斯矩阵是最常见的被选作测量矩阵的情况，原因在于高斯矩阵与变换矩阵的不相干性强。但是在实际的应用场景下，这种随机矩阵在硬件上不太容易实现，是由于其效率低下，存储量又较大。本算法面向WSNs中的实际应用，因此选择LDPC码的校验矩阵作为测量矩阵，其元素只有0和1两种情况，因此硬件实现简单。测量矩阵的产生是用PEG(progressive edge growth)方式产生，其作为压缩感知的测量矩阵的合理性分析见文献[16]。

对XN2×1的压缩感知过程如下式所示

Y=ΦΨXN2×1

式中：Φ是LDPC码的稀疏校验矩阵，也是算法中线性计算采用的测量矩阵。该线性计算过程中的矩阵相乘过程，其涉及的加法是模2加的过程。式中的矩阵Ψ是为稀疏域的基底矩阵。另外，因为电量损耗状态向量XN2×1中1的元素远小于向量元素个数，因此其在时域就是稀疏的，故Ψ=I。在观测端Mi进行数据收集的线性计算，得到观测结果Y。

2.3 重构和判决

重构阶段依据上一阶段所得观测结果Y与测量矩阵Φ实现电量损耗状态向量的重构。由于测量矩阵为LDPC码的校验矩阵，因此重构过程即为LDPC码的译码过程。最经典的LDPC译码算法就是置信传播算法(belief propagation，BP)。由于译码时主要涉及加法运算和乘法运算,所以BP算法也被称作和积算法。BP算法需要将LDPC码首先映射为一个Tanner图，然后通过信息在Tanner图上的不断迭代过程，从而达到收敛[17]。图4为LDPC校验矩阵与Tanner图的对应。

图4 LDPC校验矩阵与Tanner图对应

通过在Tanner图上的消息传递过程实现和积算法的迭代过程。当信息在校验节点和变量节点之间的交互和迭代达到一个收敛状态的时候，即可得到电量损耗状态向量XN2×1的估计值。

根据置信传播算法得到的节点电量损耗状态向量的估计值，其中元素值为1对应的传感器节点，即被判决为在本检测周期电量损耗过高的节点。在下一检测周期的路由算法中，应尽量避开这样的节点。

如果在连续的N个检测周期内，都发生某节点电量损耗过高的现象，即应被判决为异常节点，从网络中剔除。

3 仿真分析

3.1 仿真场景

仿真场景如图5所示，监控区域为方形区域，按一定规则部署传感器节点。在某些异常事件影响下，某些传感器节点的电量会消耗很快。如图5所示，黑色圆圈标注的是因为遭受DDoS攻击或因为其它情况(如负载不均衡)导致的电量快速消耗的节点。这些节点在向量XN2×1中对应的值为1，其它节点对应的值为0。

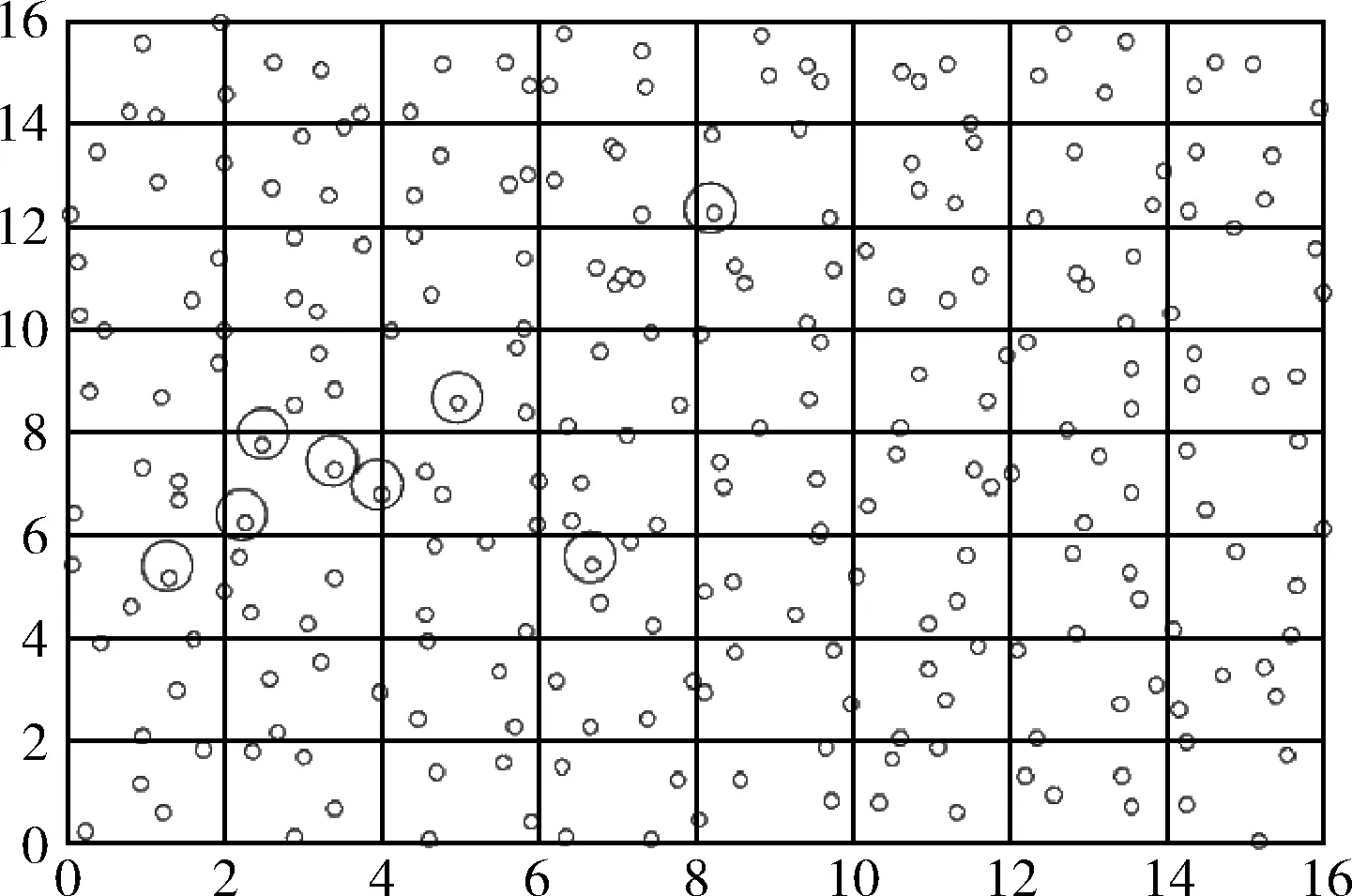
图5 算法仿真场景假设

压缩感知所选用的LDPC稀疏校验矩阵的行重L根据传感器节点的个数设定。在每个检测周期，观测端某观测节点Mi按一定规则生成用于压缩感知的测量矩阵，并对WSNs中的部分节点进行电量损耗信息收集并完成线性计算。在观测端得到测量结果Y之后运行置信传播算法进行重构并判决。仿真使用MATLAB R2014b运行。

3.2 仿真结果

从图6可以看出，算法的检测概率受测量矩阵影响明显。仿真中假设节点电量损耗向量长度是1024，异常节点个数为5。第一个影响因素是行重L，在稀疏度已知且不变的情况下，行重L越大，则算法的检测概率越高。第二个影响因素则是测量矩阵的测量数M，M越大，算法的检测概率也越高。行重L与测量数M的设置越高，则算法越精确，但同时带来的是算法成本的上升。

图6 不同矩阵行重对检测概率的影响

从图7可以看出，在固定的测量矩阵参数设定下(测量个数M与行重L均相同)，算法检测概率主要受电量损耗状态向量的稀疏度影响。通过置信传播算法对电量损耗状态向量的重构效果受原始信号的稀疏度影响较大。在满足K≪N条件时，原始信号是稀疏的。也就是在WSNs场景下，只有当能量消耗异常的节点远小于总传感器节点数的条件下，该算法可以有效节省网络成本并能够重构WSNs的电量损耗状态向量。稀疏度K越大，就需要在构造测量矩阵时，设定较大的M值与L值，才能够达到精确重构。

图7 不同稀疏度对检测概率的影响

图8为不同测量矩阵的检测概率对比。在该实验过程中，将信号长度固定、信号稀疏度固定，测量数M从200到600的变化区间中，选用不同的测量矩阵从而比较其对算法检测概率的影响。从图8可以看出，相比选用高斯矩阵、傅里叶矩阵，本算法选用LDPC的校验矩阵作为测量矩阵有更高的检测概率。这是因为LDPC矩阵作为测量矩阵，其具有更高的正交性和更低的相关度的影响。

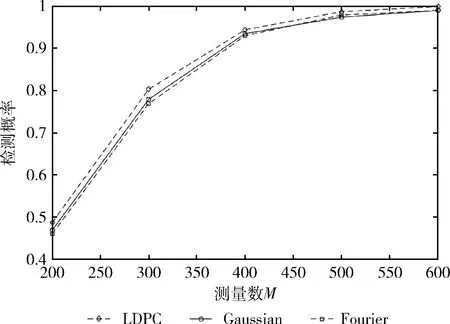
图8 不同测量矩阵的检测概率对比

仿真结果表明，本文提出的异常节点检测定位算法能够通过合理设置测量矩阵对节点电量损耗状态向量进行线性计算，并通过置信传播算法实现精确重构从而判决。与其它压缩感知方案的性能对比结果表示，选择LDPC的校验矩阵相比传统的压缩感知方案有更好的检测概率。在实际应用中，测量矩阵的设置可以依据上一周期的重构结果去调整行重和测量个数从而达到期望的定位结果。

3.3 计算复杂度

本文提出的基于压缩感知的WSNs异常节点检测定位算法的重构是基于置信传播的LDPC译码。为降低计算的工作量和复杂度，文中提出的异常节点检测定位算法以节点电量损耗状态为测量值，将状态值用0或1来表示，大大简化了译码的难度。该测量值在网络中易于获取，不需要额外的测量设备和通信设施。通过仿真也验证了合理的调整行重或测量数，可以以不多的代价达到较好的检测概率结果。

4 结束语

本文提出了一种基于压缩感知的WSNs异常节点检测定位算法。依据WSNs电量损耗状态向量的稀疏性，采用压缩感知的方式进行数据整理、线性计算、重构与判决3个步骤完成异常节点的识别与定位，对WSNs异常检测研究有一定借鉴意义。后续工作将进一步分析该方法在稀疏度时变条件下的自适应方案从而优化该算法的可靠性与实用性。