Rayleigh型槽波的频散特征及影响因素
2020-11-02樊斌,匡伟
樊 斌,匡 伟
(1. 潞安集团五阳煤矿,山西 长治 046000;2.常州泽南软件科技有限公司,江苏 常州 213200)
当多层介质中有一低速层时,因其地震波速度比围岩低,分界面处形成强反射界面。在低速层中激发震源,部分振动能量将被禁锢于低速层内,在其边界产生来回多次全反射并产生叠加,形成一类特殊的干涉波沿低速层传播,该低速层就成为波导层,在波导层内传播的波即为槽波。煤系地层中,地震波的传播速度小于围岩,因此可将煤层看成为一个条带形的低速煤槽。煤层中的地震波通常包含SH型横波、SV型横波以及纵波,由SV型横波、纵波相互干涉形成Rayleigh型槽波[1-2]。槽波最大的特点是能量强、传播距离远。组成槽波的各个频率在低速带中的传播速度不一致,形成频散[3-5]。槽波拥有其它地震波没有的特征,即:埃里震相的存在。Airy相的特点是速度低,频率高,通过相应的数据处理手段,可利用Airy相信息来有效地推算勘探区域的相关地质信息。本文通过对槽波频散特征的研究,建立不同地质模型,推导理论公式并进行计算,为槽波探测数据的分析、Airy相识别、数据处理提供依据。
1 面Rayleigh型槽波频散方程[6-8]
建立图1所示直角坐标系,假设原点位于煤层中心,地震波沿着y轴方向传播,x轴垂直纸面,z轴垂直向下。煤层厚度为2d,ρi、μi、vSi、vPi(i=1,2,3)分别代表顶板、煤层和底板的密度、拉梅常数、横波速度和纵波速度。

图1 单一煤层剖面图及其柱状图
Rayleigh型槽波是由P波和SV波相互相长干涉形成,取SV波和P波的满足波动方程的势函数如下:
(1)
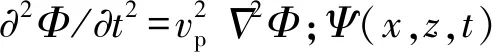
(2)
求解式(2)。在顶底板介质中,利用z→±∞,位移值为有限值的边界条件,最终解得:
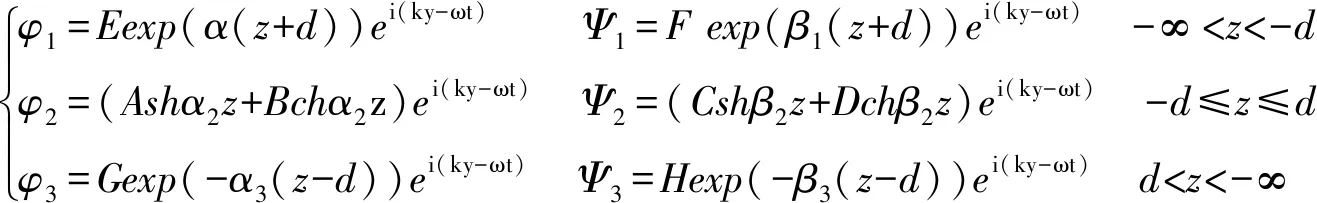
(3)
式中,
而纵横波在相邻分界面需满足位移、应力连续的边界条件:
(4)
纵横波的位移函数、正应力、剪应力的表达式如式(5)~式(8)。将纵横波势函数代入式(5)~式(8)即可求得分界面上各个地层的纵横波位移、正应力以及剪应力。
(5)
(6)
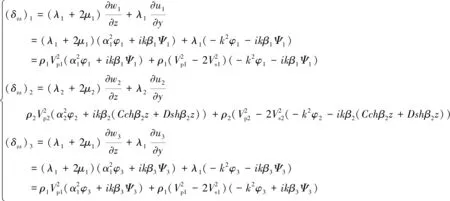
(7)
(8)
将位移、正应力、剪应力表达式代入边界条件(4)可求得8个齐次方程。为使8个待定系数A、B、C、D、E、F、G、H不同时为零,必须令系数行列式为零,即得到[9-10]
(9)
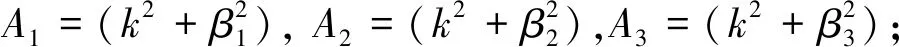
B1=2ikα1,B2=2ikα2,B3=2ikα2;
C1=2ikβ1,C2=2ikβ2,C3=2ikβ3;
上式(9)即为三层瑞利型槽波的频散方程,解此方程得到三层瑞利型槽波频散曲线。
2 Rayleigh型槽波频散特征影响因素
2.1 煤厚与Airy相位频率、速度关系
建立4个地质模型,对应序号①~④,各模型的主要参数为煤层纵波速度vP2、煤层横波速度vS2、围岩纵波速度vP1、围岩横波速度vS1和围岩与煤层密度比值ρN。
假设各模型的煤层厚度2d是变化的,取值分别为3 m、5 m、7 m和9 m,其他参数保持不变。煤层纵波速度vP2、煤层横波速度vS2、围岩纵波速度vP1、围岩横波速度vS1、以及围岩与煤层密度比值ρN取值分别为 1 710 m/s、900 m/s,2 808 m/s、1 800 m/s和2。将上述地层参数代入单一煤层Rayleigh型槽波频散方程,并计算出频散曲线如图2所示,从图中可以看出,当煤层厚度增加时,Airy相频率明显降低,Airy相速度也略有降低。

图2 Rayleigh型槽波频散曲线
2.2 煤层速度与Airy相位频率、速度关系
(1)煤层横波速度变化
建立2.1中类似的模型,煤层横波速度vS2不断变化,而其他参数保持不变。煤层横波速度vS2取值分别为900 m/s、1 000 m/s、1 100 m/s和1 200 m/s,煤层纵波速度vP2、围岩纵波速度vP1、围岩横波速度vS1、围岩与煤层密度比值ρN以及煤层厚度2d分别为 1 710 m/s、2 808 m/s、1 800 m/s、2和3 m。将上述地层参数代入单一煤层Rayleigh型槽波频散方程,并计算出频散曲线如图3所示,从图中可以看出,随着煤层横波速度的增加,Airy相频率和速度相应升高。
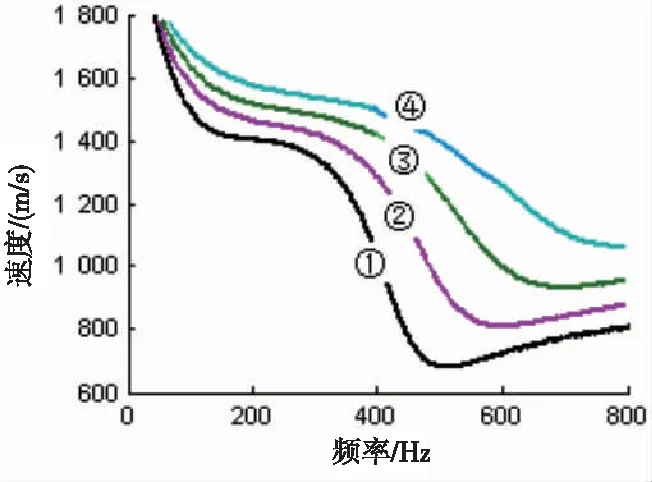
图3 Rayleigh型槽波频散曲线
(煤层横波速度900~1 200 m/s计算的结果曲线分别对应①~④曲线)
(2)煤层纵波速度变化
建立2.1中类似的模型,煤层纵波速度vP2不断变化,而其他参数保持不变。煤层纵波速度vP2取值分别为1 710 m/s、1 810 m/s、1 910 m/s和2 010 m/s,煤层横波速度vS2、围岩纵波速度vP1、围岩横波速度vS1、围岩密度与煤层密度比值ρN以及煤层厚度2d分别为 1 710 m/s、2 808 m/s、1 800 m/s、2和3 m。将上述地层参数代入单一煤层Rayleigh型槽波频散方程,并计算出频散曲线如图4所示。从图中可以看出,随着煤层纵波速度的增加,Airy相频率和速度变化较小。

图4 Rayleigh型槽波频散曲线
(煤层纵波速度1 710~2 010 m/s计算的结果曲线分别对应①~④曲线)
2.3 围岩物性与Airy相位频率、速度关系
建立2.1中类似的模型,围岩与煤层密度比ρN不断变化,而其他参数保持不变。各模型的围岩与煤层密度比ρN取值分别为1.5、1.8、2.0和2.2,煤层纵波速度vP2、煤层横波速度vS2、围岩纵波速度vP1、围岩横波速度vS1、以及煤层厚度2d分别为1 710 m/s、900 m/s,2 808 m/s、1 800 m/和3 m。将上述地层参数带入单一煤层和Rayleigh型频散方程,得到图5所示的不同围岩与煤层密度比的频散曲线,可以看出Rayleigh型槽波的Airy相频率基本不受围岩与煤层密度比影响。
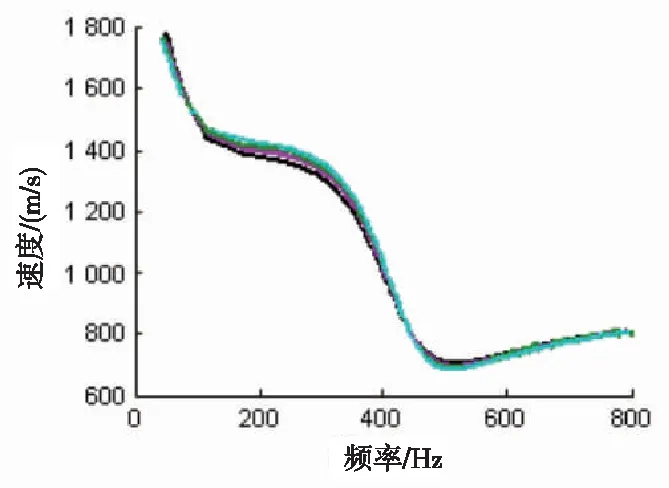
图5 Rayleigh型槽波频散曲线
2.4 Airy相位与煤厚、煤层横波速度综合关系
由2.1~2.3计算结果可知,煤层横波速度、煤层厚度与Rayleigh槽波的Airy相频率和速度关系最为密切,而煤层纵波速度、围岩与煤层密度比对Airy相的影响较小。
因此设计煤层横波速度、煤层厚度两个参数同时变化的地质模型。其中,煤层厚度2d取值分别为2 m、3 m、4 m、5 m、6 m、7 m、8 m,煤层横波速度vS2取值分别为900 m/s、1 000 m/s、1 100 m/s、1 200 m/s、1 300 m/s,其他参数保持不变。煤层纵波速度vP2、围岩纵波速度vP1、围岩横波速度vS1、围岩密度与煤层密度比值ρN分别为 1 710 m/s、2 808 m/s、1 800 m/s。将各参数模型代入Rayleigh型槽波单一煤层的频散曲线方程。将各模型计算的结果绘制成曲线图,如图6所示。
可见,槽波Airy相频率是煤层厚度以及煤层横波速度的函数,当煤层越薄、横波速度越高,槽波的Airy相频率越高。Airy相频率随着煤层厚度的增加逐渐降低,近似为指数关系,随着煤层横波速度的降低,Airy相频率逐渐降低。图中从左至右分别对应基阶、一阶以及二阶频散方程计算结果,基阶、一阶以及二阶均呈现相同趋势。
3 结 论
(1)煤层厚度、煤层横波速度对Rayleigh型槽波频散特征影响较大。随着煤层厚度增加时,Airy相频率明显降低,Airy相速度也略有降低;随着煤层横波速度的增加,Airy相频率和速度相应升高。
(2)围岩与煤层密度比、煤层纵波速度对Rayleigh型槽波频散特征影响较大。Rayleigh型槽波的Airy相频率基本不受围岩与煤层密度比影响;随着煤层纵波速度的增加,Airy相频率和速度变化较小。
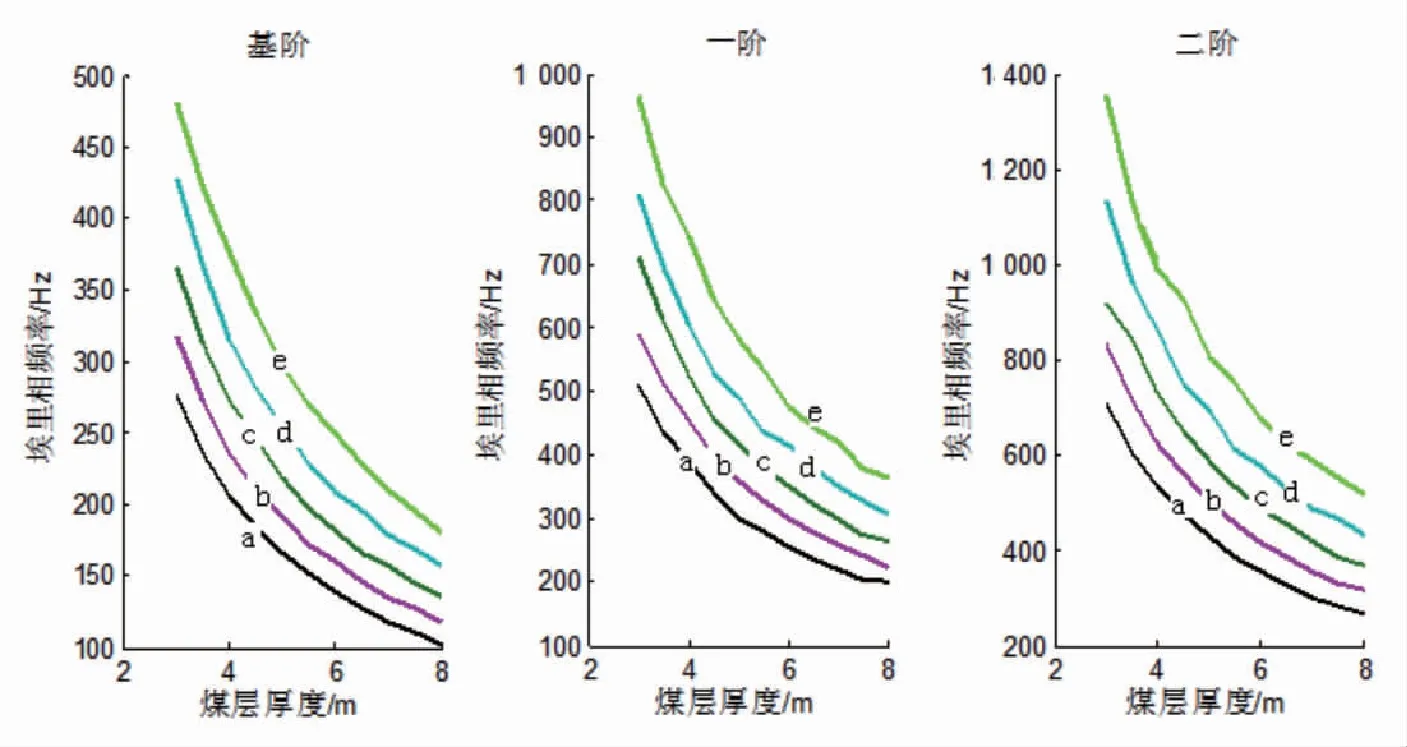
图6 Rayleigh型槽波Airy相频率与煤层厚度、煤层横波速度的关系曲线
(3)槽波Airy相频率是煤层厚度以及煤层横波速度的函数,当煤层越薄、横波速度越高,槽波的Airy相频率越高。
