融合LSC和REHSM的地壳形变分析模型*
2020-11-02钟光伟符平贵
钟光伟,符平贵,杨 钢,张 俊
(贵州大学 矿业学院, 贵州 贵阳 550000)
传统地壳运动模型大都是基于欧拉定理建立的刚体运动模型。这些模型大多都是将地壳运动看作是一种地壳表面的刚性运动,认为板块内部没有或不考虑板块内部形变[1-2]。自20世纪90年代以来,许多研究成果表明板块运动不完全是刚性运动,板块边界并非狭窄的而是可以发散的,即板块运动不全部发生在相邻板块一定范围的边界带上,且板块内部也存在不同程度的不规则形变[3]。我国学者李延兴等研究了板块内部形变性质,于20世纪初提出了块体运动的整体旋转与均匀应变模型,这种模型假定块体内部形变在空间分布呈均匀变化,只要在传统刚体运动模型基础上拓展描述板内均匀形变的参数,即可解算出块体内部形变量及应变参数。这使得板块旋转参数与均匀应变参数得以进行整体解算,实现了真正意义上的地壳运动-形变的综合模型[4]。但是,鉴于不同的地质环境和构造运动的复杂性,整体旋转与均匀应变模型对块体内部形变的均匀假设仍然具有相当局限性。事实证明,块体内部形变性质及规律相当复杂,任何简单假设都难以精确描述。鉴于此,本文提出利用最小二乘配置模型与地壳运动的整体旋转与均匀应变模型相融合,即利用整体旋转与均匀应变模型作为地壳运动的主模型,但同时认为这种模型还难以精确描述全部地壳运动,因此尝试用“信号”补偿偏离整体旋转与均匀应变模型的地壳运动部分,从而建立一种优化的整体旋转与均匀应变最小二乘配置地壳形变分析模型。
1 整体旋转与均匀应变模型及最小二乘配置模型
1.1 刚体运动模型(RRM)
早期的地壳运动定量化模型是基于板块构造运动理论根据球面刚体运动的欧拉定理提出的,其运动模型为[4]:
(1)
式中,Ve与Vn分别为站心参考坐标系中的纬向(东向)速度和经向(北向)速度;λ、φ为经纬度;ωx、ωy、ωz为欧拉旋转参数;r为地球的平均半径。
1.2 板块的整体旋转与均匀应变模型(REHSM)
在研究板块运动的整体旋转和均匀应变模型时,通常采用球面正交坐标系。由于球面上经纬线是处处正交的,所以可以以块体所包含区域的几何中心(λ0,φ0)为坐标原点,以过原点的纬线为x轴、经线为y轴,建立坐标系。即可得到坐标与经纬度之间的转换关系如下
(2)
若在研究地壳运动模型时,考虑的不仅仅是块体的刚性整体旋转运动,则这种模型称为非刚体板块运动模型。地壳在绕某一固定轴旋转的同时,板块内部也会伴随着不同程度的弹塑性运动。顾及到板块内部运动形变,李延兴等学者提出由板块刚性整体运动和弹塑性运动复合而成的地壳运动模型[4-7,9-11]:
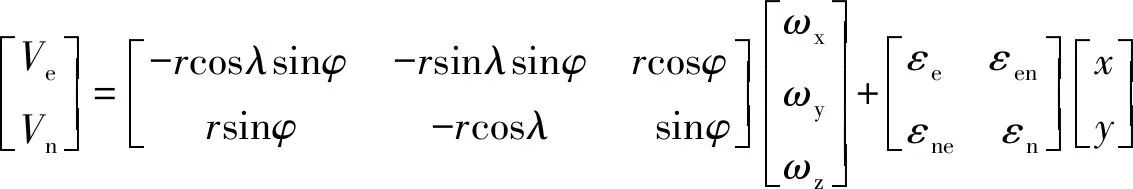
(3)
式中,εe、εn、εen、εne为应变参数;其他参数含义与式(1)和式(2)相同。
1.3 最小二乘配置模型(LSC)
最小二乘配置模型的一般形式为[4-5,11]:
L=AX+BY+Δ
(4)
式中,A为倾向参数的系数矩阵;X为倾向参数;Y=[SS′]T为信号;Δ为噪音。
(5)

已知点和未知点的信号估值为
(6)
式中,DS为已测点协方差;DS′S为已测点和未测点之间的协方差。
在应用最小二乘配置法时,最关键的问题是要事先确定信号间(包括已测点和未测点)的方差-协方差矩阵。在地壳运动中,根据经验凡是具有随距离衰减性质的函数,理论上都可以用来构造地壳运动分析的协方差函数,高斯指数函数是地壳运动中最为常用的一种。高斯函数法表示法为[4,8]:
C(S)=C(0)exp(-k2s2)
(7)
式中,C(0)和k为待估参数。
2 融合最小二乘配置与整体旋转与均匀应变的分析模型(LSC-REHSM)
地壳形变分析的整体旋转与均匀应变模型较好地发展了基于欧拉定理的刚性旋转运动模型,但鉴于不同地质构造区域的块体,其整体运动模式及局部构造形变都极不规则,故对地壳内部一点的应变做“均匀”处理仍是一个很强的假设,难以适用于具有复杂地质构造的区域[4]。如果仍然采用REHSM描述地壳运动,则既不能精确地描述板块的整体运动,也不能正确地反应出板块内部的运动形变。本文采用最小二乘配置模型中的信号来补偿偏离板块均匀应变的地壳形变部分,从而优化整体旋转与均匀应变模型。具体模型为:

(8)
式中的符号含义与式(1)、式(3)和式(4)的意义相同。
3 算例及分析
本文数据来源于文献[13]给出的喜马拉雅-西藏板块在ITRF97参考框架下GPS观测的速度场数据,共有测站54个,速度场均经过GIPSY软件解算获得,速率平均中误差小于2.4 mm/a。现分别采用如下三种方案对该区域GPS速度场数据进行拟合分析,结果列于表1,为直观,同时绘制了三种方案的拟合残差,如图1所示。
方案1:地壳刚体运动模型(式1)
方案2:整体旋转与均匀应变模型(式3)
方案3:整体旋转与均匀应变模型的最小二乘配置模型(式8)
表中速率残差标准差计算公式如下:
(9)
式中,Δvei,Δvni分别为第i个测站在东方向和北方向运动速率的残差;R为未知数参数个数;n为测站个数。

图1 3种模型残差比较成果图

表1 3种模型的欧拉运动参数及速率残差标准差
对计算结果分析如下:
(1)从表1给出的速度场拟合残差标准差可以看出,方案1采用的RRM模型由于未顾及块体运动的内部形变,其残差拟合标准差最大;方案2采用的REHSM模型,由于考虑了块体运动的板内形变,其标准差明显小于刚体运动模型。但是鉴于喜马拉雅-西藏板块体复杂的地质环境,这种简单假设块体内部形变是均匀的将很难与本区域地壳运动有最佳的符合,而方案3采用LSCREHSM模型,利用信号对方案2未能描述的地壳形变部分进行了补偿,从而取得了更小的拟合残差标准差,获得了最佳的拟合结果;
(2)从图1对喜马拉雅-西藏板块GPS速度场的拟合残差分布图可以看出,RRM、REHSM和LSCREHSM三种模型在东西和南北方向的拟合残差整体上都是依次减小的,其分析结果与表1结果完全一致。再一次表明,本文采用信号补偿偏离整体旋转与均匀应变的地壳形变部分是有效的,同时也说明喜马拉雅-西藏板块地壳运动及形变规律非常复杂,采用刚体运动模型不能正确描述其运动规律,而简单采用整体旋转与均匀应变模型来改善刚体运动模型在喜马拉雅地区其改善效果也十分有限。本文尝试采用信号描述和补偿整体旋转与均匀应变模型所不能表达的地壳形变部分,进一步改善了刚体地壳运动模型,最终取得了非常好的改善效果。
4 结 语
传统基于欧拉定理的地壳刚体运动模型不顾及板内形变,无法精确描述地壳实际运动。而地壳运动的整体旋转与均匀应变模型假定块体内部形变是均匀的,这对于具有复杂地质构造运动的区域仍然具有相当局限性。本文将块体内部不规则形变看作信号,对整体旋转与均匀应变模型进行了改善,其实质是对形变的“均匀”假设进行了修正,修正量为偏离块体运动的整体旋转与均匀应变模型所描述的运动之外的那部分形变。
本文采用LSC-REHSM应用时,需要确定信号的协方差函数,采用不同的协方差函数会得到不同的拟合结果。本文采用高斯指数函数计算信号的协方差矩阵,得到较好的拟合分析结果,但在应用中,如何选择协方差函数仍然是值得进一步探索和研究的问题。
