屋顶钢结构广告牌自振周期计算方法研究

完海鹰，沙浣玲，陈安英 （合肥工业大学土木与水利工程学院，安徽 合肥 230009）

0 前言

近年来，随着生产力水准的提高和科技的成长，我国经济建设取得了引人注目的成绩。伴随我国社会经济成长体系的不断变化，广告业也在发展中。而作为高耸结构的户外广告牌是一种常见的广告载体，十分受到广告行业的青睐。

户外广告牌包含广告牌面板、照明以及其他必要的设备。2003年，《户外广告设施钢结构技术规程》[1]在我国开始施行，自此户外广告牌的建造走向了正规化。其中屋顶广告牌结构设立在楼顶，属于风敏感结构，风荷载对其结构分析起了重要的控制作用，根据风荷载公式，结构自振周期的取值将影响风荷载计算。结构自振周期是结构自身十分重要的动力特性，是影响脉动风作用的一项主要因素，结构越高其自振周期越大，与脉动风周期更为接近，则结构所受风荷载作用更大[2]。

在规范中规定对屋顶广告牌的自振周期取值说明为最好采用整体结构进行计算，并同时考虑自身结构，而实际设计中，一般原结构模型存在丢失而本身结构形式复杂，层数众多且结构形式多样，如此要复原模型，不仅费时费力且有一定难度。所以大多数设计人员选择只单独考虑广告牌自身结构效应，这样简化是及其不安全的。这就需要一个较合理的计算方式，在方便计算的同时，也可以保证结构设计的安全性。

本文将对广告牌自身、原结构自身及广告牌与原结构整体进行模态分析，对比其基本自振周期，以确定更优的屋顶广告牌自振周期计算方法。

1 计算模型建立

选择Midas软件建立模型，模型所建一系列结构拟建于安徽省合肥市某郊区，基本设计信息如下：抗震设防烈度7度（0.10g），设计地震分组为第二组，基本风压采用五十年一遇基本风压0.35kN/m2，地面粗糙度拟定为房屋比较稀疏的乡镇和城市郊区即B类。

首先是下部结构模型建立，鉴于近年来城市发展，拟选取四种不同层数即7层多层、14层小高层、21层高层和28层超高层钢结构房屋（以下称为下部结构）屋顶建造不同尺寸钢结构广告牌，层高均为3m，长向单跨跨度为6m，短向单跨跨度为5m。

下部结构框架由方钢管混凝土柱与H型钢梁构成，其平面图见图1，图中只表示出6跨，其他跨数下部结构平面布置类似。

图1 下部结构平面图（6跨）

经过试算，各层数下部结构构件均无超限，且观察各模型的基本振型形态均符合标准，以28层的下部结构振型为例，第一振型与第二振型为平动，第三振型以扭转为主变形，第四振型以弯扭为主变形，符合基本振型规律[3]。其他模型亦是如此，由此判断可以进行接下来模态分析。

其次是屋顶广告牌单独结构模型建立，框架体系屋顶广告牌结构采用方钢管支撑体系，主要竖向受力杆件为方钢管□120×4，框架横梁采用方钢管□120×2.5，在框架间加设撑杆采用□60×2和□50×2两种方钢管，各个构件之间以焊接的方式连接。为方便屋顶广告牌两侧支撑与柱最好能支撑在下部结构梁上，最小广告牌（G1）宽度取为三跨共12m其他的广告牌宽度以6m为基数递增，版面分割成方形有利于传力，所以横梁间距取为2m，支座0.5m，则放置于多层房屋上的广告牌G2、G3总高度为4.5m。考虑到广告牌要放置于楼顶，楼层越高越要保证面板尺寸足够大，以便于有良好的展示效果，所以在加宽宽度的同时也要加高，增加一根横梁后高度为6.5m，作为放置于高层以上房屋屋顶的广告牌 G4、G5、G6、G7 高度，广告牌最小尺寸平面图以及立面图见图2，广告牌底部采用全固结型式焊接于各下部结构屋顶，在Midas中单独建立各个尺寸广告牌模型。

最后是建立整体结构模型，广告牌与下部结构钢梁采用固接形式，将广告牌结构分别与对应的下部结构组成一个整体结构，二者之间的尺寸组合见表1。

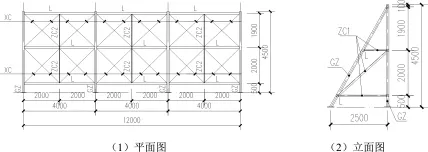
图2 广告牌结构图

2 计算结果及分析

结构的自振周期即结构按基本振型（第一振型）完成一次自由振动所需的时间，从而要得到结构的自振周期就是要研究结构的振动特性[4]。对于一个复杂的振动系统，其固有特性一般包括固有频率和振型，这二者都属于系统的动态特性范畴。且结构的振动特性只取决于结构自身的质量和刚度，模态分析作为动力学分析的基础，使结构动力特性研究更加方便。无阻尼模态分析的基本方程如式1。

整体结构尺寸对应表 表1

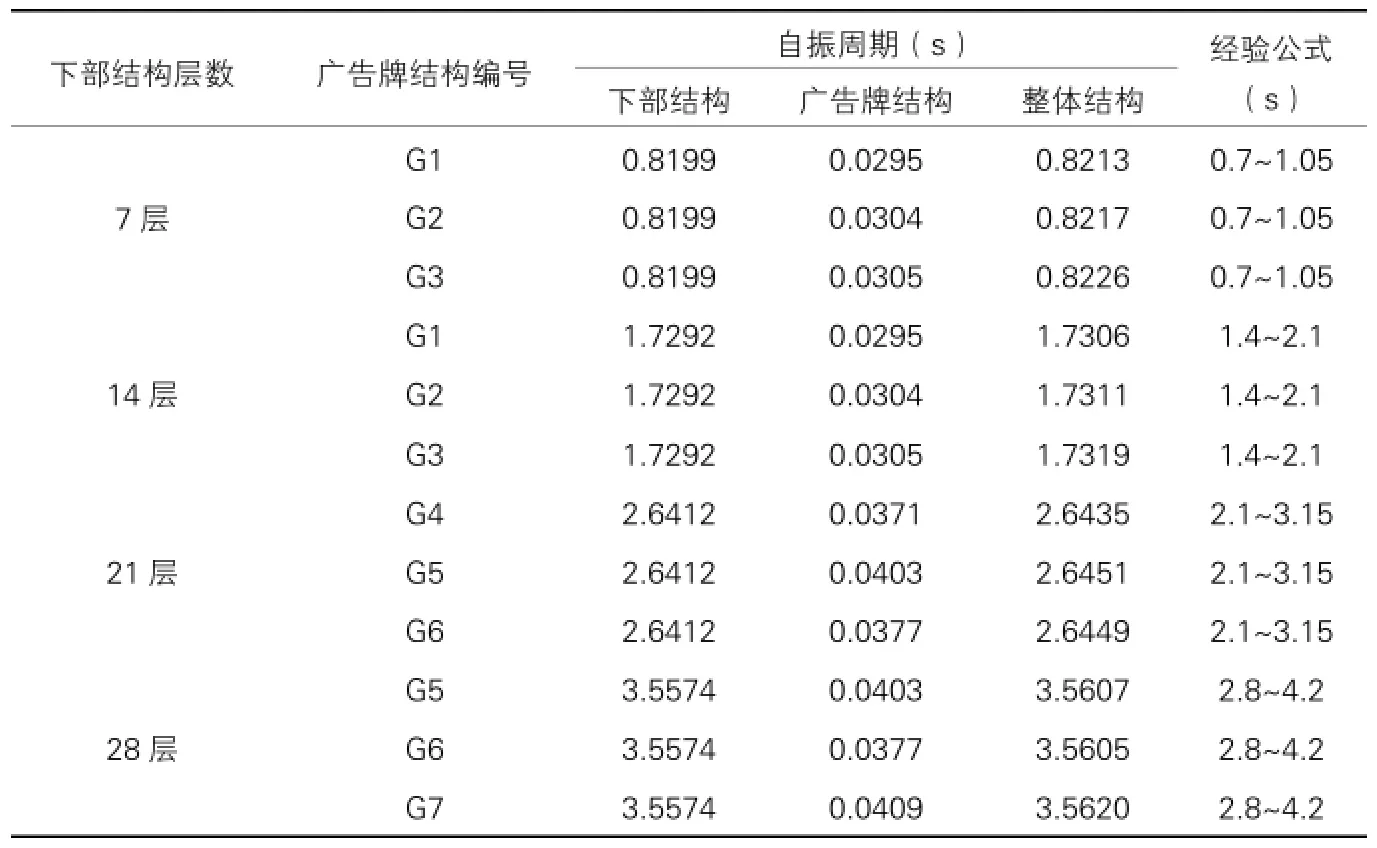
模态分析及经验公式所得自振周期 表2

式中：

[Φi]——第i阶模态的振型向量（特征向量）；

图3 各结构自振周期

[M]——质量矩阵；

[K]——刚度矩阵。

经过Midas软件对上述下部结构、广告牌结构及整体结构进行模态分析，得到各结构第一振型形态和相对应的基本自振周期，选取部分代表性分析结果如图

《荷载规范》规定了一般情况下各种结构的自振周期经验公式，其中钢结构的为T1=(0.10～0.15)n，而钢筋混凝土结构的则为T1=(0.05～0.10)n，其中n为结构的楼层数。为方便比较，本文把上述经验公式计算所得钢结构自振周期也与模态分析所得结果进行对比，得到结果见表2。比较表中数值可知广告牌结构的基本自振周期与整体结构的基本自振周期之间相差很大，有几十倍的差距，当下部结构楼层逐渐增加时相差更加悬殊；而下部结构的基本自振周期与整体结构相比十分接近；并且在对比钢结构经验公式计算结果时，可以发现整体结构的周期都在结果范围内且与范围的中间值十分接近。

分别将表2中所得自振周期带入查表，并按照《户外广告设施钢结构技术规程》相关条款规定风振系数计算公式如式2。

计算各风振系数列入表3，规范中规定在结构的基本自振周期不大于0.25s的情况下，可以对风振影响不作考虑。

式中：

ξ——脉动增大系数；

v——脉动影响系数；

φz——振型系数；

μz——风压高度变化系数。

分析表3可知，就本文建立在多层以上钢结构房屋屋顶的框架体系屋顶广告牌来说，在计算风荷载时不考虑下部结构的影响是有一定危险性的；考虑下部结构所得出的风振系数已经接近单独广告牌结构的两倍，也就意味着考虑下部结构计算所得的风荷载是单独结构的近两倍，这种数值差距是不容忽视的，很显然在计算风荷载时结构基本自振周期只考虑单独广告牌结构是不够安全的，不足以满足结构安全性。同时利用荷载规范中计算钢结构房屋基本自振周期的经验公式所计算得出的中值来计算，风振系数与整体结构计算所得风振系数基本一致，因此在没有条件建立整体结构模型时，可以采用经验公式近似估算广告牌的风振系数。

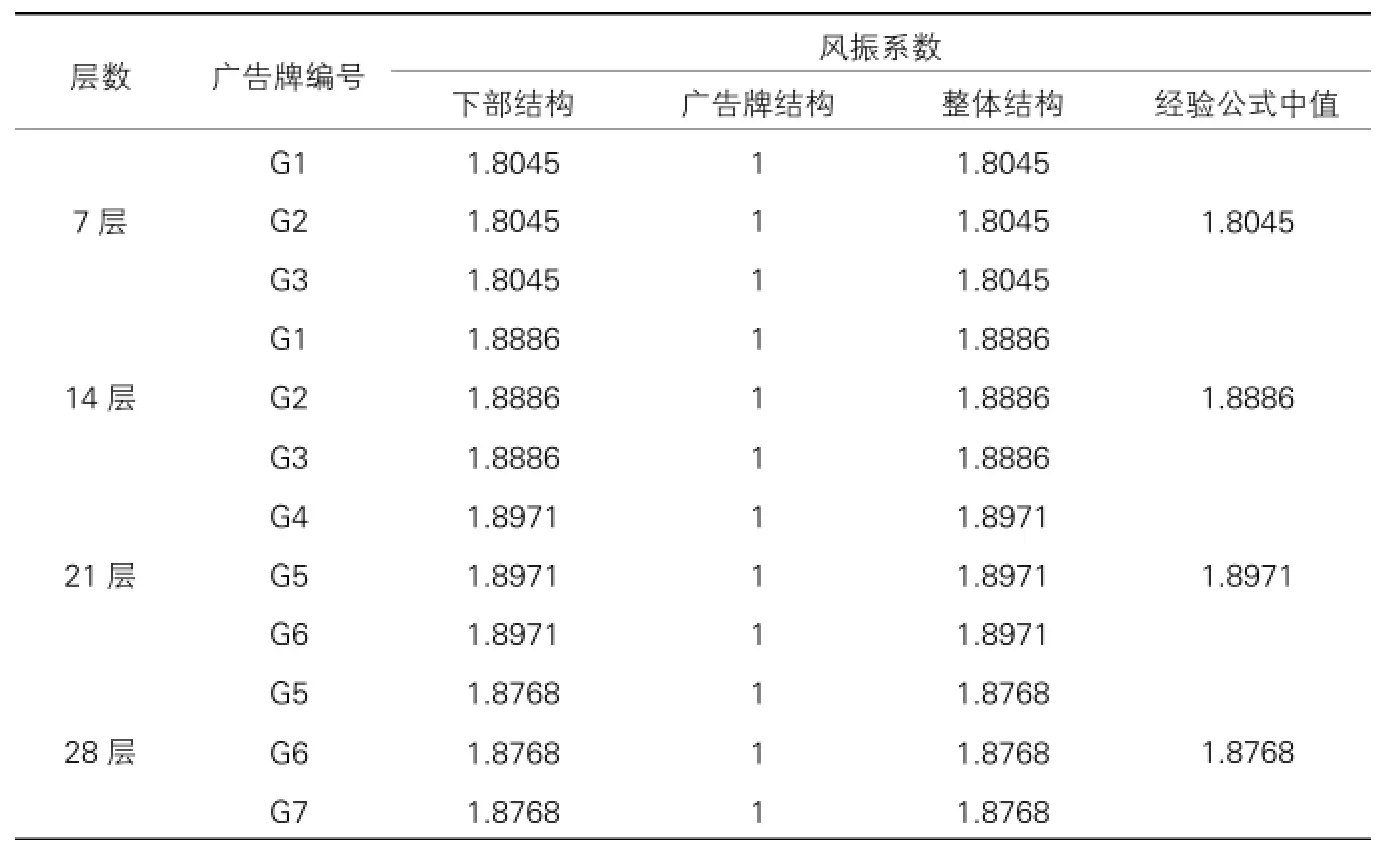
风振系数对比表 表3

3 总结

本文通过建立多个尺寸的下部钢结构房屋、框架体系屋面广告牌与二者结合的整体结构的模型，分析对比其各自的结构基本自振周期，得到结论整体结构的基本自振周期与下部结构的基本自振周期十分接近，并且与单独广告牌结构的周期有巨大差距。并且利用模态分析所得各自基本自振周期来计算广告牌的风振系数，单独广告牌结构计算所得风振系数与整体结构计算所得风振系数要小很多，这样计算出来的风荷载并不安全。由此可得在计算或验算此类屋顶广告牌风荷载时不宜直接用广告牌单独结构来计算，应尽可能地采用整体模型计算，若无法得到整体结构模型则可以根据《建筑结构荷载规范》中规定的房屋基本自振周期经验公式取中值来估算屋顶广告牌结构的风振系数，这样既能减小风荷载计算的误差又方便计算节约时间。对于其他类型的屋顶广告牌结构，也可考虑借鉴此方法使结构计算安全的同时减少计算量。