连续梁桥地震弹塑性反应分析

2020-10-31杨山岗

四川建材 2020年10期

关键词：弹塑性振型抗震

杨山岗

(西安方舟工程咨询有限责任公司，陕西西安 710065)

0 前言

弹塑性分析是桥梁设计领域的重要方法，具体包含静力弹塑性分析和动力弹塑性时程分析两类[1]，前者的模型较为精简，在高度偏小的桥梁中具有适用性；后者可以被应用于绝大部分桥梁工程中，更加接近实际情况，成为现代工程领域较为主流的分析方法。

1 工程概况

南京仙新路过江通道引桥工程跨越长江，全长13.17 km。主线桥梁为城市快速路(荷载兼顾公路I级)，桥面宽26.25 m，设计速度为80 km/h，设计荷载为城-A，为双向6车道，并采用85高程系统，基本抗震烈度为7度，地震动峰值加速度为0.1g，抗震设计工作按安全等级一级标准展开。

2 桥梁结构地震弹塑性反应分析的主要方法

抗震设计是桥梁工程中的重要工作，通过科学的抗震设计方法可以为全桥的设计工作提供重要参考，以便提高桥梁的设计品质，使其建成后可稳定运营[2]。随着桥梁事业的持续发展，抗震设计方法的可选形式较多，此处则对现阶段较主流的三种方法展开分析。

2.1 静力法

静力法作出基本假设，即结构与地震动所具有的振动特性表现出趋同性。地震力的出现具有连锁作用，将随之引发惯性力，取结构总重与地面加速度的乘积，可知惯性力与该结果具有一致性，此时的惯性力则被视为静力，由此展开线弹性地震分析。关于地震力F值可按如下方法求得：

静力法在应用中具有明显的不足之处，其适应性较差，主要原因在于其假定在地震力的作用下结构在任何阶段都维持稳定状态，即不发生变形，但实际情况必然与之存在差异，因此，该假设偏于理想化，仅停留在理论层面。

2.2 反应谱法

相比于其他方法，反应谱法计算简单易懂、计算量较少[3]。通过“地震荷载”理论的指导可以兼顾多方面因素，如自振周期、阻尼动力特性等，从而求得最大地震反应。实际计算中可考虑两种体系。

1)单质点体系。以加速度反应谱和振动周期均是确定值为基本前提，若结构具有规则性，可将其简化为单自由度体系，此时可根据公式求得最大地震惯性力，即：

p=m|δg+ymax|=kHβW

2)多自由度体系。建立在单质点体系的基础上，以设计标准β反应谱为重要基础，经计算后可确定地震力，具体的振动方程有：

[M]{δ}+[C]{δ}+[K]{δ}=-[M][I]δg

式中，[M]、[C]和[K]分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；{δ}为质点对地面的相对位移矢量为时间t的函数。

通过振型的正交性作用，能够实现对联立微分方程的分解，由此得到多个具有独立特性的振动，实现对多质点复杂振动化繁为简的效果，得到各振型{φ}i独立振动的叠加。在此条件下，第j质点水平方向上，由第i振型而产生的地震力上限值可通过如下公式求得：

pji=KHβγiφjiWj

各振型均具有独特性，其最大反应量并非同时发生，因此借助上述公式求解时，应重点分析在不同振型最大值的基础上所形成的组合值，具体求解方式较多，较典型的有SUM法、CQC法等。

2.3 动力时程分析法

动态时程分析法则更具有精细化特性，确定地震动，由此创建有限元动力计算模型，再根据该结果提取振动方程，经过求解后可得到加速度、位移等指标的具体数值。而在结构进入弹塑性阶段后，就需要用该分析法进行抗震的研究和计算。此法分线性动力和非线性动力两种，可更为精准地分析结构抵抗地震力的情况，具体计算方式如下。

1)创建方程并求解。地震动得到完整的记录，以便对结构的运动方程执行积分处理，通过此方式可以得到结构在各个具体时刻所表现出的地震反应情况。关于振动方程如下：

[M]{χ}+[C]{χ}+[K]{χ}=-[M]χg(t)

式中，[M]为结构的质量矩阵；[C]为结构的阻尼矩阵；[K]为结构的刚度矩阵；{χ}为结构的加速度向量；χg(t)为地面运动加速度向量。

多遇地震作用下的时程分析工作中，应考虑到结构处于弹性阶段的特点，此时较为合适的是振型叠加法，即：

[φ]nxq=[{φ1}{φ2}…{φij}]

式中，[φ]为振型贡献率，考虑q阶振型，由此构成n×q阶的振型矩阵，用空间迭代的方式来求出结构阶段周期及相应振型。

2)计算阻尼。以结构的特点为准采取合适的方法，若为均质结构，以瑞丽阻尼矩阵较为合适；对于非均质结构，经验表明以非比例阻尼矩阵为宜。主要元素包含质量m、刚度矩阵k，两者与阻尼具有显著的比例关系，具体有：

c=aοm+a1k

式中，a0、a1为比例常数。

并且，阻尼比与频率的关系有：

根据上式可以得知，对于频率ωm和ωn，在得到各自的阻尼比ξm和ξn后，创建联立方程并求解后便可求得具体的阻比系数值，即a0和a1，以此为依据进一步得到瑞利阻尼矩阵。

2)地震动输入。时程分析过程中，地震波的选择将直接影响最终的分析结果。随着地震波输入值的变化，其对应的地震反应也表现出差异性。通常地震波可选形式分人工地震波、具有代表性的历史强震记录、场地拟建时的地震记录三种。

地震波的加速度峰值应具有合理性，主要考虑的是桥址设防烈度要求的多遇和罕遇地震的加速度峰值，所选值应尽可能与之接近，具体内容有：

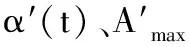
根据本桥的结构特点，将峰值加速度取0.1g，特征周期Tg=0.45s，Ⅲ类场地，阻尼比0.05，在采集到实录地震波后对其加以调整，为El-centro波。通过对公式计算结果的分析后，调整地震波的幅值，得到全新的峰值加速度，最终结果与本桥的0.1g具有高度的相似性。地震波形示意图见图1。

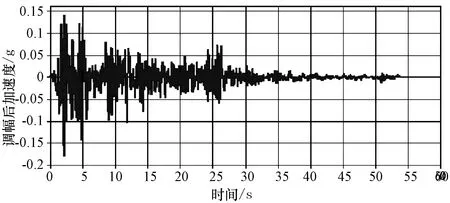
图1 地震波形示意图

3 罕遇地震下的弹塑性分析

强烈地震力作用下结构易出现残余变形，并且处于弹塑性阶段。在此条件下，抗震设计中所采取的弹性设计法缺乏可行性，将其应用于原工程结构有失妥当。对此，在抗震设计工作中则要注重对罕遇地震情况的影响，由此展开弹塑性分析工作，通过此方式有助于提高结构的抗震能力。下文则以钢筋混凝土墩柱结构为例，考虑罕遇地震条件，围绕此时的弹塑性问题展开分析。

3.1 弹塑性动力方程

综合多方面因素，创建弹塑性地震运动方程，具体有：

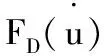
3.2 抗震验算

1)弯矩-曲率关系分析。应用Midas/Civil软件，为便于分析，假定墩结构为屈服状态，在此条件下分析恒载作用对墩底的影响，根据所得的弯矩、曲率参数创建图形，具体结果见图2。从所得结果来看，各墩的弯矩和曲率并无明显的区别，即呈现出趋同性。

图2 墩底弯矩-曲率关系图

2)位移分析。应用Midas/Civil软件，通过该平台展开分析，确定墩顶高的位移量，并进一步与桥墩的容许位移加以对比，评价结构的安全状况。结果表明随着工况的改变，桥墩的墩顶位移具有差异性，主要表现为三向位移，并且各墩虽有变化但幅度相对较小，几乎具有一致性。由此可知，固定墩在变形中发挥出较为显著的承担作用，也正是因为墩承受较大的作用力，因此伴有明显的变形现象。