基于最大剪应力理论的本构模型推导

陈烨开，马雷鸣

(安徽理工大学 土木建筑学院，安徽 淮南 232001)

0 前 言

大量的工程实践表明，地下岩石工程中常发生循环加卸载作用，如道路桥梁等。岩石受到循环加卸载的作用，其力学性质将会产生变化，是影响工程长期稳定性的重要元素，因此，提高岩石稳定性的关键是精确的损伤本构模型。

许多学者在岩石循环加-卸载试验、本构关系等方面都取得了丰硕的研究成果[1-6]。曹文贵等[7-9]研究基于Weibull公式对岩石的损伤模型，将统计强度理论和连续损伤理论结合起来，在岩石本构模型的研究方面得到了重大进展。

本文根据岩石微元强度理论服从最大剪应力理论，从Weibull 随机分布的特点出发，建立出能够表现出分等级加卸载的本构模型。由于本构模型中代表岩石的微元强度的参数包含损伤变量，致使损伤变量中包含损伤变量使得本构无法拟合，本文对本构模型进行等式变换，消去岩石微元强度和损伤变量表达式中的损伤变量，进一步把本构关系变换成简单的幂函数，弥补了非线性曲线拟合初值不易选取的缺点。

1 岩石本构模型

1.1 本构模型的建立

依据Lemaitre理论[1]，得出岩石损伤本构模型的基本关系式为：

(1)

假设微元的总数为N，发生破坏的微元数为N1,定义损伤变量D为N1与N的比值。D的范围为0～1，D为0时未发生破坏，D为1时岩石完全破坏。根据 Weibull 分布损伤变量D的表达式为[9]：

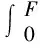
(2)

1.2 微元强度的确定

目前，岩石力学研究中采用多种表现形式的破坏准则，曹文贵等[9]以Drucker-Prager、Coulomb-Mohr作为岩石的强度准则,这种研究方法有参数物理意义明确优点，但岩石在复杂应力状态下的性状研究的不够，这些理论不能无条件地适用。在单向试验中，试件表面出现了与杆轴大约成45°角的斜线。因为最大剪应力发生在与杆轴成45°角的斜面上，这些条纹是材料内部晶格间的相对剪切的结果。一般认为这种晶格的错动是产生塑性变形的根本原因，得出最大剪应力决定材料的破坏。最大剪应力准则这一理论对于解决塑性岩石的问题给出了满意的结果，笔者确定了基于最大剪应力破坏准则的岩石微元强度为：

(3)

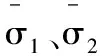
1.3 单轴作用下岩石本构关系

天然材料的岩石内部存在着一定的先期损伤，其内部强度并不完全相同，而是呈随机分布。损伤力学认为岩石材料在加载过程中，损伤是一个连续的过程，做出以下假设。

1)假设岩石断裂前是线弹性体。

2)岩石材料服从各向同性假设。

3)假设岩石各微元破坏服从Weibull分布，其概率密度函数为[9]：

(4)

式中，F为岩石的微元强度；F0与岩石平均宏观强度有关，m与岩石微元分布集中程度有关，反映了岩石材料的力学性质。将式(4)代入式(1)、(2)可得单轴加卸载损伤本构模型为:

(5)

(6)

(7)

(8)

B=F0An

(9)

2 结 论

假设岩石微元强度服从最大剪应力理论和微元破坏服从Weibull的概率公式，建立一种能够描述岩石在循环加卸载状态下的本构模型，对本构的等式变换消去损伤变量和岩石微元强度表达式里的损伤变量，得到采用应力、应变、弹性模量等参数表示的关于损伤变量和岩石宏观强度的表达式。

[ID:010288]