追本溯源，源于“思维”自然生长

蹇雯媛

摘  要：根据北师大版小学数学教材编排，从一年级下册开始，学生就正式学习加减法竖式计算了，到二年级下册学习三位数加减法竖式计算，整整经历了一年半的学习时间，在此之间，学生对竖式计算方法已经滚瓜烂熟，“相同数位对齐，从个位算起，相加满十向前一位进一，相减不够向前一位借一作十。”但是，为什么要从个位算起？学生并没有认真思考过，只是将“从个位算起”作为计算的规定执行，同时教师在平时教学中也没有重视“从个位算起”必要性的解释，只是把它当做刚性的规定。本文将从教材编排，编者意图，学情分析等几个方面进行阐述“从个位算起”的必要性，同时设计相关教学环节，落实“从个位算起”必要性的体会。

关键词：竖式计算;从个位算起;连续进位;连续退位

竖式本质是一种计算工具，它将计算过程进行简洁而有效的记录，体现化繁为简的数学思想。从一年级下册开始，孩子们就接触加减法竖式计算了，到二年级下册学习完三位数加减法竖式后，已经整整经历了一年半的学习时间，在此之间，孩子们对竖式计算方法已经滚瓜烂熟，张嘴就来：“相同数位对齐，从个位算起，相加满十向前一位进一，相减不够向前一位借一作十。”那为什么还要对“三位数加减法竖式计算”的算理进行梳理与回顾呢？本人是基于以下几方面来思考的：

一、教材编排情况

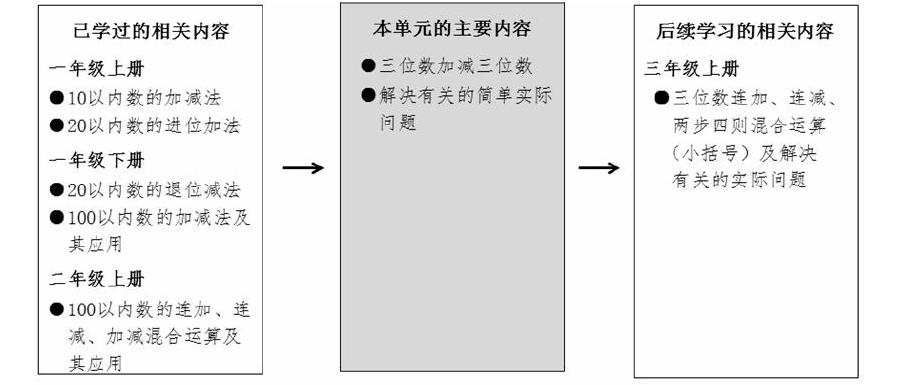
北师大版教科书关于整数加减法运算的学习分为了四个层次，采取了螺旋上升的编排方式：

“第一个阶段是10以内数的加减法，内容安排在一年级上册第三单元，重点是学习不进位、不退位的加减法。第二个阶段是20以内数的加减法，内容分布在一年级上册第七单元和一年级下册第一单元，重点是学习进位加和退位减。第三个阶段是100以内数的加减法，内容分布在一年级下册第四单元和第六单元。第四个阶段是三位数加减法，内容分布在二年级下册第五单元和三年级上册第三单元。”

综上所述，可以看出二年级下册第五单元是关于整数加减法竖式计算学习的最后一个阶段。后期，教材没有再对加减法竖式计算的计算方法进行阐述，在此时，学生理清算理，掌握算法显得尤为重要。随着学习的渐进，数域的扩大，计算也会更加多样化，难度也会增加。此阶段学生是否形成扎实的计算能力，将直接影响后续的学习效果。为了引导学生“回顾→梳理→思考→质疑”，从而真正内化掌握，在此阶段有必要做一个小结，有意识地引导和培养学生建立加减法竖式计算的体系模型，为后续学习打下良好的计算基础。

二、研读编者意图

教师用书在教学建议中对“从个位算起”孩子们如何有层层递进的体验，是有详细教学建议的。孩子们第一次学习用竖式计算出现在一年级下册《拔萝卜》一课，即两位数加两位数（不进位加法），教参第134页中说到“至于从个位还是十位开始加，在这里没有明显的优越性，教师可以提倡从个位加起。为后面的学习埋下伏筆。至于为什么要从个位加起，可以提出这个问题，并告诉学生在接下来的学习中揭开这个谜底。”同样，在两位数减两位数（不退位减法），教参第138页中说到“减的时候是从个位开始减还是从十位开始减呢？这里没有明显的优越性，教师可以提倡从个位减，至于为什么要先从个位减，也可以提出这个问题，到后面学习退位减法时再进一步讨论。”综上所述，在不进位不退位的加减法中，因为没有明显的优越性，从个位算起只是提倡，也并没有解释从个位算起这样做的原因。让学生思考为什么要从个位算起，感受从个位算起的方便性则放在了进位加和退位减的教学中。最早出现在一年纪下册《图书馆》一课，即两位数加一位数（进位加法），教参第162页中说到“竖式计算时从哪一位开始方便？你有什么体会？”同样，在《跳绳》一课，即两位数减两位数（退位减法）时教参第177页中说到“在竖式中为什么要从个位开始减，你有什么体会？”

由以上分析得出，教材编写者重视让孩子们体会“从个位算起”的优越性。但是，在这之前学习的两位数进位加和退位减，数据较小，从个位算起的优越性不是特别明显，孩子们对于“从个位算起”这个道理也只是停留在初步感知层面上，体会不深刻。同时，我们在课堂教学中也没有重视“从个位算起”优越性的解释，而是把它变成了一种刚性的规定。现在到了二年级下册，学习三位数的进位加和退位减，数据较大，特别是有连续进位加和连续退位减时，从个位算起的优越性才显得更加突出了。因此我们有必要带领孩子们在这个阶段进行三位数加减法竖式计算的巩固与强化，并且可以用“竖式计算从个位算起”为话题，展开三位数加减法竖式计算复习课。

三、学生学习情况分析

二年级下册学生学习了三位数与三位数之间的不进位加，进位加，连续进位加;不退位减，退位减和连续退位减的竖式计算。再加上一年级下册和二年级上册对竖式计算的学习，孩子们已经有相当丰富的经验来正确进行竖式计算了。可是落到笔头上，我们发现竖式计算全对率仍然很难达到100%。学习完二年级下册三位数加减法竖式计算的知识后，在全年级进行了竖式计算专项测试，学生完成情况如下：

通过对学生竖式计算错误类型的收集，发现三位数连续进位加和连续退位减，特别是带“0”的时候，错误率极高。针对这部分孩子进行询问时，他们又能说清楚算理和算法，那么导致这样高的错误率出现，本人认为问题出在了孩子的审题能力上。低段孩子学习加减法的计算尚且要出现这类问题，随着年级不断升高，数域扩大，乘除法计算以及混合运算的加入，往后的计算正确率更难以掌控，所以很有必要进行竖式计算的专项复习课，为孩子们打下扎实的计算基础。

四、精心设计教学环节，突破算理本质理解。

1.创设情境，设置冲突，引发质疑。

复习课开始时可以用话题引入：“竖式计算时可以不从个位算起吗？”结果全部同学都不同意这个说法，通过询问得知，学生认为“从个位算起”是规定，从学竖式计算时老师就这样要求了，怎么可以不从个位算起呢？由此可见，学生并没有深入思考为什么从个位算起，只是单纯认为这是规定。

针对这样的情况，我们可以开展第一轮计算PK，以不进位加法和不退位减法的竖式计算为例，分男女生两个战队进行对比计算练习，女生不从个位算起，男生从个位算起。结果学生发现不从个位算起也能算得又对又快，于是引发部分学生心里对“从个位算起”这个规定产生质疑。有孩子开始认为不从个位算起也是可以的了，其实这正是学生个性化思考的结果，沿着老师设计的问题开始真正思考为什么从个位算起了。当然更多的孩子选择坚持原来的判断，因为他们知道竖式计算还有进位加和退位减的类型，不从个位算就会很麻烦。

2. 验证质疑，感受优势，肯定规定，说清算理。

不从个位算到底麻不麻烦呢？实践出真理，于是接着展开第二轮计算PK，对比计算连续进位加和连续退位减。考虑这是复习课又是低段的孩子，应该将核心学习内容尽量放在较短的时间内完成，所以可以跳过进位加和退位减直接进行连续进位加和连续退位减的练习。

这次计算要求全班同学都不从个位算起，切身体会不从个位算起很麻烦，还容易算错。接着适时对学生进行询问，他们的感受就很真实了，原来不从个位算起真的很麻烦。最后全班同学再按照从个位算起的方法进行第三次计算，深刻体会从个位算起的便捷性，同时结合算理，理清了相加满十向前一位进一，相减不够向前一位借一作十。正是这样的学习真正展示了孩子们习得知识的过程，学生们经历认定→质疑→反思→再认知，反反复复，将所学知识进行更迭与优化，通过思维的分享、碰撞、提升，最终才找到了正确的方向。

3.培养学生大胆质疑的思维品质

对于“培养学生大胆质疑的思维品质”如何在教学中落实，我们可以用问题模式进行路径培养。在第一次不进位加和不退位减计算PK后，有孩子开始认为不从个位算起也是可以的了，于是我们可以询问这些孩子：对于从个位算起这样的规定，你有什么想问的吗？于是学生大胆说出心中的想法：“一定要从个位算起吗？”“还可以从其他数位算起吗？”在低段教学中，用“一定要…？”“还可以…？”这样两个疑问句型能够帮助孩子們表达内心的疑惑，随着年龄增加，知识储备越来越丰富，孩子们能提出的质疑问题也就越来越多。但是低段的孩子需要我们老师给这样一根“拐棍”，扶一扶。当然，大家也可以根据自己的语言习惯，选择适合的话语问题，在教学中落实培养质疑的思维品质。

4.回扣话题，拓展提升。

有基础也应有提升，在最后一个环节，我们可以设计两道竖字谜类型的题目。

例：

对这两道题目，孩子们首先应该进行题型判断，第一道是连续进位加，第二道是连续退位减。接着通过对题目的分析，发现第一道加法竖式从个位入手算起比较方便，然而第二道减法竖式的个位无法确定，只能从别的数位入手算起。至此，再次加深孩子们对“从个位算起”必要性的体会，因为它方便，让计算有序，也不容易算错，但是当从个位计算无法解答时，也可以从其他数位入手。学习到此，孩子们的体会也更深刻，对于不进位加不退位减，从不从个位算起均不影响计算结果;对于进位加退位减，从个位算起才更方便;对于数字迷一类的计算，则根据分析，哪一位方便就从哪一位算起。至此，学生的学习形成闭环。

五、反思感悟

通过对“从个位算起”这一规定的详细解读，我对竖式计算知识构架有了全方位的理解，对教学的本质也从懵懂变得清晰。反思自己平时的教学，很多时候并没有像这样去深入思考一句话、一个表述对学生正面或负面的影响。教学时容易将一些法则和规定作为刚性要求让学生掌握，而忽略了学生们的学习体会。

教学没有完美的，教育也不是一潭死水，它是流动的，灵动的，发展的。如果我们深入研究，严谨思考，准确表达，将学习的要求转变成学生的一种意识，我们的教学就成功一大半了。思考永无尽头，研究永无止境，相信这就是教学研究的魅力！

参考文献

[1]  义务教育教科书数学教师教学用书.北京师范大学出版社.一年级下册.二年级下册.2013

[2]  竖式计算真的简单吗？谭柳.教育视界.2016（20）.

[3]  浅谈竖式的价值体现.杨艳林.小学教育.2017（01）.