基于多元线性回归的“拍照赚钱”任务定价方案

古静

摘 要：“拍照赚钱”是如今互联网下的一种自助服务模式，而APP中的任务定价又是核心的要素。本文对定价规律进行分析，再对每个任务的定价情况与影响因子进行回归分析，建立了基于多元线性回归的定价模型。

关键词：拍照赚钱;任务定价;多元线性回归;

一、定价规律分析

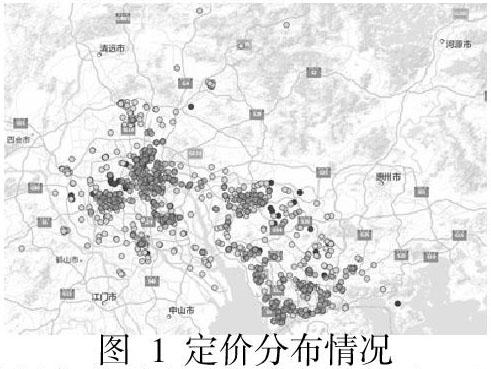
结合附件一的数据按照价格区间进行分类后，绘制出任务点的定价空间分布图，如下图所示：

图中，五种颜色分别表示的价格区间为：蓝色[65，69]、绿色（69，73]、黄色（73，77]、紫色（77，81]、红色（81，85]。通过观察可以看出，这些点围绕在中心点的附近，越靠近中心点的价格较低，远离中心点的价格较高。

从任务点与会员位置两个角度来分析，得到5个定价因素，并将这5个因素分别与任务定价作回归分析，从而得到它们的显著性如下表所示：

如上表所示，可知偏僻程度、任务密度、会员密度、任务限额的显著性值皆小于0.05，则可判断这四种因素与任务标价的相关性十分强，而信誉值的显著性值大于0.05，与任务标价的相关性较弱，则不纳入计算之中。

二、基于多元线性规划的定价模型

1、模型的建立

现设任务定价由三部分组成：

其中为固定低价，即任务的最低价格，我们在对定价进行分析后，取最低价65元作为，表示赏金，即在任务和会员位置分布影响下的浮动价格，λ为受不确定因素影响（如天气、交通管制等）的价格浮动，由于数据有限，可認为λ的影响较小，故暂不讨论。

（1）记为任务的偏僻程度

是任务点所属区域的中心点，是离中心点最远的任务点，为该点距中心点的距离，为最远点距中心点的距离，且该点离中心点越远则越偏僻。

（2）记为会员密度

其中为以任务点为中心，为半径的圆形区域中会员的个数。

（3）记为任务密度

为以任务点j为中心，为半径的圆形区域中的任务个数。

（4）记为区域内会员的限额密度

n为圆域内会员总数，为第i名会员的限额数量。则：

由于λ暂不讨论，因此找到和的值后可得到定价公式，即任务定价规律模型如下：

解出定价模型后，再将任务未完成的数据代入此公式算出相应参数，并分析定价模型的参数与未完成任务的参数，从而判断任务定价高低的合理性。

2、模型的求解

当显著性P值小于0.05时，我们认为线性回归模型通过了检验，同时证明得出的结果有效。系数计算结果如下图所示：

故任务定价规律如下：

三、结束语

“拍照赚钱”任务定价主要是由任务偏僻程度以及会员密度、任务密度、区域内会员的限额密度决定的。故可以根据各影响因子与定价之间的关系建立模型，从而求得任务的最终定价。本文“拍照赚钱”的定价模型对各省份均适用。

参考文献

[1] 王惠文，孟洁.多元线性回归的预测建模方法[J].北京航空航天大学学报，2007

[2] 王璐.带线性约束的多元线性回归模型的统计诊断 [D].南京理工大学，2008

[3] 韩中庚.数学建模方法及其应用[M].高等教育出版社，2009.