基于奥斯本检核表法：构建高中物理课堂问题设置的方法

唐小明

摘 要：一切课堂活动主要围绕着教师所设置问题而有序地展开的。本文从7个方面阐述了运用奥斯本检核表法构建课堂教学问题设置的一些方法，以解决物理教学中的主干知识教学，提升物理教学质量与学生综合素养。

关键词：奥斯本检核表法;构建方法;问题设置

奥斯本检核表法是指以该技法的发明者奥斯本命名、诱导主体在创制经过中对照7个方面的题目实行思考，以便启迪思绪、开垦思想想象的空间、鼓舞人们出现新联想、新计划的方法。分类和举例如下：

1.缩小突出主题

课堂问题与教学目标紧密关联，问题设置应有明确地指向，要紧贴教学重点，这是高质量问题必须具备的首要特征。为此，设置问题时应尽量缩小涵盖，具体化，否则问题的提出就无法突出主题，给学生一种“盲人骑瞎马—不知奔向何方”的感觉。

如讲授“动力学的两类问题”课堂教学过程中，我们将会有许多知识结合在一起，如受力分析、运动学公式、多个过程等等，如果我们将其要点缩小到中心点“加速度”上，让学生围绕“加速度”左右突破，彻底解决无从下手这一难关。

如：一个静止在水平地面上的物体，质量是 2kg，在 6.4N的水平拉力作用下沿水平地面向右运动。物体与地面间的摩擦力是4.2N。求物体在4s末的速度和4s内的位移。

一旦学生能认识这类习题“动力学的两类问题”的特点，便让学生从“加速度”直扑主题，引导学生走受力之路，还是走运动学公式之路，目标明确下尽快地进入思维状态。使动力学的两类问题有一个快速解决之法，可见，教师设置问题时应质问自己“问题是否可以缩小，力求清晰，课堂教学针对性强。

2.扩大引向开放

有问题才能给学生思维方向，有效问题才会激起思考与探索，我们积极倡导问题具体化与提出开放性问题不会产生矛盾，具体化问题可以走向开放，也只有具体化才会有开放思路。大家都知道，问题越大，解决问题就会越复杂，学生的思考空间就会越大;问题越小，解决问题的方法就会越简单。问题过于浅显，学生的思考余地就小，不能反映思维的深度，同样，问题过于深奥，学生不知所云，不能引发学生积极地思考。

3.颠倒换位思考

设置问题时要替学生着想，问题难度要建立在学生认知水平和已有的经验基础之上，使“最近发展区”转化为“现实发展区”，以帮助学生的智力与能力协调发展。合理的课堂提问能创设师生互动、互惠的教学关系。因此，教师设计合理的问题，能使学生在课堂中乐学、学会，促进师生间相互交流，增进了解。好的提问方式能促使学生内容丰富的语言输出、能促进学生较多地参与课堂活动、能增进师生、生生之间使用目标语进行交流。

例如长直木板的上表面的一端放有一个木块，如图2所示，木板由水平位置缓慢向上转动（即木板与地面的夹角α变大），另一端不动，则木块受到的摩擦力Ff随角度α的变化图象是下列图3中的（）

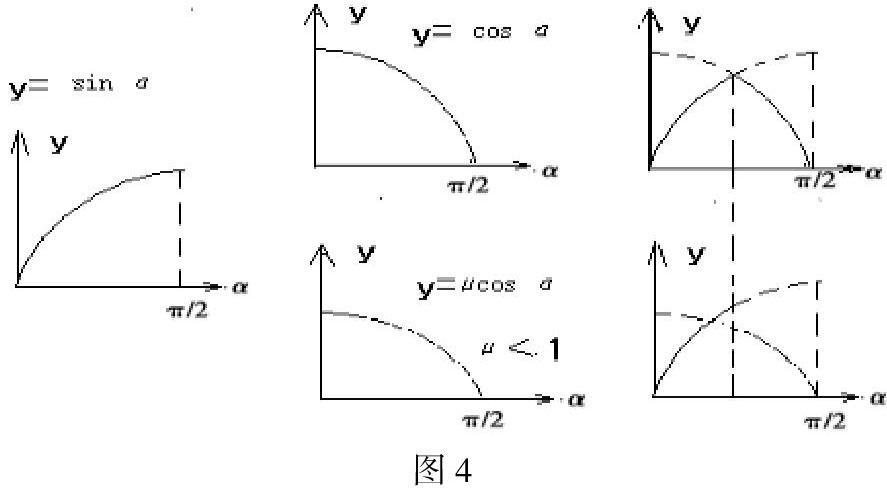
作为教师来说，发现答案中是由两部分组成的，知道静摩擦力与滑动静摩擦力受力分析，很简单入题解决。若站在学生立场上，物理的受力分析与数学函数相結合就需要铺设台阶，我们可让学生画一画正弦与余弦函数，然后再进行受力分析，得到Ff静=mgsin α.及Ff滑=μmgcos α，在这里我们不妨再让学生思考画出Ff滑=mgcos α。来找出Ff滑=μmgcos α与Ff滑=mgcos α，相似之处与不同之处，最后我们将图象进行组合如图4，就可得到结论为C。

学生根据图象进行分析，

得出“先拆分、后组合”的解题规律之后，再引导解答上述问题就显得轻松自如了。当然我们同学可能有更精彩的解法。

如特殊位置法，本题选两个特殊位置也可方便地求解，具体分析见下表：

特殊位置 分析过程

木板刚开始运动时 此时木块与木板无摩擦，即Ff静=0，故A选项错误.

木块相对于木板刚好要滑动而没滑动时 木块此时所受的静摩擦力为最大静摩擦力，且大于刚开始运动时所受的滑动摩擦力，即Ffm>Ff滑，故B、D错误.

由以上分析知，选项C正确.

4.重整化解难点

对于同一类问题应从多层次，多方位加以剖析，要在原有知识基础上提炼升华，把常规思路和解题方法重新整合，以崭新面貌呈现给学生，启发新思路，探索新解法，让学生感到内容新颖，学有所思，思有所得。象高三复习“牛顿运动定律在直线中的应用”是教学重点，也是难点，许多教师采取分类设置大量习题的方法，试图让学生在强化训练中掌握各类解题技巧，但收效甚微。若将这些习题进行有效整合，其效果迥然不同。

如图5所示，一质量为m的木块以初速度v滑上斜面。在整个运动过程中，斜面处于静止状态。已知斜面的质量为M，倾角为θ，木块与斜面间的动摩擦因数为μ。求，

（1）木块在斜面上的最大位移为多少。

（2）如果小木块能回到斜面底端，则其滑行的总时间为多少。

若让小木块带正电，电量为q，且斜面倾角为θ=30ˉ，则：

（3）小木块沿斜面加速往下滑的过程中，加一范围足够大的竖直向上的匀强电场，电场强度E=mg/q，小木块将如何运动？

（4）小木块沿斜面加速往下滑的过程中，加一范围足够大的竖直向下的匀强电场，电场强度E=mg/q，小木块将如何运动？

（5）小木块沿斜面加速往下滑的过程中，加一范围足够大的匀强磁场，磁场方向垂直与纸面向外，磁感应强度为B，小木块在斜面上将如何运动？

由此你能得出什么样的解题规律？”这样整合之后，便于教师引导而可得出“受力分析、匀变速直线运动规律、牛顿运动定律是最基本最常规的解题途径，其中加速度是桥梁，是纽带，同时动能定理也可解题”等解题规律，有效地化解了教学难点。

5.改变激发兴趣

由于教材与教辅资料的导向作用，教师设置问题往往出现固定模式，学生觉得枯燥无趣，在复习课中显得更加突出。如我们经常看到下一类复习问题：

杭州市政府为实施城市形象工程，从20世纪90年代开始实行楼房平改坡工程，即把原有楼房的平顶改造为有坡度的斜屋顶。如图7所示为一跨度为L的楼顶，现需要在上面加一个坡顶，①是60°、45°、30°吗？②如何加最合适？请说出你的理由。

由此看来，教师从学生实际出发，精心组织教材，把陈旧的课堂问题做必要改变或包装，给学生以 “新鲜感”，使之产生兴奋，提振精神，活躍思维，并通过“再认识”，“再研究”，“再归纳”深化理解。

6.组合构建体系

要上好一节物理课，单靠一两个提问是不够的，它需要教者站在高处，整节课、从整个教学内容体系来谋划，设计出一组有计划、有步骤的系统化的问题，这样的提问才有一定的思维深度，才能从多方位培养学生的思维能力。在教学中，对于那些具体有一定深度难度的内容，学生难以一下子理解、领悟，可以采用化整为零、化难为易办法，把一些太复杂的问题设计成一组有层次、有梯度的问题，以降低问难度。

例如，学习了“动能和动能定理”一节动能的概念后，多数教师热衷于设置多个问题，逐一击破，可事与愿违。若考虑组合，按一定的逻辑关系形成下列“问题串”，将会大大提升问题质量。能起到有效引领学生展开总结提炼、反思升华的作用。

问题1：动能是矢量还是标量？ 我们应如何来计算一个物体动能的变化量？

问题2：一个运动员骑自行车绕圆形的赛道以大小不变的速度行驶，那么在运动的过程中，运动员的速度变不变？他和自行车的动能变不变？

问题3：一个质量为2Kg的物体以大小为4m/s的初速度沿水平地面向东作匀减速运动，经过一段时间后其速度方向变为向西，且大小也为4m/s，则此过程中物体的速度大小变化量为多大？物体的动能变化量又为多大？

问题4：一个小孩以大小为4m/s的初速度，水平地把一个质量为0.2Kg的沙包抛出，经过0.3s沙包落地，你能求出沙包落地时动能吗？

这4个问题，由浅入深，相辅相成，构成了一个可以促进学生学习概念、理解概念、应用概念的“问题串”，可以看出，解决“问题串”过程，将会使学生的知识结构化、系统化，模块化，避免泛泛而谈，匆匆而过，增加了学生内化知识的机会。

7.借用激起探究

课堂设置问题有助于引发学生的认知冲突，给学生在心理上造成一种困惑，驱使学生积极主动地进行知识的回忆与建构，诱发学生进行信息的收集活动和探索行为，帮助学生在探索新知识的过程中产生新的问题意识。同时学生在不断地分析问题、解决问题的过程中，逐渐地将知识内化，形成自己的“见识”和“观点”，并且思维能力逐渐得到提高，只有助于学生提出高水平的问题。所以，教师要科学合理利用课堂所设置问题，通过引发学生的认知冲突，发展学生的思维能力，促进学生有效地发现和探究问题。

总之，基于奥斯本检核表法，构建问题设置的方法，一定要反复自问：哪些可有？哪些可无？哪些模糊？哪些有效？哪些多余？哪些改进？毫不犹豫地剔除低质高负的问题，会让问题问出“精彩”、让小问题创造出“大智慧”、让课堂教学充满活力。

参考文献

[1] 普通高中物理课程标准. 人民教育出版社，2019.

[2] 周锦秀.新课程校本教研问题与指导. 陕西师范大学出版社，2005.

[3] 张飞翔.高三物理课堂问题设计之管见.陕西大学出版社，2011.