一道几何题的多样解题思路与延伸思考

2020-10-30陈希陈彦军

科学导报·学术 2020年42期

关键词：数学

陈希陈彦军

摘要：本文从不同角度对一道平行四边形的几何题目进行了证明，并延伸思考，增加特定的题设，研究其结论。最后借助数学绘图软件，从函数角度去探究题目中几何图形面积之间的关系。

关键词：数学，几何题，多样解题思路。

1 题目再现

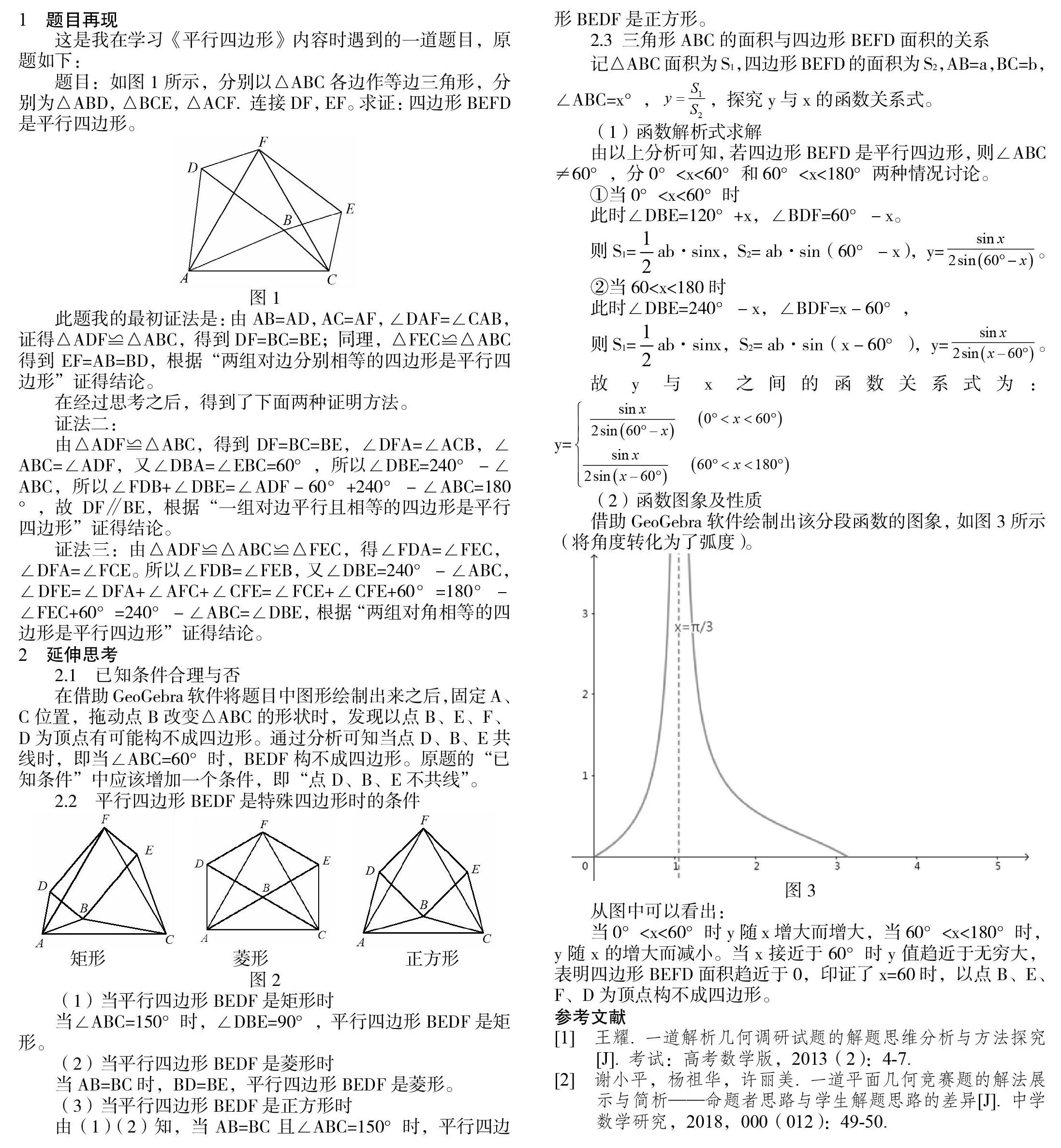
这是我在学习《平行四边形》内容时遇到的一道题目，原题如下：

题目：如图1所示，分别以△ABC各边作等边三角形，分别为△ABD，△BCE，△ACF. 连接DF，EF。求证：四边形BEFD是平行四边形。

此题我的最初证法是：由AB=AD，AC=AF，∠DAF=∠CAB，证得△ADF≌△ABC，得到DF=BC=BE;同理，△FEC≌△ABC得到EF=AB=BD，根据“两组对边分别相等的四边形是平行四边形”证得结论。

在经过思考之后，得到了下面两种证明方法。

证法二：

由△ADF≌△ABC，得到DF=BC=BE，∠DFA=∠ACB，∠ABC=∠ADF，又∠DBA=∠EBC=60°，所以∠DBE=240°-∠ABC，所以∠FDB+∠DBE=∠ADF-60°+240°-∠ABC=180°，故DF∥BE，根据“一组对边平行且相等的四边形是平行四边形”证得结论。

证法三：由△ADF≌△ABC≌△FEC，得∠FDA=∠FEC，∠DFA=∠FCE。所以∠FDB=∠FEB，又∠DBE=240°-∠ABC，∠DFE=∠DFA+∠AFC+∠CFE=∠FCE+∠CFE+60°=180°-∠FEC+60°=240°-∠ABC=∠DBE，根据“两组对角相等的四边形是平行四边形”证得结论。

2 延伸思考

2.1 已知条件合理与否

在借助GeoGebra软件将题目中图形绘制出来之后，固定A、C位置，拖动点B改变△ABC的形状时，发现以点B、E、F、D为顶点有可能构不成四边形。通过分析可知当点D、B、E共线时，即当∠ABC=60°时，BEDF构不成四边形。原题的“已知条件”中應该增加一个条件，即“点D、B、E不共线”。

2.2 平行四边形BEDF是特殊四边形时的条件

（1）当平行四边形BEDF是矩形时

当∠ABC=150°时，∠DBE=90°，平行四边形BEDF是矩形。

（2）当平行四边形BEDF是菱形时

当AB=BC时，BD=BE，平行四边形BEDF是菱形。

（3）当平行四边形BEDF是正方形时

由（1）（2）知，当AB=BC且∠ABC=150°时，平行四边形BEDF是正方形。

2.3 三角形ABC的面积与四边形BEFD面积的关系

记△ABC面积为S1，四边形BEFD的面积为S2，AB=a，BC=b，∠ABC=x°，，探究y与x的函数关系式。