斜轴投影在公路勘察设计基础控制网建立中的应用探讨

（甘肃省交通规划勘察设计院股份有限公司，甘肃 兰州 730030）

近年来，我国高速公路建设快速发展。受地形等客观条件的限制，公路设计中出现越来越多的特大桥梁、隧道等构造物，根据《公路勘测规范》《公路勘测细则》等规范要求，控制网的精度依不同等级要求须分别达到四等1/35000、三等1/70000、二等1/100000。为了控制投影变形，投影时一般选择任意带高斯抵偿投影，如果在不考虑高程对投影变形影响的前提下，要保证控制网精度高于1/100000，测区东西最多能控制20多公里。而对于某些东西走向长达上百公里甚至更长的高速公路，如果按照传统的高斯投影方式进行投影计算，势必进行分区投影，产生多个工程坐标系，给设计、施工带来诸多不变。本文提出沿公路走向选取中央子午线，采用斜轴等角切圆柱投影，利用墨卡托投影的原理方法对公路控制网工程坐标进行求取，并通过实例验证其较传统高斯投影的优越性。

1 高斯投影变形

1.1 高斯投影变形计算

高斯投影属于等角投影，在投影前后角度元素保持不变，能很好保持与实际地面图形相似。但对于长度元素，高斯投影存在一定程度的变形，主要源自两个方面。

1）由地面投影到参考椭球面上的变形

假设某两点平均高程为Hm，水平距离为Sm，R为平均曲率半径，则地面两点之间的水平长度归算到参考椭球面所产生变形的近似值，用公式（1）计算：

2）由椭球面到高斯平面上的投影变形

假设某两点的横坐标平均值为Ym，参考椭球面上的长度投影到高斯平面上所产生变形的近似值，用式（2）计算：

由以上公式可知，影响高斯投影变形的因素主要是地面点到投影椭球面的垂向距离（H）及偏离中央子午线的距离（Y）。因此，实际工程应用中一般通过选取合理的投影面和中央子午线来控制投影变形。

1.2 控制高斯投影变形的措施

1.2.1 消除地面投影到参考椭球面上的变形

根据公式（1）可知，此项变形中只需使Hm尽可能小即可达到目的，故选取投影面时一般以测区平均高程面作为投影面。

1.2.2 消除高斯投影变形

根据公式（2）可知，此项变形影响因素为Ym，选取时一般以测区平均中子午线作为中央子午线。

1.2.3 采用任意带抵偿投影消除变形

公式（1）的变形值为负，公式（2）的变形值为正，二者共同影响总投影变形，故综合考虑使：

即：

进行高斯计算时，选取合理的投影面和中央子午线，使公式（4）成立。

2 斜轴墨卡托投影

采用墨卡托投影确定投影球体时,通常做法是以与地面最贴近的椭球体半径R构建圆球体，让投影圆柱与该圆球体相切，切线即为投影中线，其投影前后长度保持不变，而距离投影中线越远的地方变形越增加。

2.1 投影球体的确定

假设测区中心某点P0，其在WGS-84中的大地坐标为（B0、L0），测区平均高程为H0，则确定该基点p0（B0，L0，H0），令投影球体的在P0点处的径向与WGS-84椭球在该点处的法线重合，使测区地面点尽可能位于球面上。设投影中线的大地方位角为A0，该点处的子午圈半径为M0，卯酉圈半径为N0，则该新球体的半径为：

2.2 建立球体坐标系框架

以球心指向P0点方向为X’轴，过P0点与沿A0方向形成的圆面为新赤道面，过P0点与新赤道面垂直的面为该点处的子午面。则Z’轴为经过球心与赤道面垂直的方向，与Y’轴共同构成新球体的左手空间直角坐标系，故p0点在该坐标系中的坐标为（R0,0,0）。

令p0点在WGS-84椭球中的空间直角坐标为（X0,Y0,Z0）,则有：

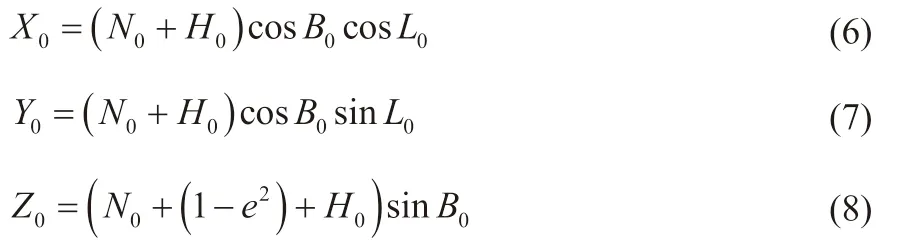
以P0点在GGS-84椭球和新建椭球中的空间直角坐标系为转换条件，求取其余待求点在新椭球下的空间直角坐标：

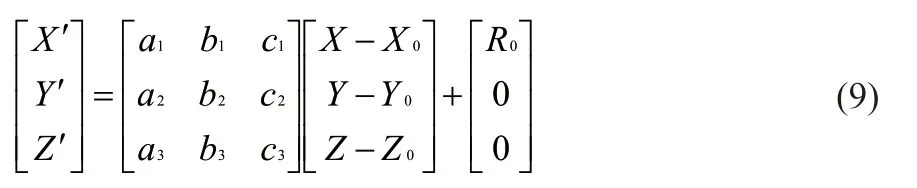
式中：

X,Y,Z为待求点在WGS-84椭球下的空间直角坐标

2.3 新建球体下的待求点大地坐标

构建新椭球时尽管使球体球面与实际地面尽可能吻合，但由于地形起伏变化，其中一部分点并未贴在球面上。在地形较平坦的测区，选择合适的球体半径就能很好控制高程投影带来的变形；但对于起伏较大、范围较广的区域，为了控制变形，将各点沿垂线方向投影到新建球体表面，一般情况下利用法线方向代替垂线方向。

各控制点在新建椭球下的高程为:

在充分估计H’对投影变形的影响后，各控制点在新建椭球下的空间直角坐标为:

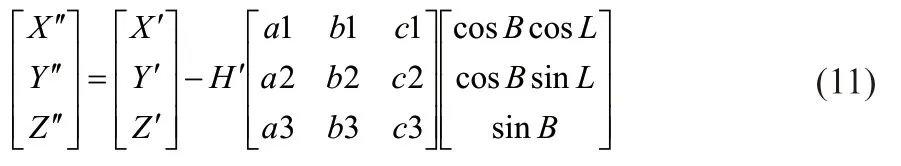
根据修正后的各点空间直角坐标成果，即可求得各点在新建椭球下的大地坐标:

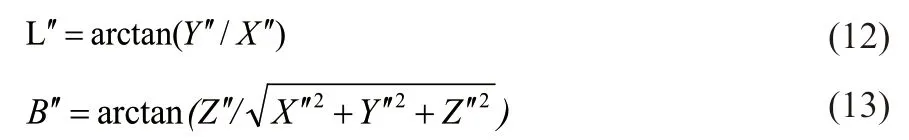
2.4 投影坐标

本文讨论的是根据斜轴墨卡托投影原理，为了控制从球面到投影变形，将柱面沿测区中线展开，以新建椭球的赤道线位X轴，以初子午线为Y轴，采用等角投影原理，故有：

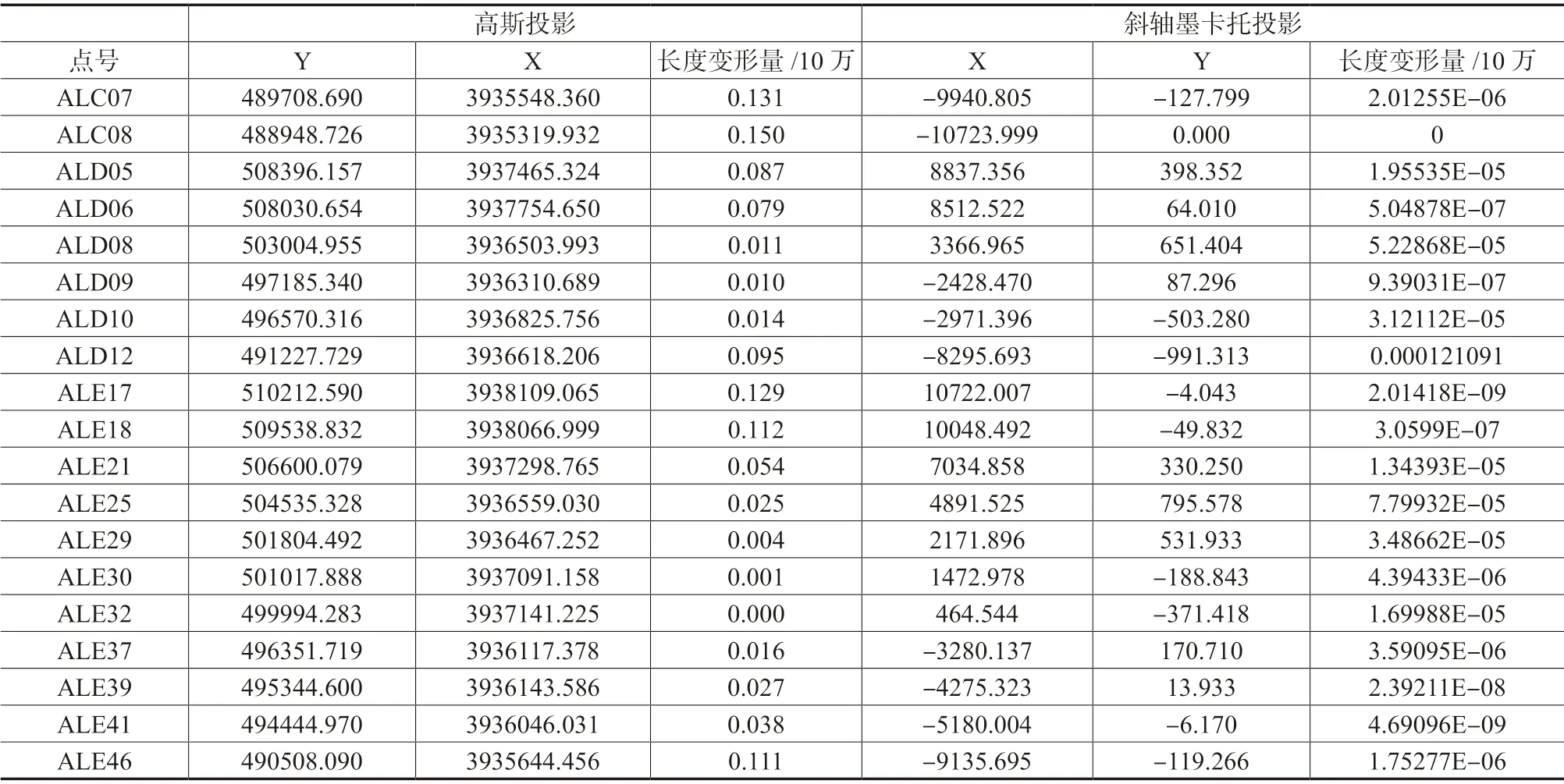
表1 某线路部分控制点两种投影结果比较

3 案例应用

在实际工程应用中，高斯投影变形主要源于两个方面：一是投影到椭球面上产生的变形，主要影响因素为实际地面到椭球面的高差；二是由椭球面归算到高斯面上产生的变形，主要影响因素是偏离中央经线的距离。本文主要讨论斜轴墨卡托投影的优越性，故选取的工程案例是呈东西走向、高差变化较小的带状测区，且在求取投影变形的过程中仅考虑上述第二类变形。

案例中中心线走向方位角为82°31′，新建椭球半径为6380132.5549米。按上述公式计算结果见表1。

从表1可以得出：

1）斜轴墨卡托投影同高斯投影的投影方法一致，都采用等角投影，保证投影前后角度不变形，仅存在尺度变化。

2）通过比对，斜轴墨卡托投影较高斯投影在控制长度变形量方面有明显的优越性。

3）表中Y值的绝对值越大，变形量越大，故在选择中心线时尽可能使各点距离中心线距离较小。

4 结语

东西走向的带状测区采用斜轴墨卡托投影可以很好地减少投影带来的长度变形，若斜轴投影坐标与设计坐标不一致，可通过三参数转换来实现，不影响变形。