灰色-支持向量回归模型在多应力加速寿命试验寿命预测中的应用∗

葛 峰 韩建立 高 松，3

（1.海军航空大学 烟台 264001）（2.92419部队 兴城 125106）（3.91115部队 舟山 316000）

1 引言

加速模型是正确反映产品寿命与各环境应力之间数学关系的关键，当利用加速寿命试验获取的产品失效数据预测产品寿命时，通常采取利用加速模型来推测计算的方法，从而得到目标应力作用下的产品寿命，对于多应力条件下加速模型的建立，当前通常采取参考常用的单应力加速模型进行复合的方式建模[1]，如广义艾林模型、Peck模型、通用对数模型等。这种方式建模通常忽略掉应力之间的耦合作用，认为各应力之间相互独立、互不影响，且在建模过程中选取合适的单应力模型要求研究人员具有较高的先验知识水平[2]。同时鉴于多应力条件下产品失效模式多样、失效机理复杂，通常难以获得泛化性好、预测精度高的模型。本文探索基于灰色-支持向量回归（GSVR）的加速模型，研究思路见图1，并与单纯地支持向量回归（SVR）模型比较，用以验证模型实际效果。

2 模型的建立

2.1 灰色理论原理

灰色理论由我国邓聚龙教授在1982年提出，主要研究贫信息及不确定性的理论。灰色建模中包含三个基本过程：累加生成操作（AGO）、灰色建模以及逆累加生成操作（IAGO）。若有n维原始数据列x(0)=[x(0)(1)，x(0)(2 )，...，x(0)(n)]，若对x(0)进行如下计算：

此过程即为累加生成操作（AGO），称x(1)=[x(1)(1)，x(1)(2 )，...，x(1)(n)]为原始序列的AGO生成序列。反之，由x(1)到x(0)的过程则称之为逆累加生成操作（IAO）[3]。

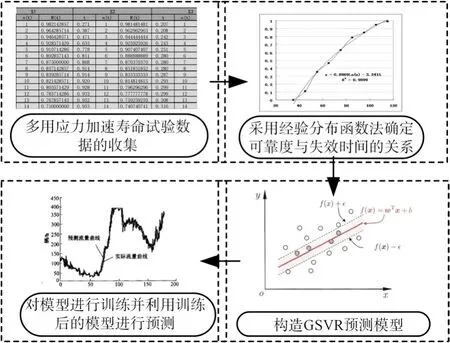
图1 GSVR多应力加速模型研究思路

GM（1，1）是最简单且在当下应用最为广阔的模型。根据灰色理论，一个n维数据列x的级比σ(k)=x(k-1)/x(k)必须要落在区间内，才能作有效的灰色建模。若未能落入区间内，则要进行适当的变换处理，常用的变换处理方法主要是对数处理、方根处理、平移处理，累加生成操作是灰色信息挖掘、建立模型的一个关键步骤。

2.2 支持向量回归简介

支持向量机理论由Vapnik等在1995年首先提出，该算法在面对小样本、非线性及高维情况下的识别问题中显示了独特的优势。SVM以结构风险最小化代替经验风险最小化，能够避免过学习、维数灾难、局部极小等传统机器算法中存在的问题，在小样本条件下仍具备较好的泛化能力。支持向量机还利用核函数映射解决了高维情况，算法复杂度与样本维数无关。在模式识别、回归分析、时间序列预测等领域得到了广泛的应用[4]。

利用支持向量机进行回归预测需引入不敏感损失函数ε，用以控制拟合精度，若预测值与实际值之间的差别小于ε，则损失为0[5]。其表达式为

对于既定训练数据，利用线性函数f(x)=(w·x)+b对其进行拟合，以式（2）为损失函数，则转化成了对回归的支持向量估计，根据最优化理论结合拉格朗日乘子法，最终可得决策函数为[6]

2.3 灰色-支持向量回归多应力加速模型的建立

1）多应力加速寿命试验的数据收集与处理。收集每组多应力水平下产品失效时间，使用经验分布函数法计算得到相应多应力条件下产品失效时间和可靠度之间的关系。

2）失效时间及可靠度的级比检验及累加生成。对各应力水平下的产品失效时间序列t和可靠度序列R进行级比检验，若不满足条件则进行方根处理直至满足级比检验，而后进行累加生成操作得到t′，R′。

3）将处理后的试验数据确定训练集、测试集。训练集用于后续SVR模型的训练，测试集用于后续SVR模型预测及检验。

4）建立支持向量回归模型并进行训练。对训练集各组应力水平及t′，R′分别进行归一化处理后，以各应力水平和R′为输入向量，t′为输出向量。在Matlab2014平台下采用Labsvm软件包中svmtrain函数对模型进行训练，选用径向基核函数，经过训练获得预测模型。

5）利用训练后的模型开展预测。采用测试集中应力水平及R′为输入向量，利用训练后的预测模型采用Labsvm软件包中svmpredict函数进行预测，对预测所得失效时间进行逆归一化和逆累加生成操作从而得到还原后的失效时间t[7]。

6）预测结果的评价与检验。选择评价参数指标，对预测的失效时间与测试集中真正的失效时间进行比较检验，对模型的预测效果进行验证评价。GSVR模型建模及预测流程见图2。

3 实例应用

3.1 试验数据的来源

根据查国清等文献[8]中智能电表在三应力（温度、湿度、电应力）加速寿命试验中的结果数据，使用经验分布函数法，计算获得相应多应力条件下产品失效时间与可靠度之间的关系。

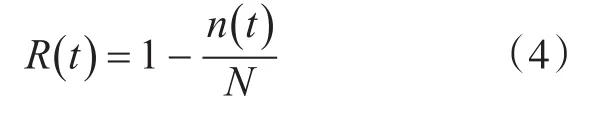
其中，R(t)为t时刻的可靠度，n(t)为t时刻故障的智能电表数量，N为该条件下智能电表总数量。用式（4）可计算获得每个应力条件下智能电表可靠度与失效时间的关系，以试验中S1应力条件下计算结果为例，具体情况见表1，其余应力条件下的数据计算同理。

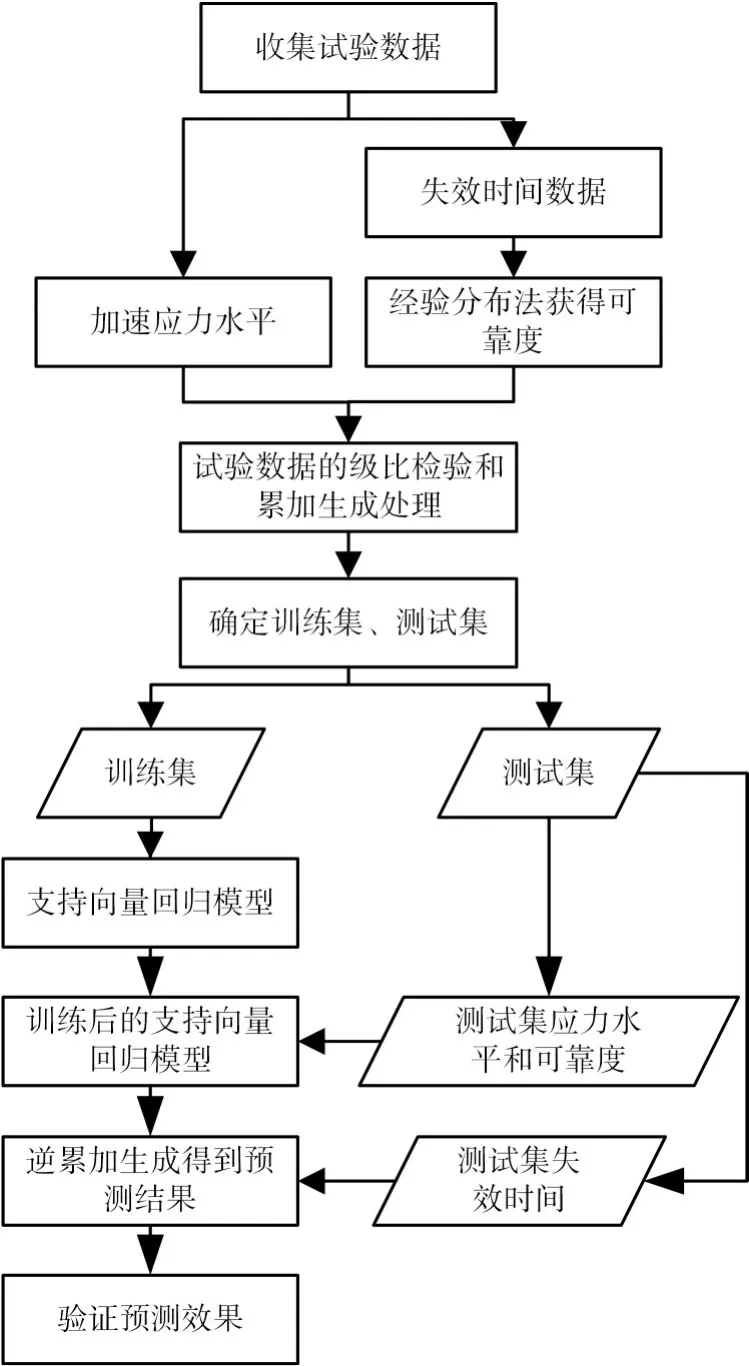
图2 GSVR模型建模及预测流程

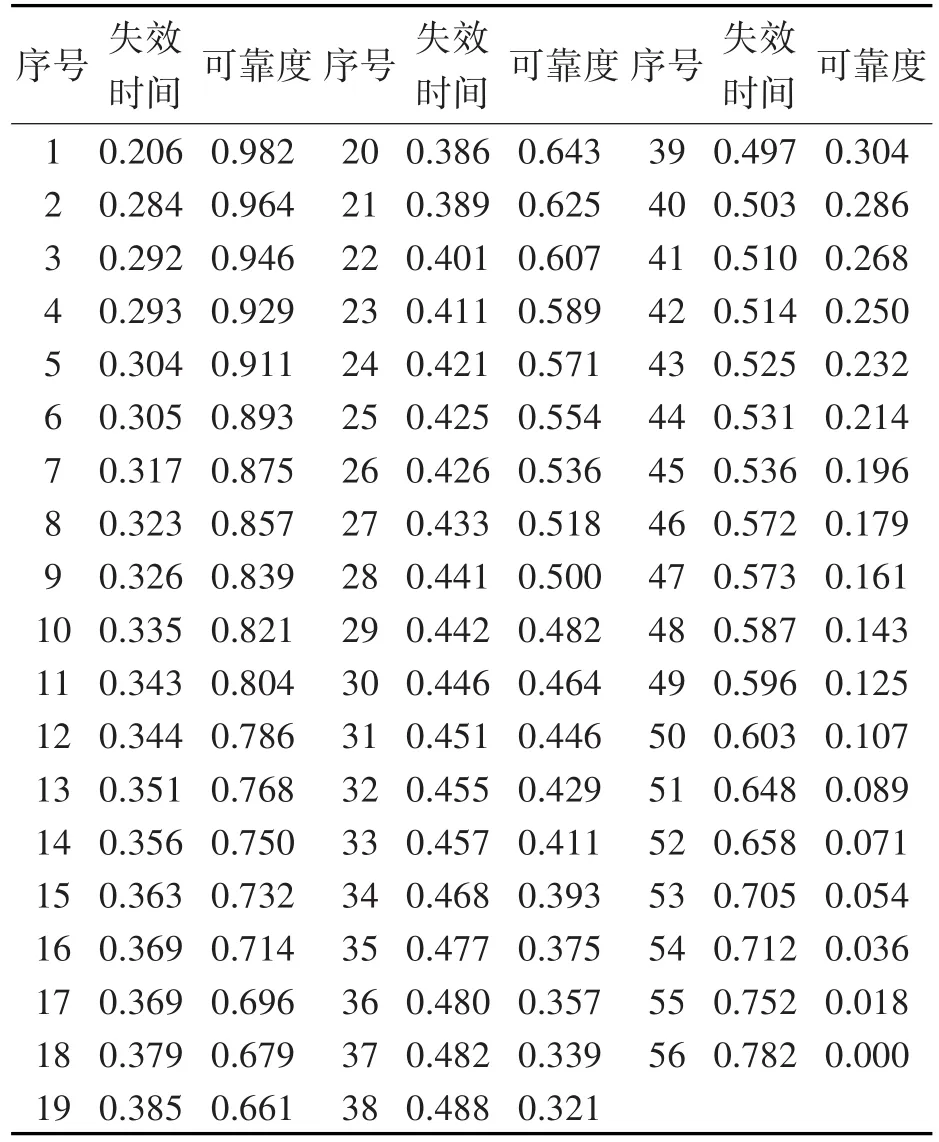
表1 S1应力水平下智能电表可靠度与失效时间对应情况

3.2 GSVR与SVR模型的预测效果比较

为检验模型的应用效果，本节利用相对误差Re、平均相对误差Are、拟合优度Cod等参数作为评价指标[9]。其公式如下：

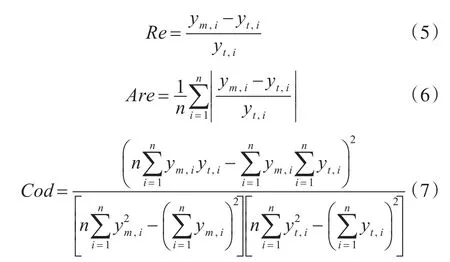
式中：n为样本数量；ym，i(i=1，2，…，n)为第i个样本的模型预测值；yt，i(i=1，2，…，n)为第i个样本的真实值。

使用 S1、S2、S3、S4应力水平作用下的数据分别对GSVR、SVR模型进行训练，而后分别利用训练后的GSVR、SVR模型对S5应力水平下寿命进行预测，两个模型预测结果见图3，相对误差情况见图4。

图3 GSVR与SVR模型预测情况

从图3、图4可以看出相较于SVR模型，GSVR模型的预测效果较好，相对误差基本在0.1之内；SVR模型在中后段的预测相对误差较大。可以看出相较于SVR模型，GSVR模型预测及拟合效果更好，在预测性能上有了较好的提高。GSVR、SVR模型Are、Cod比较结果见表2。

图4 GSVR与SVR模型预测相对误差情况

表2 GSVR、SVR预测模型预测效果对比

4 结语

本文探索了GSVR模型在多应力加速试验寿命预测中的应用，通过与SVR模型预测效果的比较，验证了模型较好的预测效果和良好的泛化性。与传统的物理加速模型相比较，本模型具备以下突出特点：1）模型泛化性好，适用性强，不需要获取具体的加速模型和产品的失效机理等信息对研究人员的先验知识的要求更加友好；2）建立模型简单，通过对试验数据进行灰色累加生成和支持向量回归学习训练即可开展预测，避免了求解多元似然方程组等困难，同时模型预测精度满足工程需求[10]；3）该模型原理上属于基于机器学习的非参数多应力加速模型，随着机器学习算法的发展和计算机技术的发展，该类模型将有更加广阔的发展空间[11]。