基于EWM-BN的空中来袭目标威胁评估∗

（火箭军工程大学 西安 710025）

1 引言

目前国内外对威胁评估（Threat Assessment，TA）都展开了一定研究，常用的方法主要有多属性决策[1～2]、神经网络[3～5]、贝叶斯网络[6～7]、模糊理论[8～9]等。来袭目标威胁评估即要考虑定量因素，又要考虑定性因素。本文采用一种并行处理的思路：基于EWM对定量指标进行处理，减少定量指标权重向量的确定中主观因素的影响；基于BN对定性指标进行处理，充分利用BN对不确定性问题进行推理的优势；合理选择合适的线性加权因子，得出综合威胁度。

2 威胁评估指标分析

2.1 指标选取

来袭目标的威胁程度受多种因素的影响，获取影响因素的信息越多，对于其威胁程度的评估越准确，但是在实际作战过程中，敌我双方基于战场生存的需要开展空地电子战等各种斗争，我方能获取的来袭目标信息量十分有限，而且防空作战对于评估的实时性要求比较高，因此需要综合考虑我方雷达性能和侦查手段，科学选取敌方来袭兵器的威胁评估指标，构建合理的指标评估体系。对于评估指标的选取，目前尚未统一意见，本文综合参考文献[10～11]，主要选取目标类型、作战意图、干扰能力、作战能力、速度、高度、进入角、距离8个指标。

2.2 指标处理

指标处理主要是对定量指标的处理，由于雷达提供的定量指标的量纲、数量级等都存在较大差异，应该对各项定量指标进行无量纲处理，主要是采用隶属度函数将各属性值处理成区间[0，1]内的实数。具体方法如下：

1）速度：随着来袭目标飞行速度的加快，其对我方保卫目标的威胁程度就越大，反之则其对我方保卫目标的威胁程度越小。目前，武装直升机的飞行速度一般不超过0.2Ma，而战斗机的飞行速度可达3 Ma左右，加之雷达跟踪发现敌机的性能以及武器装备的性能有限，为了更科学地对不同类型目标的速度进行归一化处理，将速度大于3Ma的数值量化为1，将速度小于0.2Ma的数值量化为0.2，其余数值选择上升型的隶属度函数，表示为

其中，速度v的单位为km。

2）高度：来袭目标飞行高度越低，更利于其隐蔽突防，其威胁度就越大，因此选用降半正态分布函数作为隶属度函数进行归一化处理。当目标高度小于1km时，其隐蔽突防和规避机动的能力非常强，设定此时其对应隶属度值为1，因此隶属度函数表示为

其中，高度h单位为km。

3）进入角：进入角是以来袭目标和我方保卫目标连线为基准，与来袭目标飞行方向形成的夹角，顺时针方向为正，逆时针方向为负，其取值处于[-180°，180°]范围。当取值在[-90°，90°]范围内时，进入角绝对值越小，对我方保卫目标威胁度也越大；当取值超出[-90°，90°]范围，取值为0。因此选取中间型函数作为隶属度函数，表示形式为

其中，进入角单位为°。

4）距离：来袭目标距离我方保卫目标的距离越近，其对我保卫目标威胁度更大，此选用下降型函数作为隶属度函数进行归一化处理。当来袭目标距离小于10km时，其对我方保卫目标的威胁是致命的，此时其对应隶属度值为1，因此隶属度函数表示为

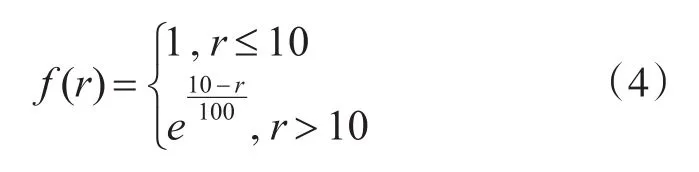
其中，距离r的单位为km。

3 基于EWM-BN的威胁评估方法

3.1 构建评估模型

基于EWM-BN的来袭目标威胁评估方法主要采取的是并行处理的思路，具体实现方法为：基于EWM对来袭目标的各定量指标构成的目标属性矩阵进行处理，确定在动态威胁度计算中各定量指标的权重系数，得出目标动态威胁度；构建静态威胁度和来袭目标各定性指标BN网络，推理得出目标静态威胁度；根据实际情况选择合适的线性加权系数，对动态威胁度和静态威胁度进行加权得到综合威胁度，根据需要对来袭目标进行威胁度排名。威胁评估框图如图1所示。

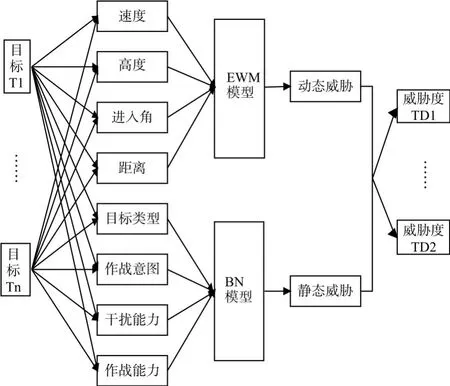
图1 基于EWM-BN的威胁评估框架

3.2 基于EWM的动态威胁评估

熵原本是一热力学概念，最先由C.E.Shannon引入信息论，称之为信息熵。在信息论中，如果某个指标的熵值越小，说明其指标值变异程度越大，提供的信息量越多，在综合评价中该指标起的作用就越大，其权重就越大。因此，基于EWM的动态威胁评估客观性更强[13]，能够更好地解释得到的结果。其具体评估步骤如下[13]：

1）将获得的定量指标进行隶属度处理后，构造来袭目标的动态威胁度属性矩阵A=(aij)m×n，aij为动态威胁度第i个目标在第j个指标下的隶属度。

2）对动态威胁度属性矩阵A进行归一化处理，得到归一化属性矩阵B=(bij)m×n，其中，则各属性熵值可以表示为

3）计算各定量属性权值，其权值表示为

4）构造权重矩阵，根据属性矩阵与权重矩阵计算出各目标的动态威胁度TDm。

3.3 基于BN的静态威胁评估

来袭目标静态威胁评估共包含四个定性指标，即目标类型、作战意图、干扰能力、作战能力，构建静态威胁评估模型如图2。

图2 静态威胁度评估模型

图2中各节点状态如下：

1）静态威胁度（Static Threat Degree，TDs）：根据程度大小区分为高、中、低。

2）目标类型（Type，T）：主要区分为大型机、小型机、直升机。

3）作战意图（Operational Intention，OI）：主要区分为轰炸、攻击、侦查。

4）干扰能力（Interference Ability，IA）：主要区分为强、中、弱。

5）作战能力（Combat Capability，CC）：主要区分为强、中、弱。

构建好评估模型后，需要进行参数学习。参数的获得主要有样本学习和专家经验两种途径，本文采用专家经验进行学习获得相应节点的条件概率表。根节点静态威胁度预先无法获得任何信息，先验概率可表示为P(TDs)=(0.33，0.34，0.33)。条件概率表如表1。

构建好贝叶斯网络后，主要利用贝叶斯推理公式得到静态威胁度各状态的概率值P（高，中，低），公式如下：

定义静态威胁度各状态（高，中，低）的期望值为（0.9，0.5，0.1），则可求得静态威胁度的值：

3.4 综合威胁度计算

用加权因子δ表示动态威胁度在综合威胁度中的权重，则(1-δ)表示静态威胁度的权重，对两者进行线性加权即可得到综合威胁度，公式如下：

若δ＞0.5则表示综合威胁度的评估过程中定量指标比较重要，反之，则定性指标比较重要，本文取δ=0.5。

表1 静态威胁度评估节点条件概率表

表2 来袭目标属性参数

4 仿真分析

假设在某次防空作战中，某一时刻我方侦察系统获得来袭目标的属性参数如表2所示。本方法在Matlab2014a和Netica 5.18软件下运行，计算可得各来袭目标的威胁度，如表3所示。

由结果可知，空中来袭综合威胁度排序为：目标4＞目标2＞目标3＞目标6＞目标5＞目标1＞目标8＞目标7。在动态威胁度分析中，根据定量指标权向量可知，来袭目标速度越快、距离越近、攻击意图越明显（进入角越小），则威胁度越大；而在静态威胁度分析中，来袭目标作战意图和类型对威胁度的影响相对比较重要，符合战场实际情况和先验知识。因此，根据动态威胁度和静态威胁度的偏好情况，选取合适的加权因子，通过线性加权可以得出的综合威胁度更加科学合理。

表3 来袭目标的威胁度评估

5 结语

来袭目标威胁评估即要考虑定量因素，又要考虑定性因素。本文采用一种并行处理的思路：基于EWM对定量指标进行处理，减少定量指标权重向量的确定中主观因素的影响；基于BN对定性指标进行处理，充分利用BN对不确定性问题进行推理的优势；合理选择合适的线性加权因子，得出综合威胁度。最后通过仿真实验，得出结果符合战场实际情况和先验知识，验证了基于EWM-BN开展来袭目标威胁评估切实可行。