基于积分滑模的搜索雷达方位控制算法研究∗

（中国船舶重工集团公司第七二三研究所 扬州 225101）

1 引言

雷达技术发展迅速，软件化、通用化等新概念雷达的提出，对雷达伺服系统控制性能要求越来越高[1～2]。作为搜索雷达重要组成部分的伺服系统，控制技术是制约雷达系统探测性能的关键之一。

目前雷达伺服系统的控制策略仍然以传统PID控制算法为主。PID算法虽然简单可靠，但其参数整定过程繁琐，局限于线性系统，鲁棒性差，对于非线性系统以及外部干扰效果较差[3]。雷达方位伺服控制系统主要考虑风力矩、惯性力矩、不平衡力矩及摩擦力矩等，惯性力矩、摩擦力矩对于特定对象保持不变，不平衡力矩及风力矩与实时工作环境及设备姿态有关，具有时变非线性的特性。因此，单一的PID控制已无法满足雷达新技术研究和发展的需求。

滑模控制的本质是非线性，其非线性表现为控制的不连续性，对外部扰动不敏感，具有良好的抑制外部扰动的能力。为改善雷达伺服系统的控制性能，提高系统的稳定性和鲁棒性，提出一种积分滑模控制算法。在详细分析了雷达伺服系统动力学特性的基础上，建立雷达伺服系统的数学模型，基于模型设计一种积分滑模控制策略，利用滑模控制不受外界干扰的特性提高控制系统抗干扰能力和稳定精度[4～6]。仿真结果显示，相对于传统的PID控制算法，设计的积分滑模控制算法具有更好的系统稳定性，控制精度和抗干扰能力。

2 雷达伺服系统数学模型

雷达伺服系统内部传动机构的具体传递函数比较复杂，为了简化设计，将伺服控制单元与天线负载结合在一起看作是被控对象，建立雷达数学模型，进行控制算法研究。建立模型时将电机及驱动器（电流环、速度环、逆变器）假设为理想状态，整个伺服系统简化为电机模块、减速器以及天线座机械部分，建模过程中不考虑天线座机械结构以及减速器造成的延迟，雷达伺服系统简化为一个带负载（天线及减速器）的永磁同步电机模型。雷达伺服系统的数学模型可近似为带负载的永磁同步电机的运动方程。

永磁同步电机数学模型：

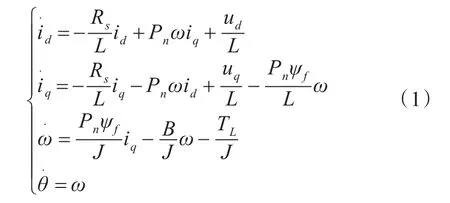
雷达伺服系统的数学模型：

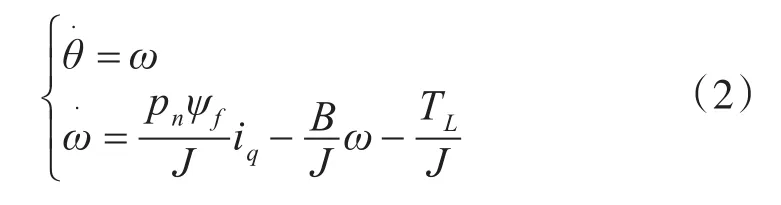
式中：TL为系统负载，包括电机转矩和天线机械结构的等效负载转矩，B为摩擦系数，包括天线不对称力矩造成的摩擦。

3 雷达伺服系统滑模控制策略

基于积分滑模控制算法的雷达伺服控制系统原理框图如图1所示，主要包括电流环、速度环、位置环三个部分，电流环及速度环由高性能的电机及驱动器集成，可以有效抑制电机、非线性和反电动势的影响。位置环设计积分滑模控制算法，抑制负载扰动的影响，实现伺服系统快速稳定的运行。

3.1 积分滑模控制器设计

定义误差方程：

式中：θ*是设定角度，θ是实际角度。

图1 伺服控制框图

由式（1）可得：

定义积分滑模面：

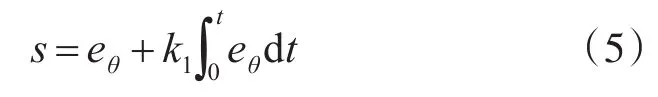
式中：k1为积分系数，取大于零的常数。

定义滑模控制率：

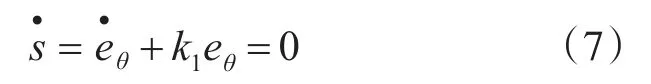
将式（3）代入式（7）得到等效控制律：

切换控制律选择常值切换函数：

式中：λ＞0。

3.2 稳定性证明

选择李亚普诺夫函数：

将式（10）关于时间求导：

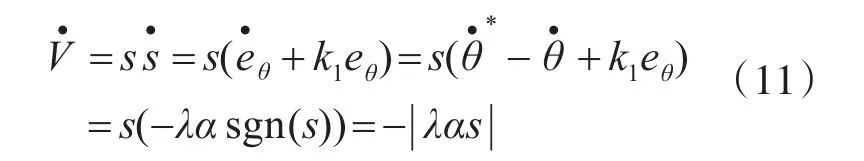
4 仿真实验和分析

根据PMSM数学模型建立Matlab/simulink仿真模型，设计传统PID算法与一阶积分滑模控制算法进行仿真验证[7～11]，仿真模型如图2所示，仿真结果分别如图3、图4所示。

图3为PID控制算法与一阶滑模控制算法的阶跃响应曲线，表1为两种控制算法的阶跃响应性能参数分析结果，可以看出，针对固定的被控对象及较精确的模型，两种控制方法均可以通过整定控制器参数实现理想的控制性能。

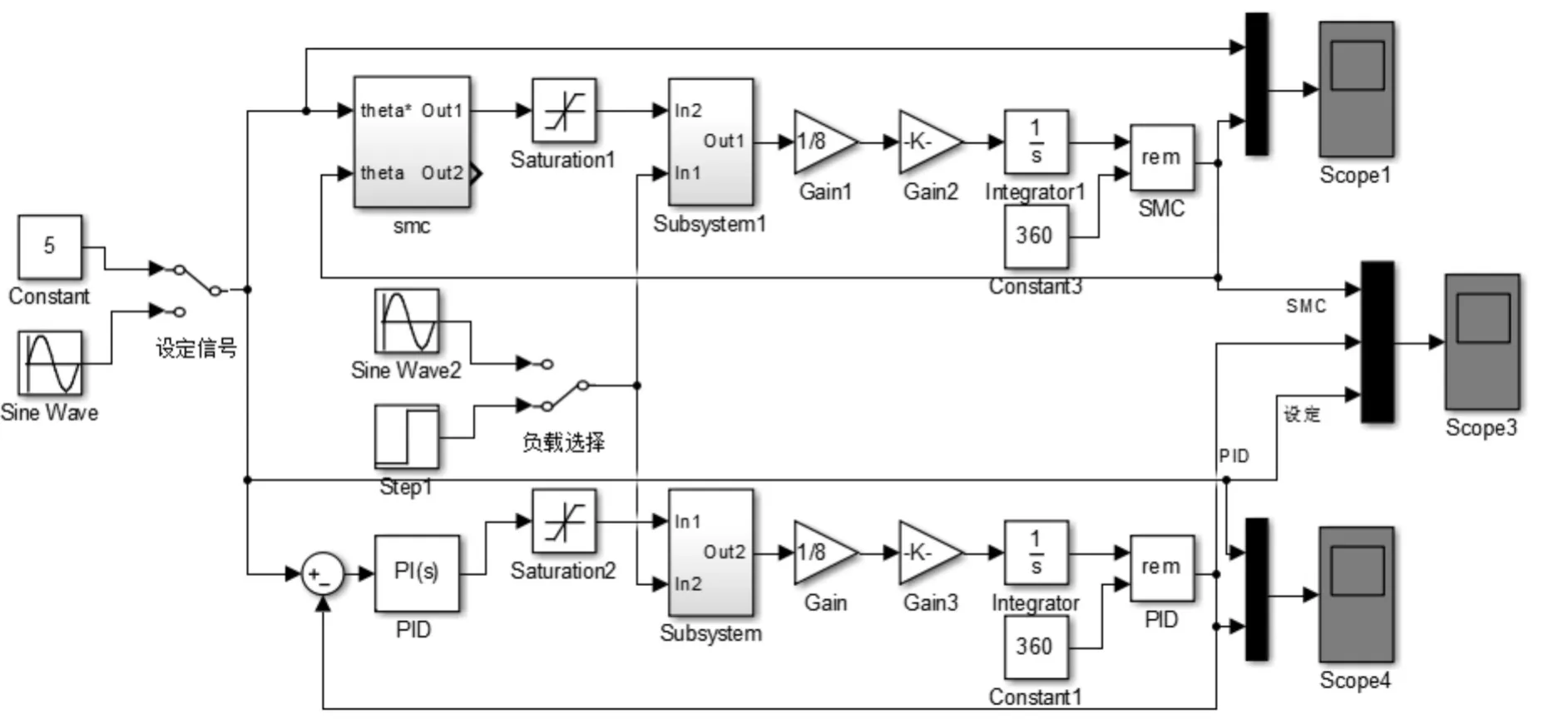
图2 Matlab仿真模型

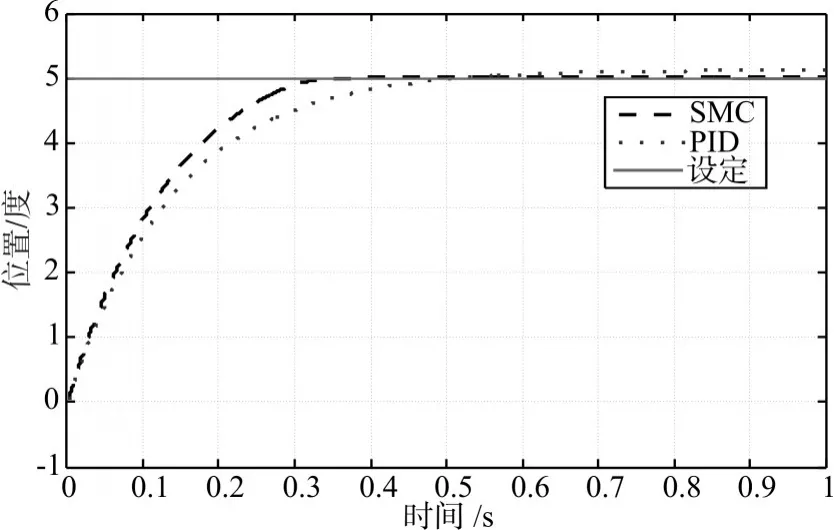
图3 阶跃响应曲线

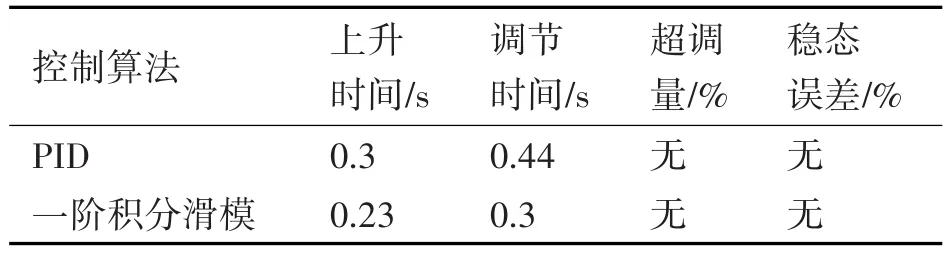
表1 阶跃响应性能参数

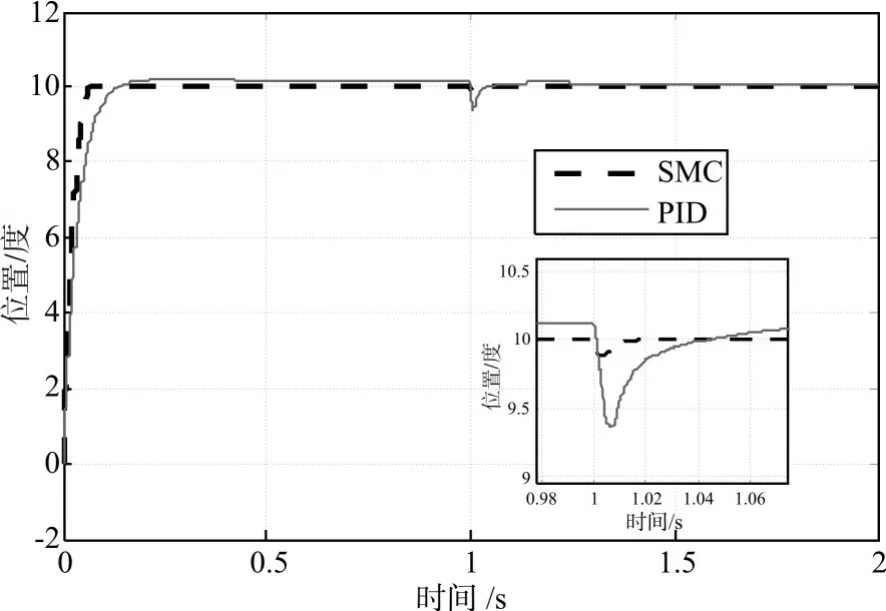
图4 负载干扰情况下方位控制曲线

图4为PID控制算法与一阶积分滑模控制算法抑制负载扰动的动态曲线，可以看出在负载发生变化的瞬间，一阶积分滑模控制下位置控制受负载变化较小，能够有效抑制风力矩及不平衡力矩突变的影响；PID控制不能有效抑制负载干扰，位置控制受负载干扰影响较大，位置角度波动较大。

5 结语

建模仿真结果显示，相对于传统PID控制算法，一阶积分滑模控制算法具有较快的动态响应和较强的干扰抑制能力，能够较为有效地抑制负载突变带来的影响，为工程应用奠定了基础。