基于十字阵列被动超声的发动机噪声定位研究∗

2020-10-30

舰船电子工程 2020年9期

（广州恒源动力机械有限公司广州 510000）

1 引言

声测试技术不断与信息处理技术、电子技术、自动化技术相融合，促进了声测系统的不断完善，这也因此使得声测技术成为了现阶段被广泛应用于各类测试领域的一项关键侦察技术。同时，声测技术也逐渐由原先的军事应用领域扩展至民用领域，取得了一系列重要的研究成果，包括免提电话、阵列助听器等。同时，这些技术的不断应用也促进了声传感器的快速发展，并表现出智能化、集成化、薄膜化的新发展趋势，这对声探测与其它各个领域的技术应用发挥了关键作用。

被动声目标定位指的是传声器以被动方式进行工作，根据目标噪声信号来完成目标定位的过程。为了实现被动声目标的定位与跟踪，需要设置具有优异探测功能以及简单结构的传声器阵列；根据探测维度的不同可以将传声器阵列布设结构分成平面、线型与立体阵列共三类。其中，线型阵列的探测范围是阵列构成的直线作为边界的半个平面，只能对目标二维参量进行探测；同时当目标的位置处在线型阵列端射角度下时，将无法通过线型阵列来完成测距功能；平面阵列可以实现比线型阵列更强的定位功能，除了可以对整个平面实施目标定位以外，还能够对阵列平面边界的半个空间范围实施定位，获得目标三维参量；定位功能最强的是立体阵列，能够完成整个空间的定位，不过需要采用复杂的定位算法进行分析。

2 被动声定位算法

根据测试依据的不同可以把被动声目标定位分成如下两类：第一类是根据时延估计（各传声器接收到信号的时间差）来计算目标参数的测试方法，第二类是根据瞬时频率来计算参数的测试方法。其中，第一种测试方法可以达到更高的测试精度，同时具备良好的抗干扰能力，已经成为现阶段被动声测系统的一类普遍测试方法。

时延指的是计时起点相同的二个传声器在接收信号过程中产生的时刻差，是二个信号产生时间延迟。根据以上分析可知，包含n个传声器的阵列将会产生n-1个时间延迟；为了测试平面目标的位置应至少配备3个传声器来生成2个时延；对空间目标进行定位时应至少配备4个传声器来产生3个时延；考虑到在实际应用中会受到区域条件以及阵列设计方法的限制，无法在传声器阵列中加入很多的传声器元件数量。假定阵列含有的传声器都是属于具有相同性能的全方向传声器。

根据声信号传输至传声器的时间差，即时延来完成目标定位的计算公式如下：

上式的（x，y）表示目标信号所在的坐标参数，(xi，yi)，(xj，yj)是阵列的传声器i与j的各自坐标，c是声波传播速度，τij代表声波传输至传声器i与j的时间差。

受上述方程非线性的影响，难以对其进行直接求解得到所需结果，需要采用迭代法进行求解，通过对近似解进行不断精确化处理的过程来获得最终的结果。

未知参数的个数决定了所需方程的个数，在使用牛顿迭代法求解目标位置坐标时至少需要2个非线性方程。计算过程如下：

雅克比矩阵为

当雅克比矩阵为非奇异矩阵时，有

此时牛顿迭代格式可用表达式表示为

需要有较好的初值x(0)，且[f'(x，y)]-1存在，即det(f')≠0，具体表示为

现在以二维空间为例，简要说明其计算过程：首先选取初值（x0，y0）进行计算、根据运算式求得（△x，△y）；当（△x，△y）中绝对值的最大值大于所设定的偏差值时，将进行下一步的迭代运算；重新设置（x0，y0），即令x0=x0+△x和y0=y0+△y，然后再次计算；重复上述运算直到（△x，△y）中绝对值的最大值小于所设定的偏差值为止。

3 任意阵列定位算法

在早期的分析研究中，被动声目标定位方法是建立在求解一系列非线性方程组的基础上的，它主要通过迭代算法的求解来达到目标定位的目的；但迭代算法要求有一个接近真实解的初值，而在实际中选取这个初值是有一定困难的，而且迭代算法的收敛也是有一定条件的，也就是说其收敛性得不到保证。在下面的分析中，将提出另外一种算法，这种算法将排除迭代算法所产生的问题，而且不受阵列形式的限制。

假设被动声定位系统（传声器阵列）包含一个标准传声器，n个子传声器。令（xj，yj，zj），j=0，1，2，…，n，表示每个传声器的位置坐标，0位置处的传声器表示标准传声器，其余位置处的传声器为子传声器。（x，y，z）表示目标的未知位置；rj表示目标声源到第j号传声器的距离；△rj表示目标声源到标准传声器和第j号传声器之间的路程差。

根据距离公式，则可列方程组如下：

其中 i=1，2，…，n。

将式（7）中的前两项相减，并通过化简可得：

其中ki可表示为

式（8）可表示为一系列的非线性方程，为求解这一系列方程，它们可用r0表示为

其中A、X、F分别表示为

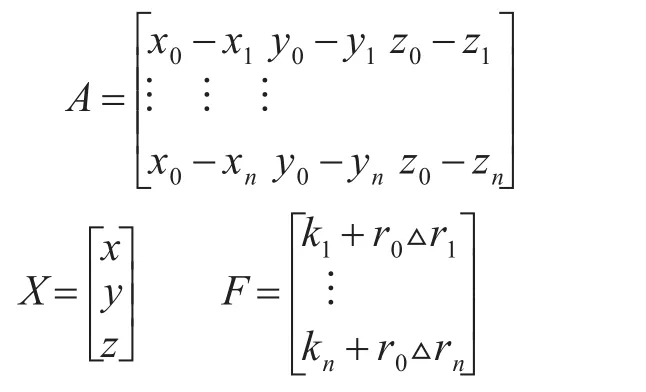
采用广义逆方法求解方程（10）可得

其中可将表示为

从方程（11）可知目标源的位置坐标可用r0来表示，即

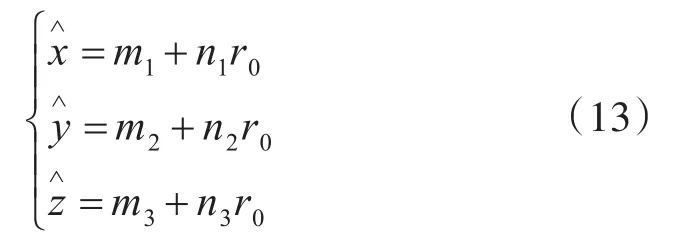
其中m，n可表示为

将方程（14）代入方程（7）中第一项，化简可得一关于r0的一个一元二次方程，即

其中

对方程（16）进行求解：由一元二次方程的性质可知，当△=b2-4ac大于等于零时，方程有解；而且当△等于零时，方程式有两个相同的根，即r01=r02：此时根据实际情况距离应为正的条件下，来判断是否为所需求的解。若△大于零时，方程具有两个不相同的根，如果，可知两根异号，其中一根为正，另一根为负，正根即为我们所要求解的目标位置距离；如果，，则两根同号，且当r01+r02＞0时，可判断出两根均为正值，此时需要通过进一步的判断来决定哪个根为真正所需的：判断的原则就是将两个根分别进行反向运算，求取各自的时延值，将反向运算所求解的时延值与测量所得的相对应的时延值进行比较，当某一根的时延比较差值小于设定的偏差值时，此根即被认为是所求解的值r0；将所求得的r0值代入式（16），即可求得目标声源的位置。上述分析是建立在假设有3个子传声器的基础上进行的。

4 采集噪声频谱分析

4.1 车辆噪声信号产生机理

汽车行驶过程中发动机的工作噪声包含空气动力噪声与机械噪声两种。其中，机械噪声是由传动系统中的链传动结构、曲柄活塞、轴承、液压系统结构等各类机械运动部件受到交变力作用而产生的，这类引起噪声的载荷作用主要来自燃料在发动机内的燃烧过程产生的燃烧激振力以及机械激振力。同时，发动机的固定组成部件受到激振力作用后机器在行驶期间受道路颠簸振动而导致机构噪声也属于一类重要的机械性噪声。车体机构噪声属于机械噪声的最主要来源。机械噪声在空气中都是以高频声传播，因此会被快速吸收而消耗，此类噪声只能在近声场区域内发挥作用，无法被用于远距离的测试与识别过程。

空气动力性噪声的组成包括发动机排气噪声、进气噪声、冷却风扇噪声等。其中，进气噪声属于发动机对空气进行周期性吸入使气缸产生压力脉动后，空气在进气道内保持自振频率振动状态，由此形成噪声。按照噪声强度由小到达排序为冷却风扇噪声＜进气噪声＜排气噪声。可以发现，排气噪声属于一类具有较大影响的气动噪声，这也是一类最主要的发动机噪声源。内燃机都是以周期性的方式向外排出气体，会对排气口附近的空气压强与密度也产生明显扰动，进入势核尾部区域剪切层中时，气流发生了明显湍化，使其内部应力发生明显改变，因此气流中的介质密度、运动形态及压力也呈现脉动状态，将会产生很强的辐射噪声。