锂离子电池容量退化融合估计算法∗

（海军工程大学兵器工程学院 武汉 430033）

1 引言

锂离子电池具有能量密度高，质量轻，自放电率低的优点，但是还存在着很多安全性问题，比如使用过程中固体电解质界面膜的形成，电池内部电解液分解以及电极材料分解，剥落或腐蚀等，会造成电池容量的退化，使电池可靠性降低[1]。当容量退化到不能满足设备继续工作或规定值（失效阈值）之前所经历的充放电循环次数被称为电池循环寿命[2]。

目前在电池容量估计方法主要分为基于经验，基于电池机理，数据驱动的方法。基于经验的方法只有在电池的经验知识比较充分的情况下才能获得有效的预测。基于电池机理的方法的问题在于电池真实模型内部反应机理复杂。数据驱动的方法能从数据中挖掘电池性能老化的规律，有效避免复杂电化学模型的建立[3]。数据驱动算法包括人工智能和统计数据驱动两个方向，人工智能方向有神经网络[4～5]，支持向量机[6]，模糊模型等方法。统计数据驱动包括回归模型[7～8]，马尔科夫模型，粒子滤波[9～10]，维纳滤波，卡尔曼滤波[11]等方法。锂离子电池是典型的非线性动态电化学模型，目前其内部参数的测量仍存在困难，数据驱动的方法不需要考虑电池内部机理，通过大量外部观测数据去寻找退化的表征。

本文根据已有电池容量退化数据，利用欧式距离刻画数据间的相似度，通过神经网络建立容量退化模型，最后用粒子滤波追踪模型内部参数，提出了一种锂离子电池容量退化估计的融合算法。本文首先介绍所采用的神经网络模型，然后给出融合算法的步骤。最后，通过实验与经验双指数模型粒子滤波算法进行对比，验证算法的有效性。

2 Neural Networks神经网络

神经网络通常由输入层，隐含层，输出层组成。图1为本文的神经网络拓扑结构。

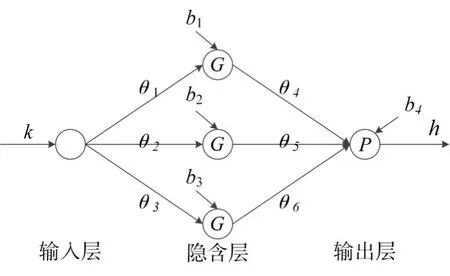
图1 神经网络拓扑结构

输入层k是网络输入。隐含层每个神经元激活函数为G（x），通常被称为tansig函数。输出层激活函数为Q（x），通常被称为purelin函数，最终输出为对应的电池容量。函数具体表达式如下：

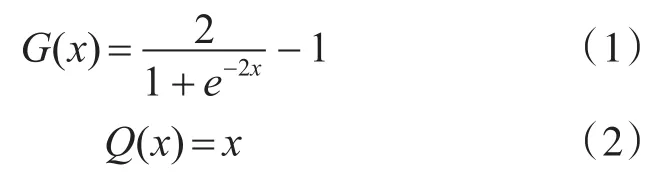
由上面的网络结构，可以得到观测模型方程。

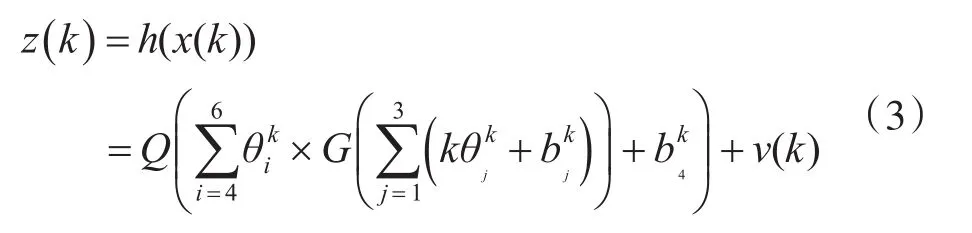
其中k为电池充放电的次数，z(k)为电池在k时刻的电池容量，v(k)为观测噪声。模型一共有10个状态参量。

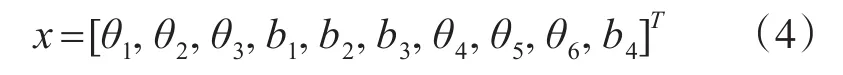
3 NNPF算法原理

3.1 Particle filter粒子滤波

粒子滤波算法是一种基于蒙特卡洛方法和递推贝叶斯估计的统计滤波方法。其基本思想是依据系统状态向量的先验条件分布在状态空间产生一组被称为粒子集的随机样本集合，然后根据测量值不断调整样本粒子集状态及权值，使其近似系统状态向量的后验条件概率分布。粒子滤波算法通过序贯重要性采样赋予每个粒子权值，并通过重采样[13]对权值过小的粒子进行替换，使得粒子的分布更加符合后验概率密度函数。

3.2 神经网络和粒子滤波融合算法NNPF

融合神经网络和粒子滤波算法首先要建立电池状态空间模型以及观测模型。神经网络能够通过神经元及其激活函数来近似拟合非线性系统。粒子滤波能够有效通过粒子集近似系统状态后验分布。

由式（3）和（4）可知，测量方程为

状态方程为

其中x(k)为k时刻的状态值，w(k)为状态噪声。

算法基本步骤如下：

1）初始化参数

通过BP神经网络拟合初始值X0，然后通过噪声生成初始粒子集。初始化状态噪声为

其中的k作用是调节噪声的变化范围，这样设置噪声能够让算法的搜索范围由大到小，提高粒子样本量。

2）相似性处理与归一化

因为隐含层激活函数最佳范围在[-1.7，1.7]之间，所以需要对输入值进行归一化。

假设待预测预测的数据点数为N，将其与其他几条退化曲线进行相似性度量，计算待测曲线与其他曲线的欧式距离Di，根据Di给每条曲线相应的权值，最后将各条曲线的失效点加权得到待测曲线得到归一化值。

其中x是待预测的数据点集，xi是第i条已知退化曲线的数据点集。

得到了待预测点集对于其他已知数据集的相似度量后，越相似的数据点集之间的相似度量程度会越小，通过，再对归一化处理，加权得到归一化预估值：

得到归一化最大值后：

在式（10）中，k是是数据的循环次数，k'是归一化后的循环次数。

3）粒子重要性权重

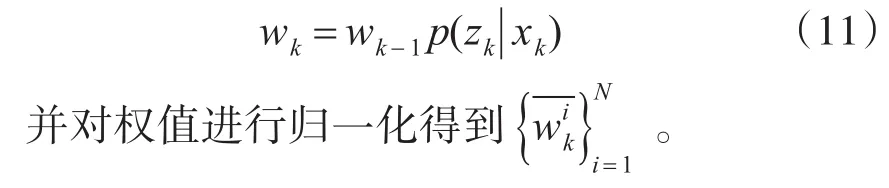
4）粒子重采样

计算粒子集的离散程度，对小于阈值的粒子集进行重采样，并重置权值。

5）算法迭代

令k=k+1，然后重复上面第2）步直到循环周期达到预测点，将最终的状态值代入观测方程，计算预测的电池容量衰减曲线。

4 实验结果分析

本文采用马里兰大学CALCE实验室环境下测试得到的电池容量退化原始数据对算法进行验证。A3，A5，A8，A12是四组不同的电池退化曲线（图2）如下。本文取4个循环时间节点，分别为k=30，50，100，150，并与标准PF算法进行结果对比。

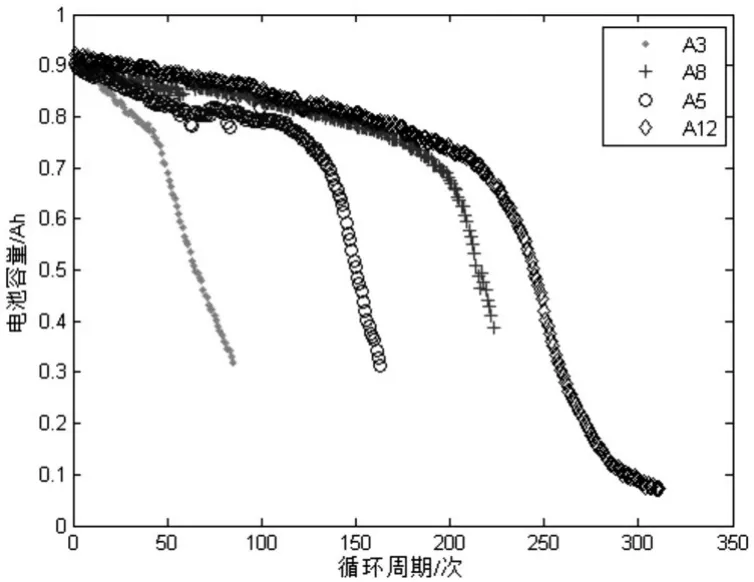
图2 电池容量退化数据

以A5数据为预测对象，根据算法步骤，失效阈值为锂离子电池容量的70%，在k=206处。对参数设置如下：失效阈值为u=0.63Ah，粒子数N=500，状态协方差设置如算法部分，状态噪声本文取wa=0.01，wb=0.0001，观测噪声值为V（k）=0.01。

利用A8电池的退化数据进行初始化，将A5与其他三组数据集进行相似性度量，得到归一化值。然后通过绝对误差和相对误差对计算结果进行分析：

绝对误差公式：

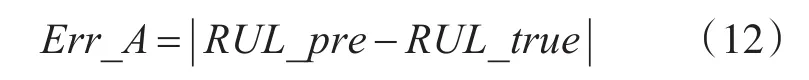
相对误差公式：

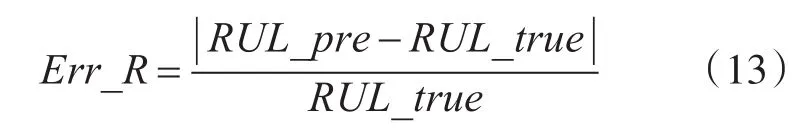
其中RUL_pre是电池容量预测值，RUL_true是电池容量真实值。

因为算法获得的结果有一定的随机性，所以本文还用大量重复实验获得预测值的均值和方差，以消除随机性带来的误差，重复实验组数为100次。

仿真利用最常见的经验双指数模型[15]结合PF算法进行对比。结果如表1、2所示。

表1 标准PF算法分析

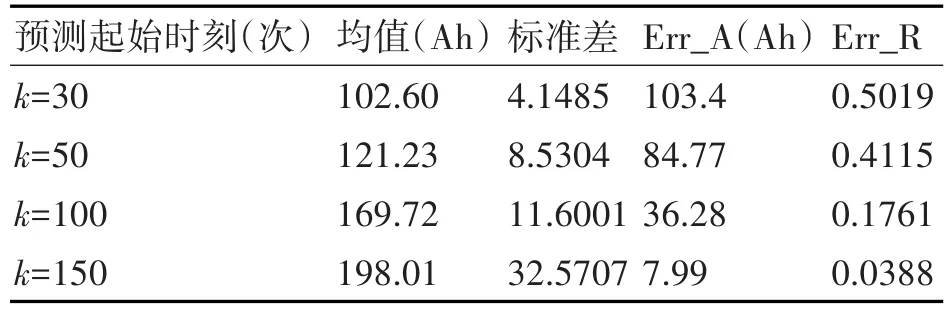
表2 NNPF算法分析

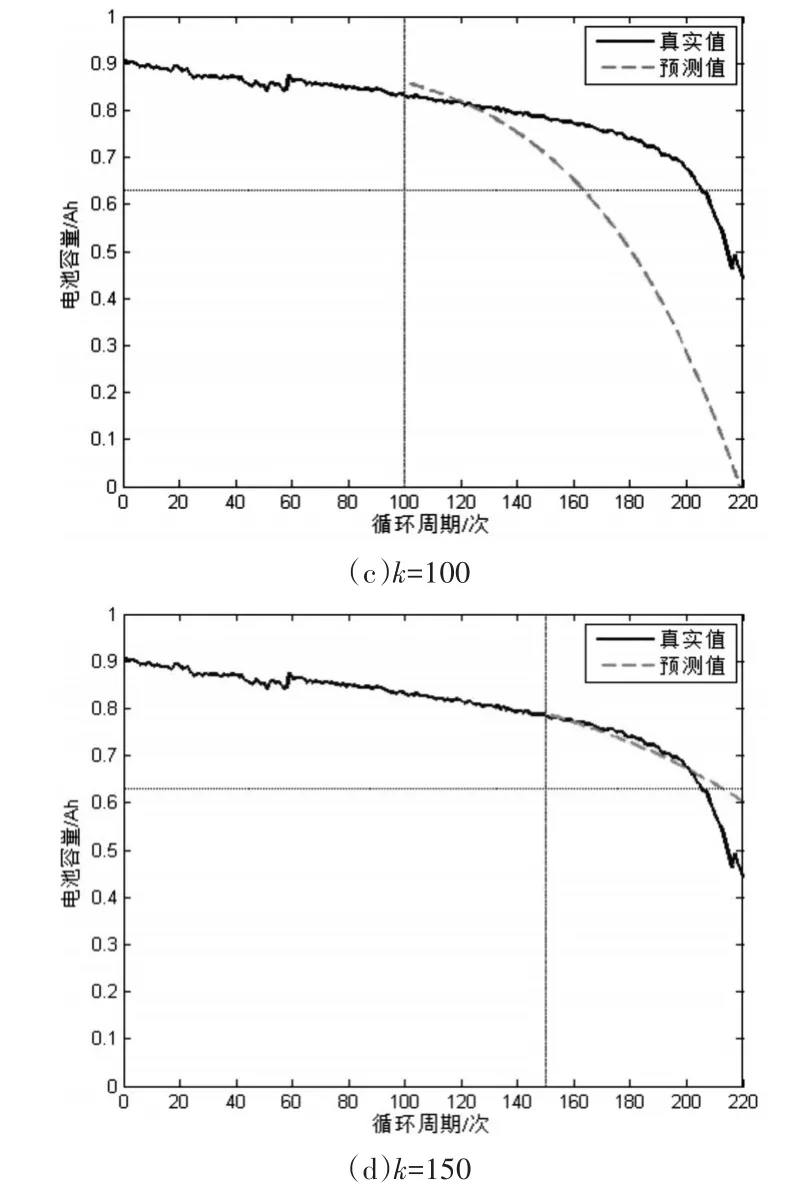
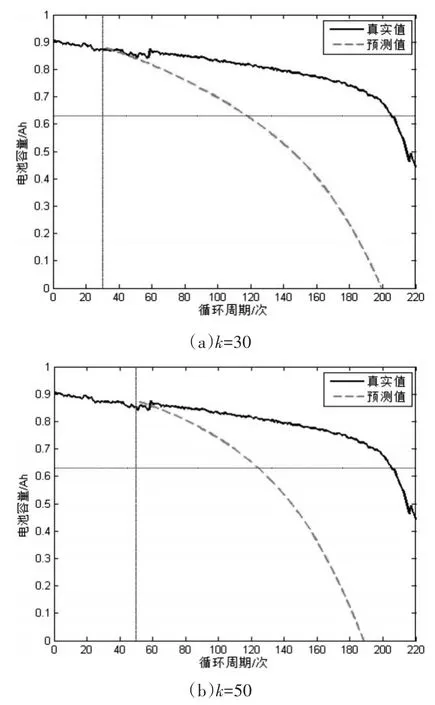
图3 标准PF算法在k=30，50，100，150时结果

由图3看出，基于双指数模型的PF算法相比融合算法短期预测效果不好。

由表1可以看出NNPF算法的短期预测和长期预测效果，都要好于PF算法。从准确性上来说，在k=30时，NNPF算法的误差比PF算法少30%左右，在k=150时，NNPF算法的误差比PF算法也要少10%。算法稳定性上，NNPF算法的方差比PF算法少0.1到0.2左右。分析原因，数据集相似性度量带来的归一化给模型参数的变化设定了一个初步的范围，所以粒子滤波在追踪过程不会产生太大的偏差，算法呈现出由粗到细的搜索策略。

5 结语

本文提出的融合算法，利用神经网络对电池容量衰退的非线性过程进行建模，在建模时加入了数据集间的相似度量，考虑了数据之间的联系，同时利用粒子滤波算法建立观测值与神经网络模型状态值的联系。在与标准PF算法的比较中，证明了算法的有效性。本文所做的工作还有不足，一是实验数据集数目较少，大量数据下的算法有效性没有得到验证。二是算法运算时间较长，应用到锂离子电池容量退化的实时监控还需改进。