套筒连接的预制拼装桥墩抗震性能研究

徐文靖，马 骉，黄 虹，苏 俭，李建中，王瑞龙

(1. 同济大学土木工程防灾国家重点实验室，上海 200092；2. 上海市政工程设计研究总院(集团)有限公司，上海 200092)

预制拼装技术由于具有施工时交通干扰少、现场施工工期短、噪声低、环境污染小等优点，在城市桥梁建设中得到广泛应用[1]。随着对下部结构的研究深入，预制拼装技术在桥梁下部结构中的运用得到越来越多的关注[2−3]。20 世纪60 年代Yee 等[4]提出在预制拼装结构中采用套筒灌浆的连接方式，解决了装配式构件中的纵筋连接问题，为预制拼装桥墩提供了一种切实可行的连接方法。

钢筋套筒灌浆连接技术主要应用于预制构件的钢筋连接、钢筋笼整体对接以及既有建筑的改造工程中[5−6]。国际上众多学者针对钢筋套筒灌浆技术开展了较多的研究工作，对钢筋套筒灌浆连接试件在拉伸荷载作用下的力学性能及破坏形态进行了深入分析[7−9]。近年来，随着预制拼装桥墩的兴起，钢筋套筒灌浆连接技术在预制拼装桥墩的构件或节段之间的连接应用得到密切关注。

目前，国内外学者针对灌浆套筒连接的预制拼装桥墩进行了大量的试验研究。魏红一、王志强等[10−11]通过对套筒预埋位置不同的预制桥墩进行拟静力试验，并与现浇桥墩对比，表明不同预埋位置的灌浆套筒预制试件在损伤形式和塑性铰形成上有所不同，但抗震性能总体相近，预制试件的损伤均小于整体现浇试件，且主要集中在接缝处；Haber 和Pantelides 等[12−13]学者分别进行了灌浆套筒的拟静力试验，均发现采用套筒灌浆连接的预制拼装桥墩，其位移承载能力与整体现浇桥墩相比减小了25 %～40 %，且预制桥墩的最终破坏模式主要有以下三种：接缝处钢筋断裂、搭接钢筋从套筒滑出和套筒自身破坏；Tazarv 等[14]根据灌浆套筒的性能特点，提出了灌浆套筒放置于塑性铰区域后桥墩塑性铰高度的修正公式，为灌浆套筒连接的预制拼装桥墩提供了理论分析依据。然而，目前对于灌浆套筒连接的预制拼装桥墩的最终破坏形式研究较少，现有文献中很少涉及灌浆套筒连接的预制桥墩在接缝处的受力机理，关于接缝处的力学行为对桥墩整体抗震性能影响的研究几乎处于空白。

本文首先通过理论分析，研究了采用灌浆套筒连接的预制拼装桥墩在墩底接缝处的受力机理以及套筒段刚性区域的力学行为对桥墩抗震性能的影响。在此基础上，采用拟静力方法研究了灌浆套筒连接的预制拼装桥墩在水平往复荷载作用下的受力性能。同时，采用数值模拟方法，分析比较了灌浆套筒桥墩与整体现浇桥墩的性能差异，探讨了不同套筒直径和长度对灌浆套筒桥墩接缝处的性能影响，为实际桥梁工程的运用提供参考依据。

1 灌浆套筒桥墩受力机理

1.1 灌浆套筒工作原理

对于预制拼装结构，构件或节段间的有效连接对结构整体性能影响重大，其中灌浆套筒连接是预制拼装桥墩常采用的连接方法。灌浆套筒连接(见图1)依靠灌浆料与钢筋和筒壁间的黏结来达到钢筋对接锚固作用，钢筋与灌浆料和灌浆料与套筒内壁之间的黏结作用由材料黏附力、表面摩擦力和结合面之间的机械咬合力构成。同时，套筒可有效约束灌浆料，增强结合面处的黏结锚固作用，确保灌浆套筒的传力能力[15−16]。当钢筋受到拉力作用时，拉力通过钢筋-灌浆料结合面与灌浆料-套筒结合面，从内部钢筋传递到外部套筒，完成力的传递。灌浆套筒的理想破坏模式为套筒外的钢筋被拉断，为避免套筒先于钢筋发生破坏，套筒一般采用球墨铸铁或优质碳素钢铸造而成，以确保套筒具有较高的强度与刚度。

图1 灌浆套筒连接方式Fig.1 Grouted splice sleeves

1.2 灌浆套筒桥墩受力分析

对于现浇桥墩，在地震荷载作用下，桥墩墩底为薄弱部位，在距墩底一定高度内桥墩发生塑性变形。欧昱辰等学者[17]提出桥墩的极限位移定义为，当桥墩达到以下三种极限状态之一时，墩顶所能达到的最大位移：1)核心混凝土达到极限压应变，即核心混凝土破坏；2)钢筋达到极限拉应变，即钢筋拉断；3)桥墩承载力下降至峰值承载力的80%。桥墩的极限位移 ∆u由两部分组成：桥墩自身弹性变形引起的屈服位移 ∆y和塑性变形引起的塑性位移 ∆p(见图2)。

图2 桥墩变形图Fig.2 Deflected shape of pier

对于受弯为主的单柱墩，其墩顶位移与桥墩的曲率分布之间存在如式(1)所示关系：

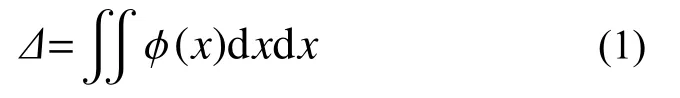
当墩底截面刚达到屈服状态时，墩身曲率可近似认为沿墩高线性分布(见图3(a))，通过曲率积分，可得此时墩顶的屈服位移为：

式中： ϕy为截面理论屈服曲率；L为墩底截面到墩顶的距离。

图3 桥墩曲率分布图Fig.3 Curvature diagram of deflected pier

当墩底截面曲率达到极限曲率时，实际墩身曲率沿墩高的分布曲线如图3(b)所示， ϕp为截面的塑性曲率。为了便于分析，各国规范[18−19]引入了“等效塑性铰长度”的概念，即假定桥墩屈服后弹性曲率仍沿墩身线性分布，而塑性曲率在等效塑性铰长度Lp范围内均匀分布[20−21]，墩顶的塑性位移为：

对于灌浆套筒连接的预制拼装桥墩，套筒通常预埋在墩柱底部，即传统桥墩的塑性铰区域内，以实现承台与墩柱的连接，如图4(a)所示。图4(a)中Lsp为套筒长度，Hsp为套筒底端距承台的垂直距离(即接缝高度)，我国Hsp一般接近于0，即接缝位于墩底。当桥墩以弯曲受力为主时，由于套筒自身刚度和面积较大，套筒区域一般不会屈服，使得桥墩的非弹性变形发生在套筒区域以外地方，桥墩墩身的曲率分布与传统整体现浇桥墩的曲率分布存在差异(见图4(b))。图4(b)中虚线为传统整体现浇桥墩曲率简化分布情况，实线为墩柱预埋套筒桥墩的曲率分布情况。由(见图4(b))可以看出，在水平力作用下，由于灌浆套筒面积远大于钢筋面积，套筒区域内曲率较小，而与套筒相连的交界处，曲率增大，尤其套筒底部与承台顶部相连的接缝处曲率增加更多，已有试验研究表明[12−14]，套筒底部与承台顶部的接缝距离越小，曲率增加越明显，钢筋应变集中现象越突出。

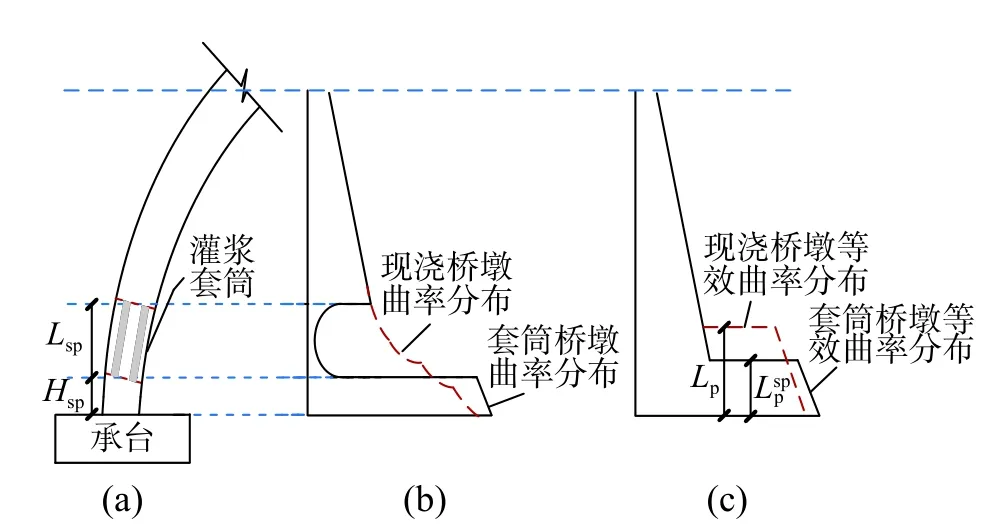
图4 灌浆套筒桥墩曲率分布Fig.4 Curvature diagram for column with grouted sleeves

同时，墩顶的极限位移与桥墩的曲率分布息息相关，当在墩底埋置套筒后，墩身曲率重新分布，套筒段刚性区域一般在弹性范围内，当连接套筒长度较长时，桥墩的塑性变形主要集中在墩底接缝处。相比较于整体现浇桥墩，如假设塑性曲率在等效塑性铰长度Lp范围均匀分布(如图4(c))，则灌浆套筒连接的预制拼装桥墩等效塑性铰长度Lspp比整体现浇桥墩的等效塑性铰长度Lp要小。美国推荐的《AASHTO 预制拼装结构设计和施工规范》[22]通过修正(减小)灌浆套筒连接桥墩的等效塑性铰区域长度，来计算极限位移。建议的灌浆套筒连接桥墩塑性铰等效长度Lspp计算公式为：

式中：Lp为整体现浇桥墩的塑性铰长度，计算公式可参考AASHTO 规范[22]或《城市桥梁抗震设计规范》[18]；Lsp为连接套筒长度；Hsp为套筒底端与承台之间的距离，即为接缝处高度； β为连接段刚性长度因子，根据推荐的《AASHTO 预制拼装结构设计和施工规范》[22]， β取值0.75 较为合理。

由式(5)计算出的灌浆套筒连接预制拼装桥墩的接缝高度Hsp和套筒长度Lsp对桥墩等效塑性铰长度Lspp的影响如图5 所示。从图中可以看出，对于给定的套筒长度，灌浆套筒桥墩的等效塑性铰长度随着接缝高度的增大而增大；对于给定的套筒底端与承台间的距离，桥墩的等效塑性铰长度随套筒长度的增大而减小。

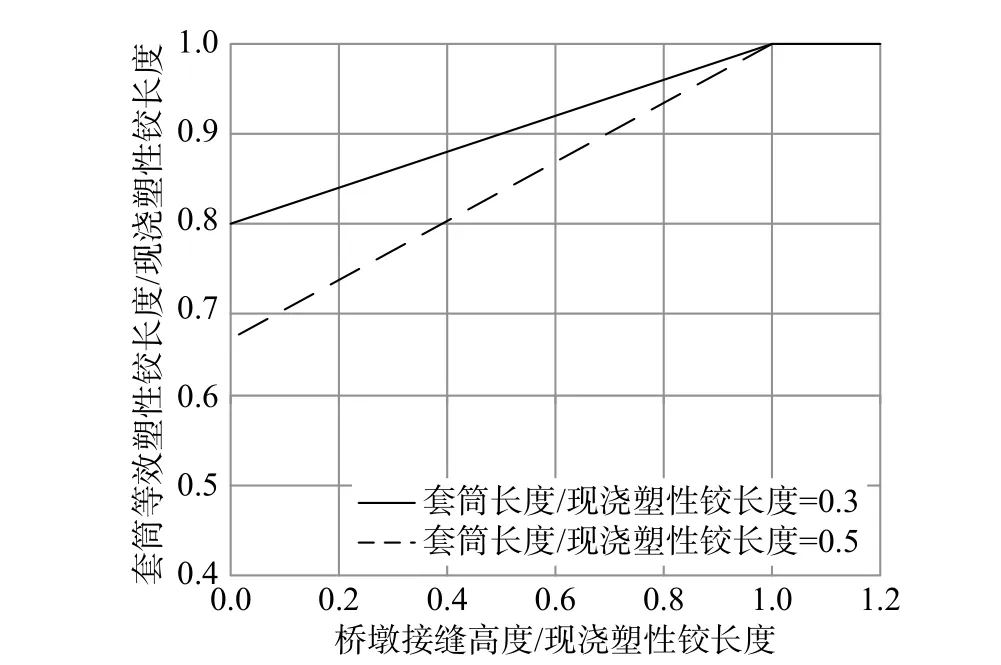
图5 灌浆套筒等效塑性铰长度变化规律Fig.5 Variation of plastic hinge length of grouting sleeve

确定了等效塑性铰长度后，灌浆套筒连接的预制拼装桥墩墩顶极限位移可以按下式计算：

式中： ∆′u为灌浆套筒连接的预制拼装桥墩墩顶极限位移； ∆′p为灌浆套筒连接桥墩墩顶的塑性位移。

2 试验验证

2.1 试验设计和制作

为验证上述对灌浆套筒桥墩受力分析的正确性，本文结合实际工程背景，设计了墩身埋置灌浆套筒的桥墩试件(见图6)。试件墩身设计尺寸为600 mm×600 mm×3760 mm，加载端尺寸为900 mm×900 mm×3000 mm，底座尺寸为2400 mm×2400 mm×600 mm，试件加载中心到立柱底的距离为4210 mm，试件的剪跨比为7。墩身与底座混凝土的强度等级均为C40，墩身配筋如图7 所示，主筋采用直径40 mm 的HRB400 热轧带肋钢筋，配筋率1.4%。墩身和承台主筋锚固在灌浆套筒中，灌浆料采用强度100 MPa 的高性能灌浆材料，套筒长度为800 mm，套筒构造如图8 所示。

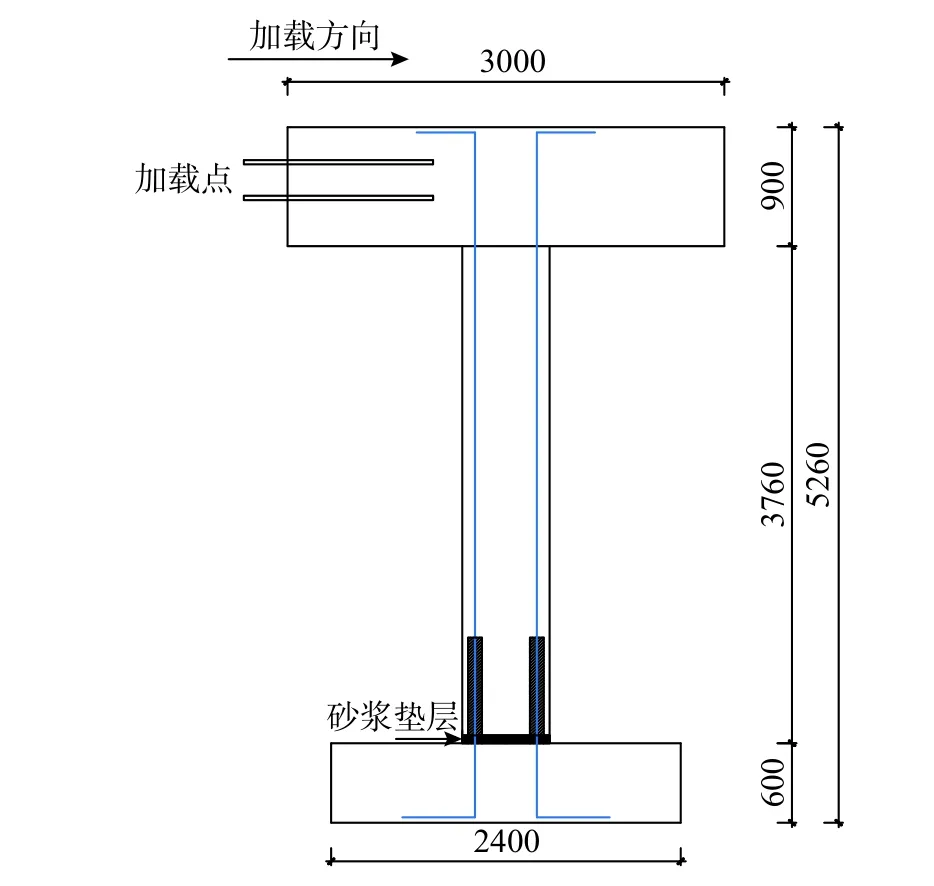
图6 试件构造示意图 /mm Fig.6 Geometry of pier specimens

图7 立柱截面配筋设计 /mm Fig.7 Reinforcement arrangement of pier specimens

2.2 试验加载装置及加载制度

图8 灌浆套筒构造示意图 /mm Fig.8 Details of grouted splice sleeve

图9 试验加载装置Fig.9 Experimental loading device

灌浆套筒连接的预制拼装桥墩拟静力试验加载装置如图9 所示，竖向承受恒定轴向压力，轴压比为15%，水平向进行循环荷载加载直至破坏。试件的竖向荷载通过两个竖向作动器对称施加在横梁上，水平荷载通过一个水平作动器施加。水平加载时，采用先力控制、后位移控制的加载方法。力控制阶段，水平力由50 kN 每隔50 kN增加直至墩底主筋接近屈服；转为位移控制，墩顶位移由20 mm 先每隔10 mm 增至60 mm，超过60 mm 后，设定每个荷载等级位移加载幅度为30 mm，直至桥墩达到破坏状态[23]。每次加载阶段均采用3 次循环加载，每次循坏加载到最大力(位移)时持载，进行破坏现象的观察和记录工作。

2.3 试验结果和分析

2.3.1 试件损伤现象描述

为便于描述，将立柱的四个面进行了标记，水平助动器的加载面为E 面，其余三个面按照立柱俯视图中逆时针方向，依次标记为N、W、S 面(见图10)。

图10 试件标记示意图Fig.10 Label of pier specimen

力控制加载初期，当水平力加载到100 kN时，墩身首次出现受拉裂缝，裂缝的位置位于套筒段中部(距离墩底400 mm)和套筒段上方(距离墩底1000 mm)，此时试件接缝未张开，坐浆层保持完好，表明低荷载水平下接缝处为非薄弱环节。

随着荷载增大，墩身出现多条弯曲裂缝和斜裂缝，各条弯曲裂缝间距约200 mm，分布在距离墩底1200 mm 的高度范围内，如图11 所示。当完成±150 kN 力控制加载时，墩底纵筋接近屈服，此时转换为位移控制加载，当侧向加载位移为30 mm时，墩底纵筋应变约为2000 µε，达到屈服。

图11 试验裂缝分布Fig.11 Crack distribution of specimen

当加载位移为60 mm 时，坐浆层开始有裂缝产生。当加载位移为120 mm 时，坐浆层混凝土破坏明显，墩角混凝土出现轻微剥落，此时可通过坐浆层破坏处开口微见套筒底部。在进行±210 mm级位移加载工况下，当正向位移达到150 mm 时，E 面对应的墩底接缝处钢筋发生断裂，桥墩承载力降低，无法达到目标位移210 mm。同样，在进行反向210 mm 位移加载时，W 面对应的墩底接缝处钢筋在位移加载到150 mm 左右时发生断裂，桥墩承载力迅速降低，两侧承载力均下降到峰值承载力的80%，加载结束。

试验结束后，清理墩底接缝处破坏的砂浆和保护层混凝土后，试件的破坏状态如图12 所示。从图中可以看出，试件的最终破坏形态与前述理论分析结果一致，墩身底部套筒区域因套筒面积较大，混凝土损伤较小，箍筋没有屈曲、外鼓，核心混凝土保持完好。试件的破坏区域集中在墩底接缝处，接缝处混凝土压溃，搭接钢筋断裂，导致桥墩承载能力迅速降低。

图12 试件最终破坏形态Fig.12 Characteristics of pier models

2.3.2 试验结果分析

结构的力-位移滞回曲线反应了结构的基本抗震性能，主要包括延性变形能力、滞回耗能能力以及残余位移等，根据滞回环的形态可以判断试件的破坏机制。图13 给出了本次试验试件的实测水平力-墩顶位移滞回曲线。从图中可以看出，试件在加载初期，基本处于弹性阶段，滞回环较为集中；随着混凝土裂缝出现、钢筋屈服，滞回环逐渐拉开；到加载后期，滞回环逐渐呈扁平的四边形，残余位移增大。在进行210 mm 级位移加载时，正反向加载位移到150 mm 左右时，滞回曲线均出现一个急剧的下降段(如图13 中虚线曲线所示)，此时E 面和W 面对应的墩底接缝处钢筋发生断裂，桥墩承载力迅速降低。

骨架曲线是将滞回曲线每次循环的峰值点连接起来，和单调加载时的力-位移曲线相似，只是极限荷载略低，能够比较明显的反应构件的初始刚度、最大加载力、屈后刚度、延性等抗震指标[24]。图14 为本次试验试件的骨架曲线图，可以看出试件的屈服点和强度下降点较为明显，当水平加载±90 mm 位移时，试件承载力达到最大值219 kN；进行最后一级位移加载，当位移达到150 mm 时，钢筋断裂，承载力降低，此时水平加载力为160 kN，约为最大加载力的73%，结构破坏。

图13 试件水平力-位移滞回曲线Fig.13 Hysteretic curves of load-displacement

图14 试件骨架曲线Fig.14 Skeleton curve of specimen

为了进一步探讨试件在各加载等级下的变形分布情况，图15 给出了试件各加载等级的实测曲率分布曲线。从图中可以看出，墩底接缝处曲率较大，随着墩高增加，曲率骤然减小，当墩高约为800 mm(即套筒顶部位置)时，墩身曲率有轻微增加。这表明立柱预埋套筒后，套筒区域处于弹性范围内，该区域曲率较小，使非弹性变形主要发生于套筒区域以外，尤其使得立柱与承台接缝处的曲率增大明显，变形更为剧烈。

图15 试件塑性铰区曲率分布Fig.15 Distribution of curvature in plastic hinge area

3 数值分析

为进一步分析探讨灌浆套筒连接对桥墩受力性能的影响，本文依据前述试验模型，采用OpenSees[25]建立有限元纤维模型，进行数值分析。

3.1 模型建立

为准确分析桥墩的力学行为，本研究中采用弹塑性纤维梁单元[26]来模拟钢筋混凝土桥墩。在纤维截面中，约束混凝土和保护层混凝土采用Kent-Scott-Park 混凝土本构模型[27]，其应力-应变如图16(a)所示；钢筋采用Giuffre-Menegotto-Pinto钢筋模型模拟[28]，应力-应变曲线如图16(b)所示。通过前述分析可知，墩身预埋套筒处因套筒自身刚度和面积较大，形成了一个相对刚性区域，等同于该区域设置了一根很粗的钢筋，在建立模型时，依据文献[22]对灌浆套筒的研究分析，可采用面积等效原则，将套筒等效为同等性能钢筋，同时相比较于套筒和主筋，套筒与主筋间的灌浆料强度相对较低，因此在模拟套筒连接段时，忽略套筒内灌浆料的影响，仅对套筒和套筒内的主筋进行等效处理。依据试验模型参数建立对应的纤维模型(见图17)，在纤维模型中，主筋直径为40 mm，套筒连接段等效为直径64 mm的钢筋。

图16 材料本构模型Fig.16 Material constitutive relationship models

3.2 与试验结果对比

图17 纤维模型Fig.17 Diagram of fiber models

图18 数值计算与试验结果对比Fig.18 Comparison between numerical calculation and test results

对建立的纤维模型进行往复推拉分析和推倒分析，分别将数值模拟分析得到的滞回曲线、骨架曲线和曲率分布曲线与试验结果对比，如图18所示。在有限元模型中，当钢筋发生断裂后数值分析难以收敛，因此往复推拉分析结果中只给出了钢筋发生断裂前的计算曲线。从图中可以看出，有限元计算结果与试验结果基本吻合，说明纤维模型中将套筒等效为同等性能钢筋的分析方法可以很好的模拟试验结果。从曲率对比曲线可以看出，有限元计算结果与试验结果均表明立柱预埋套筒后，在套筒段形成的相对刚性区域里，套筒区域在弹性范围，曲率较小，而墩底接缝处钢筋变形大，曲率数值较高，致使墩底接缝处为薄弱部位，易产生钢筋应变集中现象从而导致钢筋断裂。表1 给出了数值模拟与试验分析的屈服位移、屈服力、极限位移、极限承载力和接缝处曲率的结果对比情况，从表中可以看出，有限元模型数值计算结果与试验结果误差在20%以内，验证了有限元模型的正确性，为进一步的数值分析讨论提供了计算依据。

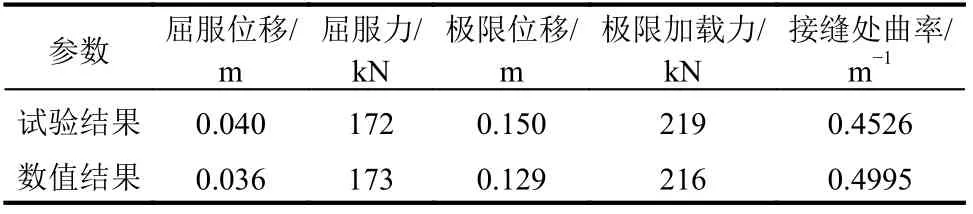
表1 关键数据对比Table 1 Comparison of key data

3.3 参数分析

通过分析和试验对比，验证了有限元计算模型的有效性，为了分析灌浆套筒桥墩与整体现浇桥墩的性能差异，以及进一步研究灌浆套筒连接预制拼装桥墩在地震作用下的受力性能，对套筒直经和套筒长度的效应进行参数分析。根据灌浆套筒的规格尺寸及相关技术要求，套筒直径的选取与钢筋直径一一对应，分析灌浆套筒直径对桥墩性能的影响即为探讨不同主筋直径的效应。

在参数分析时，套筒直径分别取66 mm、77 mm和95 mm，相应的主筋直径分别为20 mm、32 mm和40 mm，如表2 所示；针对套筒直径66 mm(即主筋直径20 mm)，套筒长度分别取360 mm、460 mm和560 mm 进行套筒长度的参数分析。

表2 模型参数 /mmTable 2 Characteristics of pier model

针对以上工况，采用3.1 节的模型建立方法，分别建立了整体现浇和套筒连接预制拼装桥墩共计8 个模型。

3.4 分析结果对比

对所有计算模型进行推倒分析，整理计算结果，对比如下。

3.4.1 极限位移对比

依据前述建立的有限元模型，计算分析各模型的极限位移，主筋40 mm(套筒直径95 mm)、主筋32 mm(套筒直径77 mm)和主筋20 mm(套筒直径66 mm)三个工况的最终破坏模式相同，对于整体现浇桥墩，加载过程中，墩底核心混凝土首先达到极限压应变，即整体现浇桥墩的破坏形式为墩底混凝土破坏；而对于套筒连接的桥墩，在加载过程中，钢筋首先达到极限拉应变，即套筒连接桥墩的破坏形式为钢筋拉断，桥墩不同破坏模式对应的极限位移有限元计算结果如表3 所示。同时，依据第一节所述的灌浆套筒连接的预制拼装桥墩等效塑性铰长度简化公式(5)和极限位移计算公式(6)，分别计算主筋40 mm、主筋32 mm 和主筋20 mm 灌浆套筒连接桥墩的等效塑性铰长度、极限位移和对应的整体现浇桥墩的塑性铰长度和极限位移，计算结果如表4 所示。

表3 不同套筒直径有限元极限位移计算结果 /mTable 3 Results of displacement capacity with different sleeve diameters calculated by finite element analysis

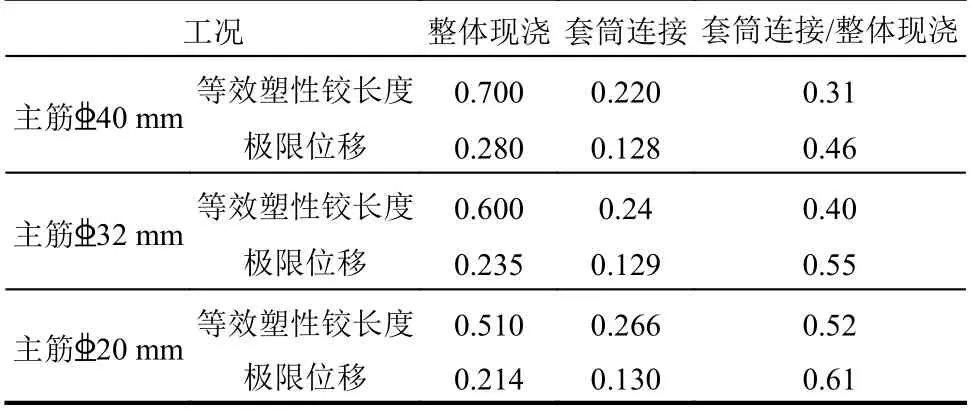
表4 简化公式极限位移计算结果 /mTable 4 Results of displacement capacity calculated by simplified formula

对比分析表3 和表4 可以看出，采用有限元建模分析得到的计算结果和简化公式计算得到的结果误差在10%以内。结合表3 和表4 数据可知，采用套筒连接后，主筋40 mm、主筋32 mm和主筋20 mm 三个工况套筒连接桥墩的等效塑性铰长度均比对应的整体现浇桥墩塑性铰长度小，极限位移降低。对于主筋40 mm 的桥墩，采用套筒连接后，塑性铰长度相比于整体现浇桥墩减小了70%，极限位移相较于整体现浇桥墩减小了约50%；对于主筋32 mm 的桥墩，采用套筒连接后，塑性铰长度相比于整体现浇桥墩减小了60%，极限位移相较于整体现浇桥墩减小了约45%；对于主筋20 mm 的桥墩，套筒连接桥墩的塑性铰长度对应减小了50%，极限位移降低了约40%。

相比于主筋20 mm 和主筋32 mm 的桥墩，主筋40 mm 桥墩中套筒对桥墩等效塑性铰长度和极限位移的影响程度更大，主要原因如下：1)对于主筋40 mm 的桥墩，采用的是直径为95 mm 的套筒，等效为同等面积的钢筋直径为64 mm，而主筋20 mm 的桥墩，采用的套筒直径为66 mm，等效为同等面积的钢筋直径为53 mm，套筒直径越大，自身刚度和面积就越大，对桥墩的变形影响程度越大。2)对于主筋40 mm 的桥墩，套筒连接段的长度大于其整体现浇桥墩的塑性铰长度，为整体现浇桥墩塑性铰长度的1.14 倍，而主筋20 mm桥墩的套筒连接段长度比其整体现浇桥墩的塑性铰长度小，仅为其整体现浇桥墩塑性铰长度的71%，这表明，将套筒预埋在桥墩塑性铰区域后，主筋40 mm 桥墩的塑性铰区域全被套筒覆盖，新的塑性区域主要位于墩底接缝区域，而主筋20 mm桥墩的塑性铰区域仍有部分未被套筒覆盖的混凝土段可以发生塑性变形，因此采用套筒连接后，主筋20 mm 桥墩的极限位移减小幅度相较于主筋40 mm 桥墩较小，表明不同的套筒直径，对于桥墩的极限位移影响程度不同，套筒直径越大，则套筒连接段越长，其对桥墩极限位移的减小幅度也就越大。表5 给出了主筋20 mm 工况下不同套筒长度桥墩对应的极限位移的有限元计算结果。由表中数据可以看出，当套筒直径相同时，桥墩预埋套筒长度越长，对桥墩极限位移的影响越大，桥墩极限位移减小越明显。

表5 不同套筒长度有限元极限位移计算结果 /mTable 5 Displacement capacities with different sleeve lengths calculated by finite element analysis

3.4.2 桥墩截面曲率和应变分布对比

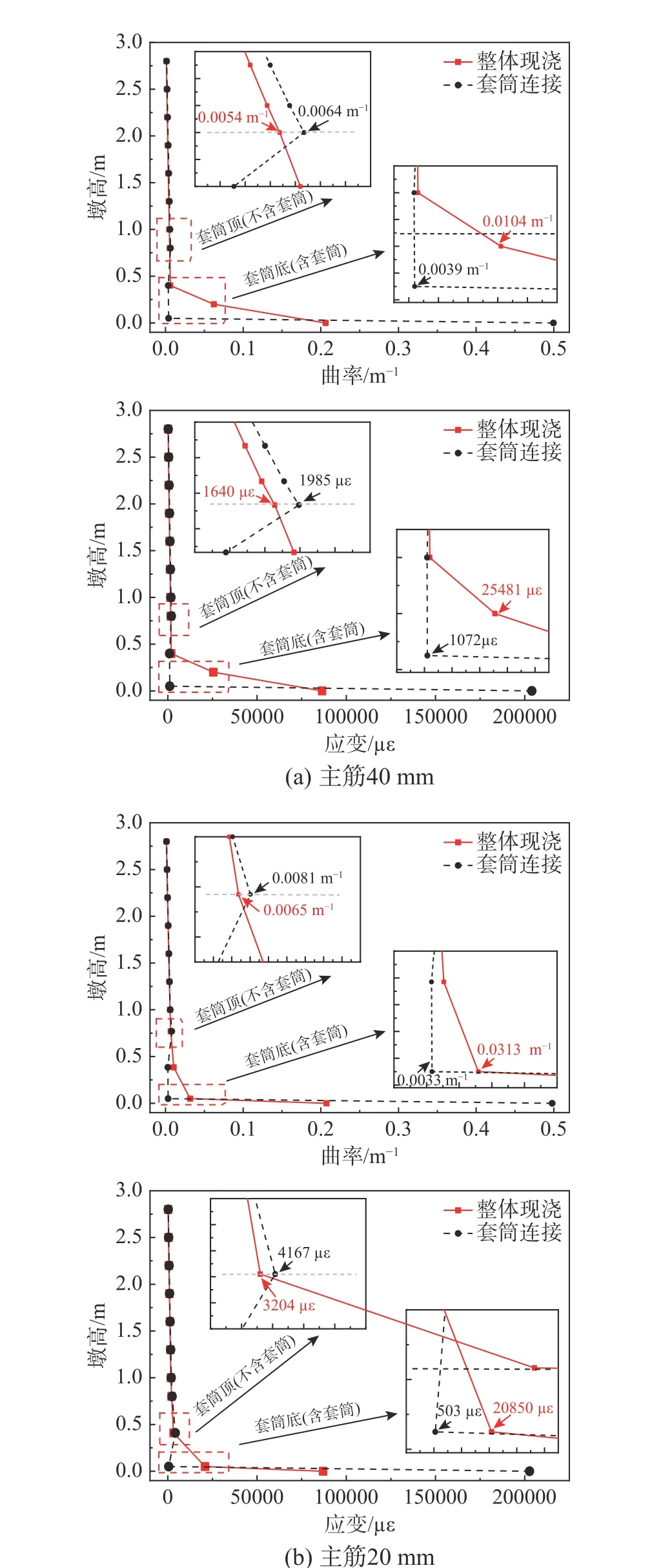
图19 有限元结果分布图Fig.19 Distribution diagram of finite element analysis results

利用有限元模型计算得到的墩身曲率和钢筋应变随墩高的分布情况，如图19 所示，主筋32 mm的分布图与主筋40 mm 的相似，本文仅给出钢筋直径40 mm 和20 mm 的作为比较。从图中可以看出，两个工况中，套筒连接桥墩和整体现浇桥墩的墩身曲率与钢筋应变分布相差较大，套筒段刚度、面积越大，曲率与应变越小，而在套筒的交界面处，即墩底接缝处和套筒顶位置，曲率增大且应变集中现象明显。

1)桥墩接缝处结果对比

表6 给出了主筋40 mm、主筋32 mm 和主筋20 mm 三种工况下，墩顶位移加载到150 mm 时，桥墩接缝处，整体现浇和套筒连接两个模型的曲率计算结果对比。从表中可以看出，无论主筋40 mm的桥墩还是主筋32 mm 和主筋20 mm 的桥墩，套筒存在后，均使接缝处的曲率值增大，但主筋40 mm桥墩的套筒对接缝处的影响稍大，相比于整体现浇桥墩，套筒的存在使接缝处的曲率扩大了2.42 倍，而主筋20 mm 的桥墩，套筒的存在使接缝处的曲率扩大了2.39 倍。表7 给出了主筋20 mm 工况下，不同套筒长度桥墩当墩顶位移加载到150 mm 时，桥墩接缝处的曲率计算结果对比。通过表中数据可以看出，套筒长度对接缝处的曲率有一定的影响，当套筒长度越长，接缝处曲率越大。

表6 不同套筒直径接缝处曲率结果对比 /m−1 Table 6 Comparison of curvatures at segmental interface of different sleeve diameters

表7 不同套筒长度接缝处曲率结果对比 /m−1Table 7 Comparison of curvatures at segmental interface of different sleeve lengths

表8 为主筋40 mm、主筋32 mm 和主筋20 mm三种工况下，墩顶位移加载到150 mm 时，桥墩接缝处整体现浇与套筒连接两个模型的钢筋应变计算结果对比。从表中可看出，钢筋应变的变化情况和曲率的变化情况一致，套筒的存在均增大了接缝处钢筋的应变值。对于主筋40 mm 的桥墩，套筒的存在使接缝处的钢筋应变扩大了2.36 倍，而对于主筋20 mm 的桥墩，扩大了2.32 倍，两者变化程度略有差异。表9 给出了主筋20 mm 工况下，不同套筒长度桥墩当墩顶位移加载到150 mm时，桥墩接缝处钢筋应变计算结果对比，其变化情况与曲率变化情况一致，套筒越长，接缝处钢筋应变越大。

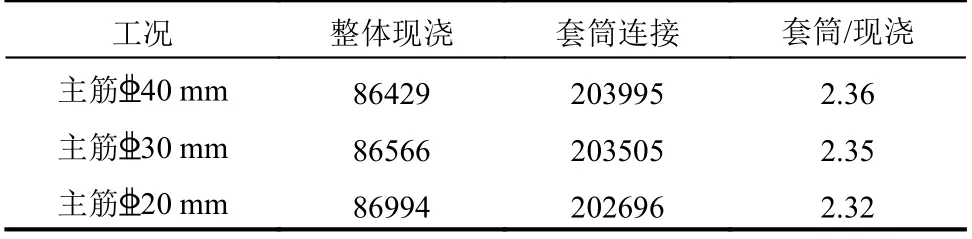
表8 不同套筒直径接缝处钢筋应变结果对比 /µεTable 8 Comparison of strains at segmental interface of different sleeve diameters

表9 不同套筒长度接缝处钢筋应变结果对比 /µεTable 9 Comparison of strains at segmental interface of different sleeve lengths

表10 不同套筒直径的套筒顶部位置(不含套筒)曲率对比 /m−1Table 10 Comparison of curvatures at top of sleeve with different sleeve diameters (excluding sleeve)

2)套筒顶部位置(不含套筒)结果对比

表10 给出了主筋40 mm、主筋32 mm 和主筋20 mm 三种工况下，墩顶位移加载到150 mm时，套筒顶部位置(不含套筒)，有无套筒两个模型的墩身曲率计算结果对比。从表中可以看出，无论主筋40 mm 的桥墩还是主筋32 mm 和主筋20 mm的桥墩，套筒存在后，交界面处刚度突变，均使套筒与非套筒段相连处的墩身曲率值增大，但主筋20 mm 桥墩在套筒顶部(不含套筒)处墩身曲率相比于整体现浇桥墩增大了30%，而对应的主筋40 mm 的桥墩，仅增大了17%，主筋20 mm 套筒桥墩的影响程度更大。因主筋20 mm 的套筒连接段长度小于其对应的整体现浇桥墩的塑性铰长度，所以在套筒连接段上方，仍有部分钢筋混凝土处于塑性铰区域，而主筋40 mm 的桥墩，套筒连接段长度大于整体现浇桥墩的塑性铰长度，套筒上方曲率增加相对较少。表11 给出了主筋20 mm工况下，不同套筒长度桥墩当墩顶位移加载到150 mm 时，套筒顶部位置曲率计算结果对比。从表中可以看出，套筒长度越长，其顶部曲率越小，当套筒长度增长到一定长度后，曲率增长趋于平缓。

表11 不同套筒长度的套筒顶部位置(不含套筒)曲率对比 /m−1Table 11 Comparison of curvatures at top of sleeve with different sleeve lengths (excluding sleeve)

表12 为主筋40 mm、主筋32 mm 和主筋20 mm三种工况下，墩顶位移达到150 mm 时，套筒顶部位置(不含套筒)，有、无套筒两个模型的钢筋应变计算结果对比。从表中可看出，钢筋应变的变化情况和曲率的变化情况一致，套筒的存在均增大了套筒顶部钢筋的应变值，且主筋20 mm 套筒的影响程度略大，表明不同套筒直径对套筒顶部的钢筋应变影响程度略有差别，但影响程度均远小于接缝处的影响程度。表13 给出了主筋20 mm工况下，不同套筒长度桥墩当墩顶位移加载到150 mm 时，套筒顶部位置钢筋应变计算结果对比，从表中可以看出，套筒长度越长，其套筒顶部钢筋应变越小。

表12 不同套筒直径的套筒顶部(不含套筒)钢筋应变对比 /µεTable 12 Comparison of strains at top of sleeve with different sleeve diameters (excluding sleeve)

表13 不同套筒长度的套筒顶部位置(不含套筒)钢筋应变对比 /µεTable 13 Comparison of strains at top of sleeve with different sleeve lengths (excluding sleeve)

4 结论

本文以灌浆套筒预埋于墩身的预制拼装桥墩为研究对象，通过拟静力试验和数值模拟分析得到以下结论：

(1)地震作用下，灌浆套筒连接的预制拼装桥墩受力性能与传统现浇桥墩不同，因套筒自身刚度较大，套筒连接段形成一个刚性区域，致使墩身曲率与钢筋应变发生重新分布，墩底接缝处应变集中现象明显。

(2)灌浆套筒预埋在墩底塑性铰区域时，因套筒刚度较大，套筒区域处在弹性状态，桥墩的等效塑性铰高度减小，从而灌浆套筒连接的预制拼装桥墩的极限位移减小。

(3)采用灌浆套筒连接的预制拼装桥墩模型拟静力试验结果表明，桥墩的破坏部位集中在墩底接缝处，套筒区域损伤较小，试件的最终破坏形式为墩底接缝处钢筋拉断，破坏时墩身混凝土损伤较小，验证了灌浆套筒受力机理的理论分析。

(4)通过有限元数值分析可知，灌浆套筒连接的预制拼装桥墩与整体现浇桥墩相比，弯曲变形能力降低，约为整体现浇桥墩的60%；在套筒段交界面处，墩身曲率和钢筋应变有所增加，其中墩底接缝处增加明显。

(5)套筒直径对桥墩接缝处的墩身曲率和钢筋应变影响较大。套筒直径越大，桥墩接缝处的墩身曲率和钢筋应变相比于无套筒情况增大越明显；而套筒直径对套筒顶部的墩身曲率和钢筋应变影响较小。

(6)套筒长度对桥墩接缝处的墩身曲率和钢筋应变的影响与套筒直径产生的影响相同。套筒长度越长，桥墩接缝处的墩身曲率和钢筋应变越大；而对于套筒顶部的墩身曲率和钢筋应变影响较小。