基于生存分析方法的公交站间行驶持续时间影响因素敏感性分析
2020-10-29张萌萌王立超
孙 芮, 张萌萌*, 王立超, 姜 震
(1.山东交通学院交通与物流工程学院, 济南 250357; 2.南京航空航天大学民航学院, 南京 210000)
公交站间行驶持续时间是周转时间的基本单元,是提高公交到站时间可靠性研究的关键参数。通过提高到站时间的可靠性,有利于吸引乘客选择公交出行方式,缓解城市交通拥堵。中外对站间行驶时间的研究方法主要集中在两方面,一是通过分析到站时间历史数据的规律提高公交到站时间预测精度,二是分析站间行驶持续时间中的相关因素预测到站时间。基于历史数据的研究如下:艾文文[1]通过归一化公交车辆GPS数据,采用长短期记忆(long short-term memory,LSTM)方法对公交到站时间进行预测。宋爽[2]将支持向量机与卡尔曼滤波相结合,首先基于历史数据,采用支持向量机对行程时间进行预测,接下来通过频数加权法预测各站点停靠时间,最后采用卡尔曼滤波对停靠时间进行调整。Yu等[3]建立了多线路支持向量机预测模型,通过将不同线路的车头时距、行程时间加权值以及同线路不同车辆行程时间的加权值输入模型,提高公交到站时间的精度。闫金金等[4]提出时间融合模型预测公交到站时间,选取公交线路中包含公交站牌和交叉口的部分路段作为研究对象,将动态路段行程时间和基于浮动车数据的路段行程时间相融合,消除预测值偏差,最终提高对到站时间的预测精度。胡华等[5]基于实时和历史的公交车辆自动定位数(AVL)需求分析,将公交车辆到站时间划分为站点停靠时间、区段全程运行时间和区段部分运行时间,分别采用点估计法、BP 神经网络法和自适应指数平滑法对其进行动态预测。关于站间行驶时间影响因素的研究:基于相关因素分析的研究如下:部分专家[6-11]从路段的平均车速、交叉口饱和度以及路段排队长度等方面出发,分析对公交行程时间的影响程度,建立公交行程时间可靠性预测模型。Peng等[12]将公交到站时间的影响因素,如:交通状况、天气等与公交车辆GPS数据相结合,利用LSTM方法进行到站时间预测,预测结果与传统模型相比,该模型的鲁棒性与预测精度具有明显提升。Chen等[13]将公交站数、站间距离、交通信号、天气、时间段、温度、能见度和出发时间8个因素作为自变量,建立了快速公交系统(BRT)公交到站时间回归预测模型。现有对高峰期、天气状况等突发事件下的公交到站时间研究较少,导致预测精度不理想;研究多是针对公交线路的周转时间,未详细考虑每个站点间的站间行驶持续时间与周转时间的关联性。现选用站间行驶持续时间作为研究对象,采用生存分析方法对其影响因素加以分析,以此判断各因素对站间行驶持续时间敏感度的高低,进而提高公交到站时间可靠性。
1 站间行驶持续时间模型
1.1 相关术语概念
(1)生存时间:广义的生存时间是指从某事件开始到结束所经历的时间跨度,本文生存时间T指公交车辆从第i站到第i+1的站间行驶持续时间(下文统称“持续时间”)。
(2)起点事件:起点事件是能够反映研究对象在生存过程中起始特征的事件,本文起点事件是公交车在第i站开始发车的时刻。
(3)终点事件:终点事件又称死亡事件,是指研究者所关心的特定结局,本文事件的终点是车辆到达第i+1站的时间。
(4)右删失数据:存在持续时间T和时间Cr,如果T>Cr,则时间Cr称为右删失数据,数据的状态是“生存”。本文右删失数据相当于持续时间的到站可靠性高。
(5)到站时间可靠性:到站时间可靠性指公交车辆到站的准时性,影响坚持在车站上等待公交车到来的乘客数量,也影响乘客每天到达某一目的地时间的一致性[14]。
(6)到站时间可靠性阈值:到站时间可靠性阈值是判别持续时间生存或死亡状态的依据,检测公交到站可靠性的高低。若持续时间在阈值范围内,状态视为“生存”,公交到站时间可靠,反之视为“死亡”,公交到站时间不可靠。假设线路某时段计划发车m辆,周转时间Tr,发车间隔Fr,使发车的车辆能够做首尾相接,到站时间可靠性阈值范围公式为:
(1)
式(1)中:Fr为某时段内某线路公交车辆的计划发车间隔,s;Tr为某时间段内某线路中一辆公交车的实际周转时间,s。
1.2 持续时间的概率密度函数
持续时间的概率密度函数是度量死亡可能性函数,也称危险函数,其数学表达式为
(2)
(3)
式中:f(t)为持续时间t的死亡概率;S(t)为持续时间的死亡函数;Di为持续时间为死亡状态下的到站延误时间;Ni为实际持续时间与拟定持续时间的时间差绝对值。
1.3 持续时间的生存函数
持续时间生存函数的数学表达式为

(4)
式(4)中:P(T≤t)为持续时间的生存函数,持续时间下的生存时间不大于某时刻t的概率。
1.4 持续时间的死亡函数
持续时间死亡函数的数学表达式为
S(t)=P(T>t)=1-F(t)=

(5)
式(5)中:S(t)为持续时间的死亡函数,表征持续时间超过时间t的概率分布。
2 基于K-M估计的单个影响因素敏感性分析
由于生存时间函数分布形式的不确定性,选用非参数方法估计。非参数方法根据样本提供的顺序统计量能对生存率进行估计,常用的方法有乘积极限法和生命表分析法。由于生命表分析法需将样本数据分成k+1个等距的小区间,而站间行驶时间是不等的区间段,在此不适用,故而选择用乘积极限法进行分析。乘积极限法是由Kaplan和Meier首先提出的,又称为K-M估计。根据实际数据计算不同时间的生存概率,然后采用条件概率及概率乘法的原理计算生存率,所以被称为乘积极限法。
对于站间行驶持续时间,当车辆到达停靠站,而到站时间可靠性在阈值接受范围之内,则该站间行驶持续时间的状态为生存,该站间行驶持续时间为右删失数据。
采用K-M法时对总体W的n个数据进行观测,n是包含所有删失数据和非删失数据的总数,ti为死亡数据时,令δi=1;当ti是右删失数据时,令δi=0,所以所得到的数据可记为(ti,δi)(i=1,2,…,n)。
首先每站的站间行驶持续时间的寿命时间按从小到大进行排序(当一个删失数据和一个死亡数据相等时,将死亡数据排在删失数据之前[15])t1 (6) 对义乌市803号公交线路经过现场调研与分析,进行早高峰运营数据调取,得到该线路的到站时间可靠性阈值:0 基于义乌市803号公交线路数据,将不同天气状况对站间行驶持续时间的敏感度进行分析,分析结果如图1所示。 图1 不同天气状况下站间行驶持续时间生存和危险函数Fig.1 Inter-station driving duration survival and dangerous function under different weather conditions 曲线1表征关键因素影响下的累积生存函数曲线或累计危险函数曲线;曲线0表征无关键因素影响下的累计生存函数曲线或累计危险函数曲线。由图1可知,有天气状况影响的持续时间生存曲线与危险曲线斜率大。检验统计量的方法有:对数秩法、Breslow法和Tarone-Ware法。由于Breslow检测法会依据每一个时间点上的危险观测数来给予每一个时间点的不同权重,然后检验生存分布是否相等[16]。而在线路上每一时刻都会有不同的因素影响到站时间可靠性,所以在此选用Breslow检验法来检验统计量。根据Breslow检验法来判断不同的天气状况对持续时间是否有影响,计算得出:Sig=0.01。其中,Sig为显著性水平,当Sig<0.05表明差异性显著,说明天气状况对持续时间的影响是显著的。 将不同拥堵状况对站间行驶持续时间的敏感度进行分析,分析结果如图2所示。 图2 不同拥堵状况下站间行驶持续时间生存和危险函数Fig.2 Inter-station driving duration survival and dangerous function under different congestion conditions 由图2可知,公交的持续时间在0~200 s内发生了拥堵,由于存在右删失数据,可判断此时到站可靠性高;在350 s的节点生存曲线下降梯度大,危险曲线上升锑度大,持续时间受到第二次拥堵的干扰。伴随着第二次拥堵的发生,持续时间已超出可靠性阈值范围,到站时间可靠性低。每一次拥堵发生,生存曲线梯度下降,危险曲线梯度上升。根据Breslow检验法来判断不同拥堵状况对持续时间是否有影响,计算得出:Sig=0.03<0.05,差异性显著,说明不同拥堵状况对持续时间的影响是显著的。 将不同上下车人数对站间行驶持续时间的敏感度进行分析,分析结果如图3所示。 图3 不同上下车客流量站间行驶持续时间生存和危险函数Fig.3 Inter-station driving duration survival and dangerous function under passenger flow getting on and off 曲线0表征上下车客流量在0~15 人的累计生存函数曲线或累计危险函数曲线,曲线1表征上下车客流量在16~30 人的累计生存函数曲线或累计危险函数曲线。由图3可知,持续时间在400~650 s内上下车人数较多,生存曲线与危险曲线斜率大,走向大体一致。根据Breslow检验法来判断上下车客流量对持续时间是否有影响,计算得出:Sig=0.015 7<0.05,差异性显著,说明上下车客流量对公交到站时间的影响是显著的。 设X=(X1,X2,…,Xk)是影响持续时间t的k个风险因素,设h(t,x)表示受危险因素x的影响下,在时刻t的风险函数,则有: h(t,X)=h0(t)exp(β1X1+β2X2+…+βpXp) (7) 式(7)中:t是周转时间的基本单元持续时间;x是不随时间而改变的协变量;β=(β1,β2,…,βp)是回归系数向量;h0(t)为基准风险函数,是与时间有关的任意函数,它是全部协变量都为0即没有其他影响因素的作用下,在t时刻的风险函数。表1为站间行驶持续时间影响因素及赋值表。 在n个持续时间的样本数据中,按从小到大的顺序依次排列:t1 表1 站间行驶持续时间影响因素及赋值表Table 1 Table of influencing factors and assignment of inter-station driving duration 时间ti处的风险集,R(ti)由生存时间不小于ti(到站时间可靠性阈值)的个体组成,即到站时间大于ti的时间内的集合。风险集内时间ti开始死亡的事件,这一事件结束的概率为 (8) 将所有到站时间相乘得到偏似然函数: (9) 对偏似然函数两边取对数,可得到对数似然函数: (10) 对对数似然函数求极大似然估计量后,再求β的偏导数,就可以求出β的最大似然估计量。 根据比例风险模型,将不同天气状况、道路拥堵状况与不同上下车客流量等因素对站间行驶持续时间的影响综合分析,结果如图4所示。 图4 综合因素影响下的站间行驶持续时间生存和危险函数Fig.4 Inter-station driving duration survival and dangerous function under the influence of comprehensive factors 持续时间由于因素的干扰,会随着行驶时间的延长而增大。由图4可以看出在0~400 s,生存率为1,虽然此区间的持续时间有影响因素的干扰,但是到站时间可靠性还有一定承载能力,故此区间的到站时间可靠性高;400~800 s的寿命区间中,生存与危险曲线斜率大,说明有外在因素的干扰导致持续时间延长,到站时间可靠性降低。 根据比例风险回归模型对协变量进行极大似然参数估计,结果如表2所示。 表2 基于比例风险回归模型参数估计结果表Table 2 The result table of parameter estimation based on proportional hazards model model B为模型系数;SE为回归系数标准差;Wald用于检验回归系数与0 有无显著性差异;exp(β)为胜算比值,表示该协变量每增加一个单位,时间持续时间危险率变化的倍数。故根据表2,公交车到站时间的危险函数为 h(t,x)=h0(t)exp(-3.34X1-0.205X2+ (11) 拥堵状况、天气状况与上下车人数较多时的回归系数为负,其相对危险度分别降低了1-0.227=0.773(倍)、1-0.815=0.185(倍)和1-0.248=0.752(倍),协变量越小,持续时间在此因素下到站可靠性高的概率小,说明该因素对持续时间的敏感度越高。上下车人数较少时的回归系数为正,其相对危险度[exp(β)]为2.410(倍),协变量越大,持续时间在此因素下保持到站可靠性高的几率大,说明该因素对持续时间的敏感度不高。根据协变量的大小加之以上的分析,本文研究的三因素对持续时间的敏感度由大到小排列分别是:拥堵状况、天气状况、上下车客流量随着人数的增加,敏感度随之增高。 由于中外对到站时间可靠性评价体系[17-19],多是分析车辆运行时间与期望运行时间的绝对差值,进而判断到站时间可靠性。在此,选择义乌市803号线路进行实例分析,选用公交到站可靠性作为评价指标,对本文采用生存方法下的风险回归模型与以往研究常规公交到站时间可靠性模型进行对比评价。常规公交到站时间可靠性综合评价模型为 (12) 式(12)中:Si为公交车辆在站点i的到站时间可靠性;Tsi为公交车辆在站点i与上一站间的实际运行时间;Tei为公交车辆在站点i与上一站间的期望运行时间;δ1、δ2为运行时间绝对差的极大值与极小值。 由公交运行信息可知,锈湖中学附近路段出现拥堵,成龙集团站点与义乌英菲尼迪站点至火车站站点的上下车客流较大。通过采用风险回归模型与以往研究到站时间可靠性模型进行计算,得到803号线路各个站点可靠性,具体结果如表3所示。 表3 803号线路在不同方法下的可靠性Table 3 Station reliability of line 803 under different methods 由表3可知,该条线路中站点可靠性波动较大。其中,以下站点的风险回归模型可靠性低于以往研究模型下的可靠性:川纳服饰鄂尔多斯站点至丹溪二小区站点、成龙集团站点与嘉德莱集团站点、义乌英菲尼迪站点至火车站站点;其余站点的可靠性在两种方法的分析下相差不大。由于锈湖中学附近路段拥堵,造成该区域的公交到站可靠性骤然下降,表明了风险回归模型对该影响因素的敏感性较高;成龙集团站点、义乌英菲尼迪站点至火车站站点的上下车客流量较大,在风险回归模型中对公交到站可靠性有较为直观的影响。 通过以上研究可知,采用生存方法下的风险回归模型不仅能够计算线路中各个站点行程时间的可靠性,分析各站点可靠性波动的大小,而且基于公交到站时间的可靠性,分析影响公交行程时间因素的敏感度高低,从而对公交到站时间精准预测提供理论支撑。 针对公共交通周转时间的随机性,将周转时间划分为逐个站间行驶持续时间的单元,提高了对每个单元稳定性与能控性等定性分析能力。生存分析方法,能够定量解释各个变量的时间变化特性。本研究构建了公共交通站间行驶持续时间模型,将到站时间可靠性阈值作为判定站间行驶持续时间生存状态的依据,并利用大量的实测数据,通过Kaplain-Meiei方法与比例风险回归模型对重要影响因素进行分析,定量的表征了各影响因素对站间行驶持续时间生存状态的因果关系,主要结论如下: (1)通过Kaplain-Meiei方法分析,单独比较不同因素下站间行驶持续时间的生存率与死亡率,结果表明:天气状况、道路拥堵状况以及上下车人数对站间行驶持续时间有显著影响,敏感度较高。 (2)通过建立比例风险回归模型,针对天气状况、道路拥堵状况及上下车客流量这三类因素,综合分析对站间行驶持续时间的影响程度。结果表明:拥堵状况、天气状况和上下车客流较多时,到站可靠性差,对站间行驶持续时间的影响显著,敏感度高;上下车人数较少时,到站可靠性在可接受范围内,敏感性低。 (3)文中所分析的影响站间行驶持续时间的因素主要是三大类(天气状况、拥堵状况、以及上下车人数),然而影响因素不止局限于这三类,比如交通服务质量、交通政策等也是影响变量。在未来研究中,将这些因素纳入模型,以求提高到站可靠精度,精准的预测公共交通周转时间提供一定的数据和理论支撑。2.1 不同天气状况对站间行驶时间的影响
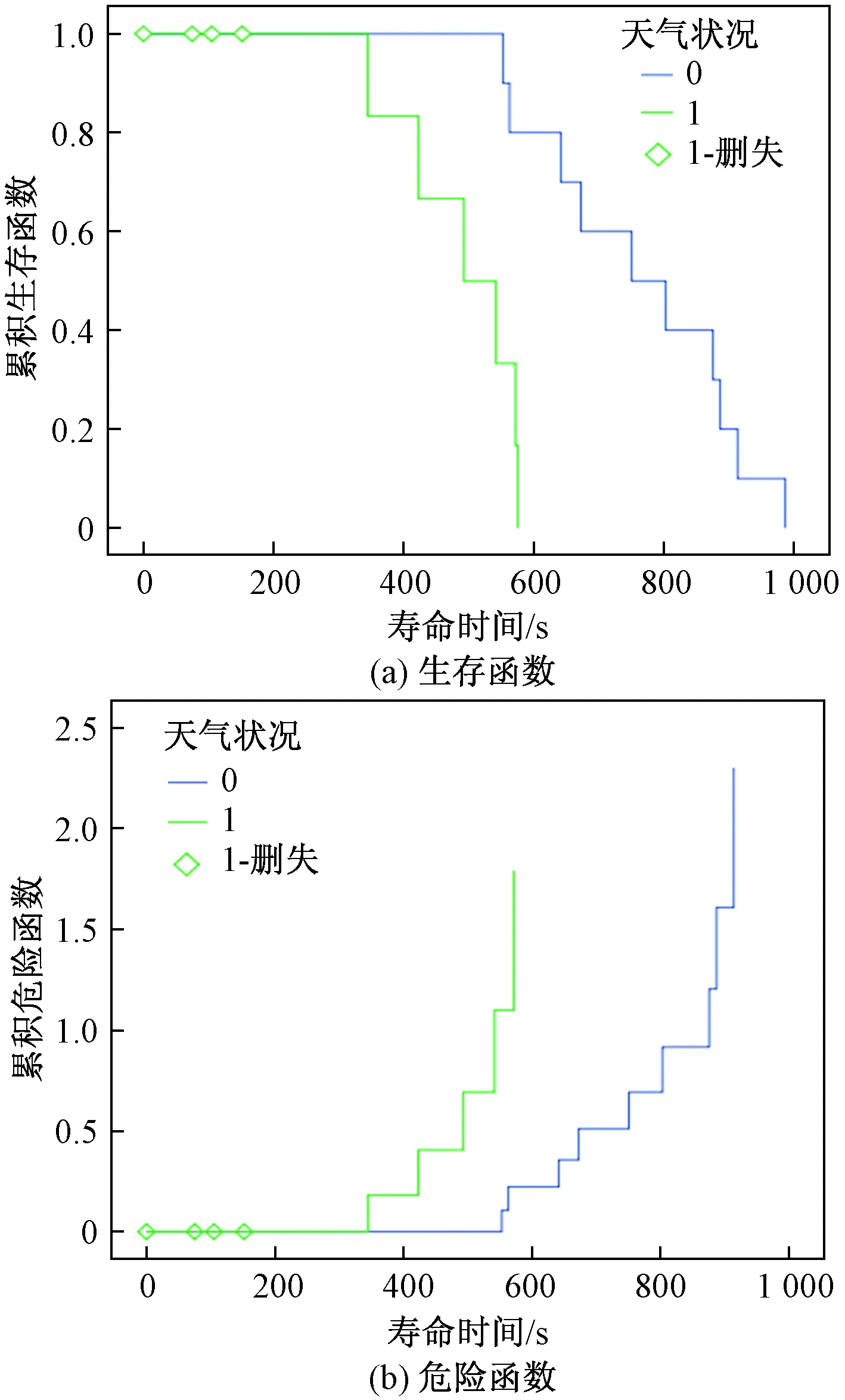
2.2 不同拥堵状况对站间行驶时间的影响

2.3 不同上下车人数对站间行驶时间的影响

3 基于比例风险回归模型的影响因素综合评价
3.1 比例风险模型的参数估计





3.2 比例风险回归模型综合评价
3.3 实例分析

4 结论
