高超声速滑翔飞行器滑翔段初始状态的唯一性和最优性分析*

孟繁卿，田康生

(1. 空军预警学院 研究生大队， 湖北 武汉 430019； 2. 空军预警学院 预警情报系， 湖北 武汉 430019)

临近空间高超声速滑翔飞行器通常是指飞行马赫数大于5、在距地面20～100 km的高度依靠空气动力滑翔的一种飞行器。临近空间高超声速滑翔飞行器的显著特点是飞行高度比弹道导弹低，飞行速度远高于普通航空飞行器。因此高超声速滑翔飞行器兼具弹道导弹的高速、航空飞行器的灵活机动的特点，被视为改变战争规则的“撒手锏”武器。高超声速滑翔飞行器可多次变轨，其弹道大部分为滑翔段，而滑翔段的弹道特性除受控制律控制外，主要受滑翔段初始状态影响。

文献[1]针对平衡滑翔弹道对初始状态精度要求高的特点，设计了基于预测校正的制导律，增强了平衡滑翔弹道对初始状态的鲁棒性。文献[2]利用正则摄动的方法得出了高超声速滑翔飞行器平稳滑翔的解析解，分析了平稳滑翔弹道的动态特性。文献[3-5]以射程最大、能量最省、总气动加热最小等为优化目标，分析了不同飞行器初始状态以及飞行器升阻比等气动参数对弹道的影响，指出飞行器弹道特性主要受飞行器初始状态影响。文献[6-7]利用高斯伪谱法，分别从燃料最省和航路规划的角度对高超声速飞行器的轨迹进行了优化。文献[8]利用物理规划和遗传算法，求解了射程最大、约束变量最小、弹道最稳定的优化弹道。文献[9]利用模式搜索算法对高超声速飞行器轨迹进行优化，分析约束条件对飞行器轨迹和弹道的影响，为确定飞行器的初始状态提供了参考。文献[10-11]指出跳跃滑翔弹道的初始状态决定了飞行器的飞行能力，用分段高斯伪谱法对多约束条件下的滑翔弹道进行了优化。文献[12]从雷达跟踪精度的角度对跳跃滑翔弹道的突防性能进行了分析，得出了弹道的机动性能越强、飞行器的突防性能越优的结论。文献[13]利用正交试验分析了初始状态对跳跃滑翔弹道机动性能的影响，通过回归分析估计了机动性能最优时的滑翔段初始状态。

以上文献的研究主要集中于平衡滑翔弹道的弹道特性分析以及跳跃滑翔弹道的控制律优化设计，尚缺乏滑翔段初始状态对弹道特性影响规律的研究。因为高超声速滑翔飞行器是一种无动力飞行器，滑翔段初始状态对飞行器滑翔段的飞行能力和弹道特性至关重要，所以有必要研究滑翔段初始状态对高超声速滑翔飞行器弹道特性的影响规律。

1 高超声速滑翔飞行器滑翔段运动模型

1.1 飞行器滑翔段运动方程

根据高超声速滑翔飞行器在滑翔段的受力情况，建立速度和位置的四自由度运动方程，如式(1)所示。式中，V是飞行器飞行速度，γ是速度倾角，(x,z)是飞行器在纵向平面内的位置坐标，m是飞行器质量，g0是重力加速度常数，L是飞行器所受升力，D是飞行器所受阻力。

(1)

其中升力、阻力的计算可由式(2)求得。ρ为大气密度，如式(3)所示，在此采用指数模型计算飞行器所在飞行高度的大气密度，ρ0=1.225 kg/m3为海平面大气密度常数，ξ=8434 m为高度常数；S是飞行器的参考面积；CL和CD为飞行器升力系数、阻力系数[14]。

(2)

(3)

1.2 滑翔段弹道控制参数模型

1.2.1 纵向平衡滑翔弹道控制参数模型

飞行器纵向平衡滑翔时，在纵向平面内受力平衡，速度倾角变化率为零(如式(4)所示)，又因为飞行器在纵向平面内的主要控制参数是攻角α，所以令飞行器攻角保持不变、同时满足速度倾角变化率为零的限制条件[8]，即可实现临近空间高超声速滑翔飞行器的纵向平衡滑翔。

(4)

1.2.2 纵向跳跃滑翔弹道控制参数模型

控制临近空间高超声速滑翔飞行器在纵向平面内跳跃运动的主要参数是攻角α，纵向跳跃滑翔弹道控制参数模型即攻角α参数模型[15]，如式(5)所示。

(5)

式中，αmax为最大飞行攻角，αKmax为最大升阻比攻角，V1和V2分别为攻角参数变化的两个临界速度。

2 纵向平衡滑翔初始状态唯一性分析

2.1 飞行器状态解析解

由平衡滑翔条件，将式(2)代入式(4)整理可得：

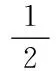
(6)

所以可推导出飞行器速度表达式为：

(7)

将式(3)代入式(7)整理可得：

(8)

式(8)对z求微分可得：

(9)

将式(8)代入式(9)可得：

(10)

将式(1)代入式(10)可得：

(11)

由式(10)和式(11)可得：

(12)

将式(2)、式(7)代入式(12)整理可得：

(13)

由式(13)可得飞行器速度V的解析式：

(14)

由式(7)和式(14)可得：

(15)

由式(3)和式(15)可得：

(16)

2.2 初始状态唯一性分析

令V=f(γ)，对式(14)求导可得：

(17)

由式(17)可知f′(γ)>0，所以f(γ)为γ上的单调递增函数。因为f(γ)为单调递增函数，所以f-1(V)一定存在，且和f(γ)单调性一致。

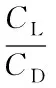
(18)

由f-1(V)与f(γ)单调性一致可得，γ>f-1(Vmin)，当取Vmin=1700 m/s时，可得f-1(Vmin)=-2.084°，又因为文献[15]已经证明γ为负的小量，所以可将γ的取值范围缩小为γ∈(-2.084°,0°)。

令z=g(γ)，C1=ρ0ξSCL，C2=ρ0ξSCD，对式(16)求导并整理可得：

(19)

令h(γ)=C1sinγ+C2cosγ可得：

(20)

将C1、C2代入式(20)可得：

(21)

由文献[15]可知5°≤α≤25°，所以可得：

(22)

因为γ∈(-2.084°,0°)，所以可得h(γ)>0。将式(20)代入式(19)可得：

(23)

由式(23)可知g′(γ)<0，所以g(γ)为γ上的单调递减函数。又因为f(γ)为γ上的单调递增函数，所以对初始状态(V0,γ0,z0)，只要确定三个初始量中的一个量，其余两个也唯一确定。当飞行器滑翔段初始状态(V0,γ0,z0)满足解析式(14)和式(16)时，飞行器才会以平衡滑翔弹道滑翔，否则只能以近似平衡滑翔弹道滑翔，或产生大幅度震荡以跳跃滑翔弹道滑翔。

2.3 仿真校验与分析

2.3.1 仿真设置

以美国洛克希德·马丁公司开发的高超声速通用气动飞行器CAV-H为例，对平衡滑翔弹道滑翔段初始状态分析进行验证。CAV-H飞行器质量为907.2 kg，参考面积为0.483 9 m2。取目标点位置(2×106m，-100 m)，αKmax=12°，x0=0 m。由式(14)和式(16)确定飞行器在45 km高度的平衡滑翔初始状态V0=3563 m/s，γ0=-0.247 2°，z0=-45 000 m。

为分析纵向平衡滑翔时滑翔段初始状态中各变量对弹道特性的影响，利用单因素敏感性分析方法对平衡滑翔弹道滑翔段的初始状态进行敏感性分析。如表1所示，设计了三组仿真实验进行对比：①保持(V0,γ0)不变，改变初始高度z0；②保持(γ0,z0)不变，改变初始速度V0；③保持(V0,z0)不变，改变初始速度倾角γ0。

表1 弹道0和三组对比弹道的滑翔段初始状态

2.3.2 弹道轨迹分析

图1是弹道0和三组对比弹道的弹道轨迹仿真。对比图1(a)、图1(b)、图1(c)可知，当初始高度、初始速度倾角偏离初始状态真值时，相应弹道都会围绕平衡滑翔弹道上下小幅度跳跃，跳跃幅度越来越小、逐渐收敛于平衡滑翔弹道，且图1(c)中三个弹道的波动幅度小于图1(a)中三个弹道的波动幅度。当初始速度偏离平衡滑翔初始速度真值时，第二组三个弹道在平衡滑翔弹道上方跳跃，且与平衡滑翔弹道的偏差越来越大。从三组对比仿真可知，初始速度偏离平衡滑翔初始速度真值对平衡滑翔弹道轨迹影响最大，初始速度倾角偏离平衡滑翔初始速度倾角真值对平衡滑翔弹道轨迹影响最小。

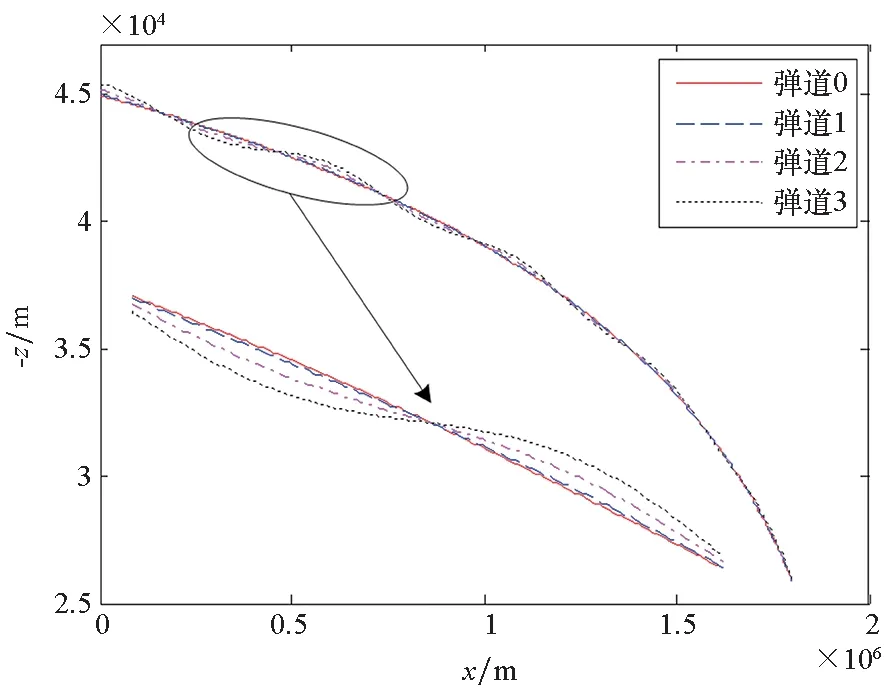
(a) 弹道0和第一组弹道的弹道轨迹仿真图

2.3.3 飞行速度误差分析

图2是三组对比仿真弹道的飞行速度与弹道0飞行速度的误差曲线图。对比图2(a)、图2(b)、图2(c)可知，第二组三个弹道的初始速

(a) 弹道0和第一组弹道的飞行速度误差

度偏离平衡滑翔初始速度真值时，相应弹道的速度误差最大，同时飞行过程中，速度误差曲线降低的趋势并不明显。第三组三个弹道的初始速度倾角偏离平衡滑翔初始速度倾角真值时，对弹道的速度误差影响最小，虽然第三组的速度误差曲线呈现收敛于非零值的趋势，但其速度误差数值在三组对比仿真中最小。

2.3.4 速度倾角误差分析

图3是三组对比仿真弹道的速度倾角与弹道0速度倾角的误差曲线图。对比图3(a)、图3(b)、图3(c)可知，第二组三个弹道的初始速度偏离平衡滑翔初始速度真值时，相应弹道的速度倾角误差介于第一组和第三组之间，但第二组三个弹道的速度倾角误差曲线呈现发散、不断变大的趋势。第三组三个弹道的初始速度倾角偏离平衡滑翔初始速度倾角真值时，对弹道的速度倾角误差影响最小，其速度倾角误差曲线呈现不断下降的趋势，且速度倾角误差数值最小。

(a) 弹道0和第一组弹道的速度倾角误差

2.3.5 飞行高度误差分析

图4是三组对比仿真弹道的飞行高度与弹道0飞行高度的误差曲线图。对比图4(a)、图4(b)、图4(c)可知，第二组三个弹道的初始速度偏离平衡滑翔初始速度真值时，相应弹道的高度误差与第一组大致相当，均高于第三组，但第二组三个弹道的高度误差曲线振荡发散、误差数值不断变大。第三组三个弹道的初始速度倾角偏离平衡滑翔初始速度倾角真值时，其高度误差曲线振荡收敛，弹道高度误差数值在三组对比仿真中最小，对弹道高度误差影响最小。

(a) 弹道0和第一组弹道的飞行高度误差

3 纵向跳跃滑翔初始状态最优性分析

3.1 最优性问题描述

由前文分析可知，飞行器滑翔弹道产生跳跃的原因是初始状态不满足平衡滑翔条件，即跳跃滑翔弹道滑翔段的初始状态不唯一。正是因为跳跃滑翔弹道滑翔段初始状态不能唯一确定，所以有必要对其初始状态的最优性进行研究，即寻找跳跃滑翔弹道滑翔段的最优初始状态。在此以飞行弹道的弹道性能最优为目标，初始状态最优性的数学模型如下：

弹道性能：f(V0,γ0,z0)

约束条件：

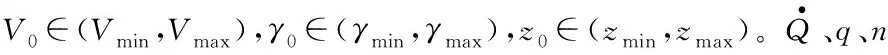
由初始状态最优性的数学模型可知，求解最优的初始状态为多约束条件下的优化问题。为便于问题求解，引入惩罚函数，将有约束优化问题转化为无约束优化问题，如式(24)所示，为弹道性能函数f(V0,γ0,z0)引入惩罚因子pi(i=1,2,…,5)。当滑翔弹道不满足约束条件时，需要在相应弹道的性能函数上叠加惩罚因子。

(24)

3.2 评价指标

为了评价以不同初始状态进行跳跃滑翔时的弹道特性，特选择以下几个评价指标。

1)机动变轨次数：机动变轨次数Nm定义为飞行器纵向加速度符号发生变化的次数。高超声速滑翔飞行器的弹道上下跳跃，所以无法像弹道导弹一样反推导弹的发射点和预测导弹的落点。机动变轨次数是高超声速滑翔飞行器机动性能的重要体现，机动变轨次数越多，飞行器弹道越灵活多变。

2)首跳高度：首跳高度ΔH是指飞行器第一次跳跃时的高度大小，其数值等于滑翔段初始位置与弹道轨迹曲线第一个极值点(极大值或极小值)之间的高度差。因为无法准确定义跳跃滑翔弹道的平衡位置，且随着飞行速度的下降，飞行器的跳跃幅度越来越小，所以采用首跳高度来衡量高超声速滑翔飞行器弹道的跳跃强度。

3)飞行时间：飞行时间ΔT是指飞行器滑翔段初始时刻与滑翔段结束时刻的差值。飞行时间越短，飞行器暴露在雷达、卫星等探测装备探测区的时间越短，越不容易被发现。即便被探测装备发现，因为飞行时间短，留给拦截武器的时间将被大大压缩，也将极大提高飞行器的生存能力。

4)剩余机械能：剩余机械能Ef是指滑翔段结束时刻高超声速滑翔飞行器总的机械能。高超声速滑翔飞行器在滑翔段做无动力滑翔，所以飞行过程中其机械能是不断减小的。滑翔段剩余机械能即飞行器末段的最大机械能。飞行器的剩余机械能越大，则为末段弹道提供的可利用能量空间越大。

综合以上评价指标以及约束条件，可确定求解最优初始状态时的目标函数，如式(25)所示。其中ω1、ω2、ω3、ω4分别为四个评价指标的指标权重，可通过本征向量法确定各评价指标的指标权重值为(0.472 9，0.169 9，0.284 4，0.072 8)。

f(V0,γ0,z0)=max(ω1Nm+ω2ΔH+

(25)

3.3 粒子群算法

粒子群算法是一种全局迭代搜索算法，该算法将优化问题的解看作是搜索空间中的粒子。算法起始时，随机产生种群大小为Npso的初始粒子群，即初始解集。在每次迭代中，利用目标函数计算粒子的适应度值，并更新粒子个体最优解和粒子群全局最优解。两个最优解更新完毕后，按照式(26)更新各粒子的速度和位置，实现粒子在解空间的局部搜索和全局搜索。当算法达到终止条件时，迭代结束并输出搜索结果。

(26)

式中，vj(t)为第t次迭代后粒子的速度，wpso为搜索惯性权重，C1pso和C2pso为学习因子，r1(t)、r2(t)为介于0和1之间的随机数，pj(t)为第t次迭代后粒子的个体最优解，g(t)为第t次迭代后粒子群的全局最优解，zj(t)为第t次迭代后粒子的位置。

3.4 仿真校验与分析

3.4.1 仿真校验

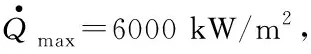
通过粒子群算法可求得最优的初始状态(V0,γ0,z0)为(4864.718 m/s，-4.727 8°，-93 691.965 m)，机动变轨次数Nm=12，首跳高度ΔH=53.181 km，飞行时间ΔT=1085 s，剩余机械能Ef=4.711×108J，目标函数值f(V0,γ0,z0)=0.568 3。

为分析纵向跳跃滑翔弹道滑翔段最优初始状态中各变量对弹道特性的影响，利用单因素敏感性分析方法对跳跃滑翔弹道滑翔段的最优初始状态进行敏感性分析。如表2所示，设计以下三组对比实验：①在最优的初始速度和速度倾角(V0,γ0)条件下，改变初始高度z0；②在最优的初始速度倾角和高度(γ0,z0)条件下，改变初始速度V0；③在最优的初始速度和高度(V0,z0)条件下，改变初始速度倾角γ0。

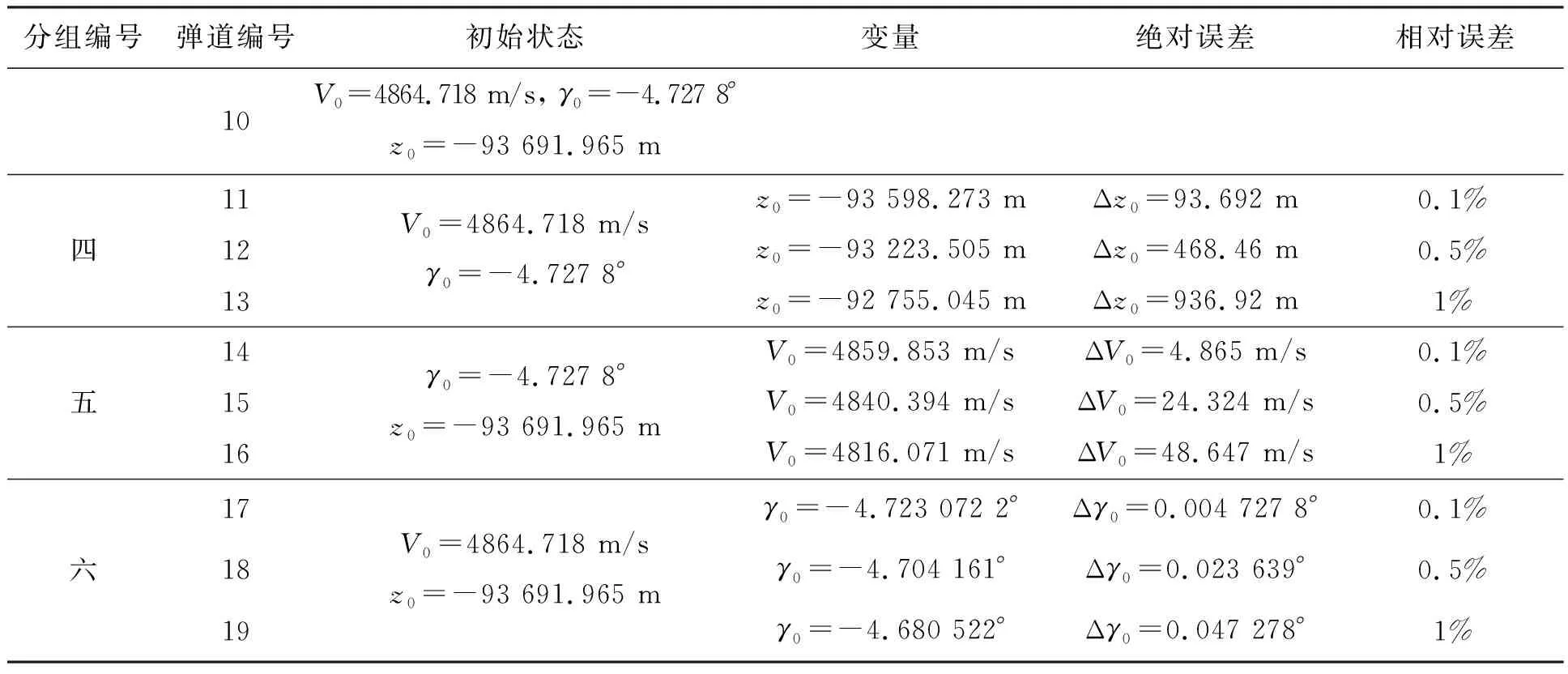
表2 弹道10和三组对比弹道的滑翔段初始状态

三组对比实验以及最优初始状态对应弹道的性能指标值和目标函数值如表3所示。由表3可知，最优初始状态的目标函数值最大，第五组三个弹道的目标函数值最小。下面从弹道轨迹和纵向加速度两个方面对三组弹道和最优初始状态对应弹道的弹道特性进行分析。

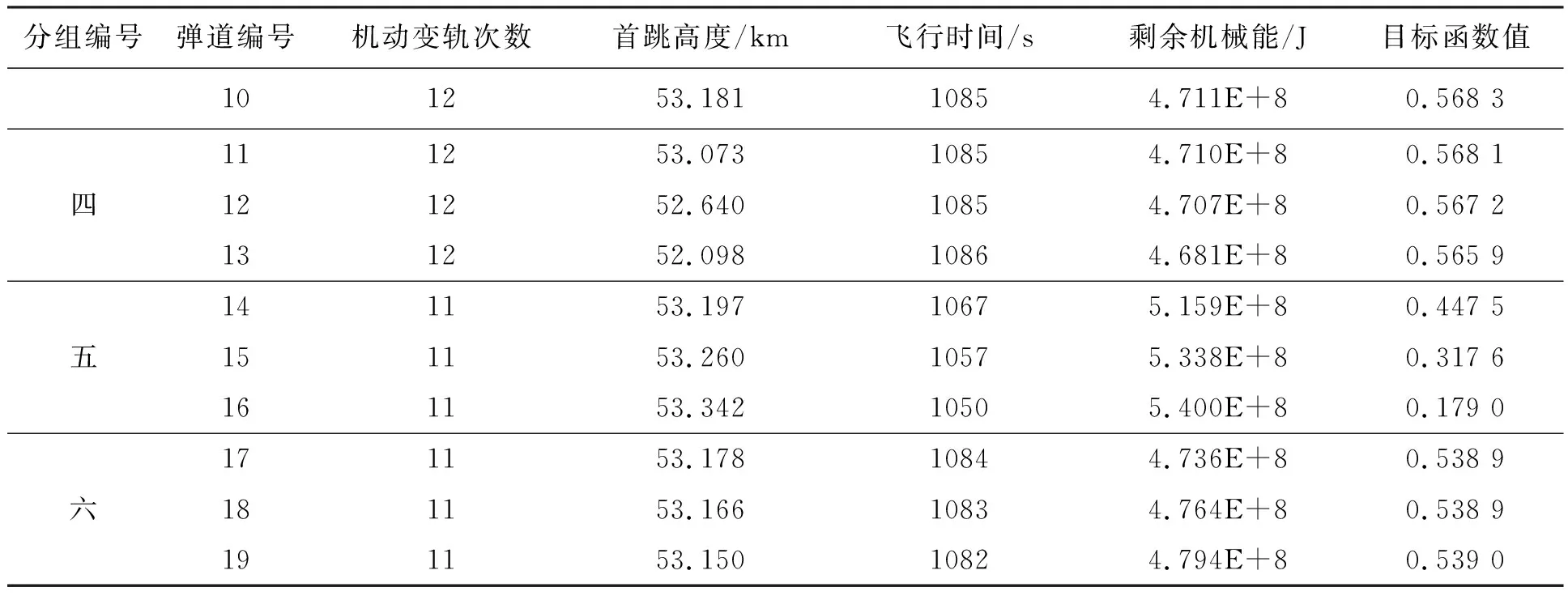
表3 弹道10和三组对比弹道的评价指标值和目标函数值

3.4.2 弹道轨迹分析

图5是三组对比弹道和弹道10的弹道轨迹仿真图。从图5(a)中可以看出，当初始高度偏离最优初始高度时，弹道的首跳高度会相应降低，且偏离程度越大，首跳高度越小。从图5(b)中可以看出第五组的三个弹道，滑翔段终点距离目标点的终端距离大于200 km，不满足终端约束。虽然第五组三个弹道的性能指标，除机动变轨次数外均优于弹道10的性能指标，但因为第五组的三个弹道不满足终端约束条件，所以第五组三个弹道初始状态的目标函数值明显低于其他两组弹道和弹道10初始状态的目标函数值。从图5(c)中可以看出，当初始速度倾角偏离最优初始速度倾角时，弹道的首跳高度会相应降低，且偏离程度越大，首跳高度越小。

对比图5(a)、图5(b)、图5(c)可知，当弹道的初始状态偏离最优初始状态时，弹道轨迹均会偏离最优弹道轨迹，相应初始状态的目标函数值都低于最优初始状态的目标函数值。当初始速度偏离最优初始速度时，相应弹道轨迹偏离最优弹道的程度越来越大，且不能满足终端约束条件，对弹道性能影响最大。当初始速度倾角偏离最优初始速度倾角时，弹道轨迹偏离最优弹道的程度最低，首跳高度下降在几十米的量级。当初始高度偏离最优初始高度时，弹道轨迹偏离最优弹道的程度介于第六组和第五组之间，其首跳高度下降在几百米的量级。

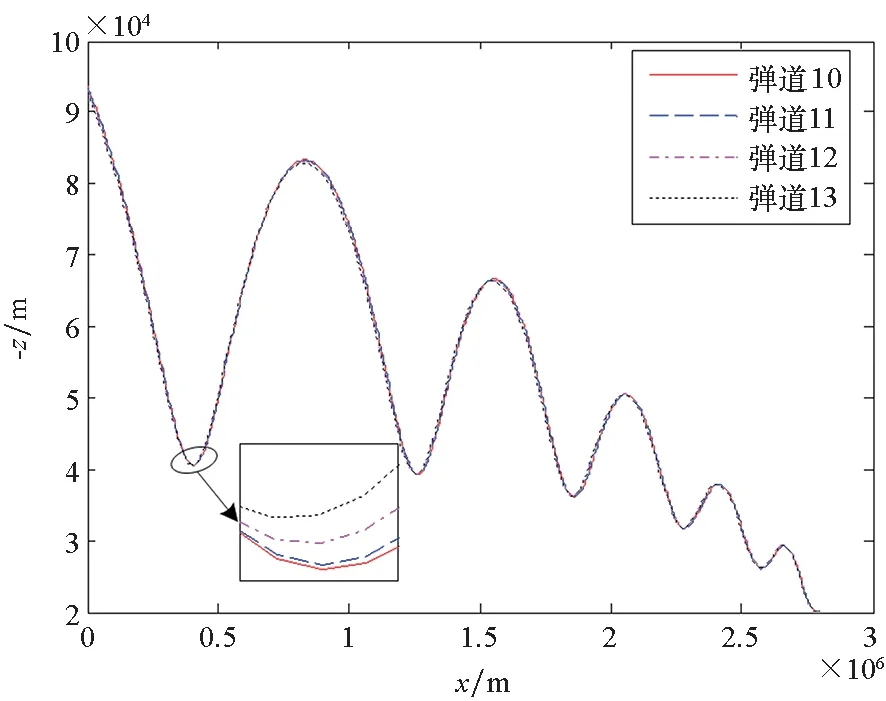
(a) 弹道10和第四组弹道的弹道轨迹仿真图

3.4.3 纵向加速度分析

图6是两组对比弹道和弹道10的纵向加速度曲线，因为第五组的三个弹道不满足终端约束条件，所以主要对第四组和第六组弹道的纵向加速度进行分析。从图6(a)中可以看出，当初始高度偏离最优初始高度时，纵向加速度曲线会偏离最优初始状态对应弹道的纵向加速度曲线。在飞行结束之前，弹道11、弹道12、弹道13均能完成最后一次纵向加速度符号翻转，所以弹道11、弹道12和弹道13的纵向机动变轨次数与弹道10相同。从图6(b)中可以看出，当初始速度倾角偏离最优初始速度倾角时，纵向加速度曲线会偏离最优初始状态对应弹道的纵向加速度曲线。在飞行结束之前，弹道17、弹道18、弹道19均未能完成最后一次纵向加速度符号翻转，所以弹道17、弹道18和弹道19的纵向机动变轨次数少于弹道10的纵向机动变轨次数。

(a) 弹道10和第四组弹道的纵向加速度

4 结论

针对临近空间高超声速滑翔飞行器滑翔段初始状态影响其弹道特性的规律问题，在平衡滑翔条件下，从理论上证明了纵向平衡滑翔弹道滑翔段初始状态的唯一性。由敏感性分析可知，当初始速度偏离平衡滑翔初始速度真值时，随着飞行过程的进行，其弹道逐渐发散，对弹道特性的影响最大；当初始速度倾角偏离平衡滑翔初始速度倾角真值时，其弹道轨迹、状态变量均趋向于收敛到平衡滑翔的弹道轨迹和状态变量，对弹道特性的影响最小。在跳跃滑翔条件下，利用粒子群算法求解了弹道性能最优时的滑翔段初始状态。由敏感性分析可知，当初始速度偏离跳跃滑翔最优初始速度时，其弹道不满足约束条件，相应弹道初始状态的目标函数值最低；当初始速度倾角偏离最优初始速度倾角时，从弹道轨迹的角度分析，其弹道轨迹最接近最优的弹道轨迹。