基于粒子群算法的宽带真延时平面阵列方向图综合*

丛雯珊，余 岚，杜鹏飞，罗 雄，杨海达

(空军预警学院 预警技术系， 湖北 武汉 430019)

为有效应对弹道导弹和高超声速等空天进攻武器的现实、潜在和未来威胁，迫切需要提高雷达的空间分辨能力。由阵列信号知识可知，雷达的空间分辨能力与阵列孔径成正比[1-2]，然而大型相控阵不仅造价昂贵，而且馈电网络的复杂度较高[3]。采用大阵元间距稀疏阵列天线虽然可有效规避上述问题，但其阵列方向图会出现与主瓣性质相同的栅瓣，不仅会引起辐射能量的分散，还会造成空间分辨模糊。

为了消除栅瓣对雷达性能的影响，获得尽量低的副瓣电平，国内外学者针对大阵元间距稀疏阵列天线方向图综合问题展开了大量的研究，提出了多种解决方法[4-10]。根据抑制栅瓣的原理不同，这些方法可以分为两类：其一是利用遗传算法[4-5]和粒子群算法[6-7]等智能优化算法优化阵列结构，破坏其相位的周期性，从而实现对栅瓣的抑制；其二是利用在真延时条件下，阵列方向图主瓣指向与信号频率无关，而栅瓣指向随信号频率变化的特点，通过发射宽带信号来抑制阵列方向图的栅瓣[8-10]。虽然上述两类方法都能抑制阵列方向图的栅瓣，但都存在一定的不足：第一类方法不仅随着阵元个数的增大其运算量会明显增大，而且随着阵元间距的增大其栅瓣抑制性能会下降；第二类方法对栅瓣的抑制性能与信号带宽有关，只有相对信号带宽达到100%才能有效抑制栅瓣[8]。同时，目前采用第二类方法抑制阵列方向图栅瓣的文章多数均是针对线阵的，针对平面阵列的还没有报道。

本文研究了一种基于粒子群优化算法的宽带真延时(WideBand real time delay based on Particle Swarm Optimization algorithm, WB+PSO)平面阵列方向图综合方法。这种方法在利用宽带真延时抑制栅瓣的基础上，采用粒子群优化算法来确定平面阵列中阵元的位置，从而实现对平面阵列方向图栅瓣的进一步抑制。通过对8×8的矩形平面阵进行仿真，验证该方法对大阵元间距平面阵列方向图栅瓣抑制的有效性。相比于宽带(WideBand, WB)方法，该方法在小信号带宽下也可有效抑制平面阵列方向图的栅瓣，其对栅瓣抑制性能受信号带宽影响较小。

1 基本理论与方法

1.1 平面阵宽带能量方向图

考虑由N×M个阵元组成的平面阵列，其空间几何关系如图1所示。X轴上有M个间距为d的均匀线阵，Y轴上有N个间距为d的均匀线阵，另假设宽带信号入射的方位角为θ，俯仰角为φ，其中方位角为信号入射在XY面上的投影与X轴之间的夹角。以阵列左上角的阵元为参考阵元，并设该阵元的坐标为(0,0)，则信号入射到第p(p=1,2,…,MN)个阵元与信号入射到参考阵元之间的时延差为：

图1 平面阵列空间几何关系Fig.1 Space geometrical relationship of planar array

(1)

式中：c=3×108m/s为光速，(xp,yp)为第p个阵元的坐标。假设各阵元为各向同性阵元，且接收特性相同，则各阵元接收的信号经过光延时网络后求和得[10]：

(2)

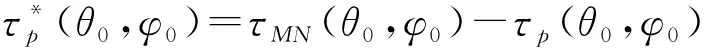
sin[kπ(χm-χn)(T-|χm-χn|)]

(3)

其中：χp=τp(θ,φ)-τp(θ0,φ0)为信号入射方向为(θ,φ)时与信号入射方向为(θ0,φ0)时相比，信号入射到第p个阵元与参考阵元时延差的差；f0、k和T分别为线性调频信号的中心频率、调频率和时宽。

1.2 WB+PSO平面阵方向图综合方法

粒子群算法又称PSO算法，是优化算法中一种以适应度函数作为导向的随机搜索算法，因其理论简单、参数少、易于编程实现及能同时对多维问题和非线性优化问题具有较强的搜索能力，已在阵列方向图综合、模式识别和信息处理等多个领域得到广泛应用。在阵列方向图综合方面，粒子群算法中的粒子通过式(4)来更新自己的速度和位置：

(4)

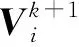
(5)

(6)

适应度函数是用来评价粒子群优化算法每次迭代后粒子优劣的，本文以抑制大阵元间距平面阵列方向图的栅瓣为优化目标，依据阵列能量方向图的归一化最高副瓣电平(Normalized Highest Sideband Level, NHSL)构造适应度函数，其定义式为：

(7)

式中，S为阵列方向图的副瓣区域。为有效抑制大阵元间距平面阵列方向图的栅瓣，获得高主副瓣比的阵列方向图，则目标函数为：

f(Xix,Xiy)=min(NHSLi)

(8)

根据上述理论分析及粒子群优化算法的步骤可知，本文提出的基于粒子群优化算法的宽带真延时阵列方向图综合方法的流程如图2所示。

图2 基于粒子群优化算法的宽带真延时阵列方向图综合方法的流程图Fig.2 Flow chart of the planar array pattern synthesis method of wideband real time delay based on particle swarm optimization algorithm

2 仿真实验

2.1 栅瓣抑制性能分析

仿真实验中平面阵列采用水平放置的8×8的平面阵，相邻阵元间的平均间距为3倍信号波长(信号中心频率所对应的波长)，相邻阵元间的最小间距为半个波长(即q=2)，控制光真延时网络的延时时间使阵列方向图的主瓣指向为(90°,0°)，粒子群个数为20，最大迭代次数为500，惯性权重系数为0，学习因子c1和c2均为2，结束条件为连续30次迭代NHSL的变化小于0.01或者迭代次数完成。当线性调频信号的中心频率、带宽和时宽分别为10 GHz、5 GHz和10 ns时，用本文方法得到平面阵各阵元的位置坐标(以半波长数为计量单位)如表1所示。图3(a)和图4(a)分别为此阵列本文方法和常规波束形成(Conventional BeamForming, CBF)算法得到的阵列方向图，图5(a)为该平面阵对应的均匀平面阵采用WB方法得到的阵列方向图，图3(b)、图4(b)和图5(b)分别为上述二维阵列方向图对应的水平投影。

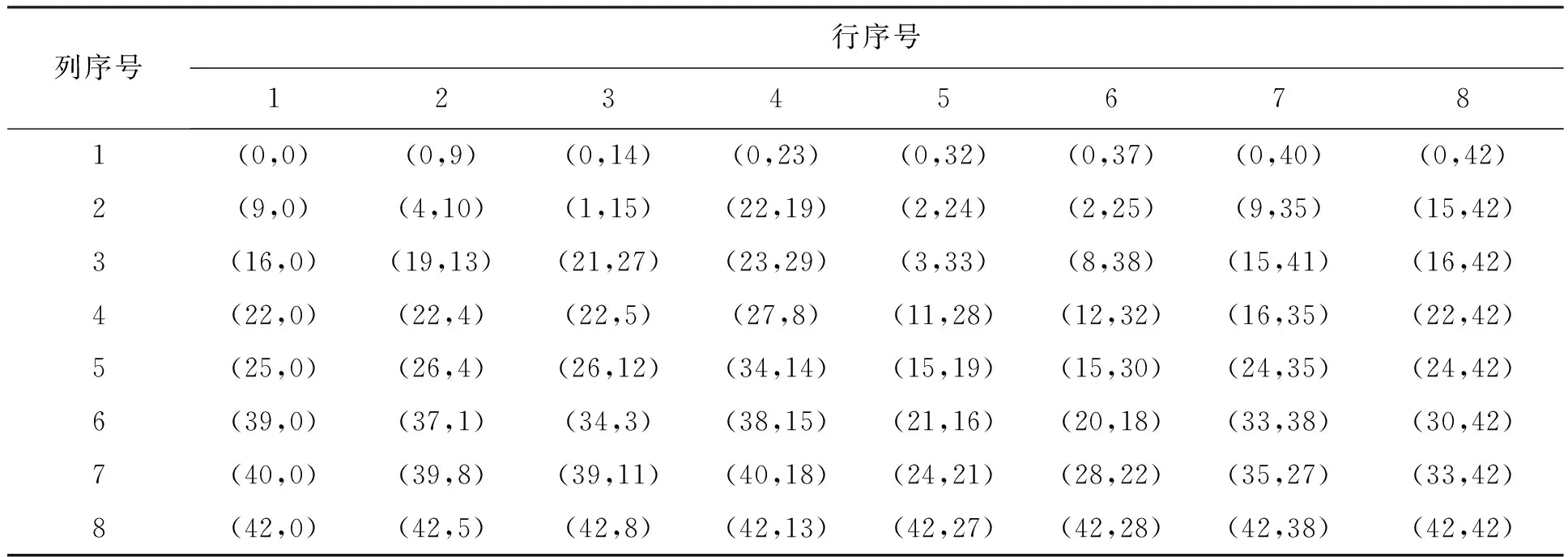
表1 平面阵各阵元的位置坐标

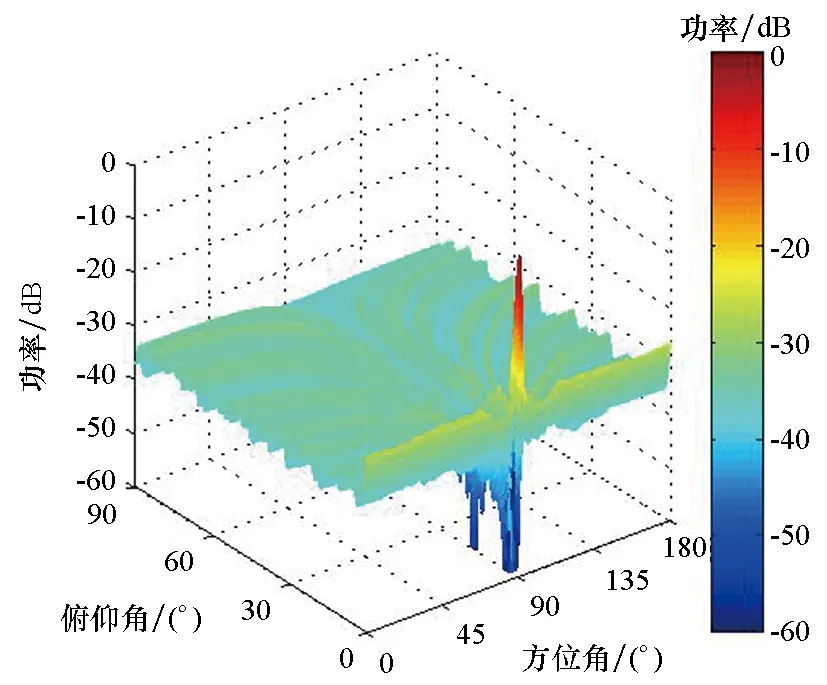
(a) 二维方向图

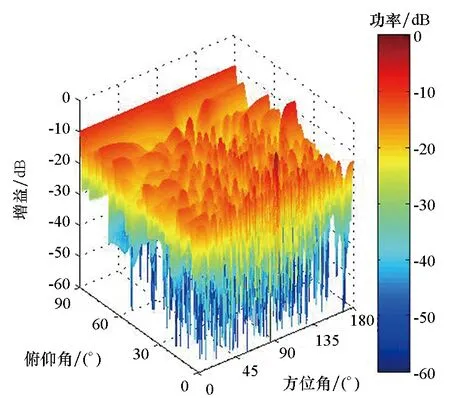
(a) 二维方向图

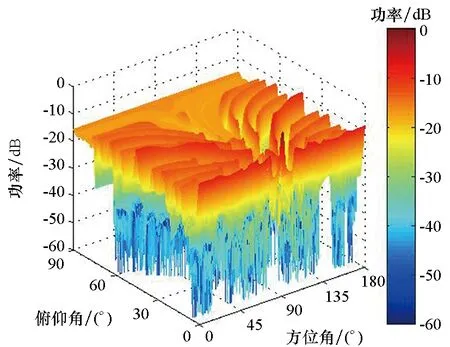
(a) 二维方向图

由图3～5可知，本文所提WB+PSO方法、CBF方法和WB方法得到的阵列方向图的NHSL分别为-13.11 dB、-7.55 dB和-8.61 dB。由此可知，相比于单独采用粒子群优化算法优化阵列结构和WB方法，WB+PSO方法对大阵元间距平面阵列方向图栅瓣的抑制性能更优，其对阵列方向图栅瓣的抑制性能分别改善了5.56 dB和4.50 dB。

2.2 对栅瓣抑制性能与信号带宽之间的关系

设置线性调频信号带宽的变化范围为1 Hz～18 GHz，步长为0.5 GHz，其余仿真条件与2.1节相同。CBF方法、WB方法和WB+PSO方法得到的阵列方向图的NHSL随信号带宽的变化关系如图6所示。

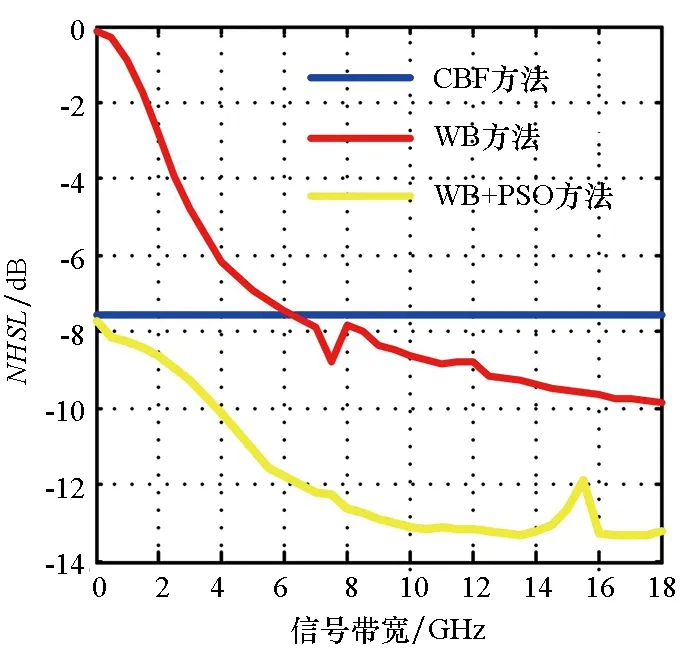
图6 NHSL随信号带宽的变化情况Fig.6 NHSL against signal bandwidth

由图6可知，WB方法和WB+PSO方法得到的阵列方向图的NHSL均随着信号带宽的增大而减小，但相比于WB方法，WB+PSO方法在小信号带宽下仍能实现对阵列方向图栅瓣的抑制，且WB+PSO方法对平面阵列方向图栅瓣的抑制性能受信号带宽的影响较小。

3 结论

本文研究了基于粒子群算法的宽带真延时平面阵列方向图综合方法，首先推导了基于宽带真延时的平面阵列能量方向图的基本模型，随后介绍了基于粒子群算法的宽带真延时平面阵列方向图综合方法的基本原理，最后进行了相应的仿真实验。仿真实验结果表明：相比于单独采用粒子群优化算法优化阵列结构的方法和WB方法，本文所提方法可更加有效抑制平面阵列方向图的栅瓣，提高阵列方向图主副瓣比；且相比于WB方法，本文方法在信号带宽较小时，也可抑制平面阵列方向图的栅瓣。因此，本文提出的方法为抑制雷达阵列方向图栅瓣提供了新的思路。