TDS-OFDM雷达通信共享信号波形设计*
2020-10-28左家骏杨瑞娟罗少华李晓柏
左家骏,杨瑞娟,罗少华,李晓柏
(空军预警学院 预警情报系, 湖北 武汉 430019)
雷达通信一体化共享信号(RadCom)技术,使用一种信号同时实现雷达与通信两种功能,不但能够有效降低平台的负重、能耗以及电磁干扰等,而且能大大提高对能量与频谱资源的利用率,近年来受到了军事与民用领域的广泛关注[1]。
正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)本身是在通信系统中广泛使用的一种多载波数据传输技术,由于其可调参数多、波形设计灵活,也逐渐应用于雷达领域,因此成为一种合适的共享信号体制。与通信系统类似,雷达一体化系统通常使用多个OFDM符号组成的脉冲信号实现大容量数据传输[2-4]。为了对抗多径引起的符号间干扰,在OFDM符号之间需要设置一定长度的保护间隔,一般使用循环前缀(Cyclic Prefix, CP)进行填充。
CP的存在提高了信号的正交性,减少了载波间干扰。但是将CP-OFDM信号用于雷达通信一体化系统时,CP作为OFDM数据块后一段的复制,在自相关运算中,不可避免地会产生较高的峰值副瓣电平(Peak Side lobe Level, PSL)[5],并且CP占比越大,副瓣电平越高。另外,为了进行通信同步与信道估计,CP-OFDM共享信号还必须使用导频,而无论是梳状、块状还是梅花状导频,都会产生一定的导频副瓣[6]。在雷达目标检测中,这些副瓣容易形成假目标,在多目标环境下还将产生严重的遮蔽问题,严重制约了OFDM雷达通信一体化信号在实际中的应用。
针对这一问题,文献[7-8]提出了将参考信号的CP与导频置零,然后再与回波信号相关的做法。该方法能够有效去除CP及导频副瓣,但损失了信号能量,使脉压增益下降,大大降低了雷达探测性能。针对CP-OFDM存在的难以解决的CP及导频副瓣问题,本文提出了一种新的基于时域同步OFDM(Time Domain Synchronization, OFDM, TDS-OFDM)的共享信号形式。TDS-OFDM信号用训练序列取代CP,填充到保护间隔中,该序列同时也作为通信同步与信道估计的训练序列。因此,TDS-OFDM信号不再需要设置循环前缀与导频,从而避免了CP及导频副瓣的问题。
TDS-OFDM是数字电视地面广播(Digital Terrestrial Television Broadcasting, DTTB)标准中的关键技术,DTTB标准在中国、古巴、柬埔寨等国已得到成功应用,在通信方面已发展得较为成熟[9],因此本文主要探讨TDS-OFDM共享信号在雷达方面的性能。首先推导TDS-OFDM共享信号的模糊函数,在此基础上提出兼顾雷达与通信性能的训练序列设计准则,建立优化的数学模型,然后采用序列二次优化(Sequence Quadratic Program, SQP)算法,求解满足条件的训练序列。
1 信号模型
设计的信号采用脉冲体制,如图1所示,每个TDS-OFDM共享信号的脉冲由N个OFDM符号组成,每个OFDM符号包含时长为Tg的保护间隔和时长为Tb的数据段,保护间隔则由一段训练序列替代CP填充。将一个TDS-OFDM共享信号脉冲的包络表示为两部分之和

图1 TDS-OFDM共享信号结构示意图Fig.1 Structure diagram of TDS-OFDM RadCom signals
s(t)=A1s1(t)+A2s2(t)
(1)

(2)
(3)
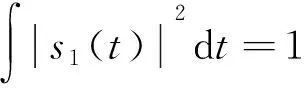

2 模糊函数推导
当雷达采用匹配滤波接收时,模糊函数反映了信号经过匹配滤波器后的时延-多普勒特征,是研究雷达信号以及波形设计的重要工具,本节详细推导了TDS-OFDM雷达通信共享信号的模糊函数。
2.1 TDS-OFDM共享信号的模糊函数
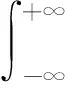
对于一般的点目标,可用如下的窄带模糊函数进行分析。
(4)
式中,τ表示时延,ξ表示多普勒频移。将式(1)代入式(4)可得TDS-OFDM共享信号的模糊函数χs(τ,ξ)为

A1A2χ1,2(τ,ξ)+A1A2χ2,1(τ,ξ)
(5)

(6)
实际上,增大OFDM脉冲的时宽带宽积或者在脉冲压缩后采用相参积累,都能有效减小χs(τ,ξ)的方差[10],因此近似有
χs(τ,ξ)≈ε[χs(τ,ξ)]
(7)
结合式(6)、式(7),因此χs(τ,ξ)就等于χ1,1(τ,ξ)与ε[χ2,2(τ,ξ)]的关于能量比值的加权和。其中OFDM数据段的模糊函数的期望ε[χ2,2(τ,ξ)]已由文献[5]给出,可表示为
ε[χ2,2(τ,ξ)]=(Tb-|τ|)sinc[ξ(Tb-|τ|)]·
-Tb<τ≤Tb
(8)
以下重点推导训练序列串的模糊函数。
2.2 训练序列串的模糊函数
将式(2)代入式(4)可得
(9)
求解式(9)中的积分项,最终可得训练序列串的模糊函数为
(T1-|ΔkT1+ΔnT2-τ|)ejπξ[(k+k′+1)T1+(n+n′)T2+τ]·
sinc[ξ(T1-|ΔkT1+ΔnT2-τ|)]},
|ΔkT1+ΔnT2-τ|≤T1
(10)
式中,Δk=k-k′,Δn=n-n′。 Δk、Δn的取值决定了时延τ的范围。 令τ=0,可知Δk=0、Δn=0,可得训练序列串模糊函数的零时延切片为
(11)
训练序列具有恒模的性质,因此式(11)表明,训练序列串的速度自相关函数与训练序列的取值无关,不同的训练序列都具有相同的多普勒容限,因而在训练序列串设计时,不需要考虑对多普勒容限的影响。 另外,在式(10)中取τ=ΔkT1+ΔnT2,令ξ=0,可得训练序列串的距离自相关函数为
(12)
从式(12)可以看出,当Δn=0,即在-T2<τ
将式(8)、式(10)代入式(6),可得到TDS-OFDM共享信号模糊函数的期望,其具体的数学表达式不再赘述。在N=8、M=128、K=32的条件下,对OFDM数据段模糊函数期望、训练序列串模糊函数以及TDS-OFDM共享信号模糊函数期望进行了仿真,分别如图2、图3、图4所示,图中数值均归一化。由图可以看到,TDS-OFDM共享信号的模糊函数在时延轴上表现出间隔的栅瓣,并且主要是由训练序列串引起,因此需要对训练序列进行优化设计。在归一化多普勒频移等于0.25处,速度自相关函数取值约为0.9,反映了其多普勒容限与常规OFDM共享信号一致[11]。

图2 OFDM数据段模糊函数期望Fig.2 Ambiguity function expectation of OFDM data segment

图3 训练序列串模糊函数Fig.3 Ambiguity function of training sequence string

图4 TDS-OFDM共享信号模糊函数期望Fig.4 Ambiguity function expectation of TDS-OFDM RadCom signals
3 训练序列优化设计
雷达距离副瓣是影响雷达目标检测的一个重要因素,在多目标环境中,副瓣电平过高使得强信号的副瓣会掩盖弱信号主峰。因此,需要对训练序列进行优化设计,抑制TDS-OFDM共享信号的距离副瓣。根据前面的推导,将TDS-OFDM信号自相关序列的期望的PSL作为优化的其中一个目标函数:
(13)
式中,ε[χs(k)]表示TDS-OFDM共享信号的自相关序列的期望,Nχ表示信号的最大采样点数。为了降低一个符号时延范围内的副瓣,自相关运算中使用了汉明窗加权处理。
另外,为了实现通信同步以及信道估计,还需要训练序列本身具有较好的自相关性。用rn,n(k)表示第n个训练序列的非周期自相关函数
(14)
将N个训练序列的最大峰值副瓣作为另外一个目标函数
(15)
因此,训练序列的设计准则是要同时降低PSLTS与PSL0。应用约束非线性规划,建立如下的数学模型:
mins
(16)
式中:s既是目标函数,也是优化的辅助变量,通过最小化s,该模型同时降低PSLTS与PSL0;μ>0表示加权系数,用于调整两个优化目标之间的比重,二者的关系是
PSLTS=μPSL0
决策变量φn,k的取值范围为[0,2π),因此得到的训练序列的相位是连续的,具有比离散相位更高的自由度。
令优化变量为x=[φ0,…,φK-1,s],式(16)即可转化为标准优化模型。对于这个非线性优化问题,采用SQP算法求解。SQP算法的核心思想是:在每一次迭代中,先使用拟牛顿法逼近由目标函数和约束函数增广而成的拉格朗日函数的海森矩阵;再通过海森矩阵产生一个二次规划子问题,并求解得到变量的搜索方向;然后通过线性搜索确定步长;最后用搜索方向和步长来更新当前的变量。在SQP求解过程中,需要设定变量的初始值,由于没有先验信息,实验中采用[0,2π)中随机生成的相位作为训练序列初始值,s的初始值设为1。
4 仿真实验与分析
采用MATLAB优化工具包中的fmincon函数对式(16)进行求解,fmincon函数调用了SQP算法。在实验参数设计中,以IEEE802.11a协议中OFDM信号帧结构为蓝本,确定了OFDM共享信号的载波频率、带宽、保护间隔、符号长度等参数,同时考虑到S波段雷达的要求,确定了脉冲宽度与OFDM符号数。相关信号参数如表1所示,SQP最大迭代次数为100。
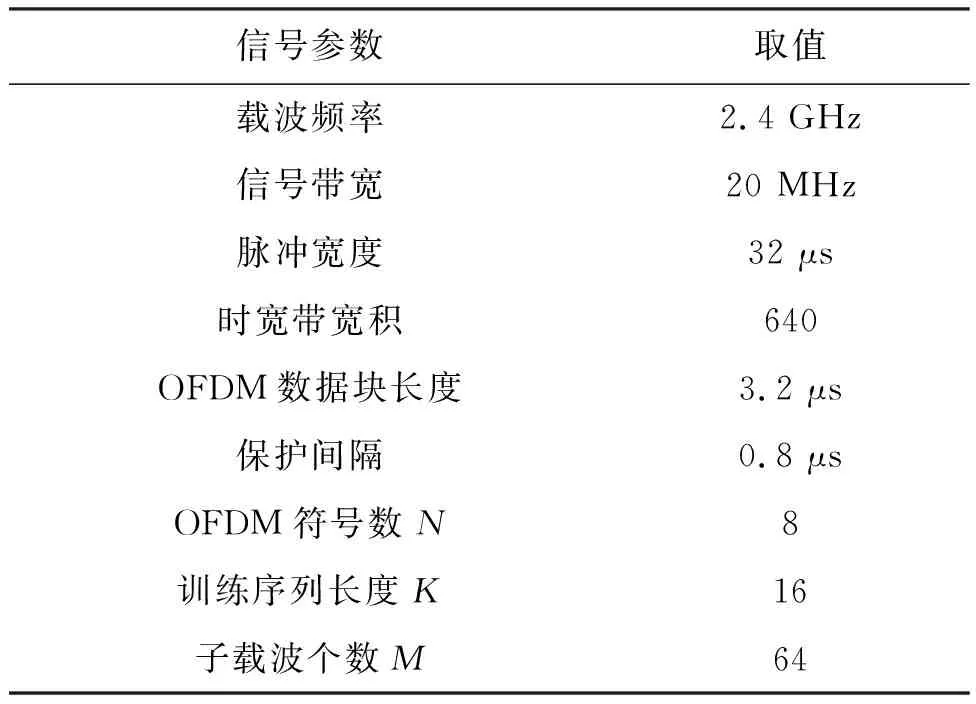
表1 OFDM信号参数
4.1 训练序列设计
令权重μ=6.5,在一次随机实验中,得到了以下仿真结果。表2给出了所设计的训练序列串的相位信息。图5所示为训练序列的自相关函数,8个训练序列的自相关峰值副瓣均为-18.78 dB,表现出十分良好的自相关性,可使信号在通信方面具有较好的同步与信道估计性能。

表2 所设计的训练序列串

图5 训练序列的自相关函数Fig.5 Autocorrelation function of training sequence
TDS-OFDM共享信号自相关函数的期望如图6所示,PSL0达到了-34.78 dB。因此在平均意义上,所设计的信号具有较好的对微弱目标检测能力。

图6 TDS-OFDM共享信号的距离自相关函数期望Fig.6 Expectation of autocorrelation function of TDS-OFDM RadCom signals
4.2 TDS-OFDM与CP-OFDM性能比较
在表1所示的信号参数条件下,对TDS-OFDM共享信号与CP-OFDM共享信号的模糊函数进行了仿真,其中TDS-OFDM共享信号采用的是4.1节所设计的训练序列。
图7所示为TDS-OFDM共享信号的模糊函数,其形状为理想的图钉型,自相关副瓣电平较低,受到通信数据的影响,自相关副瓣存在一定的随机波动。图8所示为CP-OFDM共享信号的模糊函数,可以看到在时延轴上,存在着两组对称的伪峰,这是由CP与导频所引起的副瓣,并且副瓣电平较高,将会严重影响雷达的目标检测性能。通过对比可以看到,经过优化设计的TDS-OFDM共享信号很好地解决了CP副瓣与导频副瓣问题,极大地改善了信号自相关性能。

图7 TDS-OFDM共享信号模糊函数Fig.7 Ambiguity function of TDS-OFDM RadCom signals
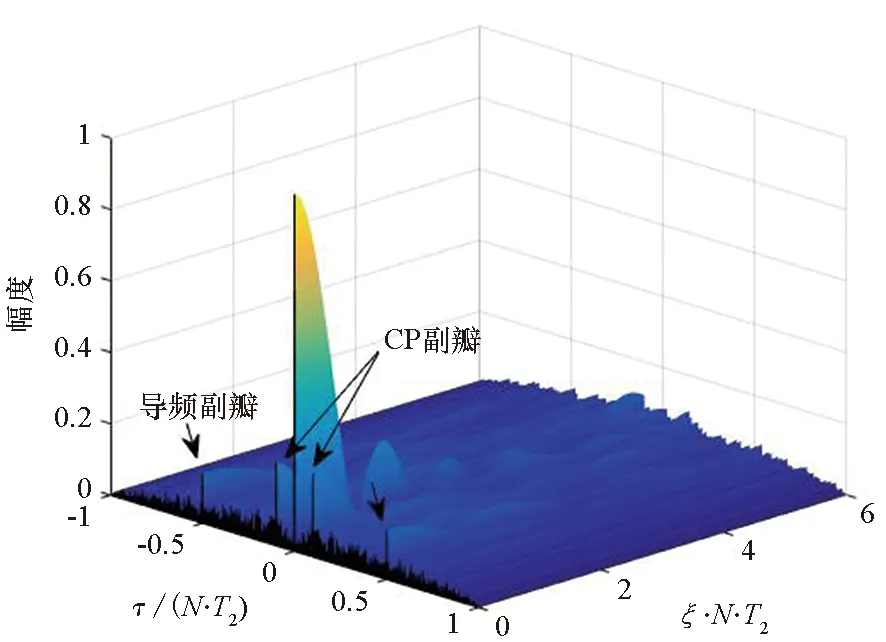
图8 CP-OFDM共享信号模糊函数Fig.8 Ambiguity function of CP-OFDM signal
另外,可采用相参积累技术降低单脉冲信号自相关函数的波动,进一步降低TDS-OFDM共享信号的副瓣。为了说明这个问题,对经过P个脉冲相参积累后的TDS-OFDM共享信号距离自相关函数进行了仿真,P分别为1、4、16、64。
图9给出了TDS-OFDM共享信号的距离自相关函数仿真结果。可以看到,自相关函数中存在类似“噪声”的基底,这是由通信数据引起的副瓣随机波动。受其影响,单脉冲的PSL仅有-20 dB左右,而随着积累的脉冲数增加,PSL逐渐降低,当P=64时,PSL约为-33 dB,已十分接近PSL0。该仿真表明,增加相参积累脉冲数,能够有效降低通信数据随机性的影响,使自相关函数趋近于期望值。由于现代雷达普遍采用相参积累技术,因此,优化信号自相关函数期望的方法是有效的。
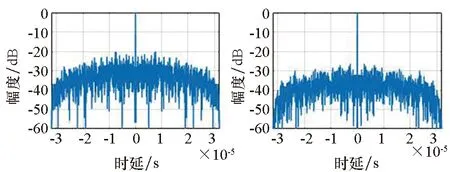
(a) P=1 (b) P=4
4.3 加权系数的影响分析
在不同的权重μ取值条件下,对SQP算法进行了仿真。图10给出了所设计训练序列的PSLTS与PSL0随权重μ的变化曲线。从图中可看出,在双对数坐标系下,随着权重μ增大,PSLTS近似线性升高,而PSL0近似线性降低。二者的差值,即为权重μ的取值。

图10 优化目标与加权系数关系曲线Fig.10 Optimization objective versus weight
另外,PSL0降低的速度比PSLTS升高的速度快。这表明,适当牺牲PSLTS,可以使PSL0获得较大改善。但没有必要追求极低的PSL0,一方面是因为μ过大容易导致算法性能下降,另一方面是信号PSL还受到前述“噪声”的影响。因此要根据实际情况,综合考虑雷达、通信对训练序列性能的要求,合理确定加权系数μ的取值。
5 结论
为了解决传统CP-OFDM共享信号存在CP副瓣与导频副瓣的问题,本文提出了一种基于TDS-OFDM的共享信号方案。通过训练序列的优化设计,有效降低了TDS-OFDM信号的距离峰值副瓣,同时也保持了训练序列自身的自相关性,从而兼顾雷达和通信性能。但不可否认的是,TDS-OFDM信号在通信端的处理更加复杂,尤其是在信道估计时需要去除训练序列与OFDM数据块的相互影响,增加了计算量。但综合考虑,相比于CP-OFDM在雷达目标检测中存在的问题,TDS-OFDM更加适合于雷达通信一体化系统。
