位移载荷下折叠式压电振子的疲劳分析

赵春明，龚立娇，周天烁，张 新，张鹏飞

(石河子大学 机械电气工程学院，新疆 石河子 832003)

0 引言

压电俘能器利用压电材料的正压电效应将振动能转换为电能，通过匹配能量采集电路，为负载提供电能。通常压电俘能器的结构简单且易发电，因而国内外专家已广泛研究[1-2]。本文提出的一种折叠式压电振子结构[3]由压电层、弹性层和粘结层组成。在实际应用中，压电振子的固有频率与环境的振动频率接近，使其机电转换性能得到充分利用。相应地，随着交变位移作用，折叠压电振子的各部分材料将会出现疲劳现象，直至结构产生破坏。由此可见，疲劳寿命将成为影响压电振子输出电能的一个重要因素[4-5]。

目前对压电振子振动发电性能的研究较多，而其中粘结层对压电结构性能的影响显著[6-7]。Jurk M等[8]给出了评估粘结层对压电式传感器质量影响的方法。Jin Congrui等[9]提出了粘结层的几何与材料特性对单晶压电振动悬臂梁结构的机电耦合的影响。Anil Can Turkmen等[10]设计了一种拔型压电能量采集装置，将其嵌入人的鞋跟中，通过人行走时自身体重作为谐波载荷作用在装置上。当质量为90 kg的人正常行走时，可产生的电能为1.43 mW，但未考虑装置的使用寿命。张淼等[11]通过给悬臂梁式压电振子施加位移激励，然后对压电层进行疲劳分析，但未考虑粘结层对压电振子的疲劳影响。在实际应用中，压电振子由于各层间边缘处的不连续及材料参数差异较大，而粘结层表面会出现复杂的应力分布，且在中间层的两端圆角位置会出现高度的应力集中，这影响了压电结构的使用寿命。

本文针对一种折叠式压电振子，对其粘结层进行理论分析，通过Ansys Workbench建立有限元模型；同时考虑在位移载荷下，分析粘结层厚度对折叠式压电振子的弹性层和压电层的应力影响；将静力分析结果传输到nCode DesignLife疲劳软件，对压电层进行疲劳寿命分析。

1 折叠式压电振子粘结层理论分析

折叠式压电振子由弹性折叠梁、压电片及粘结层组成，如图1(a)所示。弹性折叠梁的上、下表面粘贴压电陶瓷片，折叠梁的长、宽、高分别为L、W、H，弹性层的厚度为h2；压电片的长度、厚度分别为lp,h1(h3)；粘结层的厚度为ha。建立折叠式压电振子的局部坐标系如图1(b)所示。图中，x1(x3),x2分别为压电层、弹性层的横坐标，z1(z3),z2分别为压电层、弹性层的纵坐标，u1(u3),u2分别为压电层、弹性层的轴向位移，w1(w3),w2分别为压电层、弹性层的横向位移。

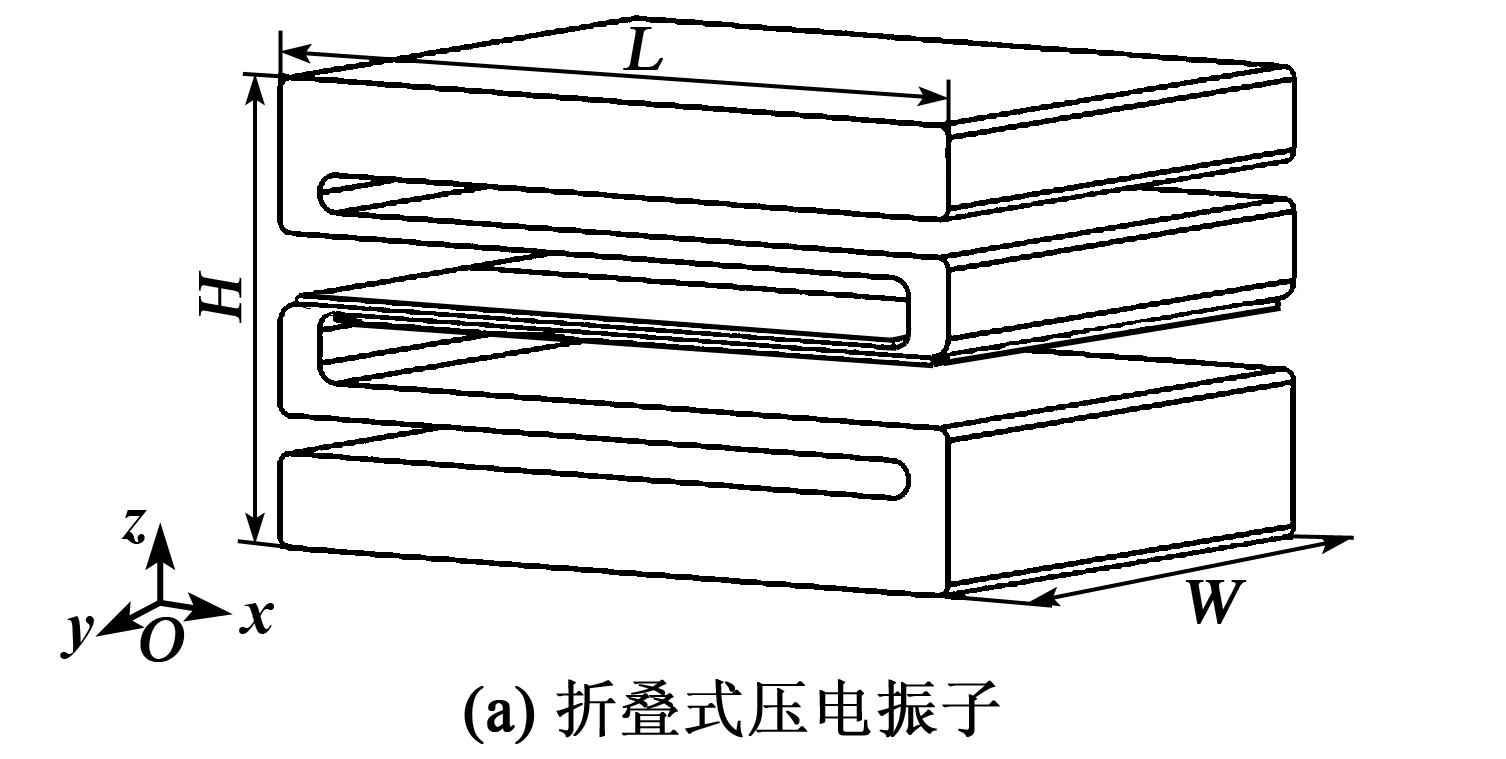
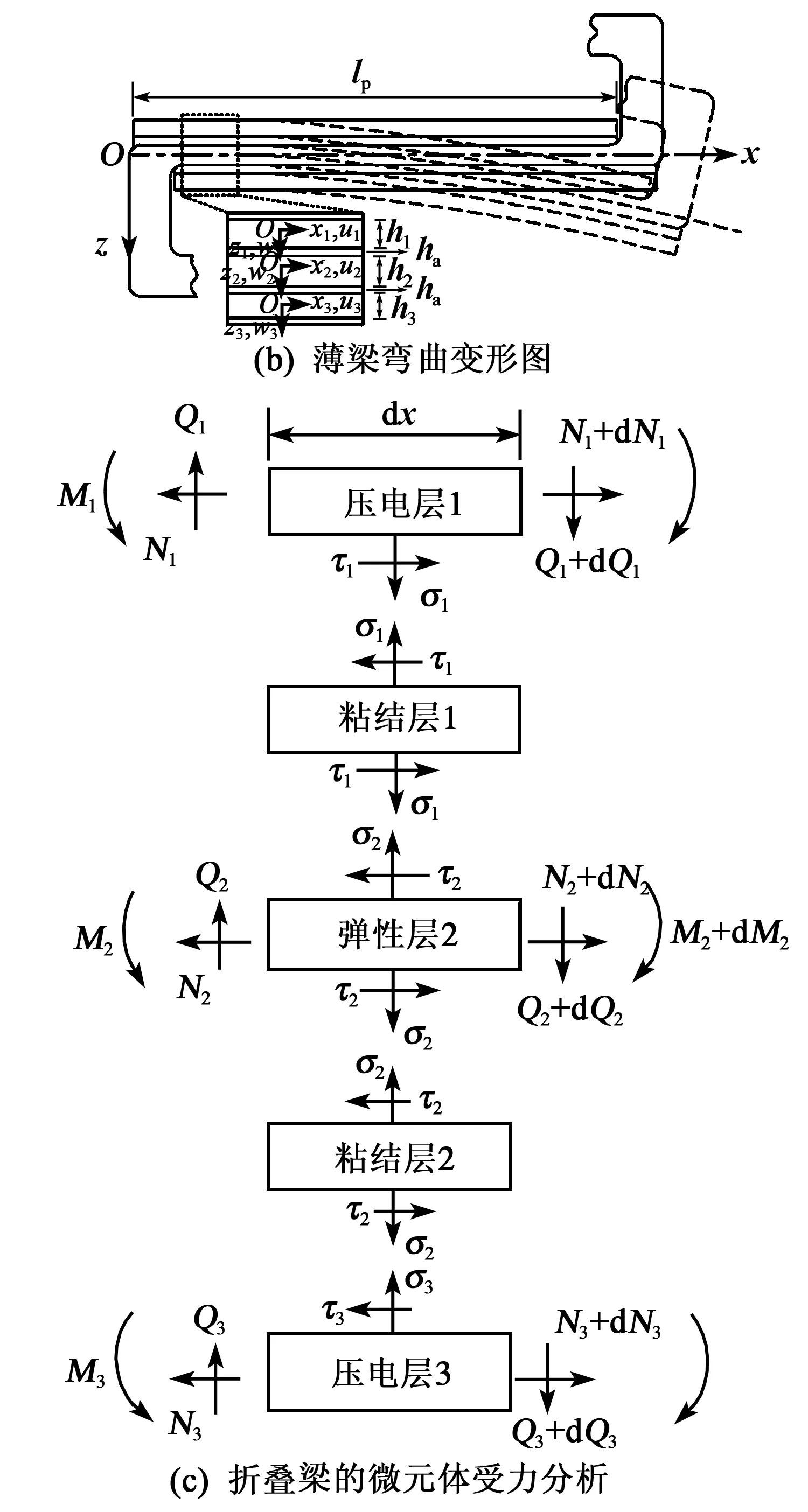
图1 折叠式压电振子结构

假设折叠式压电振子中层与层的材料参数与几何参数不同，而同一层的材料性能与厚度相同，各层材料为各向同性材料，则折叠梁各层中任一点的轴向位移Ui(xi,zi,t)及横向位移Wi(xi,zi,t)[12]分别为

(1)

Wi(xi,zi,t)=wi(x,t)

(2)

粘结层1、2的上、下表面轴向位移U′1、U″1、U′2、U″2分别为

(3)

(4)

(5)

(6)

粘结层1、2的剪应变分别为

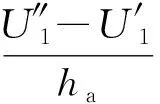
(7)

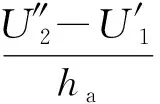
(8)

折叠梁的微元体受力分析如图1(c)所示。各层中存在轴力Ni、弯矩Mi和剪力Qi(i=1(3)，2表示压电层和弹性层)；τ1(2)，σ1(2)分别为粘结层1、2的切应力和剥离应力。

为便于分析计算，粘结层内的剪切应力、剥离应力沿其厚度方向保持不变，同时可忽略粘结层惯性力的影响。粘结层1的切应力：

(9)

剥离应力：

(10)

粘结层2的切应力：

(11)

剥离应力：

(12)

式中Ga,Ya分别为粘结层的剪切模量和弹性模量。

随着位移载荷作用在折叠压电振子上，中间层产生弯曲变形。为了防止折叠式压电振子在粘结层处剪切破坏，根据式(1)、(2)可推导出粘结层的剪应变、切应力及剥离应力。由式(7)、(9)、(10)可见，对于折叠式压电振子，随着粘结层厚度的减小，其剪切强度增大；而粘结层的切应力、剥离应力增大，则会产生折叠压电振子的疲劳破坏，减少使用寿命。因此，本文通过施加位移载荷，研究了粘结层厚度对折叠式压电振子的疲劳寿命影响。

2 折叠式压电振子的建模与静力分析

2.1 建模方法与过程

由图1所示的一种折叠式压电振子，本文选用Ansys Workbench软件建立有限元模型。在建模过程中，粘贴于中间薄梁上、下表面的4个压电陶瓷片，因同一层的变形区域相同，可等效粘贴为上、下两个压电片。

折叠梁结构尺寸：L=34 mm，W=27 mm，H=19.5 mm，h2=0.3 mm，lp=32 mm，h1=h3=0.22 mm。粘结层长为32 mm，ha=0.01～0.1 mm。构成折叠式压电振子的材料：弹性折叠梁选用304钢，压电材料选用P-51，粘结层选用胶体材料环氧树脂胶，具体参数如表1所示。

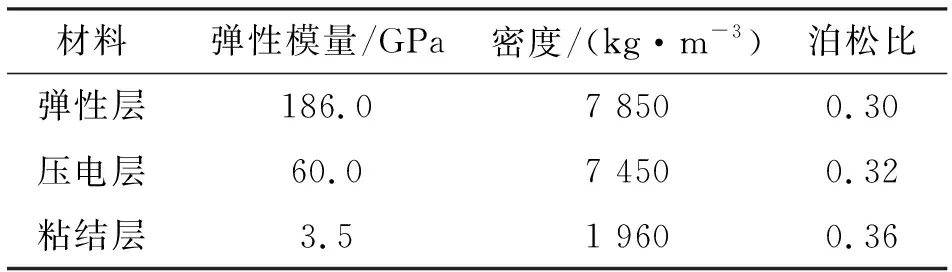
表1 折叠式压电振子参数

设置折叠式压电振子的材料属性，然后进行网格划分。弹性折叠梁与粘结层可采用四面体单元类型，压电层采用六面体单元类型。而在中间薄梁两端圆角的过渡位置，为避免应力奇异点，可采用局部网格优化。图2为折叠式压电振子的有限元模型。

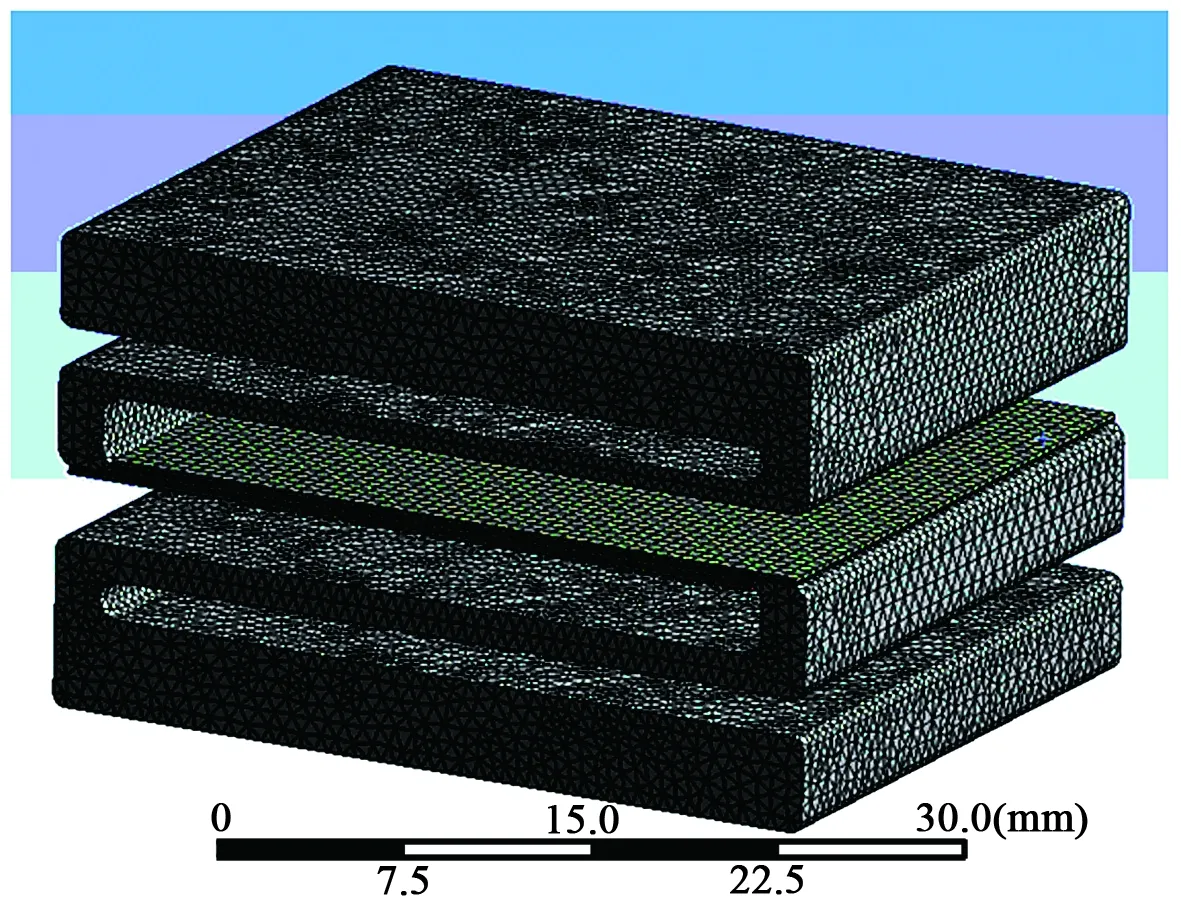
图2 折叠式压电振子有限元模型

2.2 折叠压电振子静力分析

网格划分后，对折叠式压电振子进行静力分析。假设粘结层在弹性层与压电层之间均匀分布，位移连续，且弹性层与压电层受力均匀。通常，粘结胶体材料的剪切强度数值越大，其粘接的强度越高。本文粘结层的性能参数取室温(25 ℃)，粘结强度(即拉伸极限强度)为31 MPa。

对折叠式压电振子的底面采取固定约束，其弹性层、压电层的应力分布对应以下3种工作模式：

1) 频率为85.5 Hz时，在折叠压电振子的最上层质量块的左侧面施加大小1 mm、方向竖直向下的位移载荷，分析得到等效应力分布云图，如图3(a)所示。

2) 频率为105.8 Hz时，对折叠压电振子的上表面施加大小为1 mm、方向竖直向下的位移载荷，分析得到等效应力分布云图，如图3(b)所示。

3) 频率为153.2 Hz时，对折叠压电振子最上层质量块的前、后面均施加大小为1 mm、方向竖直向下的位移载荷，分析得到等效应力分布云图，如图3(c)所示。

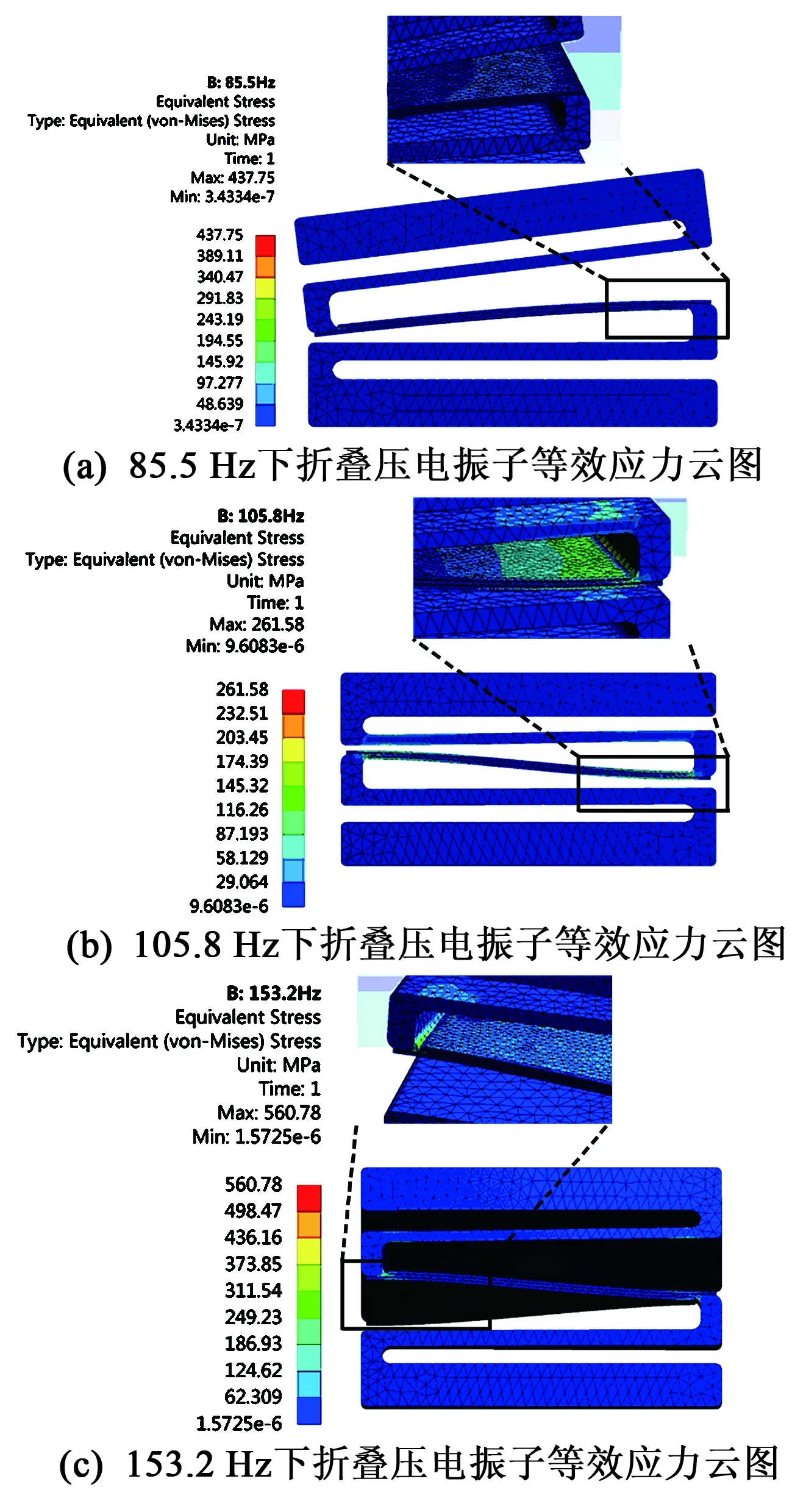
图3 折叠压电振子等效应力分布图

由图3可见，85.5 Hz时折叠压电振子薄梁部分发生左、右横向振动；105.8 Hz时薄梁部分发生上、下横向振动，是常见的工作模式，弹性层的应力分布集中在两端圆角的过渡位置，所处位置的应力值为203.45 MPa；153.2 Hz时薄梁部分发生扭转振动。通过分析折叠压电振子的应力变化，可得弹性层与压电层随粘结层厚度变化的应力曲线，如图4、5所示。

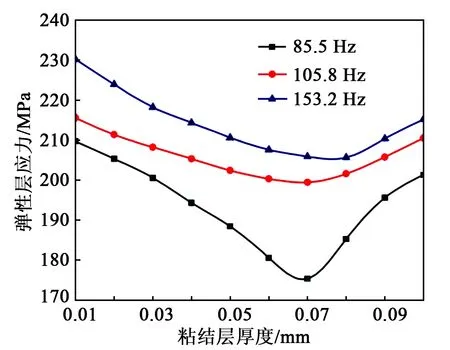
图4 弹性层应力随粘结层厚度变化曲线

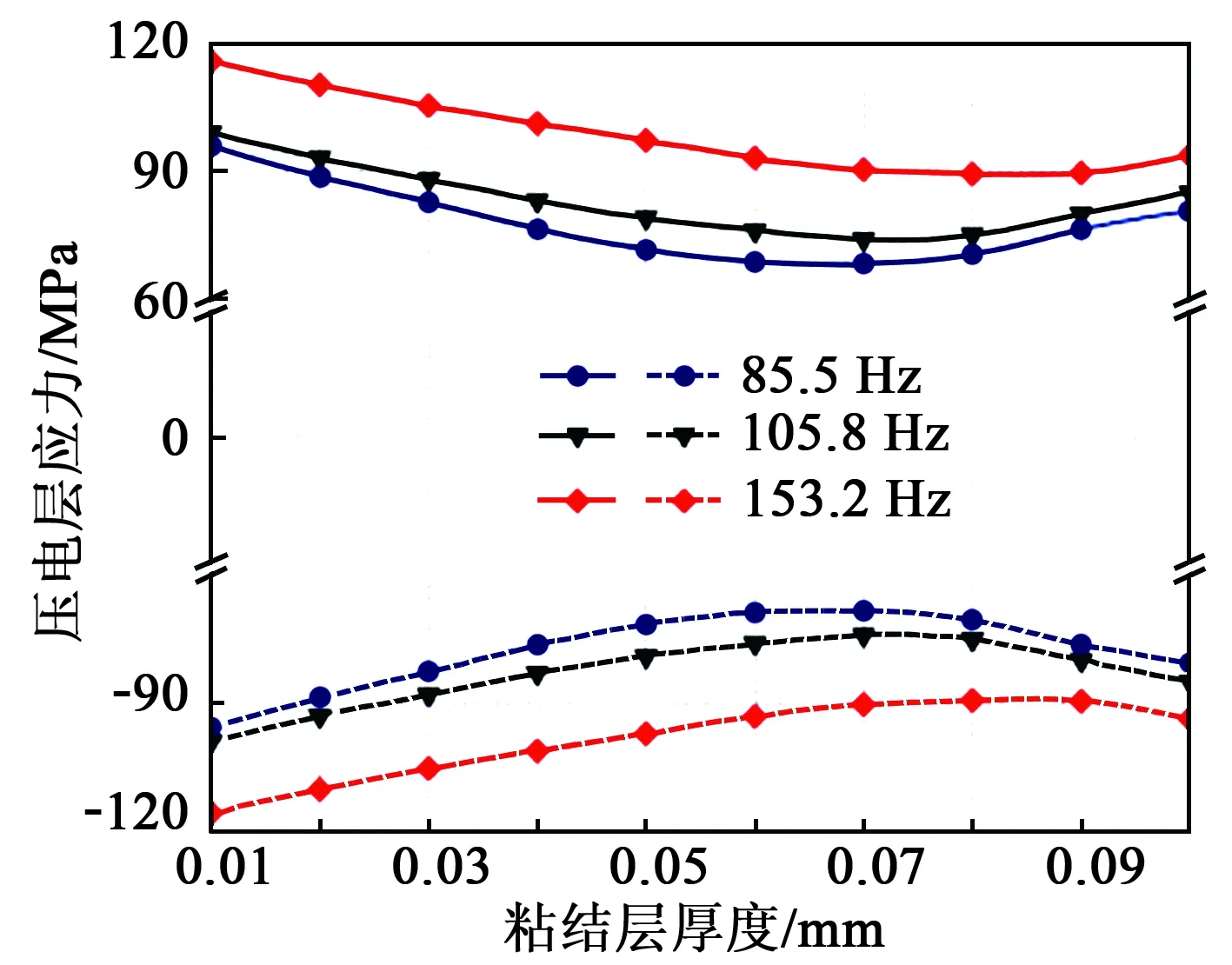
图5 压电层应力随粘结层厚度变化曲线

弹性层的屈服强度为205 MPa。由图4可见，弹性层分别在85.5 Hz、105.8 Hz，粘结层厚分别为0.03～0.10 mm及0.05～0.08 mm时，所受应力小于许用应力值，满足弹性层抵抗微量塑性变形的要求。其中，当粘结层厚为0.07 mm时，弹性层在不同频率下所受应力最小，当85.5 Hz时，弹性层应力值为175.34 MPa。

折叠压电振子在频率153.2 Hz的作用下，粘结层厚为0.07～0.08 mm。应力值接近弹性层的屈服强度，在长久的工作条件下，将使折叠压电振子永久失效，无法恢复强度要求。

本文研究的折叠式压电振子为中心对称结构。由图3可以看出，上下压电层的应力大小相等，方向相反。当薄梁部分发生弯曲变形时，沿其长度方向的上下压电层的应力表现为一侧拉应力，另一侧为压应力。由图5可以看出，折叠压电振子在不同的工作模式下，粘结层厚度为0.06～0.08 mm时，压电层的应力值最小。85.5 Hz时压电层所受应力值为68.34 MPa。

因此，折叠压电振子在不同的工作模式下，通过分析弹性层与压电层的应力变化可知，当粘结层厚为0.07～0.08 mm，应力变化最小。为保证折叠式压电振子能长时间工作，现对其进行疲劳寿命分析。

3 折叠式压电振子的疲劳分析

本文选用nCode DesignLife软件对折叠式压电振子进行疲劳寿命分析。疲劳是结构在应力或应变的反复作用下发生破坏的现象。疲劳寿命是指结构发生破坏时，循环载荷作用的次数或时间。

将其静力分析的结果传输到疲劳分析软件中，选用时间载荷的应力-寿命模块。弹性折叠梁的材料为304钢，其应力-寿命疲劳特性曲线可通过nCode材料库直接获取；而压电材料与粘结层在材料库中无对应的应力-寿命曲线，可通过压电材料的弹性模量(60 GPa)、拉伸极限强度(77 MPa)及粘结层的弹性模量(3.5 GPa)、拉伸极限强度(31 MPa)进行自定义，生成修正的应力-寿命曲线。

设置弹性层、压电层和粘结层结构材料参数。设置正弦位移载荷幅值为1 mm，作用时间为1 s。经过疲劳寿命计算，在3种工作模式下折叠式压电振子的寿命分布如图6所示。

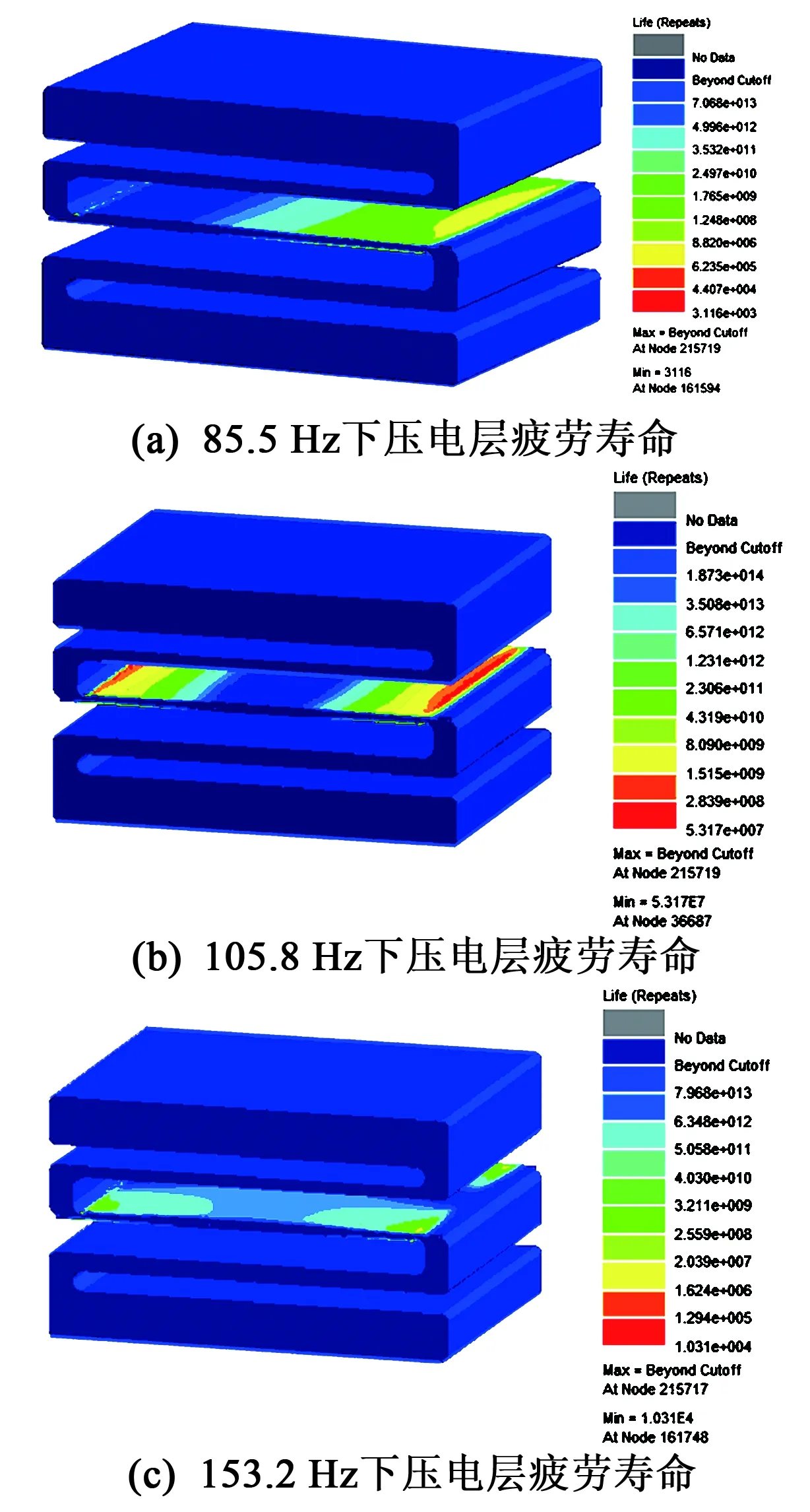
图6 折叠式压电振子压电层的疲劳寿命分布

由图6可见，折叠压电振子在振动过程中，结构的疲劳破坏发生在压电层。85.5 Hz下，结构发生左、右横向振动，位于薄梁端部的压电层的疲劳寿命次数为8.82×106。在常用的工作模式105.8 Hz时，薄梁部分发生上、下横向振动，压电层的破坏发生在中间薄梁圆角两端的过渡位置，疲劳寿命次数为5.317×107。153.2 Hz下，薄梁部分发生扭转振动，压电层的疲劳寿命次数为1.624×106。在3种工作模式下，通过分析折叠压电振子压电层的疲劳寿命，得到压电层随粘结层厚度变化的疲劳寿命曲线(见图7)。由图7可知，当粘结层厚度在0.07～0.08 mm时，压电层的疲劳寿命最高。在105.8 Hz时，其疲劳寿命次数可达107；而在85.5 Hz和153.2 Hz时，压电层的疲劳寿命次数为106。这是因为在位移载荷下，薄梁部分发生左、右横向振动和扭转振动时，压电层在薄梁部分两端圆角的过渡位置产生应力集中，使疲劳寿命减小1个数量级。

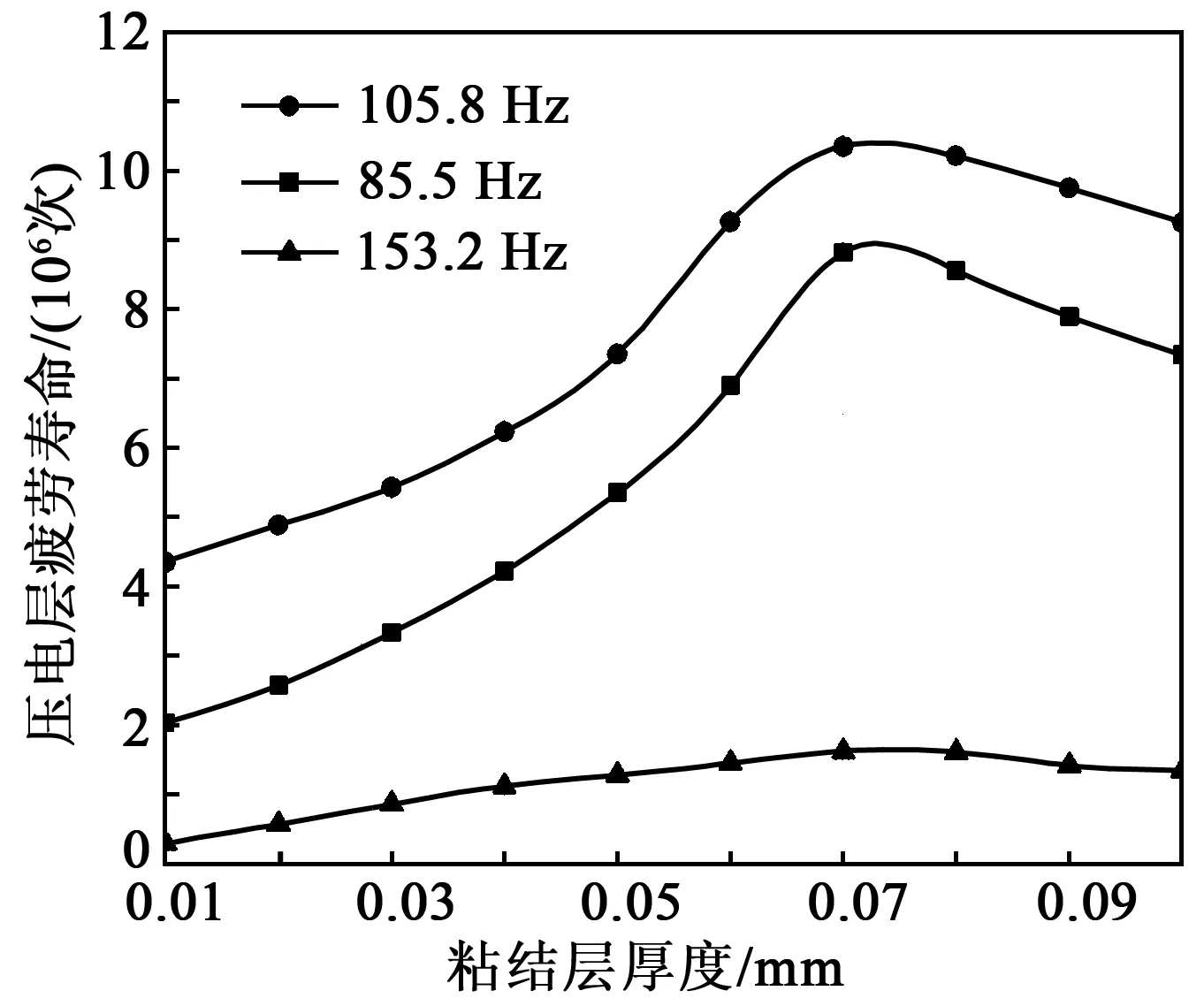
图7 压电层疲劳寿命与粘结层厚度的关系

4 结束语

本文对一种折叠式压电振子的疲劳寿命进行了分析。通过对粘结层的理论分析，在3种不同工作的模式下施加位移载荷，讨论了粘结层厚度对弹性层和压电层的应力变化情况，并将结果传输到疲劳分析软件中，得出折叠压电振子压电层的疲劳寿命分布云图。经过分析，当粘结层厚为0.07 mm时，在第2种工作模式下(105.8 Hz)压电层的疲劳寿命最高。

由此可见，粘结层厚度的变化和不同的位移载荷对压电陶瓷的疲劳寿命影响很大。在实际应用中，折叠压电振子应选择适宜的粘结层厚度和正确的工作模式，综合考虑压电陶瓷的疲劳寿命，才能实现最大的电能输出。