一种基于新的模糊距离测度的多属性决策方法
2020-10-28李逸飞林志超周礼刚
柏 杨,李逸飞,林志超,徐 鑫,周礼刚
(1.安徽大学 数学科学学院,合肥 230601; 2.安徽大学 计算机科学与技术学院,合肥 230601)
多属性群决策(MAGDM)问题是决策分析领域的重要研究方向,指对包含多个属性的有限备选方案,多个专家衡量备选方案的属性信息进行排序和选择的决策问题.然而随着科技进步和经济的不断发展,在实际生活中,决策信息日益复杂与模糊,以及决策者的主观性,决策者不能明确给出属性信息,往往选择以区间自然形式给出[1].距离测度是模糊集理论中度量不确定性信息的有效工具之一,衡量了信息之间的差异程度,在模糊识别、聚类分析、医疗诊断、图像处理和决策分析等多个领域得到广泛应用.
距离测度的构建主要利用加权平均手段,如加权平均汉明距离,加权平均欧式距离等[2].在有序加权距离测度中,Xu和Chen[2]首先提出了基于有序加权距离测度的群体共识达成法.Su和Li[3]研究了Atanassov的直觉语言有序加权平均距离测度及其在决策中的应用.Xian和Sun[4]研究了模糊语言诱导的欧式有序加权平均距离算子及其在群语言决策中的应用;Zeng和Su[5]给出了直觉模糊有序加权距离测度及其在金融决策中的应用;Zhou和Wu[6]等研究了语言连续有序加权距离测度及其在多属性群决策中的应用.随着模糊集理论的提出,在已有文献中,将距离测度应用于模糊集,丰富了模糊集应用的研究成果.
1965年,Zadeh[7]提出模糊集理论.1986年,Atanassov[8]提出了直觉模糊集,不仅考虑了隶属度,引入了非隶属度和犹豫度的概念,其中隶属度和非隶属度之和小于1.但客观世界还存在隶属度与非隶属度之和大于1的情况,Yager[9]将这种情况定义为Pythagorean模糊集,隶属度与非隶属度之和大于1,但隶属度与非隶属的平方和小于等于1,故其比直觉模糊集有更强的刻画客观世界模糊性的能力.Zhang与 Xu[10]给出了Pythagorean模糊集的TOPSIS方法.Zeng等[11]基于有序加权研究了Pythagorean模糊距离测度方法及其在多属性决策中的应用.Zeng和Mu[12]研究了基于混合加权视角的Pythagorean模糊距离测度的多属性决策方法.
虽然直觉模糊集和毕达哥拉斯模糊集已经处理实际决策问题的有用工具,但是他们评估信息的范围仍然有限.因此,为了克服这一限制,在原有理论的基础上,Yager[13]又提出了 Orthopair模糊集理论,其中隶属度的q次幂与非隶属度的q次幂之和等于1,此时直觉模糊集和毕达哥拉斯模糊集均为Orthopair模糊集的特例.这一理论的提出,引起诸多学者的广泛关注.Liu和Chen[14]研究了Orthopair模糊麦克劳林均值算子及其在多属性决策中的应用.Wei和Gao[15]研究了Orthopair模糊Heronian均值算子及其在多属性决策中的应用.
然而,在实际的决策问题中,由于决策者的主观性和决策环境的不确定性,决策者很难准确给出一个清晰的数字表达其观点,为了克服这一局限性,Wang和Gao[16]提出了区间Orthopair模糊集的定义,其中隶属度和非隶属度由一个区间值给出.Wang和Wei[17]研究了区间Orthopair模糊麦克劳林均值算子及其在多属性决策中的应用.
文献研究表明,Orthopair模糊集理论和应用的研究成果日趋丰富,但从有序加权平均视角研究区间Orthopair模糊距离测度方法比较少见,同时区间Orthopair模糊多属性决策方法也有待进一步完善.鉴于其在模糊识别、聚类分析、医疗诊断、图像处理和决策分析等问题上应用的重要性以及必要性.
1 预备知识
定义1[8]设X为论域,则称三元组
I={〈x,uI(x),vI(x)〉|x∈X}
(1)
为论域X上的直觉模糊集,其中:uI(x)和vI(x)分别为X中元素x属于I的隶属度和非隶属度,即uI(x):X→[0,1],vI(x):X→[0,1],且0≤uI(x)+vI(x)≤1.此外,X中元素x属于I的犹豫度πI(x)=1-[uI(x)+vI(x)],且0≤πI(x)≤1.
定义2[9]设X为论域,则称三元组
P={〈x,uP(x),vP(x)〉|x∈X}
(2)

定义3[13]设X为论域,则称三元组
Q={〈x,uQ(x),vQ(x)〉|x∈X}
(3)

定义4[16]设X为论域,则称三元组
A={〈x,uA(x),vA(x)〉|x∈X}
(4)
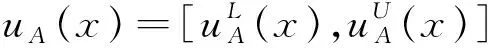
(5)
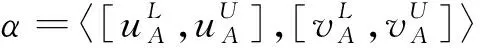

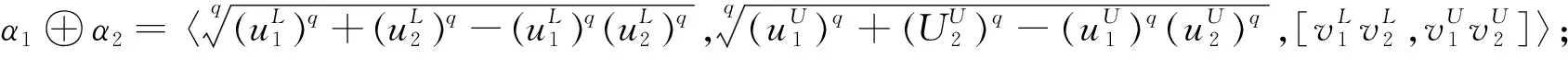
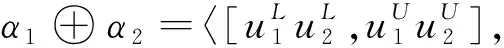
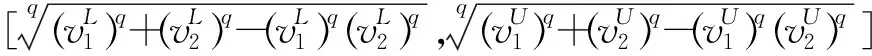

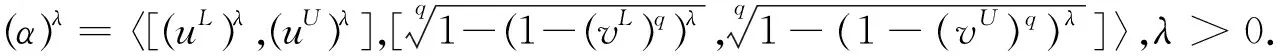
定义6α=<[uL,uU],[vL,vU]>设为一个区间Orthopair模糊数,称
(6)
为α的得分函数,
(7)
为α的精度函数.

1) 若S(α1) 2) 若S(α1)=S(α2),则若H(α1) (8) 为α1和α2的区间Orthopair模糊Hamming距离测度. 1)0≤d(α1,α2)≤1; 2)d(α1,α2)=d(α2,α1); 3)d(α1,α2)=0⟺α1=α2; 4)d(α1,α3)≤d(α1,α2)+d(α2,α3). (9) 显然,IOFWD测度仅考虑待集成指标的重要性,没有体现出其位置的重要.为此,提出区间Orthopair模糊有序加权距离(IOFOWD)测度. (10) 特别地,当λ=1和λ=2时,IOFOWD测度分别称为区间Orthopair模糊有序加权汉明距离(IOFOWHD)测度和区间Orthopair模糊有序加权欧式距离(IOFOWED)测度. (11) 为了确定权重ωj,本文运用正态分布函数给出IOFHWD测度的权重确定方法,即令 (12) 步骤1由式(13)计算专家权重L=(l1,l2,…,lt)T,其中 lk= (13) 步骤2由式(14)计算综合群决策矩阵R=(rij)m×n,其中 (14) 步骤3由式(15)、(16)分别计算区间Orthopair模糊正理想解r+和负理想解为r-: (15) (16) 步骤4由式(17)求解属性权重w=(w1,w2,…,wn)T,其中 (17) 其中 (18) (19) (20) 其中 (21) 步骤6由式(22)计算方案xi(i=1,2,…,m)的相对贴近度ξ(xi): (22) 相对贴近度ξ(xi)越大,说明方案xi越好. 步骤7根据方案的相对贴近度对方案进行排序,选出最优方案. “风险为本”的工作方法一直是反洗钱金融行动特别工作组所推崇的基本工作方法.准确评估金融机构和金融产品面临的洗钱风险,判断各类洗钱风险的大小程度,并依此形成对反洗钱工作资源的合理配置,完善洗钱风险控制手段,是实现有效控制洗钱风险,降低洗钱威胁的重要工作方法.为检验基于IOFHWD测度的TOPSIS多属性群决策方法在金融机构洗钱风险评估[18-19]中的可操作性和运用效果.现选取某地区4家银行x1,x2,x3,x4作为样本,依照上述多属性群决策方法,对这4家银行的洗钱风险状况进行评估.假设选取反洗钱监管部门2名人员,以及金融机构经验丰富的1名反洗钱从业人员,d1,d2,d3共同组成洗钱风险评估专家小组.根据以下四个主要指标属性来评估这四家银行:账户持有人身份识别风险(c1),账户使用人身份识别风险(c2),客户风险等级分类风险(c3),可疑交易报告风险(c4). 各个决策者给出的区间Orthopair模糊决策矩阵为R(k)=(k=1,2,3)如下: 步骤1 利用式(13)计算专家权重,得到L=(0.333 7,0.333 4,0.332 9)T,这里λ=3,q=3. 步骤2 利用公式(14),计算得到综合群决策矩阵:R=(rij)4×4 步骤3 利用公式(15)和(16)计算区间Orthopair模糊正负理想解r+和r-: r+=(〈[0.500 1,0.7293 ],[0.032 9,0.103 7]〉,〈[0.532 0,0.684 6],[0.078 1,0.111 7]〉,〈[0.444 4,0.635 4],[0.083 0,0.125 0]〉,〈[0.635 4,0.745 7],[0.032 9,0.084 1]〉) r-=(〈[0.227 4,0.415 7],[0.046 5,0.083 0]〉,〈[0.320 7,0.496 1],[0.086 3,0.138 8]〉,〈[0.350 4,0.549 4],[0.124 4,0.192 5]〉,〈[0.293 8,0.383 9],[0.061 5,0.131 7]〉) 步骤4 利用式(17)、(18)计算属性权重,得到w=(0.0226 3,0.318 5,0.241 0,0.214 3)T. 表1 各方案与正负理想解的混合加权距离 步骤6 利用式(22)计算各方案的相对贴近度ξ(xi),得到表2. 表2 各方案的相对贴近度 步骤7 排序择优. 根据表2可得,方案的相对贴近度排序为ξ(x4)>ξ(x2)>ξ(x1)>ξ(x3),即四家银行的风险排序为x4≻x2≻x1≻x3,x4银行的洗钱风险最高. 将本文的IOFHWD测度公式与IOFOWD测度公式进行比较,比较结果如表3.当λ=3,q=3,各方案与正负理想解的有序加权距离见表3. 表3 各方案与正负理想解的有序加权距离 基于以上有序加权距离,可得各方案的相对贴近度,见表4. 表4 各方案的相对贴近度 由表4可知,方案的相对贴近度排序为:ξ(x4)>ξ(x2)>ξ(x1)>ξ(x3),即四家银行的风险排序为x4≻x2≻x1≻x3,x4银行的洗钱风险最高,说明本文提到的方法是可行且有效的. 进一步分析IOFHWD测度中的参数λ和q的变化对相对贴近度函数和决策结果的影响.如图1所示,随着参数λ(q=3不变)的增加,方案x1,x2的相对贴近度单调减少,方案x3的相对贴近度先递减然后逐渐增加,方案x4一直是最优的;如图2所示,随着参数q(λ=3不变)的增加,各方案的相对贴近度均单调减少,排序结果也随之变化,但方案x4一直是最优的.根据IOFHWD中的参数特征发现,λ的大小可用于体现决策者决策风险偏好的程度. 图1 各方案的相对贴近度函数(基于λ) 由分析可知,本文提出的基于IOFHWD测度的多属性群决策方法具备良好性质.相比较麦克劳林对称平均算子[17]直接给出权重,本文利用混合加权平均距离测度计算权重的方法,不仅考虑了数据的重要性,而且突出了数据所在位置的重要性,从而可以增大或降低偏差过大或者过小数据决策结果的影响.同时提出的区间Orthopair模糊集有更好的刻画模糊的能力,其适用范围也更广泛. 图2 各方案的相对贴近度函数(基于q) 本文从有序加权视角研究了基于区间Orthopair模糊混合加权距离(IOFHWD)测度的TOPSIS多属性群决策方法及其应用.定义了区间Orthopair模糊有序加权距离(IOFOWD)测度,考虑不同的属性权重信息情况,有效消除了过大或过小的不合理信息造成的误差.在IOFOWD测度的基础上,进一步提出了区间Orthopair模糊混合加权距离(IOFHWD)测度,考虑数据本身数据的重要性,体现数据所在位置的重要程度.提出一种基于IOFHWD测度的TOPSIS多属性群决策方法,利用IOFHWD测量方案与正负理想解的距离,计算得到方案的相对贴近度,并根据其大小对方案进行排序择优.案例说明了新方法的可行性和有效性.2 区间Orthopair模糊混合加权距离测度

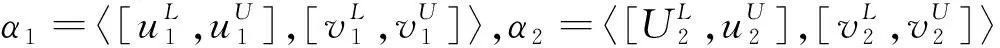



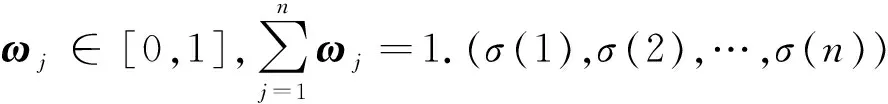

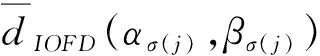
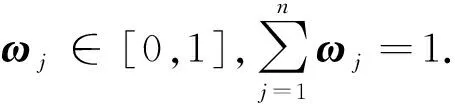
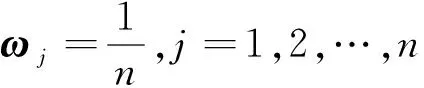
3 基于IOFHWD测度的TOPSIS多属性群决策方法

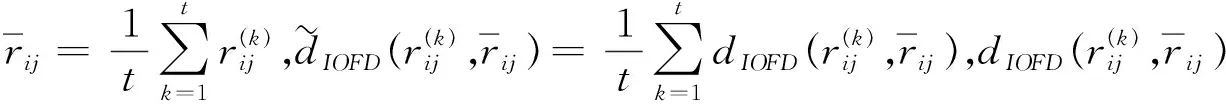


4 实例分析

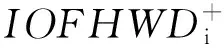






5 结 语
